Feedback Stabilization for a Scalar Conservation Law with PID Boundary Control∗

Jean Michel CORON Simona Oana TAMASOIU

(Dedicated to Luc Tartar with the Souvenir of His Wonderful Course at Ecole Plytechnique)

1 Introduction

Within process control,one of the most widely used controller type is the proportionalintegral-derivative(PID for short)controller(see,e.g.,[1,17]and the references therein).The main idea of a PID controller is that the system state is steered to a given desired equilibrium based on information about the present error(a proportional controller gain,or kpbelow),the accumulated past error(an integral control term,ki)and also on the estimation on future error(a derivative controller gain,kdterm).

In this paper,we address the stability analysis for a scalar conservation law in 1-D space dimension,subject to PID boundary control.In particular,we analyze the stability of the constant equilibrium solution,under such a PID boundary controller.More precisely,we are concerned with designing appropriately the control feedback parameters in such a way that the solutions to certain Cauchy problems converge(exponentially fast)to a desired steady solution(or equilibrium),where by equilibrium,we understand a constant solution that verifies the state equation and constant boundary control.

For the asymptotic stability of hyperbolic systems,two main approaches were used in the corresponding literature:The method of characteristics and Lyapunov function techniques.As for the first strategy,we mention[10]and[12,Chapter 5]where the authors proved asymptotic stability for quasilinear hyperbolic systems by analyzing the solution along the characteristic curves.This method can also be used to study robustness issues,as shown in[15].The second strategy,by a Lyapunov function approach,permits direct extension of the stability results from linear to nonlinear systems.This is an important fact that since a small perturbation in the constant velocity can induce instability,we can not directly deduce stability for the nonlinear system from the stability of its linearization.For a system of 2 conservation laws with a proportional feedback controller,we refer to[6],where the authors analyzed the stability of constant equilibrium for the linear and nonlinear systems,by Lyapunov function approach.Another related work,where Lyapunov techniques were used,is[9],where the authors discussed exponential stability for the linear 2×2 system case under proportional and integral(PI for short)boundary control.For Lyapunov stability of nonconstant equilibrium with application to isothermal Euler equations,we refer to[8],where stability in L2-norm for a sequence of pipes was proved.For the general case of n×n nonlinear hyperbolic systems,we mention[5].In[2],the authors analyzed the stability of non-uniform linear hyperbolic systems and they showed how the existence of a control Lyapunov function is related to the fact that the solution of a linear ODE is defined on the considered space interval.

The aim of this paper is the stability analysis of the following scalar conservation law:

where r(t,x)denotes the system state over the space interval(0,L),L>0 and time domain[0,+∞).Here,>0 denotes the velocity of the system state,and it is assumed thatis constant.

Together with(1.1)we consider boundary condition in the following feedback form(t∈[0,∞)):

with kp,kiand kdbeing feedback parameters representing a proportional,integral and derivative control gain,respectively.In particular,when we speak about PI control,kdis set to zero in(1.2),i.e.,the controller scheme is of the type

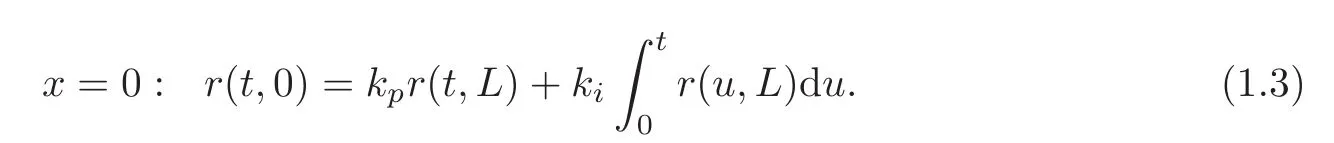
A similar problem is treated in[7],where the authors studied the output feedback stabilization for a scalar conservation law with a nonlocal velocity,an equation that models the semiconductor manufacturing systems.However,in[7],the boundary condition has a different form to that in our case.By spectral analysis,the authors characterized the stabilizing set of feedback parameters for the linearized equation.The analysis is based on degree theory for homotopic functions(see[4,Appendix B]).

The contribution of our paper is twofold:First,we study the exponential stability of(1.1)under proportional-integral(PI for short)control:We give necessary and sufficient conditions on the feedback parameters kpand kiin such a way that the closed-loop system(1.1)and(1.3)is exponentially stable.Also,the time delay stability interval is given.Furthermore,we discuss stability for the classical PI controller by Lyapunov function techniques,and by the same approach,we prove exponential stability for the closed-loop system when a damping term is added to the PI controller scheme.Second,we show that the plant with the dynamics given by(1.1)cannot be stabilized by the PID controller(1.2).As we shall see,this follows directly from a result by Pontryagin,on stability of quasipolynomials.

The structure of the paper is as follows.The precise problem formulation and the main results are given in Section 2.In Section 3,we recall the Walton-Marshall stability criterion.Based on the aforementioned criterion,in the first part of Section 4,we give the proof of the main results.In the second part of Section 4,we make several notes regarding the Lyapunov function approach for the PI control system and we also prove,by Lyapunov techniques,exponential stability for the closed-loop system when a damping term is added to the PI controller scheme.In Section 5,the case of stabilization under the PID boundary controller is treated.Finally,several concluding remarks are given by the end of this paper.

2 Problem Formulation and Main Results

Within the stability analysis,it is important to mention that the time delay of a system plays a key role,as it can induce instability,or on the contrary,it can have a stabilizing effect.This problem was extensively studied(see,e.g.,[1]).A notion about how increasing delay inf l uences stability can be found in[3].The authors discussed stability of solutions of scalar differential-difference equations with a single delay.The notion of strong exponential stability,i.e.,stability under small variations in time delay,was introduced in[11],and in this context,necessary and sufficient conditions for existence of a feedback control were given.

In our case,for the dynamics given by(1.1),the time delay is constant,and we denote it by τ which is given by

The closed-loop characteristic equation under PI control is,after a multiplication byµ,

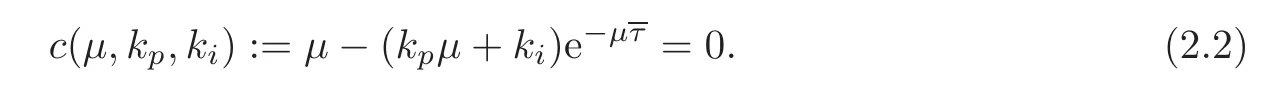
Analogously,the closed-loop characteristic equation under the PID controller is equivalent to

The stability of the closed-loop systems(1.1)–(1.3)and(1.1)–(1.2)reduces to determining the location of the zeros of(2.2)–(2.3),respectively.We are now able to give a more precise formulation of the problem that we are concerned with in this paper.This has two parts,formulated as follows.

Derive conditions on the feedback parameters kp,kiand obtain the time delay interval for which the closed-loop system under the PI feedback control law(1.3)is exponentially stable.Analyze stability under the PID boundary feedback control(1.2).

In the sequel,L2(0,L)denotes the Lebesgue space of square integrable functions f:[0,L]→R,equipped with the usual L2-norm on[0,L]as follows:

Our main results are given in the following theorems.The first theorem is about stability with a PI controller.For ki6=0 and kp∈ (−1,1),let us define τ0∈ (0,+∞)by

Theorem 2.1Let us assume that ki6=0.The closed-loop system(1.1)and(1.3)is exponentially stable for the L2-norm if and only if the feedback parameters kp,kisatisfy|kp|<1,ki<0 and the time-delayis such that∈ (0,τ0).

The next result is about the corresponding PID controller case.

Theorem 2.2Let us assume that kd6=0.The characteristic equation(2.3)has infinitely many zeros with arbitrarily large positive real parts.In particular,the closed-loop system(1.1)–(1.2)is always unstable.

3 Walton-Marshall Stability Criterion for Time-Delay Systems with Single Delay

In this section,we prove Theorem 2.1 by spectral analysis,and we obtain a complete characterization of the set of stabilizing feedback parameters kpand ki,as well as the time delay stability interval.

Let us first recall that,in infinite dimension,the fact that all the eigenvalues of an unbounded linear operator A lie in the complex half plane{z ∈ C;ℜ(z)≤ −δ}for some δ>0 is not a sufficient condition for the exponential stability of=Ay.A counterexample dealing with linear hyperbolic systems of PDEs in dimension 2 was constructed in[16].However,by using the results in[13],the above phenomena does not hold for the closed systems considered in this paper:For our closed loop systems,the exponential stability is equivalent to the existence of δ>0 such that all the zeroes of the characteristic equation are included in the complex half plane.Based on this fact,there is a significant number of criteria/works which can be used,such as the Ziegler-Nichols method,optimization methods,analytical tuning methods,etc.(for a more complete exposition,we refer to[1]).We start by recalling such a stability criterion.Afterwards,we exemplify the algorithm in the case of P-controller and we conclude the section with the proof of Theorem 2.1.We recall a stability criterion for time delay systems with a single delay,which is due to Walton and Marshall in 1987(see[17–18]and the references therein).Time delay systems with a single delay have a characteristic equation of the following form:

where by µ ∈ C,we denote the eigenvalues of the system,and f(µ),g(µ)are polynomials with real coefficients,such that deg[f(µ)]=p,deg[g(µ)]=q.It is moreover assumed that f and g are coprime polynomials and that p≥q.

The Walton-Marshall stability criterion consists in three steps,as outlined below.For a more detailed description,we refer to[17,Subsection 5.6]and[18].

Step 1In this step,we analyze stability in the case free of delay,i.e.,when τ=0.

Step 2In the second step,we increase the time delay τ from zero to a strictly positive τ>0,and in this context,we evaluate how the eigenvalues move with increasing τ.The analysis is divided into two cases,according to the degrees of f(µ)and g(µ),i.e.,p and q,respectively,as follows.

If p>q,all the new zeros of the characteristic equation are in the left half plane and this step can be omitted.If,however,p=q,we analyze potential crossings of the imaginary axis,i.e.,we consider purely imaginary eigenvaluesµ =iω,ω ∈ R.

By using the properties of the conjugate of a complex number,we note that ifµ =iω,ω ∈ R is a solution of c(µ)=0,then −µ = −iω,ω ∈ R is also a solution.By replacing ±iω in(3.1)and eliminating the exponentials,we obtain a real polynomial in ω2,which we denote by P(and which is)given by

A necessary condition for exponential stability is that

holds.

Step 3In a third and final step,we determine the positive roots of P,the corresponding time delay,and also whether these roots are stabilizing or destabilizing as τ is increasing.We are thus interested in the positive real solutions y:=ω2of the equation

with P defined in(3.2),as they can lead to crossing the imaginary axis,and therefore to a change in the stability.

Remark 3.1We note that if(3.4)has no positive real roots,then there is no change in stability:If the system is stable(unstable)in the case free of delays τ=0,then the system is stable(unstable)for all delay values τ>0(see[17,Subsection 5.6,Remark 5.2]).

If this is not the case,we determine the positive roots y:=ω2>0 of(3.4).For positive roots y= ω2>0,by using the characteristic equation f(iω)+g(iω)e−iωτ=0,the time delay τ satisfies,if g(iω)6=0,

Once we have found a value of τ such that c(µ)has a root on the imaginary axis,we analyze the behaviour of this root with respect to changes in τ.More precisely,we analyze whether,as τ is increasing,this root crosses the imaginary axis from the right half plane into the left half plane(a stabilizing root),or vice versa,if it goes from the left half plane into the right half plane(a destabilizing root).

It was shown in[18](see also[17,Subsection 5.6])that a nonnegative root y≥0 of P is stabilizing if P′(y)<0 and destabilizing if P′(y)>0.Here,the prime denotes the first derivative with respect to y.If the derivative P′(y)is zero,one considers higher-order derivatives.

In what follows,we give an example of application of Walton-Marshall stability criterion,in the case of proportional(P for short)feedback control.This result is well established in the corresponding literature.For a proof using Lyapunov function techniques,we refer to[6],where necessary and sufficient stability conditions were derived for the 2×2 system case,and to[5],where the authors proved stability for general n×n nonlinear hyperbolic systems.Afterwards,we complete the proof of Theorem 2.1.

Example 3.1We assume that ki=kd=0 in(1.3),i.e.,the P-boundary controller is(t∈ [0,∞))

In this case,the characteristic equation of(1.1),(3.6)is

where as above we denote byµ∈C the eigenvalues of(1.1)with the boundary condition(3.6),and as above,denotes the time delay.We want to apply the Walton-Marshall criterion described in Section 2,and thus we identify

In particular,for µ =iω,ω ∈ R,

First,we analyze the stability in the case free of delays,i.e.,τ=0 and afterwards,as p=q=0,the location of the new eigenvalues with increasing τ is determined by the sign of P(ω2)for large ω∈R.

Step 1If τ=0,c1(µ)becomes c1(µ)=1 − kp.

Step 2The polynomial P(ω2)in(3.2)is in this case given by(3.9),and we note that it does not depend on ω2,so Step 3 is not required here.

In conclusion,the necessary and sufficient condition for exponential stability is given by the positivity of P,for large ω ∈R,i.e.,1−k2p>0,or equivalently,|kp|<1.

We make the following remark,concerning the influence of the time delay τ in the stability analysis.

Remark 3.2We observe that in the proportional controller case,the necessary and sufficient stability condition is independent of the time delay,i.e.,the closed-loop system(1.1)and(3.6)is exponentially stable if and only if|kp|<1,for arbitrary value of time delay τ.

As we shall see later on,this is not the case for a proportional-integral controller,where the stability condition involves the time delay as well,as already announced in Theorem 2.1.

4 Stabilization with PI controller

4.1 Proof of stability under the classical PI controller by spectral analysis

In this section,we assume that ki6=0,and prove Theorem 2.1.As mentioned above,the characteristic equation of(1.1)and(1.3)is

with the same notations as before.We identify

In particular,forµ =iω,ω ∈ R,

As for Example 3.1,let us now analyze the three steps of the stability criterion,starting by examining the delay free system.

Step 1If=0,c2(µ)=0 is,by(2.2),equivalent to

Thus,the zero delay system is exponentially stable if and only if one of the following two inequalities:

holds.

Step 2Letµ =iω,ω ∈ R.As p=q=1(in(4.2)),we remark that a necessary condition for exponential stability is that(3.3)holds.From(4.3),we get that(3.3)holds if and only if

Until the end of Subsection 4.1,we assume that(4.6)holds.Furthermore,in the view of(4.5),we obtain that

has to be satisfied in order to have exponential stability.From now on,we assume that(4.7)holds.

Step 3In this step,we analyze potential crossings of the imaginary axis.We are interested in the positive roots y:=ω2of P(y)=0,as they can lead to crossing of the imaginary axis,and thus to change in stability.

We analyze the roots of(4.3).We consider the nonegative rootof(4.3),given by

Asthis root is destabilizing.The corresponding time delay valuesatisfies

The smallest>0 such that(4.9)holds is τ0defined in(2.4).It means that at τ0,a first pair of eigenvalues(µ = ±iω0)crosses from the region of stability(left half of the complex plane)into the region of instability(right half of the complex plane)and there is no stabilizing effect,so the roots will accumulate in the right half plane.This concludes the proof of Theorem 2.1 by means of spectral analysis.

4.2 A note on Lyapunov function approach

Based on the previous considerations in the corresponding literature,we might have expected that a function of the type

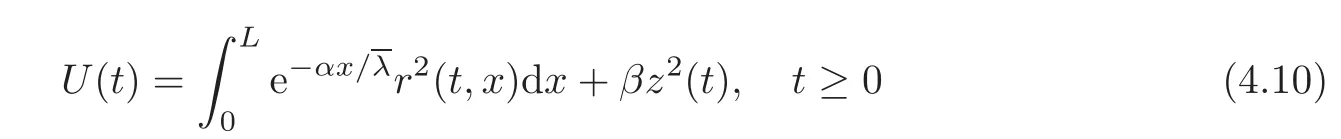
is a Lyapunov function for the closed loop system(1.1)and(1.3).However,in this section,we shall show that this is not the case here.

Theorem 4.1Assume that ki6=0.Then there exist no β >0 and α such that U defined by(4.10)is a Lyapunov function for the closed-loop system(1.1)and(1.3).

ProofBy taking the time derivative of U(t)along the trajectories of(1.1)and(1.3),we obtain,with a simple integration by parts,

where

In order to insure that U is coercive(in L2(0,L)×R),one must have

In order to have≤0 whatever the trajectory of the closed loop system(1.1)and(1.3)is,one must have

which does not hold.

Remark 4.1In fact,by following the same procedure,it can be proved that any function of the type

with g∈C1([0,L])is not a Lyapunov function for(1.1)and(1.3).Let us consider an even more general Lyapunov function candidate of the type

with gi,i∈{1,2,3}of class C1.According to[2,Proposition 3],we obtain that the coefficient of the mixed term is zero,i.e.,g3=0,for any x∈[0,L].Hence,as V,cannot be a Lyapunov function for(1.1)and(1.3).

4.3 PI controller with damping

In this section,we show that if a damping term is added to the controller scheme(see(4.18),and in particular,the term klz),the function U defined by(4.10)can indeed be a Lyapunov function for the closed-loop system.More precisely,we consider the following boundary feedback controller:

We note that the classical PI controller case,treated in the previous sections,corresponds to the case kl=0 and kj=1.Throughout this section,we assume

The characteristic equation of the system(1.1)and(4.17)–(4.18)is

In the free of delay case,the characteristic equation reduces to

Also,the polynomial P(ω2)is

with the same notations as before.Applying the Walton-Marshall stability criterion(and looking at the large solutions of(4.20)in the “degenerate” case|kp|=1)one gets the following theorem.

Theorem 4.2If the system(1.1)and(4.17)–(4.18)is exponentially stable,then

If(4.23)–(4.24)hold and

then,for every>0,the system(1.1)and(4.17)–(4.18)is exponentially stable.If(4.23)–(4.24)hold and

then the system(1.1)and(4.17)–(4.18)is exponentially stable if and only if∈ (0,τ1),whereis the smallestsuch that

with

Remark 4.2Let us point out that(4.24)–(4.25)imply that kl<0,from which the name of the controller(with damping)comes.

Let us now recover the exponential stability in the case where(4.23)–(4.25)hold by means of a Lyapunov approach.

Theorem 4.3Let us assume that(4.23)–(4.25)hold.Then there exist α >0, β >0 and θ>0 such that,along the solution r(t,x),z(t)of the closed-loop system(1.1)and(4.17)–(4.18),

where U is defined in(4.10).

ProofThe proof is similar to that of Theorem 4.1.By taking the time derivative of U along the trajectories of the closed-loop system(1.1),we obtain

where

By using(4.17)–(4.18),we equivalently rewrite(4.31)as

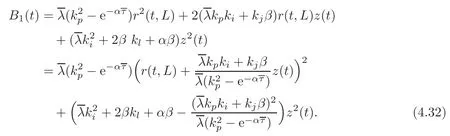
It now suffices to check that there exist α >0 and β >0 such that B1(t),considered as a quadratic form in the variables r(t,L)and z(t),is negative definite.We first consider the case α=0.Then,by(4.23),B1(t)is negative definite if and only if

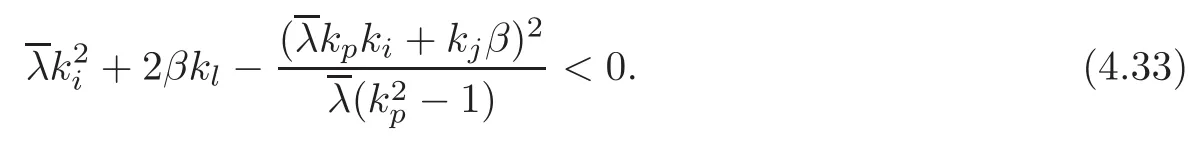
Taking into account(4.23),inequality(4.33)is equivalent to

an inequality with a second-order polynomial in β.Our task now is to show that there exists β >0 such that(4.34)holds.First,we note that(4.23)–(4.25)imply that

which,together with(4.34),means that the sum of the roots of F is strictly positive.The discriminant of F is

which,together with(4.23)–(4.25),implies that ∆F>0.Hence the two roots of F are real and distinct.Moreover,using(4.35)and the fact thatone gets that one of the roots is positive and the other one is nonnegative.Hence there exists β>0 such that B1(t)is a negative definite quadratic form.By a simple continuity argument with respect to α,we obtain that there exist α >0 and β >0 such that(4.31)is a negative definite quadratic form.This fact,together with(4.30),concludes the proof of Theorem 4.3.

5 Stabilization with PID Controller

In this section,we consider the case of PID(proportional,integral and derivative)controller,and we show that a plant with the dynamics(1.1)cannot be stabilized with such a PID controller.The analysis is based on a version of Pontryagin’s theorem for stability of quasipolynomials(i.e.,polynomials involving exponential terms).The result given by Pontryagin in[14]is one of the first and most fundamental stability criteria,and it is widely used in engineering and control theory.Pontryagin gave necessary and sufficient stability conditions for quasipolynomials in two variables with real or complex coefficients of the following form:

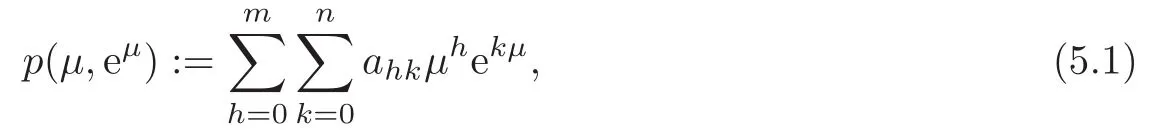
where

(1)there exists k ∈ {0,···,n},such that amk6=0,

(2)there exists h ∈ {0,···,m},such that ahn6=0.

Definition 5.1The quasipolynomial p(µ,eµ)is said to have a principal term if

i.e.,there exists a nonzero coefficient ahkwhere both indices h and k have maximal values.

In this context,we recall the following stability result,due to Pontryagin[14],given in[17,Theorem 5.1].

Theorem 5.1(see[14])If the polynomial p(µ,eµ)as in(5.1)does not have a principal term,then the the equation P(µ):=p(µ,eµ)=0 has an infinite number of roots with arbitrarily large positive real parts.

We now return to the case of the PID controller,and we show that the closed loop system(1.1)together with the PID boundary controller

is unstable.This is a direct application of Theorem 5.1.The corresponding characteristic equation of the PID controller is

Let us perform the change of variables ν :=µ.Then c(µ)=0 is equivalent to q(ν)=0 with

According to Definition 5.1,the quasipolynomial q(ν)does not have a principal term.Theorem 5.1 implies that c(µ)admits infinitely many rootsµ ∈ C with arbitrarily large positive real parts,so the closed-loop system(1.1)and(1.3)is unstable.This concludes the proof of Theorem 2.2.

6 Conclusion and Perspectives

In this paper,we deal with a scalar conservation law in 1-D space dimension.Precisely speaking,we derive necessary and sufficient conditions for exponential stability of the closedloop system under PI(with and without damping)boundary control.Moreover,we show that the feedback system under PID control is always unstable.

An interesting open problem would be to recover,by means of the Lyapunov function,Theorem 2.1 in order to treat the nonlinear case and handle quantitative robustness issues.Another open problem is to deal with systems of n>1 conservation or balance laws.

[1]Åström,K.J.and Hägglund,T.,PID Controllers:Theory,Design,and Tunning,Instrument Society of America,Research Triangle Park,NC,1995.

[2]Bastin,G.and Coron,J.M.,On boundary feedback stabilization of non-uniform linear 2×2 hyperbolic systems over a bounded interval,Systems Control Lett.,60(11),2011,900–906.

[3]Cooke,K.L.and Van den Driessche,P.,On zeroes of some transcendental equations,Funkcial Ekvac.,29(1),1986,77–90.

[4]Coron,J.M.,Control and nonlinearity,Mathematical Surveys and Monographs,Vol.136,AMS,Providence,RI,2007.

[5]Coron,J.M.,Bastin,G.and d’Andréa-Novel,B.,Dissipative boundary conditions for one-dimensional nonlinear hyperbolic systems,SIAM J.Control Optim.,47(3),2008,1460–1498.

[6]Coron,J.M.,d’Andréa-Novel,B.and Bastin,G.,A strict Lyapunov function for boundary control of hyperbolic systems of conservation laws,IEEE Trans.Automat.Control,52(1),2007,2–11.

[7]Coron,J.M.and Wang,Z.Q.,Output feedback stabilization for a scalar conservation law with a nonlocal velocity,SIAM J.Math.Anal.,45(5),2013,2646–2665.

[8]Dick,M.,Gugat,M.and Leugering,G.,Classical solutions and feedback stabilization for the gas flow in a sequence of pipes,Netw.Heterog.Media,5(4),2010,691–709.

[9]Dos Santos,V.,Bastin,G.,Coron,J.M.and d’Andréa-Novel,B.,Boundary control with integral action for hyperbolic systems of conservation laws:Stability and experiments,Automatica J.IFAC,44(5),2008,1310–1318.

[10]Greenberg,J.and Li,T.T.,The effect of boundary damping for the quasilinear wave equation,J.Differential Equations,52(1),1984,66–75.

[11]Hale,J.K.and Verduyn Lunel,S.M.,Strong stabilization of neutral functional differential equations,IMA Journal of Mathematical Control and Information,19,2002,5–23.

[12]Li,T.T.,Global classical solutions for quasilinear hyperbolic systems,Research in Applied Mathematics,Vol.32,Masson,Paris,1994.

[13]Lichtner,M.,Spectral mapping theorem for linear hyperbolic systems,Proc.Amer.Math.Soc.,136(6),2008,2091–2101.

[14]Pontryagin,Lev Semionovitch,On the zeros of some elementary transcendental functions,Amer.Math.Soc.Transl.(2),1,1955,95–110.

[15]Prieur,C.,Winkin,J.and Bastin,G.,Robust boundary control of systems of conservation laws,Math.Control Signals Systems,20(2),2008,173–197.

[16]Renardy,M.,On the linear stability of hyperbolic PDEs and viscoelastic flows,Z.Angew.Math.Phys.,45(6),1994,854–865.

[17]Silva,G.J.and Datta,A.and Bhattacharyya,S.P.,PID controllers for time-delay systems,Control Engineering,Birkhäuser,Boston,2005.

[18]Walton,K.and Marshall,J.E.,Direct method for TDS stability analysis,Proceedings of IEEE,134(D),1987,101–107.