Long-Time Turbulence Model Deduced from the Navier-Stokes Equations∗

Roger LEWANDOWSKI

(In Honor of the Scientific Contributions of Professor Luc Tartar)

1 Introduction

This paper aims to report results that have been exposed during a talk given at the“International Conference on Nonlinear and Multiscale Partial Differential Equations:Theory,Numerics and Applications,Fudan University,Shanghai” in China September 16–20,2013 in honor of Luc Tartar.These results were first obtained in[5].

Turbulent flows are chaotic systems,highly sensitive to small changes in data(see[15]),which means that any tiny change in body forces,any external action and/or initial data,might give rise almost instantly to significant changes in the flow features.

To be more specific,let us consider an experiment which measures the velocity(or one of its components)of a turbulent flow N times at a given point.Each measurement is carried out under the same conditions(the same initial data,constant temperature,and the same source).Although advanced technologies allow measurements to be made to high precision,the experiment will yield N different results,because in reality infinitesimal changes occur during each measurement that cannot be controlled.

Moreover,because of the structure of the turbulence,any code using the Navier-Stokes equations(NSE for short)

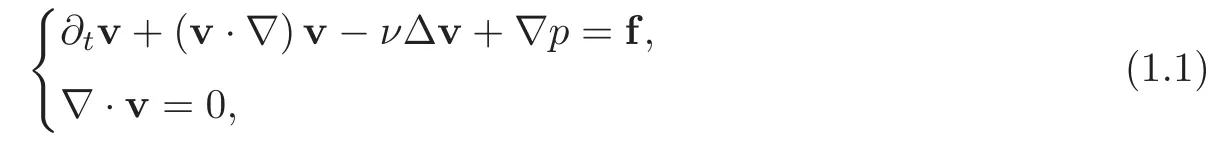
that specify flow motions(see[2,5]),would be very complex and would require too many computational resources in order to run the simulation.In the equations above,v=(v1,v2,v3)=v(t,x)denotes the Eulerian velocity of the fluid,p=p(t,x)denotes its pressure,(t,x)∈R+×Ωfor some bounded domain Ω ⊂ R3,ν >0 is the kinematic viscosity and f is a given external force.Throughout this paper,we assume that v satisfies the no slip boundary condition,i.e.,v|Γ=0,and that v0=v0(x)=v(0,x)is a given initial data.

A long time ago,Reynolds[14],Stokes[17],Boussinesq[3]and Prandtl[13]suggested to decompose the flow field as the sum of a mean field and a fluctuation,i.e.,

In those works,the meansandwere formally expressed by long time averages

Later,Taylor[20]and then Kolmogorov[7]considered statiscal means instead of long-time averages(see details also in[5]).

We focus in this paper on the long-time average(1.3),and in particular:

(i)We show that the long-time averageis well-defined in some Sobolev spaces for global turbulent solutions of the NSE(1.1),when the domain Ω is smooth enough,and under appropriate assumptions on the source term f and the initial data v0.

(ii)We show thatsatisfy the steady-state NSE,with an additional source term of the form −∇σ(R),where σ(R)is a Reynolds stress.Finally,We show that σ(R)is dissipative.

We mention that recently Layton[10]showed that,for smooth solutions of the NSE that satisfy the energy equality,the Reynolds stress is also dissipative when considering ensemble averages.

This paper is organised as follows.Section 2 is devoted to outlining the functional framework which we shall use,to recalling the basic Leray-Hopf result(see[6,11])that states the existence of turbulent solutions of the NSE,and to deriving from the energy inequality long-time estimates.We then proceed with the programme set out above in Section 3.

2 Framework and Basic Results

2.1 Functional spaces

We assume in this section that Γ is of class C1for simplicity.1Many results reported in this section also hold for Lipchitz domains(see for instance[18]).For given q,p,s,we set

We denote by k ·kq,p,Ωthe standard Ws,p(Ω)norm.For anywe consider the spaces

In the above definition,γ0is the trace operator,which is defined by

that can be extended to Hs(Ω),whenin a continuous operator with values in the spaceWhen no risk of confusion occurs,we also denote γ0w=w.The spaceis equipped with its standard norm

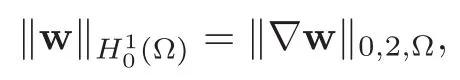
which is a norm equivalent to the k ·k1,2,Ωnorm,due to the Poincaré’s inequality.Details about Sobolev spaces can be found in[19].We shall also make use of the following spaces:

In the definition above,γnis the normal trace operator,which is defined by

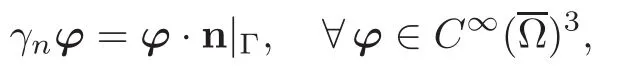
the vector n being the outward-pointing unit normal vector to Γ.We know that this operator can be extended toin a continuous operator with values in the space(see[8]),where

2.2 Variational formulation of the NSE

For simplicity,we denote by(u,v)the duality pairing hLp′(Ω),Lp(Ω)i,

and we define the diffusion and transport operators by

respectively.We know that these multilinear forms are continuous over H1(Ω)(see[5]).Moreover,we also know that,∀z,v ∈ Vdiv(Ω),∀p∈ L2(Ω),

We assume from now on that

Following[6,11],we say that v is a turbulent solution of the NSE(1.1)if and only if∀T>0,

and∀w∈Vdiv(Ω),

Remark 2.1According to the definition of the space Lp([0,T],E)through the Bochner integral,where E is any given Banach space(see[16]),(2.12)can be replaced by

(see[5]for instance).

The following existence result is standard(see[6,11]).

Theorem 2.1The NSE(1.1)has a turbulent solution which satisfies the energy inequality at every t∈[0,T],i.e.,

The uniqueness of this solution is still an open problem at the time of writing this paper.Similarly,we do not know if the energy inequality(2.15)is an equality.The energy inequality(2.15)also yields

for all t>0.The pressure is recovered from the De Rham’s theorem,leading to the following statement(see for instance[9,12,18,21]).

Lemma 2.1There existssuch that(v,p)is a solution of the NSE(1.1)in the sense of distributions.

In the statement above,

The pressure p is considered as a constraint in this kind of formulation.Therefore,p is called a Lagrange multiplier.It can also be proved that(see for instance[4]).

2.3 Long-time estimate

From now on and until the end of the report,we assume that the source term f∈ H−1(Ω)⊂Vdiv(Ω)′does not depend on t,and we set F=kfk−1,2,Ω.

The real number µ denotes the best constant in the Poincaré’s inequality,written as

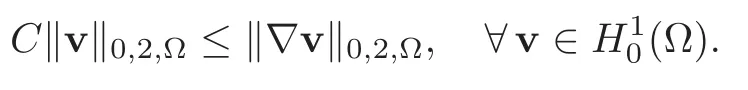
The energy inequality(2.16)yields that kv(t,·)k0,2,Ωis bounded uniformly in t.To be more specific,we prove the following proposition.

Proposition 2.1Let v be any turbulent solution to the NSE.Then we have

for all t>0.

ProofSet

Energy inequality(2.15)yields

We apply Poincaré’s inequality in the second term of the left-hand side of(2.19),leading to

Therefore,W is a subsolution of the ordinary differential equation

the solution of which is

and hence(2.17)holds.

As a consequence,we deduce that the turbulent solution is well-defined all over R+,and hence can be extended toas a global time solution.In particular,we have

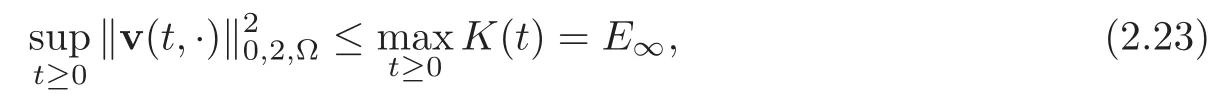
where

We also deduce from(2.19)combined with(2.23),the following inequality:

Moreover,from standard interpolation inequalites(see[5]),we infer that

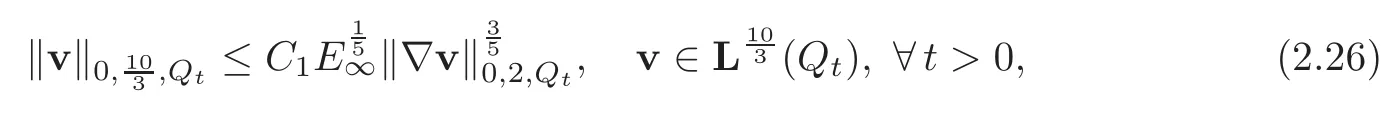
leading to

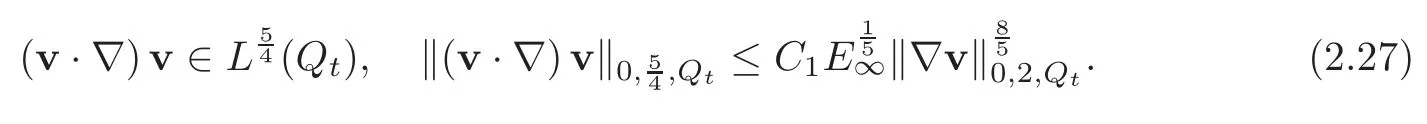
3 Main Results

3.1 Long-time average operator

We start with the study of the mean operator Mtover[0,t],for a given fixed time t>0,expressed by

ψ=ψ(t,x)being any given field.

Lemma 3.1Let t>0,Qt=[0,t]× Ω.Assume ψ ∈ Lp(Qt).Then Mt(ψ) ∈ Lp(Ω)and one has

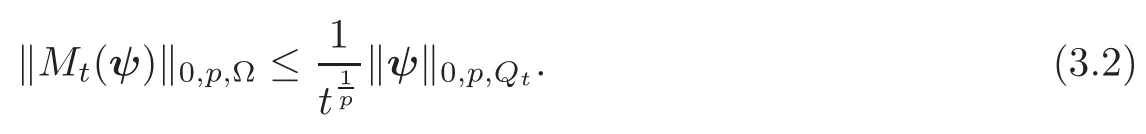
Proof By the Hölder’s inequality,we have

Thus(3.2)follows by Fubini’s theorem.

We study the effect of Mton(v,p)in defining

We deduce from the NSE that(Vt,Pt)is the solution of the following Stokes problem,at least in the sense of distributions,

In(3.5),

which goes to zero in L2(Ω)when t→ +∞,according to(2.23).

3.2 Existence of velocity-pressure long-time averages

In addition to the previous assumptions,we assume now that the domain Ω is of classanddoes not depend on t,

Theorem 3.1There exists

(i)a sequence(tn)n∈Nthat goes to+∞ when n→+∞,

(ii)

(iii)

such that(Vtn,Ptn)n∈Nconverges toweakly inthat satisfies

in the sense of distributions.

ProofThe proof is divided into 3 steps.We first find estimates and extract convergent subsequences.We then take the limit in the equations,firstly in the conservation equation,and then in the momentum equation.

Step 1We first show that the nonlinear term −Mt((v·∇)v)is bounded inBy(3.2),we have

where Qt=[0,t]×Ω.Combining this inequality with(2.23)and(2.27),we find

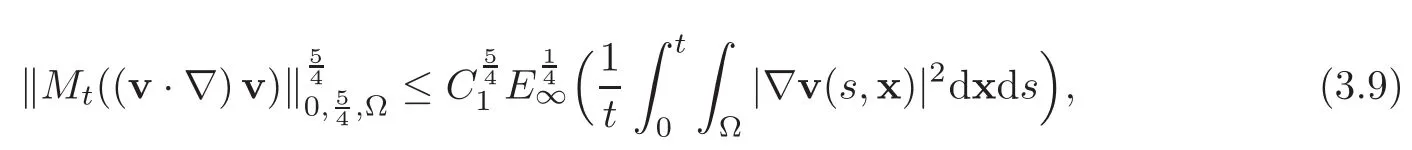
and hence(Mt((v·∇)v))t>0is bounded inuniformly in t due to(2.25).Since Ω is of classand

the results in[1]apply,that is,there exists a unique solution(Vt,Pt)of(3.5)that satisfies

Because of uniqueness,this solution(Vt,Pt)is indeed that defined by(3.4).Statement(3.10)combined with estimate(3.11)ensures that

Therefore,there exist

and a sequence(tn)n∈Nwhich goes to∞ as n→∞,such that

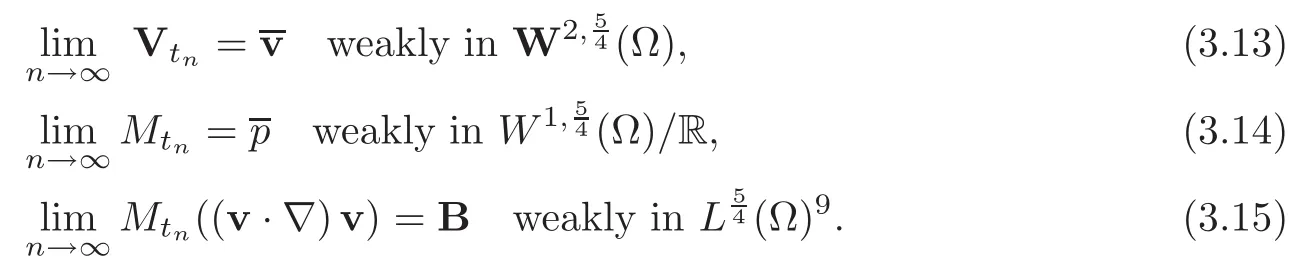
Moreover,the injection being compact.Then,

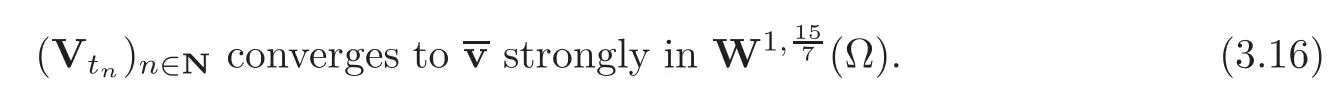
Step 2We check that∇=0 in an appropriate Lebesgue space.To do so,we first prove that ∇ ·Vt=0 in D′(QT)regardless of T>0.For any given ϕ ∈ D(QT),we have

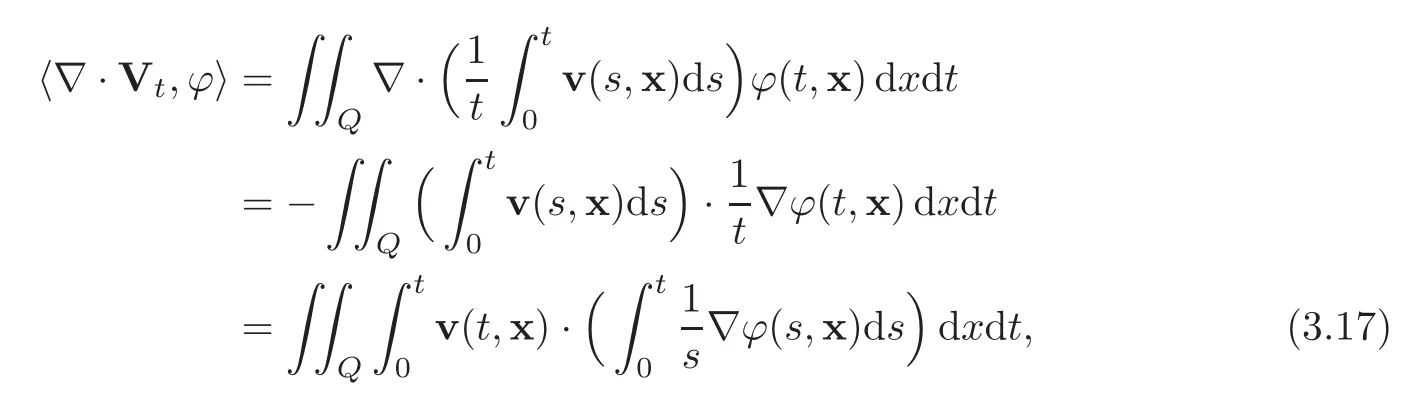
which holds because ϕ ∈ D(QT).Moreover,since ϕ ∈ D(QT),

Therefore,we deduce from(3.17)–(3.18)that

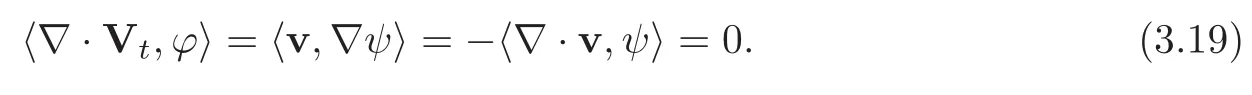
Because ∇ ·v=0,we have h∇ ·Vt,ϕi=0.Then,

Furthermore,by setting V0=v0,we get Vt∈ C([0,T],L2(Ω)),so that(3.20)becomes

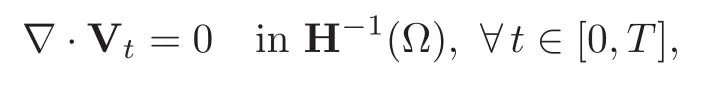
and in reality inby(3.16),and regardless of T>0,which allows us to take the limit as tn→∞,leading to∇·v=0 in L157(Ω).

Step 3We now take the limit in the momentum equation.Let ϕ ∈ D(Ω).Since ϕ,∇ϕ,∆ϕ ∈ L5(Ω),we deduce from(3.13)–(3.15)and the convergence to zero of(εtn)n∈Nin all Lp(Ω),p≤ 2,on the one hand,

and on the other hand,

which shows by(3.5)that(v,p)satisfies in D′(Ω),

Let F denote the tensor defined by

Aswe get

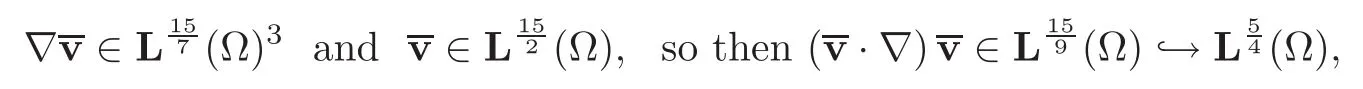
and we deduce thatHencesatisfies(3.7)in the sense of distributions.

Corollary 3.1The long-time velocityis a solution of the following variational problem:

the operators a and b being defined by(2.8).

Remark 3.1The proof of Theorem 3.1 contains the proof of the general identity,∀p≥1,∀T>0,∀t∈[0,T],

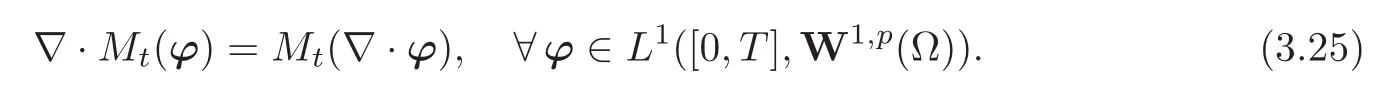
Furthermore,the same reasoning also yields

which is called the Reynolds rule.

3.3 Reynolds decomposition

We aim to identify the source term F that appears in(3.7),to link the results of Theorem 3.1 with the usual approach to modelling turbulence,by introducing the Reynolds decomposition and the Reynolds stress.

Let v be a given turbulent solution of the NSE,and p be its associated pressure.We respect the conditions for the application of Theorem 3.1,which ensures that we can split(v,p)into

where(v′,p′)stands for the f l uctuations around the mean field(v,p).We call the decomposition(3.27)–(3.28)a Reynolds decomposition.

To identify the source term F in(3.7),we start from(3.5)and notice that,according to the Reynolds rule(3.26),

We shall find out from the Reynolds decomposition that it suffices to study the convergence of

as t→ ∞,which yields what we call a Reynolds stress,denoted by σ(R).

Remark 3.2The definition ofand hence the Reynolds decomposition(3.27)–(3.28)and the Reynolds stress that we shall find,depend on the sequence(tn)n∈Nthat appears in Theorem 3.1,and we do not know if the limit of(Vt,Pt)t>0is solely defined when t→∞.As a result,we do not know if F is solely defined either,and even if it were,it is not known if(3.7)has a unique solution.All of these imply that without any further information,this analysis will not provide means and decomposition that are intrinsically defined.

3.4 Reynolds stress

Theorem 3.2Let(tn)n∈Nbe as in Theorem 3.1 and F as in(3.7).Then there existssuch that

(i)we can extract from(Mtn(v′⊗ v′))n∈Na subsequence,that we denote by(Mtn(v′⊗v′))n∈N,which converges to σ(R)weakly in

(ii)F= ∇ ·σ(R)in D′(Ω);

(iii)the following energy balance holds:

(iv)F is dissipative,in the sense

ProofRemember that Mtis defined by(3.1).We derive from(3.27)–(3.28)that

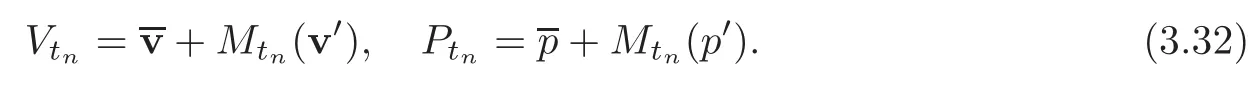
Therefore we deduce

the limit being weak inandrespectively.In addition(tn)n∈Ncan be chosen such that the convergence of(Mtn(v′))n∈Ntoward 0 is strong inbecause the injection

is compact.We now demonstrate each item of the above statement.

Proof of(i)By using decomposition(3.27),we write

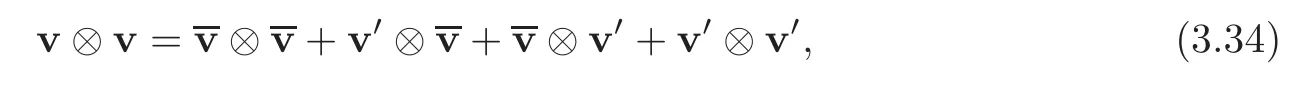
leading to

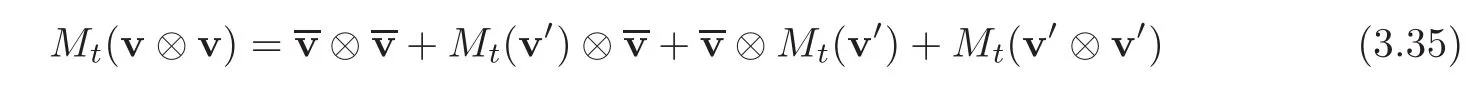
for each t>0.As bothandwe obtain from Hölder’s inequality,

In particular,(3.33)yields

strongly inMoreover,we infer from(3.2),combined with(2.23)and(2.26),that

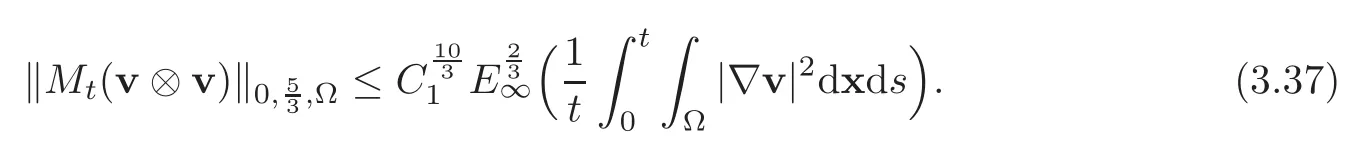
We are led to rewrite(3.35)in the form of the asymptotic expansion,which holds in

We deduce from the estimate(3.37)that(Mtn(v ⊗ v))n∈Nis bounded inTherefore,we can extract a subsequence(written likewise),which converges weakly into someThe expansion(3.38)shows that the sequence(Mtn(v′⊗v′))n∈Nweakly converges tolinked to ϑ by the relation

which proves(i).

Proof of(ii)According to(3.15)and the Reynolds rule(3.26),we note that∇·ϑ=B∈and therefore(3.23)combined with(3.39)yields F= ∇ ·σ(R).

Proof of(iii)As already quoted,Moreover,since=0 on Γ and ∇=0,we have∈ Vdiv(Ω).Consequently,we can take v as a test in formulation(2.13),which yields

We integrate(3.40)over[0,t]and divide the result by t,leading to

We take the limit of each term in(3.41).Firstly

which goes to zero when t→∞,due to the L2uniform bound(2.23).We also haveand Mtn((v·∇)v)converges toFortunately,we observe thatand thus,according to(3.23),

since it is easily verified from ∇=0 that

Finally,we deduce from Theorem 3.1 and Sobolev embeddings that(∇Vtn)n∈Nconverges strongly toin Lq(Ω)for alland in particular,for q=2,leading to

so the energy balance(3.30)follows from(3.41)–(3.44).

Proof of(iv)We start from the energy inequality(2.16)that we divide by tn,and we let n go to infinity.Using again the strong convergence of(∇Vtn)n∈Nto ∇v in L2(Ω)and the L2uniform bound as above,we obtain

which combined with(3.30)yields(3.31)and concludes the proof.

In summary,satisfies

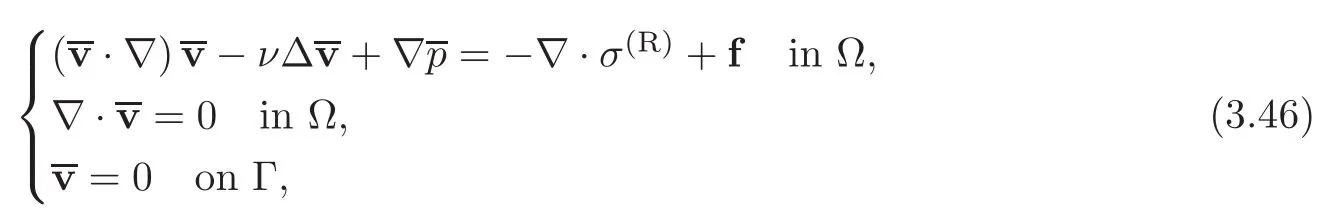
in the sense of distributions,where in addition,

AknowledgmentsThe author is very grateful to Professor Li Tatsien and the ISFMA in Fudan University,Shanghai,China,for the hospitality in the summer of 2013.

[1]Amrouche,C.and Girault,V.,On the existence and regularity of the solutions of Stokes problem in arbitrary dimension,Proc.Japan Acad.,67(5),1991,171–175.

[2]Batchelor,G.K.,An Introduction to Fluid Dynamics,Cambridge University Press,Cambridge,1967.

[3]Boussinesq,J.,Essai sur la théorie des eaux courantes,Mémoires Présentés par Divers Savantsl’Académie des Sciences,23(1),1877,1–660.

[4]Caffarelli,L.,Kohn,R.and Nirenberg,L.,Partial regularity of suitable weak solutions of the Navier-Stokes equations,Comm.Pure Appl.Math.,35(5–6),1982,771–831.

[5]Chcon Rebollo,T.and Lewandowski,R.,Mathematical and Numerical Foundations of Turbulence Models and Applications,Modeling and Simulation in Science,Engineering and Technology,Birkhäuser,Basel;Springer-Verlag,New York,2014.

[6]Hopf,E.,Ber die Anfangswertaufgabe fr die hydrodynamischen Grundgleichungen,Math.Nachr.,4,1951,213–231(in German).

[7]Kolmogorov,A.N.,The local structure of turbulence in incompressible viscous fluids for very large Reynolds number,Dokl.Akad.Nauk SSR,30,1941,9–13.

[8]Girault,V.and Raviart,P.A.,Finite Element Approximation of the Navier-Stokes Equations,Springer-Verlag,Berlin,1979.

[9]Feireisl,E.,Dynamics of Viscous Incompressible Fluids,Oxford University Press,Oxford,2004.

[10]Layton,W.,The 1877 Boussinesq conjecture:Turbulent fluctuation are dissipative on the mean flow,2014,to appear.

[11]Leray,J.,Sur le mouvement d’un liquide visqueux emplissant l’espace,Acta Mathematica,63,1934,193–248.

[12]Lions,J.L.,Quelques Méthodes de Résolution des Problèmes aux Limites non Linéaires,Dunod,Paris,1969.

[13]Prandtl,L.,über die ausgebildeten Turbulenz,Zeitschrift für Angewandte Mathematik und Mechanik,5,1925,136–139(in German).

[14]Reynolds,O.,An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous,and of the law of resistance in parallel channels,Philosophical Transactions of the Royal Society,174,1883,935–982.

[15]Ruelle,D.,Chance and Chaos,Princeton University Press,Princeton,1991.

[16]Sobolev,V.I.,Bochner integral,Hazewinkel,Michiel,Encyclopedia of Mathematics,Springer-Verlag,New York,2001.

[17]Stokes,G.,On the effect of the internal friction of fluids on the motion of pendulums,Transactions of the Cambridge Philosophical Society,9,1851,8–106.

[18]Tartar,L.,An introduction to Navier-Stokes equation and oceanography,Lecture Notes of the Unione Matematica Italiana,1,Springer-Verlag,Berlin;UMI,Bologna,2006.

[19]Tartar,L.,An introduction to Sobolev spaces and interpolation spaces,Lecture Notes of the Unione Matematica Italiana,3,Springer-Verlag,Berlin;UMI,Bologna,2007.

[20]Taylor,G.I.,Statistical theory of turbulence,Part I-IV,Proc.Roy.Soc.A.,151,1935,421–478.

[21]Temam,R.,Navier-Stokes Equations,Theory and Numerical Analysis,Reprint of the 1984 Edition,A.M.S.Chelsea Publishing,Providence,RI,2001.