An Optimal Design Method Based on Small Amplitude Homogenization∗

Sergio GUTIRREZ

(In Honor of the Scientific Contributions of Professor Luc Tartar)

1 Introduction

If one has two materials given in fixed volumes,to completely fill a domain and optimize an objective function by distributing each material in the best possible way,there are several examples showing that increasingly finer mixtures of both materials appear,and see for example[8],which points to the need of computing the effective or homogenized properties of such mixtures at the macroscopic scale,in order to appropriately evaluate the objective function and optimize over all possible ways to distribute the materials.Allowing such fine mixtures gives rise to the so-called relaxed problem.Unfortunately,closed formulas for effective properties of mixtures are known only for laminates and coated disks or balls,as far as we know.Even though for certain important problems one can show that those formulas are sufficient to find the optimal microgeometries(see[1]),there are many other problems for which it is not known whether those formulas are all that one needs.

One way around that difficulty comes by making the assumption that the two materials being employed are not very different,i.e.,the quotient of their relevant physical properties(heat conductivity,stiffness,permeability,etc.)is close to 1,because in such case one can use the tool of H-measures introduced by Luc Tartar in 1990(see[9]),to compute an approximation of the effective property,which is correct up to the second order in the contrast parameter,namely,the difference with respect to 1 of the quotient of the relevant values for each material.Under that assumption,an optimal design method has been devised in collaboration with Grégoire Allaire(see[2]),which is based on making an expansion of the state function with respect to the contrast parameter,and leads to a cascade of three boundary-value problems as follows:The first problem depends only on the properties of one of the materials,the one chosen as the reference material;the second problem depends upon the solution to the first problem and linearly upon the microgeometry,making then straightforward to pass to the limit in this problem for a minimizing sequence of microgeometries that converges weakly;finally,the third problem depends upon the solution of the second problem and directly upon the microgeometry in a linear form,which then leads to an overall quadratic dependence upon the microgeometry and it is for this problem that H-measures allow us to compute the correct relaxed problem,when taking weakly convergent sequences of microgeometries.The method was derived originally for elliptic state equations,but recently in[3],it was rigourously applied to the wave equation.

This paper is organized as follows:

(1)Motivation:Optimal design problems,relaxation by full homogenization.

(2)The optimal design method based on small amplitude homogenization.

(3)Numerical examples:Stress constrained compliance minimization,inverse problems.

(4)Conclusions.

In the previous paragraphs,we mentioned Luc Tartar only once in reference to the introduction of H-measures,but his mathematical contributions as follows are indeed fundamental to the subjects related to this work:Optimal design and homogenization.His intellectual clarity has enlightened several important areas of analysis and many scientists deeply appreciate his devotion to the advancement of science for the benefit of all mankind.

2 Optimal Design Problems

Let N ∈ {2,3}and Ω ⊂ RNwith its boundary divided into two portions∂Ω = ΓD∪ ΓN.Ω is filled with two materials having different,say,elastic properties,i.e.,different elasticity tensors C0and C1.The amount to use each of them is fixed.The material with the elasticity tensor C0is referred to as material 0,the reference material or the matrix material.The other material is mostly referred to as material 1.

Let χ be the characteristic function of the subset of Ω filled with material 1.Then χ is called the design variable.Then the elasticity tensor is

and we impose that

Given the external body force f and the surface traction g acting on ΓN,to determine under the standard assumption of linearized elasticity the state function u,which in this context physically corresponds to the displacement of each material point in the reference configurationΩ induced by the external forces and supporting conditions,we need to solve the following state equation:

with

We want to minimize an objective function given by

over the following set of admissible designs:

Namely,we would like to solve the following problem:

We want to construct a minimizing sequence{χn}for this problem and,if possible,find its limit.However,as mentioned in the introduction,solving this problem might lead to the appearance of microstructures,requiring us to compute the effective properties of these fine mixtures,namely,the need to introduce the notion of H-convergence.The following definition of H-convergence was introduced by Tartar and Murat in about 1976.

Definition 2.1Let Cn:be a sequence of(the fourth-order,uniformly elliptic and bounded)tensor valued fields and C:We say that CnH-converges to C if the following holds:For any f,g we have that if un∈ H1(Ω)Nare the solutions to

then unconverges weakly(in H1)to u∞and Cnε(un)converges weakly(in L2(Ω)N×N)to Cε(u∞),where u∞is the solution to

Given that(2.2)might not have a classical solution as a characteristic function in Uad,one uses H-convergence to relax it by defining

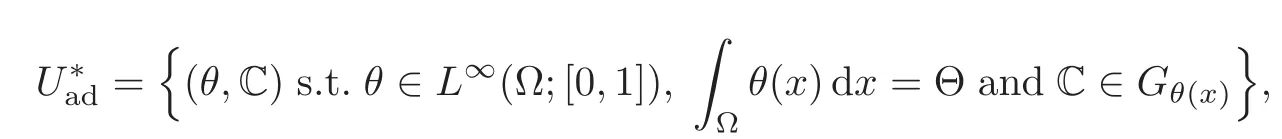
where Gθis the set of all possible H-limits of sequences of the form Cn=(1−χn)C0+χnC1and χn⇀ θ in L2,and solve instead

where it is understood that C in(2.1)is the second component of a pair in

A Serious ProblemGθis known in very few cases.

For diffusion,it is known when at least one of the two starting materials is isotropic.In linear elasticity,only some bounds are known(see[7]).

Then,in the next section,we show a way to bypass the need to know Gθby making some approximations under some extra assumptions.

3 Small Amplitude Homogenization

The following method was introduced in collaboration with Grégoire Allaire(see[2]).We assume that

with η ∈ (−1,+∞)and the contrast parameter between the stiffness of both materials is assumed to be known.In the isotropic case,the Young moduli would be related as E1=(1+ η)E0and the Poisson ratios would coincide ν1= ν0.

Then we now have

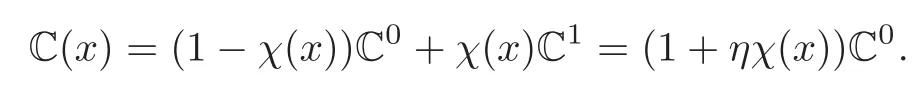
Since C is affine on η,we have that the state function u is analytic in η,and then we can make an asymptotic expansion of u as

which allows us to separate scales,because we will have a cascade of boundary value problems,one for each term in the expansion of u.

That is to say,the problem for u0is

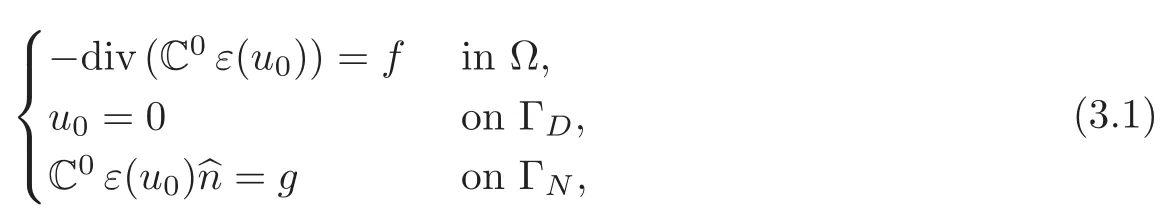
and then u0does not depend upon χ.

The problem for u1becomes

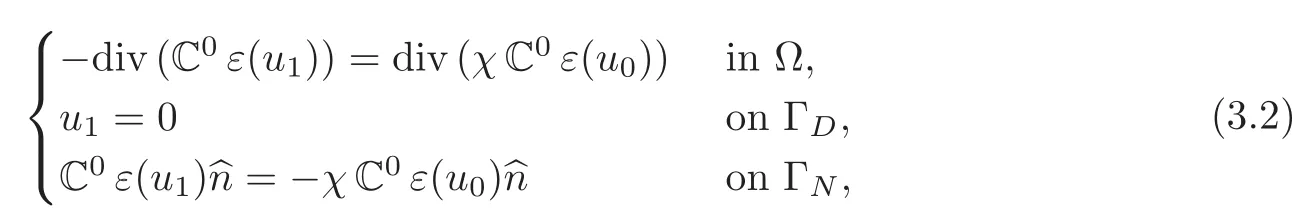
and then we can define a pseudo-differential operator relating ε(u1)to χ,using the Fourier transform F on the so-called fast variable,as follows:

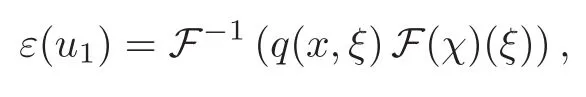
where,if C0is isotropic with Lamé parameters µ and λ,and σ0=C0ε(u0),we have

Finally,for u2,we have

Then there is a quadratic interaction between χ and u1,which will give a correction term when relaxing.That is,if χn⇀ θ,we have a subsequenceweakly in H1,with u1being the solution to

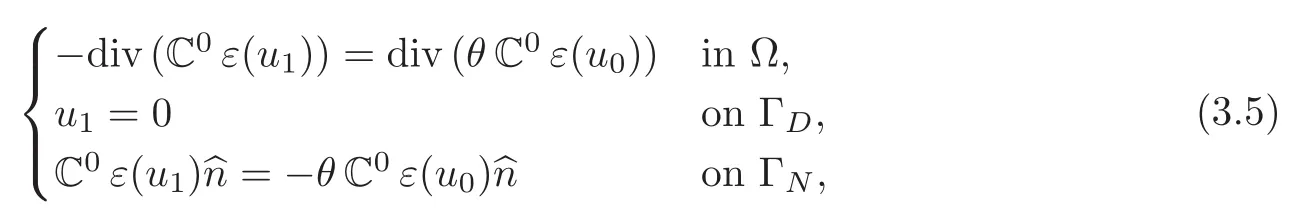
andweakly in H1,with u2being the solution to

where M is characterized through its associated quadratic form over the space of symmetric N×N matrices,namely,

where SN−1is the unitary sphere in RNand ν(x,dξ)is a probability measure on SN−1derived from the H-measure induced by the sequence χn− θ.The general result from[9]follows.

Theorem 3.1Letbe a sequence of functions defined in RNwith values in Rpwhich converges weakly to 0 in L2(RN)p.There exists a subsequence(still denoted by hǫ)and a family of complex-valued Radon measures(νij(x,ξ))1≤i,j≤pon RN×SN−1such that,for any functions φ1,φ2∈ C0(RN)and ψ ∈ C(SN−1),it satisfies

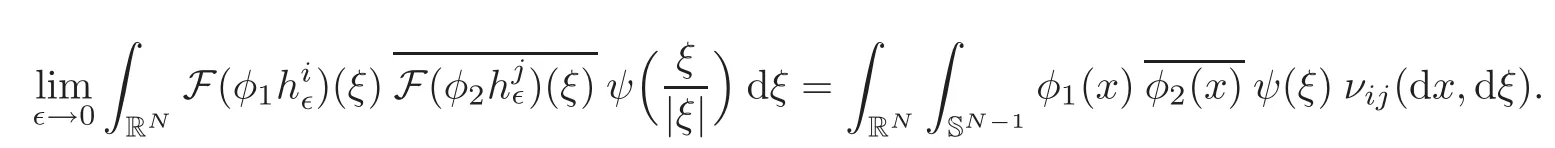
The matrix of measures ν =(νij)1≤i,j≤pis called the H-measure of the subsequence hǫ.

Then,to simplify the exposition,we concentrate on objective functions of the form

and if we additionally assume that j is of class C3,we make an expansion by using u0as the solution to(3.1),u1as the solution to(3.2),and u2as the solution to(3.4),as follows:

Then,after relaxation and neglecting the error term,using now u1as the solution to(3.5)and u2as the solution to(3.6),while u0is the same as before,we get

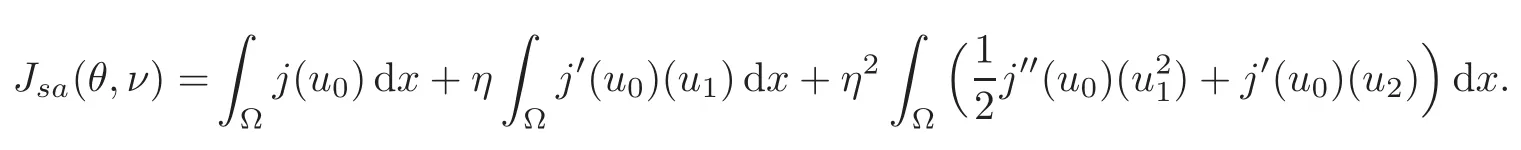
The participation of ν is only through the dependence of u2upon M,but then,using the following adjoint problem:

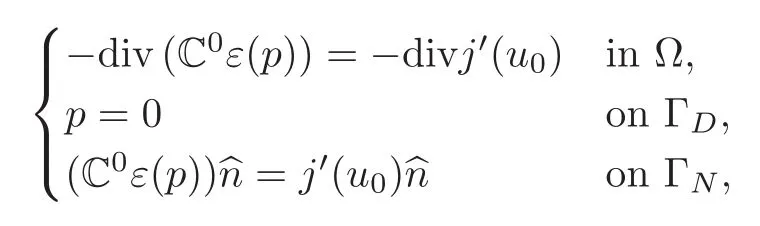
we can derive the following relationship,where “:” denotes the tensor inner product:

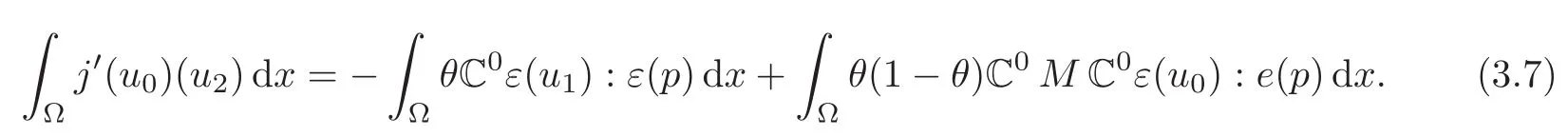
Therefore,we can write the relaxed approximation of the objective function as

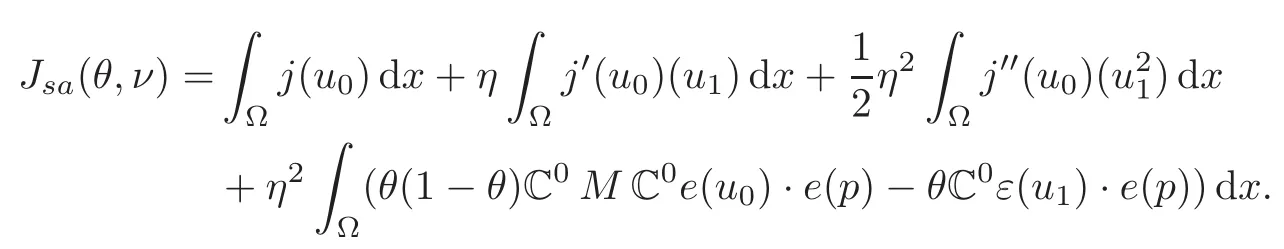
Then,using σ =C0e(u0)and σ′=C0e(p),we find the optimal microstructure at each point by solving

Then,by computing first u0and p,which do not depend upon θ,we can find the optimal microstructure at each point,namely,a rank-1 laminate in the direction that solves the last minimization problem,in proportion θ of material 1 and 1− θ of material 0.Then replacing this minimum value in Jsa,we can write it as a function depending only upon θ and derive a gradient-based optimization algorithm.We do not provide further details about the algorithm,as they can be found in the papers dealing with specific applications.In the next section,we present two of those specific applications.

4 Numerical Examples

4.1 Compliance minimization under a stress constraint

The work was done in collaboration with Zegpi,a former graduate student.For details,please see[5].

Compliance minimization in linearly elastic structures was amply studied.It aims at finding the stif f est structure by placing the reinforcement at the best position and it is one case in which the solution by full homogenization can be found among sequential laminates.Unfortunately,some of these solutions exhibit high stress concentration,making them less useful since they will not be able to sustain a large load,due to premature cracking.Therefore,we propose to use the optimization method introduced in Section 3 to still minimize compliance,but impose additionally a constraint on the average stress in the critical region.For the case of a short cantilever beam,stresses concentrate in the vicinity of the loading zone and near the extremes of the fixed boundary,namely,the black zones in Figure 1.Here we concentrate on the first situation,where stress peaks are larger,but the results for the second situation are similar.We denote by ω the black zone near the loading.

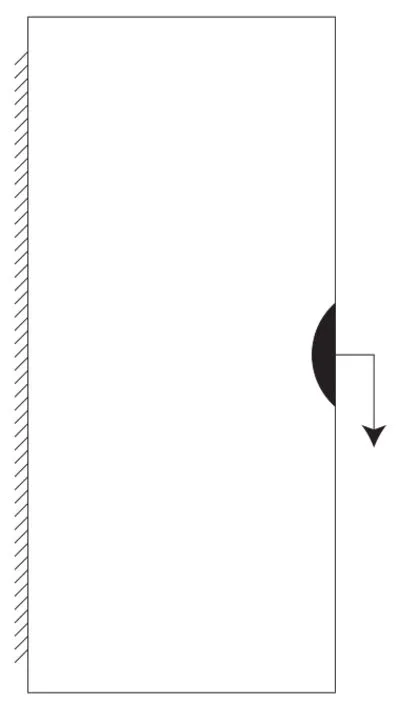
Figure 1 Short cantilever.Stress is constrained on the black zones.Modif i ed from[5].

If f=0,i.e.,we neglect body forces,the compliance is

Let k be a C3function of σ.Then we consider

which we impose to be less than or equal to a prescribed value Tmax.Then using the notation

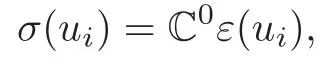
we approximate K as

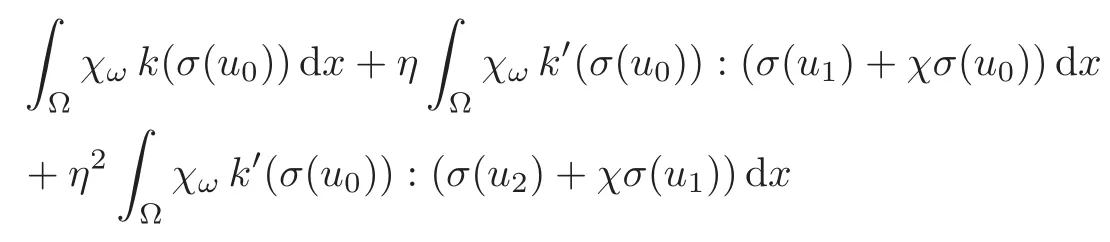
Then making a similar relaxation for the approximation of K as it can be done for the objective function J,appropriately choosing the optimal direction of lamination,and introducing a Lagrange multiplier l for the stress constraint,we have

which we minimize.

In Figure 2,we present the standard solution for large contrast,which is obtained after penalization of mixtures in the problem relaxed by full homogenization,but is now used for the case of moderate contrast,namely 1 to 2.There we can observe the high stress concentration.

Figure 2(a)Optimal solution for compliance minimization using full homogenization for large contrast.(b)Stress distribution using η = −0.5.(c)Zoom around the loading zone.Modif i ed from[5].

In Figure 3,we present the solution to compliance minimization using small amplitude homogenization,without restricting the stress.We see that the stress peaks are even higher than the ones in Figure 2.

Figure 3(a)Optimal solution for compliance minimization using small amplitude homogenization.(b)Stress distribution.(c)Zoom around the loading zone.Modif i ed from[5].

Finally,in Figure 4,we present the solution for compliance minimization using small amplitude homogenization,and now restricting the stress.We see that the stress peaks have descended significantly compared with the ones in Figure 3.In Table 1,we compared the results in these three cases and made a direct comparison between the two latest ones.As expected,the compliance in the stress constrained case is higher than that when no such constraint is applied,but the increase is just 3.2%,small if compared with the diminution in the peak stress of 38.4%.

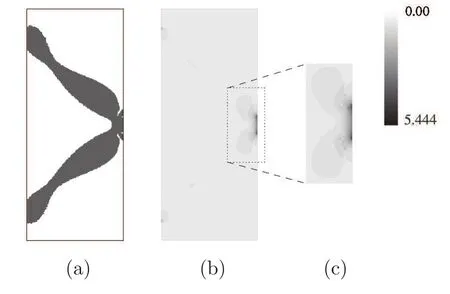
Figure 4 (a)Optimal solution for compliance minimization using small amplitude homogenization under stress constraint near the loading zone.(b)Stress distribution.(c)Zoom around the loading zone.Modif i ed from[5].

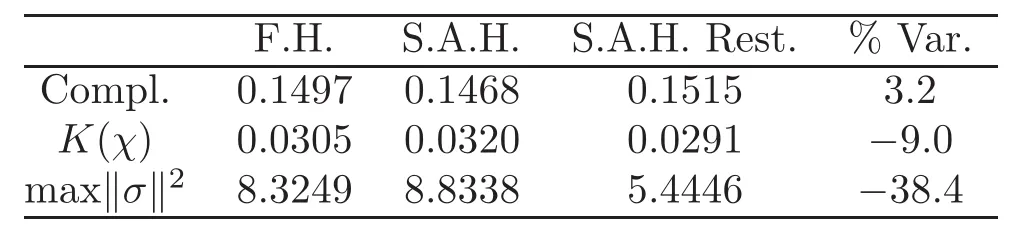
Table 1 Ef f ect on the compliance and stress when restricting the average stress in the loading zone

4.2 Inverse problems

The work was done in collaboration with Mura(de,Chile),Santa(de Chile)and Vito.

We consider now that Ω is a solid body,still made of two materials,but now the interpretation of material 1 is that of a defect inside the body,whose location we want to find by measuring displacements only on part of the boundary of Ω.Let Γ ⊂ ΓNbe the zone,where we measure the actual displacement urand we want to find the defect location χ that minimizes

with u the displacements coming from a guess on the location of the defect.One would also like to determine the contrast parameter η and the size of the inclusion Θ,but we assume these two values to be known and concentrate only on determining the location of the defect.

First we did only numerical trials,and then urcorresponds to the solution to the state problem with full knowledge of the location of the defect.This was done in[6]applying a shearing force to the doubly fixed beam shown in Figure 5,where the darker zones correspond now to defects having 10%less stiffness than the rest of the beam,namely η = −0.1.

Figure 5 Numerical experimental setting.

The results of applying the method to this physical setting are presented in Figure 6,when the algorithm is given different sizes of the defect it has locate and only Figure 6(c)is for the correct size.There we see that the method performs quite well for slender objects.For non-slender objects,the results are not so good.

Figure 6 Solutions when using a different volume for the defect with multiplicative factors:(a)0.1(1.1%of|Ω|),(b)0.5(5,7%of|Ω|),(c)1.0(exact),(d)1.5(17,2%of|Ω|),(e)2.0(22.9%of|Ω|).η= −0.1.

Given the success in the numerical trials,we decided to apply the method to physical experiments.Due to experimental conditions,it is necessary to modify the setting.These results were presented in[10].We consider now steel plates,1 cm thick,loaded in-plane and we measure the displacements on the side opposite to the load.In Figure 7,we show the experimental setting,and in Figure 8,we show the final results applying an adaptive scheme to select loading and measuring positions(see[4]).We consider these results as quite promising,but some new lessons were learned in relation to the experimental use of the method as follows:The fixed boundaries are very difficult to reproduce for loadings sufficiently large,so that they permit the method to work,and therefore the fixed boundary conditions are replaced by small known displacements;the best results are obtained when the defect is located between the load and the measurement zones;larger measurement zones are not necessarily beneficial.

Figure 7 Test setup.

Figure 8 Results of detection for two specimens,having a shorter measurement zone(above)compared with the used are below.Highlighted:Load zone(red)and Measurement zone(blue).η=−0.6.

5 Conclusions

The main conclusion is that the optimal design method based on small amplitude homogenization presented above,does provide the mathematical basis for implementing computational methods to solve relevant problems in engineering,even beyond the constraint on the contrast between the stiffness of both materials being small,since,as shown for stress-constrained compliance minimization,a contrast of 100%still allows the results to be quite acceptable.

The computational requirements for the 2-D examples shown above are quite modest.The mathematical computations needed for the 3-D version of the method are direct and its computational implementation is not difficult.In fact,we have done some numerical experiments and they have worked well.Doing physical experiments in 3-D is possible,but it requires more expensive laboratory equipment.

Some other applications of the method have also given promising results,like solving inverse problems with non equilibrium state equations and optimizing the location of a less permeable core inside the wall of an embankment dam.

AcknowledgementsThe author acknowledges the kind hospitality and partial funding of Fudan University,to attend the international conference on nonlinear and multiscale PDEs:Theory,numerics and applications;held in September 2013 in Shanghai to honor Luc Tartar.

[1]Allaire,G.,Shape Optimization by the Homogenization Method,Springer-Verlag,New York,2002.

[2]Allaire,G.and Gutiérrez,S.,Optimal design in small amplitude homogenization,ESAIM Mathemtical Modelling and Numerical Analysis,41(3),2007,543–574.

[3]Allaire,G.and Kelly,A.,Optimal design of low-contrast two phase structures for the wave equation,Math.Mod.Meth.Appl.Sci.,21,2011,1499–1538.

[4]Gutiérrez,S.and Mura,J.,An adaptive procedure for defect identification problems in elasticity,Comp.Rend.Mec.,338,2010,402–411.

[5]Gutiérrez,S.and Zegpi,E.,Stress constrained compliance minimization by means of the small amplitude homogenization method,Structural and Multidisciplinary Optimization,49(6),2014,1025–1036.

[6]Mura,J.and Gutiérrez,S.,Detection of weak defects in elastic bodies through small amplitude homogenization,Inverse Problems in Science and Engineering,19(2),2011,233–250.

[7]Milton,G.,The Theory of Composites,Cambridge University Press,Cambridge,2001.

[8]Murat,F.and Tartar,L.,Calcul des variations et homogénéisation,Les Méthodes de l’homogénéisation théorie et applications en physique,Coll.Dir.Etudes et Recherches EDF,57,1985,319–369;English translation:Topics in the mathematical modelling of composite materials,Progress in Nonlinear Differential Equations and their Applications,A.Cherkaev and R.Kohn(eds.),31,Birkhäuser,Boston,1997.

[9]Tartar,L.,H-measures,a new approach for studying homogenisation,oscillations and concentration effects in partial differential equations,Proc.Royal Soc.Edinburgh,115(A),1990,193–230.

[10]Vito,A.,Gutiérrez,S.and Santa-María,H.,Experimental validation of a computational method for detecting the location of a defect,submitted.