The Role of a Vanishing Interfacial Layer inPerfect Elasto-Plasticity

Gilles A.FRANCFORT Alessandro GIACOMINI

(Dedicated to Luc Tartar Notwithstanding His Dislike for Elasto-Plasticity)

1 Introduction

1.1 Introductory remarks

This paper focuses on the behavior of a two-phase elasto-plastic material in a small strain setting.

The topic was first tackled mathematically in[10–11],and then,after a twenty five year long interlude,revisited in[3]within the framework of the rapidly expanding variational theory of rate independent evolutions(see,e.g.,[8]).The ensuing functional setting results in strain fields that can concentrate on sets of co-dimension at most 1 and displacement fields that can in particular jump along rectif i able hypersurfaces.So,as Luc Tartar repeatedly pointed out,the mathematical models of small strain elasto-plasticity are prima facie inconsistent with the small strain assumption which they were born out of.We gladly acknowledge this inconsistency which cannot be reconciled at present through the consideration of models of finite plasticity for lack of any kind of consensus of what such models could be.

In[5],we derived what we believe to be the first evolution model for a multi-phase heterogeneous elasto-plastic material,although earlier work[9]previously analyzed a subclass of possible multi-phase heterogeneities.In any case,our results,specialized to a two-phase setting,demonstrate that the correct stress constraint on the interface only involves the resolved shear stress and that the corresponding set of admissible resolved shear stresses is that which corresponds to the intersection of the set of admissible stresses for each phase.This leads to a well-defined interfacial flow rule which,to the best of our knowledge,cannot be found in the abundant literature on elasto-plasticity,be it on the mathematical,or on the mechanical side.

In this paper,we propose to investigate the impact of a vanishingly thin interface between the two phases and to demonstrate that such an interface is felt in the resulting two-phase model through an interfacial dissipation lower than that predicted by the pure two-phase problem.This question was suggested to us by Mark Peletier whom we gratefully acknowledge.Of course,we cannot consider a bona fide thin layer of a third material because the question of the modeling of the interface between that layer and the two phases would immediately render the investigation moot.Rather,we will consider a continuously varying set of admissible stresses near and on the interface and then propose to pass to the limit in the thickness of the transition.

The result is given in Theorem 3.1 and further interpreted in Section 4.In a nutshell,we establish that any modeling of the interface as the limit of a vanishing third phase whose set of admissible stresses is smaller than the intersection of those in both phases will result in a lower interfacial dissipation,and hence that the pure two-phase material is the maximally dissipating model for the interface.

So,in conclusion,it is indeed possible to model an elasto-plastic interface between two elasto-plastic phases.However,the interfacial dissipation cannot be chosen arbitrarily.It must be so that it is below that generated by the intersection of the sets of admissible stresses of both phases.

1.2 Notations and preliminaries

General NotationsFor A ⊆ RN,χAdenotes the characteristic function of A,i.e.,χA(x)=1 for x ∈ A and χA(x)=0 for x 6∈ A.The indicator function of A,denoted by IA,is defined as IA(x)=0 for x ∈ A,and IA(x)=+∞ for x 6∈ A.The symbol⌊A stands for “restricted to A”.

We will denote by LNthe N-dimensional Lebesgue measure and by HN−1the(N −1)-dimensional Hausdorf fmeasure,which coincides with the usual area measure on sufficiently regular sets(see,e.g.,[4,Section 2.1]or[2,Section 2.8]).

MatricesWe denote bythe set of N×N-symmetric matrices and bythe set of trace-free elements ofIf σ is an element ofthen σDis its deviatoric part,i.e.,its projection onto the subspaceoforthogonal to the identity matrix for the Frobenius inner product.The symbol·stands for that inner product and the symbol|·|for the Frobenius norm.The set of symmetric endomorphisms onis denoted byFor a,b∈RN,a⊙b stands for the symmetric matrix such that

Functional SpacesGiven E⊆RNmeasurable,1≤p<+∞,and M a finite-dimensional normed space,Lp(E;M)stands for the space of p-summable functions on E with values in M,with associated norm denoted by k·kp.Given A ⊆ RNopen,H1(A;M)is the Sobolev space of functions in L2(A;M)with distributional derivatives in L2.

Finally,let X be a normed space.We denote by BV(a,b;X)and AC(a,b;X)the space of functions with bounded variation and the space of absolutely continuous functions from[a,b]to X,respectively.The total variation of f∈BV(a,b;X)is defined as

MeasuresIf E is a locally compact separable metric space,and X a finite dimensional normed space,Mb(E;X)will denote the space of finite Radon measures on E with values in X.For µ ∈ Mb(E;X),we denote by|µ|its variation measure.The space Mb(E;X)is the topological dual ofthe set of continuous functions u from E to the vector dual X∗of X which vanish at the boundary,i.e.,for every ε>0,there exists a compact set K ⊆ E with|u(x)|< ε for x 6∈ K.

The(Kinematic)Space BDLet Ω⊂RNbe open and bounded.The displacement field u lies in the space of functions of bounded deformations

endowed with the norm

We refer the reader to,e.g.,[12,Chapter 2]and[1]for background information.

Besides elementary properties of BD(Ω),we will only appeal to the structure of Eu as a Radon measure:More precisely,as is the case for functions of bounded variation,the measure Eu decomposes as

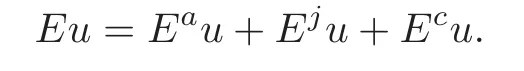
Here Eau denotes the part of the measure adsolutely continuous with respect to LN,so that

The singular part is further decomposed into a jump part Eju and a Cantor part Ecu.Specifically,

where Justands for the jump set of u(see[2,Definition 3.67]),[u]being the jump of u across Ju,while Ecu vanishes on Borel sets which are σ-finite with respect to the area measure HN−1(see[1,Proposition 4.4]).

Finally,we say that

iff

The(Static)Space ΣLet Ω ⊂ RNbe open and bounded with a Lipschitz boundary.We set

It is classical that,ifwith div σ ∈ L2(Ω;RN),σν is well-defined as an element of H−12(∂Ω;RN),ν being the outer normal to ∂Ω.

More generally,consider an arbitrary Lipschitz subdomain A ⊂ Ω with outer normal ν,and∆ ⊂ ∂A open in the relative topology.We can define the restriction of σν on ∆ by testing against functions in H12(∂A;RN)with compact support in ∆.This amounts to viewing σν as an element of the dual to

If σ ∈ Σ,then,in the spirit of[6,Lemma 2.4],we can define a tangential component[σν]τof σν on ∆ such that

Indeed,consider any regularizationof σ onsuch that

Define the tangential component[σnν]τ:=(σn)ν−((σn)ν·ν)ν.It is readily seen that[σnν]τ=[(σn)Dν]τ(the tangential component of(σn)Dis defined analogously).Since x 7→ ν(x)is an L∞(∆;RN)-mapping,there exists an L∞(∆;RN)-function[σν]τsuch that,up to a subsequence,

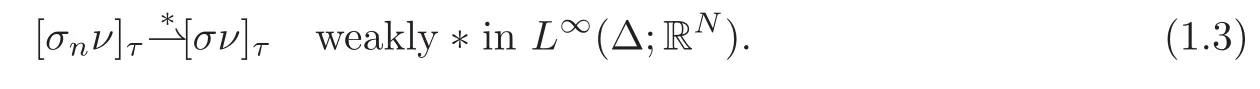
If σD≡ 0,then clearly,[σν]τ≡ 0,so that[σν]τis only a function of(σn)Dwhich we will denote henceforth by[σDν]τ.Notice that[σDν]τmay depend upon the approximation sequence{σn}n(or at least upon{(σn)D}n).

Finally,if∆is a C2-hypersurface,i.e.,a C2-submanifold of RNof dimension N−1,then[σDν]τis uniquely determined as an element of L∞(∆;RN).Indeed,for everywith support compactly contained in∆(that is,by density

where

Since the normal component(ϕ ·ν)ν of ϕ with respect to ∆ belongs toin view of the regularity of ν on ∆,the definition of(σν)νis meaningful.

2 Energetic Quasi-static Evolutions

In this section,we review the variational formulation for a heterogeneous quasi-static evolution in perfect plasticity.When the spatial dependence of the convex set of admissible stresses is continuous,the problem was investigated in[9].However,in the case where the heterogeneity is made of the juxtaposition of several phases with no particular ordering properties,then the reader should refer to[5].Of course,both works find their root in the seminal paper[3]in which elasto-plastic evolution was analyzed as a variational evolution.

The Reference Conf i gurationIn all that follows,Ω⊂RNis an open bounded set with(at least)Lipschitz boundary and exterior normal ν.Further,the Dirichlet part Γdof ∂Ω is a non-empty open set in the relative topology of∂Ω with boundary ∂⌊∂ΩΓdin ∂Ω and we setReproducing the setting of[5,Section 6],we introduce the following definition.

Definition 2.1We will say that ∂⌊∂ΩΓdis admissible iff,for anywith

where f ∈ LN(Ω;RN)and g∈ L∞(Γt;RN),and everysuch that there exists an associated pair(u,e)with

the distribution,defined for all

extends to a bounded Radon measure on RNwith|hσD,pi|≤ kσDk∞|p|.

Definition 2.1 covers many “practical” settings like those of a hypercube with one of its faces standing for the Dirichlet part Γd.See[5,Section 6]for that and other such settings.

Remark 2.1(2.2)defines a meaningful distribution on RN.Indeed,according to[5,Proposition 6.1],ifis such that divσ ∈ LN(Ω;RN)andthenfor every 1≤r<∞with

for some Cr>0.On the other hand,u ∈ LN/N−1(Ω;RN)in view of the embedding of BD(Ω)into LN/N−1(Ω;RN).Further,u has a trace on ∂Ω which belongs to L1(∂Ω;RN).Finally note that,if σ is the restriction to Ω of a C1-function and if HN−1(∂⌊∂ΩΓd)=0,then an integration by parts in BD(see[12,Chapter 2,Theorem 2.1])would demonstrate that the right-hand side of(2.2)coincides with the integral of ϕ with respect to the(well-defined)measure σDp.

Further,we assume that Ω is made up of two phases Ω1,Ω2,together with the phase interface.Those phases are disjoint open sets with Lipschitz boundary.We haveand denote by Γ the inner interface,i.e.,

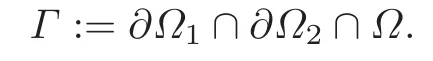
We assume the existence of a compact set S⊂Γ with HN−1(S)=0 such that

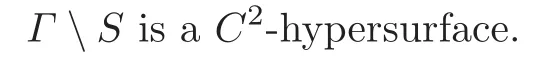
Finally,setting

S′is taken to be such that

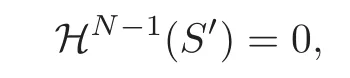
and we set

A domain Ω that satisfies the collection of those(minimal)assumptions will be referred to henceforth as a C2-geometrically admissible multi-phase domain.

Kinematic AdmissibilityGiven the boundary displacement w ∈ H1(Ω;RN),we adopt the following definition.

Definition 2.2(Admissible Conf i gurations)A(w),the family of admissible configurations relative to w,is the set of triplets(u,e,p)with

and such that

where ν denotes the outer normal to ∂Ω and(w−u)is to be understood in the sense of traces.

The function u denotes the displacement field on Ω,while e and p are the associated elastic and plastic strains.In view of the additive decomposition(2.3)of Eu and of the general properties of BD functions recalled earlier,p does not charge HN−1-negligible sets.Moreover,given a Lipschitz hypersurface D ⊂ Ω dividing Ω locally into the subdomains Ω+and Ω−,

where ν is the normal to D pointing from Ω−to Ω+,and u±are the traces on D of the restrictions of u to Ω±.Since p is assumed to take values in the space of deviatoric matricesis perpendicular to ν,so that only particular plastic strains are activated along D.

The Elasticity TensorThe Hooke’s law is given by an elementsuch that

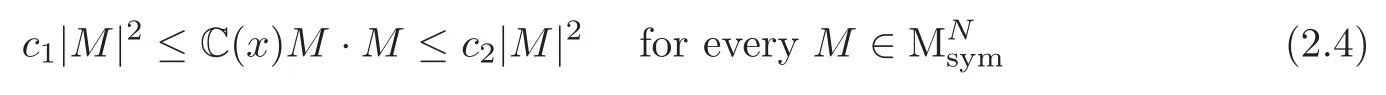
with c1,c2>0.

For everywe set

Admissible StressesIn elasto-plasticity,the deviatoric part of the stress σ is assumed to be restricted by the yield condition.For heterogeneous materials,this means that,at a.e.x∈Ω,there exists a convex compact setthe set of admissible stresses,such that σD(x)∈ K(x).

We say that the multimap x ⊸ K(x)is continuous on Ω if it satisfies the lower semicontinuity condition

∀ε>0,∃Uxopen s.t.x∈ Uxand K(x)⊂ K(y)+εB(0,1)for every y∈ Ux,

together with the upper semi-continuity condition

∀ε>0,∃Uxopen s.t.x∈ Uxand K(y)⊂K(x)+εB(0,1)for every y∈ Ux.

In that case,we further assume that the sets K(x)cannot be too small or too large,i.e.,there exist c3,c4>0 such that

In the present setting,the heterogeneity is the result of the assembly of two distinct phases with associated sets of admissible stresses K1and K2with

Then,the multimap x ⊸ K(x)is not a priori defined on the interface Γ,nor on S′.We define it on ΓS as

where ν(x)is the associated normal to Γ ,and[·]τdenotes the orthogonal projection to the hyperplane tangent to Γ at x.Notice that K(x)is a cylinder inOn S ∪ S′,we define K(x)arbitrarily as B(0,c3).

Henceforth,we refer to this case as the pure two-phase case.

The Dissipation PotentialThe Legendre transform of IK(x)yields the dissipation potentialgiven,for every x∈ Ω ∪ Γdand everyby

It is easily seen that,in the continuous as well as the pure two-phase cases,the map ξ 7→H(x,ξ)is convex and positively one-homogeneous,while H is Borel.

In the pure two-phase case,note that,for x∈ΓS,H reads as

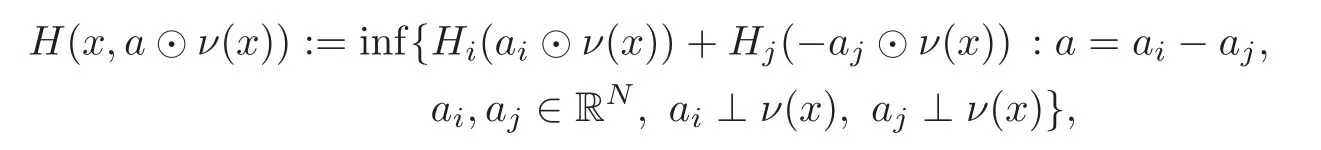
if ξ=a⊥ ν(x),and

Above and throughout the rest of this paper,

Finally,

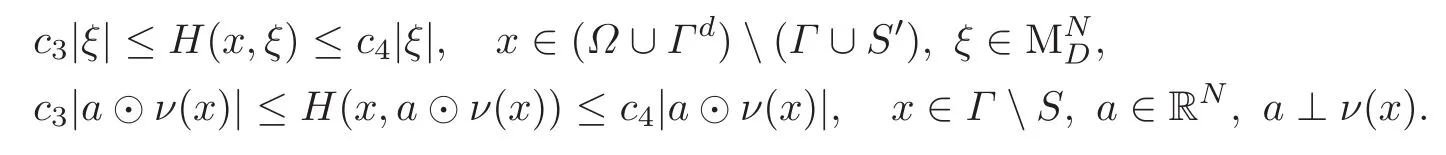
Remark 2.2In the two-phase case,we can decide that the admissible stress set on the interface is not as described through(2.7),but rather it is associated with some compact convex set K3containing 0.Then,mimicking(2.7),we define

on Γ S and complete the definition of K by B(0,c3)on S ∪ S′.

The resulting dissipation potential H,defined on ΓS as

and

can then be seen to enjoy the same properties as in the pure two-phase case,provided that

We call this latter setting the two-phase+interface case.

For every admissible plastic strain p∈P,we define the dissipation functional as

wheredenotes the Radon-Nikodym derivative of p with respect to its variation|p|.

If t 7→ p(t)is a map fromwe also define,for every[a,b]⊆ [0,T],

to be the total dissipation over the time interval[a,b].

Body and Traction ForcesFor simplicity,we do not consider any kind of force loads in this study.Adding those would only render the argument less legible.The results would be identical,provided that suitable safe loads conditions are satisfied(see[3,Section 2.2]).

Prescribed Boundary DisplacementsThe boundary displacement w on Γdfor the time interval[0,T]is given by the trace on Γdof some

In what follows,the energetic formulation of the quasi-static evolution is detailed in the footstep of[3]:The two ingredients of such evolutions are a stability statement at each time,together with an energy conservation statement that relates the total energy of the system to the work of the loads applied to that system.

Definition 2.3(Energetic Quasi-static Evolution)The mapping

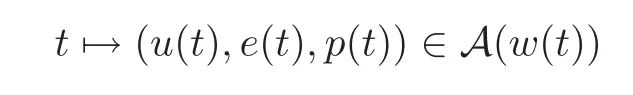
is an energetic quasi-static evolution relative to w iff the following conditions hold for every t∈[0,T]:

(a)Global stability:For every(v,η,q)∈ A(w(t)),

(b)Energy equality:and

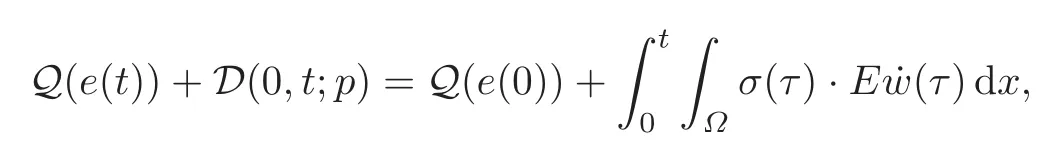
where σ(t):=Ce(t).

The following result was proved in[9,Theorem 3.14]for the continuous setting,or[5,Theorem 2.7]for the pure two-phase setting;note that,in either case,more general domains are admissible than those considered here.

Theorem 2.1(Existence of Quasi-static Evolutions)Suppose that Ω is a C2-geometrically admissible multi-phase domain.Assume that(2.4)and(2.10)are satisfied,and let(u0,e0,p0)∈A(w(0))satisfy the global stability condition(2.11).Finally,assume that the multi-map x⊸K(x)either is continuous,or corresponds to a pure two-phase case.

Then there exists a quasi-static evolution{t 7→ (u(t),e(t),p(t)),t∈ [0,T]}relative to the boundary displacement w such that(u(0),e(0),p(0))=(u0,e0,p0).Finally the Cauchy stress

is uniquely determined by the initial conditions.

Remark 2.3The following regularity property holds true(see[3,Theorem 5.2]and[5,Proposition 2.11]):

withAlso,the total dissipation D(0,t;p)is absolutely continuous.

The extent to which the aforementioned energetic quasi-static evolutions are also classical evolutions is described in detail in e.g.[5,Section 3].For our purpose,it suffices to note that the following result holds.

Remark 2.4Any quasi-static evolution in the sense of Definition 2.3 satisfies the balance equations

and the admissibility constraint in the phases

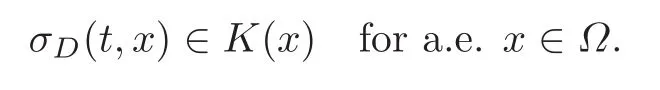
3 A Model with a Vanishing Interfacial Layer

In this section,we wish to view the two-phase behavior as the limit of a smoothly varying multi-map x ⊸ Kε(x)as the smoothing parameter ε tends to 0.To this effect,we consider the following two continuously increasing multi-maps:

where

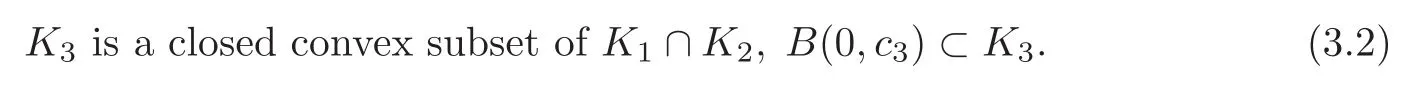
Remark 3.1For example,one could take Ki(τ)= τK1+(1− τ)K3.

We then consider

and define

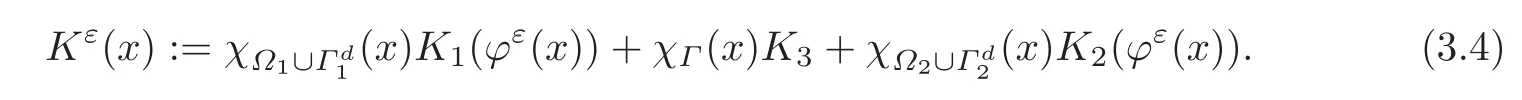
The associated elasto-plastic model may be viewed as a two-phase model with a continuous transition to a smaller admissible set of stresses,namely K3,near the interface Γ.

Since the associated multi-map x ⊸ Kε(x)is obviously continuous and satisfies(2.5),Theorem 2.1 applies and delivers an energetic quasi-static evolution

with associated dissipation potential Hε(x,ξ):=sup{τ·ξ:τ∈ Kε(x)}and associated total dissipation Dε(0,t;pε).Remark that,for i=1,2,

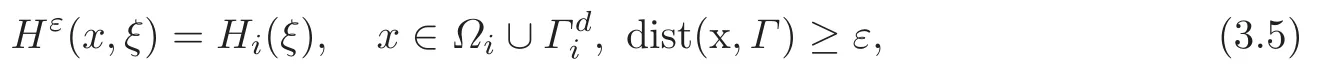
whereas,since the maps Ki(τ)are increasing,

Further,for the sake of simplicity,we assume that

so that the initial minimizing state of the ε-problem is always(0,0,0).

Define

and the associated dissipation potential

We also define,with obvious definitions,the dissipation potential H and the total dissipation D.

In the context of Remark 2.2,the definitions above correspond to a two-phase+interface case.We propose to prove the following theorem.

Theorem 3.1(An Evolution for the Two-Phase+Interface Case)Assume that Ω is a C2-geometrically admissible multi-phase domain and that assumptions(2.4),(2.10),(3.1)–(3.7)are satisfied.Also assume the admissibility of∂⌊∂ΩΓd(see Definition 2.1).

There exists a subsequence of{ε}(that we do not relabel)and a quasi-static evolution t 7→(u(t),e(t),p(t))relative to w in the sense of Definition 2.3 with

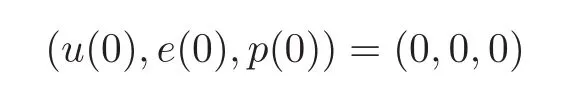
and H defined through(3.9)such that

for every t∈[0,T].Finally,for every t∈[0,T],

Remark 3.2The above theorem implies in particular the existence of a quasi-static evolution for the dissipation potential associated to K(x).The ensuing evolution is different from that obtained in the absence of the vanishing interface characterized by the admissible set K3.Indeed the latter would correspond to an identical K(x)except on ΓS where it would be given through(2.7)whereas it is given here through(2.8).See further remarks in that direction in Section 4 below.

Proof Step 1(Bounds)The energy equality immediately implies that,for some C>0 and every t∈[0,T],

Let Ω′⊆ RNbe open bounded such that Ω ∪ Γd= Ω ∩ Ω′.We extend(uε(t),eε(t),pε(t))toΩ′by setting

Clearly

By a generalized version of Helly’s theorem(see[7,Theorem 3.2]),there exists a subsequence,not relabeled,such that,for every t∈[0,T],

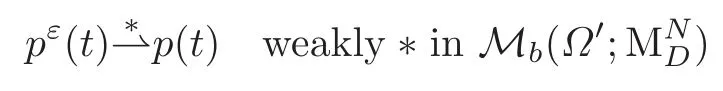
for someFor every t∈ [0,T],there exists a further subsequence{εt}such that

and,appealing to Korn’s inequality in BD,

for some u(t) ∈ BD(Ω′)with

Clearly u(t)=w(t),e(t)=Ew(t)and p(t)=0 on Ω′ Ω,so that we deduce

By restricting(u(t),e(t))to Ω and p(t)to Ω ∪ Γd,we get

with

Step 2(Stresses)Set t∈[0,T].Since

we deduce,using the balance equations in Remark 2.4,that

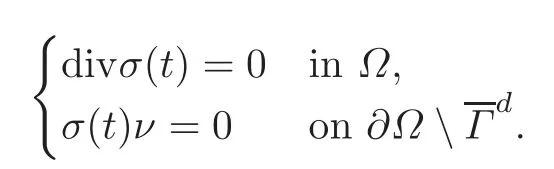
Concerning the stress constraint,the stress constraint in Remark 2.4 implies that

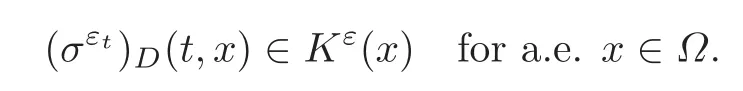
Since ϕε≡ 1 if dist(x,Γ)≥ ε,for ε small enough,the previous constraint reduces to

on any A⊂⊂Ωi.Since Kiis convex and closed,we conclude that

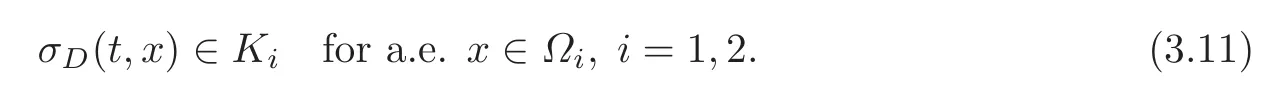
Now,on Γ S,by the definition of Kε,so that,in particular,

for some constant C>0.But,as detailed earlier in Subsection 1.2,since ΓS is a C2-hypersurface,is uniquely defined as the distributionon Γ S.That distribution converges to σD(t)ν− (σD(t)ν ·ν)ν on Γ S.But the latter is precisely[σD(t)ν]τ.

Because of the bound(3.12),we conclude that

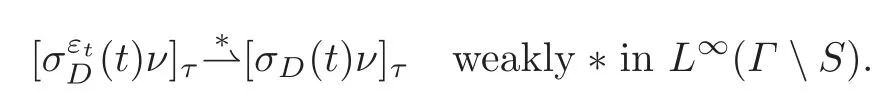
Since the weak-∗ limits of sequences of elements with values in[K3ν]τremain there in view of the convex and closed character of that set,we finally obtain that

Step 3(Global Stability)Set t∈[0,T].In view of(3.11)and(3.13),an argument identical to that of[5,Proposition 3.9]would demonstrate that,for every(v,η,q)∈ A(0),

Thanks to the admissibility of∂⌊∂ΩΓd,we can compute the masses and we obtain,in view of(2.2)(with f≡g≡0),

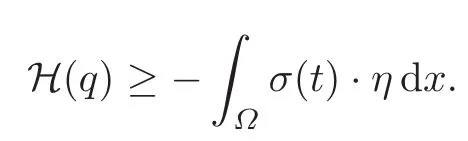
The previous inequality immediately implies global stability by convexity of the quadratic form Q(e).In particular,as demonstrated in[5,Remark 2.6],(u(t),e(t))is uniquely determined by p(t),so that the convergences in(3.10)hold without passing to a t-dependent subsequence.

Step 4(Lower Semi-continuity of the Dissipations)We argue at fixed t∈[0,T].Set

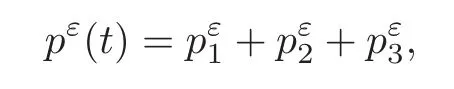
where,for i=1,2,

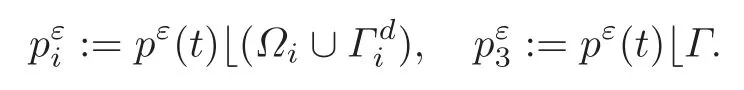
We can assume that,up to a(t-dependent)subsequence,

for i=1,3.Clearly,

with supp(pi)⊆ Ωi∪Γ ∪∪S′and supp(p3)⊆ Γ,so that,in particular,

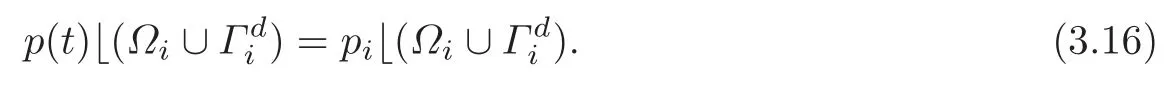
Further,according to[5,Lemma 5.1],for i=1,2,

where ν is the normal to Γ pointing towards Ω2, λiis a finite positive measure supported on Γ S and aiis a Borel function on Γ S with ai⊥ ν λi-a.e.on Γ S.

Now,as far asis concerned,we have

whereandare the traces of uεon Γ coming from Ω2and Ω1,respectively.Sinceis a bounded measure on Γ,we immediately conclude that,for some C>0,

so that,up to a subsequence that will not be relabeled,

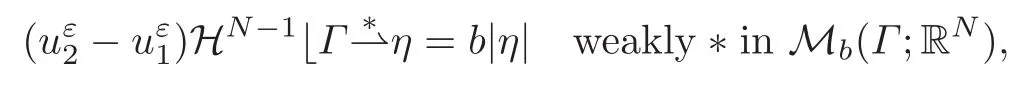
where b is the Borel Radon-Nikodym derivative of η with respect to its variation measure|η|.Since x 7→ ν(x)is continuous on Γ S,we deduce that

Recalling(3.17)–(3.18)and taking into account that p does not charge sets of HN−1-measure 0 while HN−1(S)=0,we conclude that,in particular,

where ζ:= λ1+ λ2+|η|and c is a suitable Borel function on Γ.

Fix η >0.In view of(3.5)–(3.6),a direct application of Reshetnyak’s lower-semi-continuity theorem(see,e.g.,[2,Theorem 2.38])yields,for i=1,2,

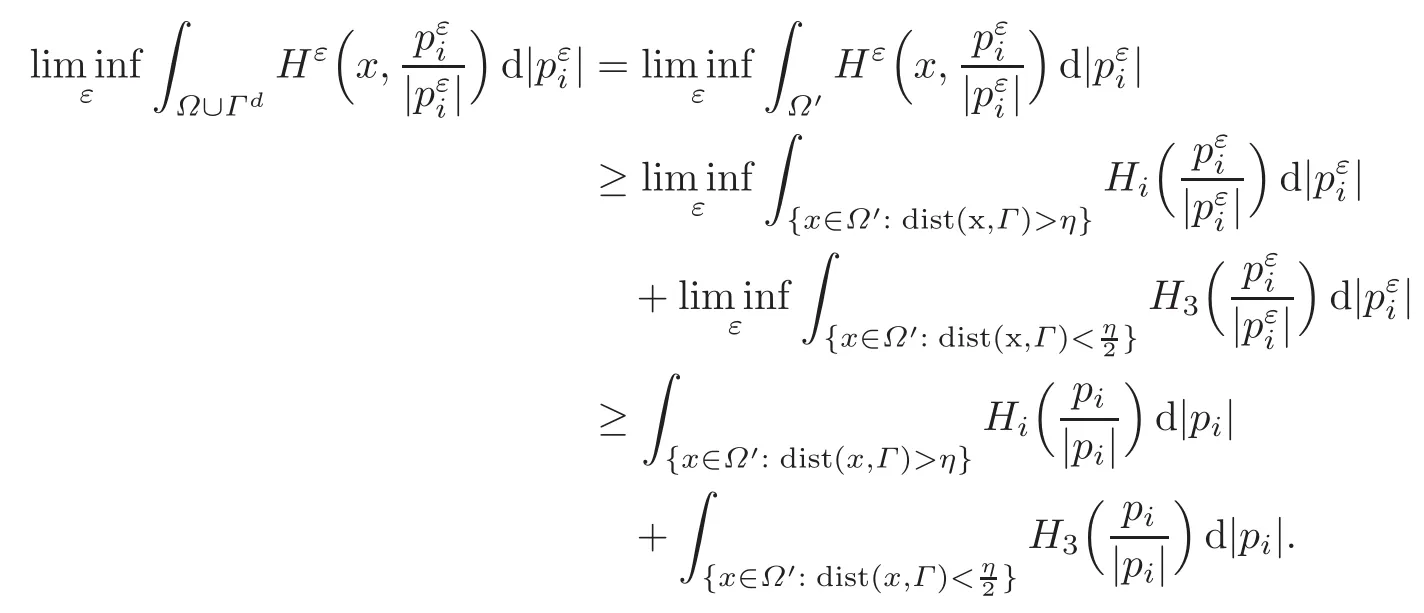
Letting η0 in the previous inequality and recalling(3.17)permit us to conclude that,for i=1,2,

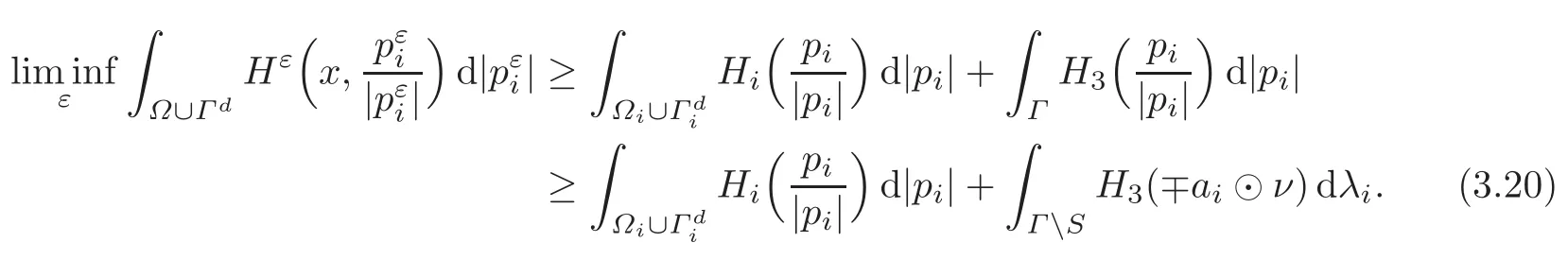
Further,a second application of Reshetnyak’s lower-semi-continuity theorem and(3.18)imply that

Collecting(3.20)–(3.21),we obtain

The sub-additive character of H3,(3.16)and(3.19)finally imply that

which establishes that

Step 5(Energy Equality)For every t∈[0,T],using(3.22),we get

Above,the last equality is obtained by dominated convergence and the last inequality is a consequence of the global stability of(u(t),e(t),p(t))∈A(w(t))proved in Step 3(see the end of the proof of[5,Theorem 2.7,after the equation(2.29)]).

We conclude that the energy equality holds,so that t 7→(u(t),e(t),p(t))is a quasi-static evolution for the two-phase+interface case according to Definition 2.3 and Remark 2.2.Moreover,the previous inequalities entail that

from which we infer

Thus in particular,

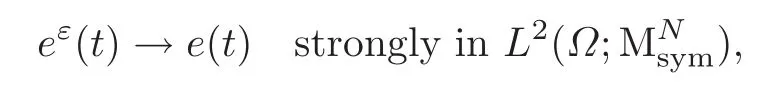
which concludes the proof.

4 Remarks

In this last section,we put forth various short remarks concerning the evolution obtained in Theorem 3.1.

Interfacial Stress AdmissibilityIn the course of proving Theorem 3.1,we established(see(3.13))that

Flow RuleAny solution of the quasi-static evolution given in Theorem 3.1 satisfies a flow rule as detailed in the following.

Theorem 4.1(Flow Rule) Consider a C2-geometrically admissible multi-phase domain.Also assume the admissibility of∂⌊∂ΩΓd(see Definition 2.1).For a.e.t∈ [0,T],

Moroever,

where˙u1(t)and˙u2(t)are the traces on Γ of the restrictions of˙u(t)to Ω1and Ω2,respectively,assuming that ν points from Ω1to Ω2,and wheredenotes the normal cone – a cone of vectors – to[K3ν(x)]τat a vector ζ⊥ ν(x).

Finally,there exists[σD(t)ν]τsuch that,for HN−1-a.e.

The proof will not be given here.It follows verbatim from that of[5,Propositions 3.9,3.11,Theorem 3.13].

Note that,in the pure two-phase case,the interfacial flow rule is different.In lieu of(4.2),one has,according to[5,Theorem 3.13],

So the interfacial effect due to the presence of the vanishing layer is felt in the admissibility rule(4.1),as well as in the flow rule(4.2).

Uniqueness of the StressIt can be established(see,e.g.,[5,Remark 2.6])that the Cauchy stress

is uniquely determined by the initial conditions.Consequently,any quasi-static evolution for the two-phase+interface case will be such that

whereas the balance equations(see Remark 2.4)and the stress admissibility constraints on each phase only permit us to assert a priori that

DissipationIn order to secure the lower semi-continuity of the dissipations in the fourth step of the proof of Theorem 3.1,we had to assume that K3⊂ K1∩K2,so that,correspondingly,H3(ξ) ≤ Hi(ξ),i=1,2.Barring this,the limit process fails.

A direct proof of the existence of an energetic quasi-static evolution for a two-phase+interface evolution could be produced in the spirit of that of[5,Theorem 2.7].The main hurdle,that is,the lower semi-continuous character of the dissipation H defined in(3.9),would become impossible to prove whenever K3is not a subset of K1∩K2.

Although,as stated above,one can prove directly the existence of an energetic quasi-static evolution for a two-phase+interface evolution,two results cannot be achieved through such a direct proof:The interfacial stress condition(4.1)and the interfacial flow rule(4.2).The approximation process devised in Section 3 is instrumental in deriving(4.1)from which(4.2)can then be obtained as in the proof of Theorem 4.1.

So,any elasto-plastic model for a two-phase+interface model will have a dissipation on the interface Γ which is less than that of the pure two-phase case,and correspondingly,a set of admissible stresses on the interface that is smaller than K1∩K2.Thus,the pure two-phase case can be seen as the maximally dissipative interfacial model compatible with the bulk dissipations.

[1]Ambrosio,L.,Coscia,A.and Dal Maso,G.,Fine properties of functions with bounded deformations,Arch.Rat.Mech.Anal.,139,1997,201–238.

[2]Ambrosio,L.,Fusco,N.and Pallara,D.,Functions of Bounded Variation and Free Discontinuity Problems,Oxford University Press,Oxford,2000.

[3]Dal Maso,G.,DeSimone,A.and Mora,M.G.,Quasistatic evolution problems for linearly elastic-perfectly plastic materials,Arch.Ration.Mech.Anal.,180(2),2006,237–291.

[4]Evans,L.C.and Gariepy,R.F.,Measure theory and fine properties of functions,CRC Press,Boca Raton,FL,1992.

[5]Francfort,G.A.and Giacomini,A.,Small-strain heterogeneous elastoplasticity revisited,Comm.Pure Appl.Math.,65(9),2012,1185–1241.

[6]Kohn,R.V.and Temam,R.,Dual spaces of stresses and strains,with applications to Hencky plasticity,Appl.Math.Optim.,10(1),1983,1–35.

[7]Mainik,A.and Mielke,A.,Existence results for energetic models for rate-independent systems,Calc.Var.Partial Differential Equations,22(1),2005,73–99.

[8]Mielke,A.,Evolution of rate-independent systems,Evolutionary Equations.Vol.II,Handb.Diff er.Equ.,Dafermos,A.and Feireisl,E.(eds.),Elsevier,North-Holland,Amsterdam,2005,461–559.

[9]Solombrino,F.,Quasistatic evolution problems for nonhomogeneous elastic plastic materials,J.Convex Anal.,16(1),1979,89–119.

[10]Suquet,P.M.,Un espace fonctionnel pour les équations de la plasticité,Ann.Fac.Sci.Toulouse Math.(5),1(1),1979,77–87.

[11]Suquet,P.M.,Sur les équations de la plasticité:existence et régularité des solutions,J.Mécanique,20(1),1981,3–39.

[12]Temam,R.,Problèmes mathématiques en plasticité,Méthodes Mathématiques de l’Informatique[Mathematical Methods of Information Science],Vol.12,Gauthier-Villars,Montrouge,1983.