Thermal Creep Flow for the Boltzmann Equation

Feimin HUANG

(In Honor of the Scientific Contributions of Professor Luc Tartar)

1 Introduction

The fundamental equation in statistical physics for rarefied gas is the famous Boltzmann equation which gives a description of the time evolution of particle distribution.Even though it has close relation to the classical systems in fluid dynamics,it provides more information on the microscopic level so that it describes some phenomena which can not be modeled by using the classical Euler and Navier-Stokes equations.This kind of interesting phenomena,called the “ghost effect”,such as the thermal creep flow in a rarefied gas,was known since the time of Maxwell.The mathematical formulation and numerical computation on the basis of kinetic equation have been studied since the 1960s.

There was tremendous progress made on the mathematical theories for the Boltzmann equation,such as the global existence of weak(renormalized)solutions for large data(see[10])and classical solutions as small perturbations of the equilibrium states(Maxwellian)(see[26]),fluid dynamic limits(see[2–3,5,11–12,14,19,21–22,27,35–37]and the references therein),etc.Among them,the classical works of Hilbert,Chapman-Enskog reveal the close relation of the Boltzmann equation to the classical systems of fluid dynamics through asymptotic expansions with respect to the Knudsen number which is assumed to be small.In some physical situations,the studies of both Sone and his group,and Kogan showed that the classical systems,such as the Euler and Navier-Stokes equations,are not enough to describe the behavior of the macroscopic components in the solution to the Boltzmann equation.In addition to some interesting experiments,Sone and his group verified this kind of phenomena mainly by using asymptotic expansions and numerical computations.

More precisely,the non-dimensional Boltzmann equation takes the form

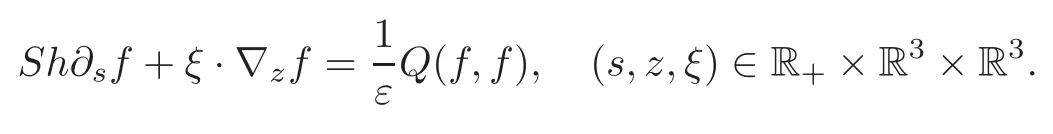
Here f(s,z,ξ)≥ 0 is the distribution function of particles,and Q(f,f)is the collision operator which is a non-local bilinear operator in the velocity variable with a kernel determined by the physics of particle interaction.There are two parameters Sh and ε in the above equation which are called Strouhal and Knudsen numbers,respectively.Their product Sh·ε is 2√π times the ratio of the mean free time to the reference time.And the non-dimensional parameters ε and Sh·ε not only characterize the different effects coming from the molecular collisions,but also give the weight of the spatial and temporal derivatives with respect to the collision operator.

As mentioned,the relation between the Boltzmann equation and the classical systems of fluid dynamics was presented in the Hilbert and Chapman-Enskog expansions when Sh=1 and ε is small.And the justification of this kind of relations was raised in the Hilbert’s sixth problem,i.e.,the “mathematical treatment of the axioms of physics”,in his famous lecture“Mathematical Problems” at ICM in 1900.

On the other hand,there are some phenomena described by the Boltzmann equation,for which the time evolution of the macroscopic components is not governed by the classical fluid dynamic systems.This happens,for example,when the parameters Sh and ε as well as the macroscopic velocity are small while the density and temperature are of the order 1,such as the thermal creep flow phenomenon.Unlike the Poiseuille flow induced by the gradient of pressure and described by the Navier-Stokes equations,the thermal creep flow is induced by the gradient of the wall temperature and can not be modeled by the Navier-Stokes equations.There were a lot of studies on this kind of phenomena and most of the results are mainly built on the asymptotic expansions and numerical computations(see[3,30]and the references therein).Recently,Chen-Chen-Liu-Sone[8]first gave a rigorous mathematical analysis in which the thermal creep flow is studied for the stationary linearized Boltzmann equation.However,the time evolutionary and nonlinear problems about this kind of phenomena provide a lot of challenging mathematical topics remaining unsolved.

As for the thermal creep flow,we assume that both the Strouhal number and the macroscopic velocity(i.e.,flow velocity)are of the order of ε,and rewrite the Boltzmann equation under the following scalings:

Hence,the solution to the Boltzmann equation has the following macroscopic and microscopic decompositions(see[3]):

Here M[ρ,εu,θ]is the local Maxwellian and G is the microscopic component.Moreover,the local Maxwellian M[ρ,εu,θ]is defined by the five conserved quantities,that is,the mass density ρ(s,z),the momentum density m(s,z)= ερ(s,z)u(s,z)and the energy densitygiven by

as

Here the collision invariants ψα(ξ)are given by(see[4])

satisfying

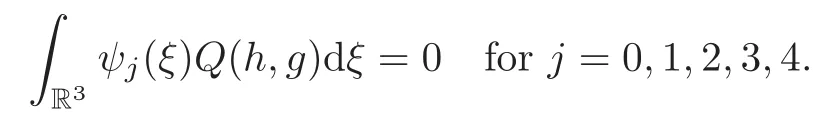
As usual,θ(s,z)is the temperature related to the internal energy E byRθ with R being the gas constant,and εu(s,z)is the flow velocity.Here u is the scaled flow velocity which appears in the equations for the macroscopic variables ρ and θ.

When ε→ 0,(1.1)implies that the solution converges to M[ρ,0,θ]formally.Mathematically,it means that the equations governing the time evolution of the functions ρ and θ depend actually on the scaled velocity u even though the macroscopic velocity tends to zero.An interesting phenomenon is that the flow moves from the low temperature to the high one when the gas is very rarif i ed,while on the Euler or Navier-Stokes level,the flow moves from the high temperature to the low one,which is well-known in heat flow.Therefore,the resulting system of equations for these macroscopic variables, ρ,u and θ,is not given by either the classical Euler or Navier-Stokes equations.Indeed,by expanding the variables in the power of ε and letting(ρ0,u0,θ0)be the leading order of the variables(ρ,u,θ),Bardos-Levermore-Ukai-Yang[3]derived the following system for(ρ0,u0,θ0)which is the same as that obtained by Sone using Hilbert expansion:

where P∗is an unknown scalar pressure while

I is the identity matrix,and γj(θ)(j=1,2,3,4)are positive functions of θ>0 whose explicit formulas can be found in the book by Sone[32].(1.4)is now called the ghost effect system.Notice that(1.4)1means that

the pressure p0=Rρ0θ0is a function of timebut not of z.

Clearly,the function p0is given by the boundary conditions or the far fields in the z-space but not by the initial condition.Recently,Levermore,Sun and Trivisa[25]established the local well-posedness result for the Cauchy problem of the ghost effect system(1.4).However,it is not clear whether there exists the ghost effect phenomenon in the solutions obtained in[25]or not.

In this note,we will consider the Boltzmann equation with slab symmetry so that the space dimension reduces to one.We first construct explicit solutionsof(1.4)in which the flow moves from the low temperature to the high one(see Figures 1–2 below).These solutions precisely show the thermal creep flow phenomenon for(1.4).

Figure 1 θ− < θ+

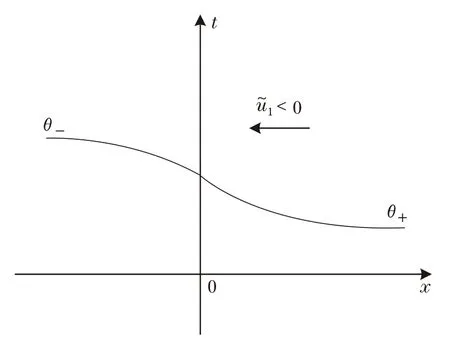
Figure 2 θ− > θ+

Furthermore,the expansion in the Knudsen number of the Boltzmann equation,as for the thermal creep flow,is justified mathematically,that is,(1.4)is indeed a good approximation for the ghost effect of the Boltzmann equation.Then we further show that when the Knudsen number is sufficiently small,the macroscopic components in the solutions of the nonlinear Boltzmann equation also have the thermal creep flow phenomenon in a special setting by stability analysis,based on the above special solutions as background states.The precise statement of the main results will be given in Theorem 2.1 in the next section.

2 Construction of the Profile and the Main Theorem

Since the profile studied is in one-space dimension,we consider the scaled Boltzmann equation with “slab symmetry”

where f(z,s,ξ)represents the distributional density of particles at space-time(z,s)with velocity ξ.For monatomic gas,the rotational invariance of the molecule leads to the collision operator Q(f,f)as a bilinear collision operator in the form(see[4])

with θ being the angle between the relative velocity and the unit vector Ω.Here={Ω ∈S2:(ξ− ξ∗)·Ω ≥ 0}.The conservation of momentum and energy gives the following relation between velocities before and after collision:

In this paper,we consider the Boltzmann equation for the hard sphere model,for simplicity,i.e.,the collision kernel B(|ξ− ξ∗|,θ)takes the form

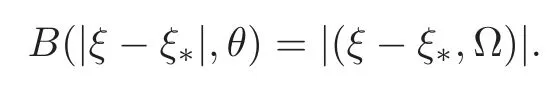
Using the macroscopic and microscopic decompositions as in[3],or in[26,28],the Boltzmann equation(2.1)is equivalent to the following system(see[20]for details):

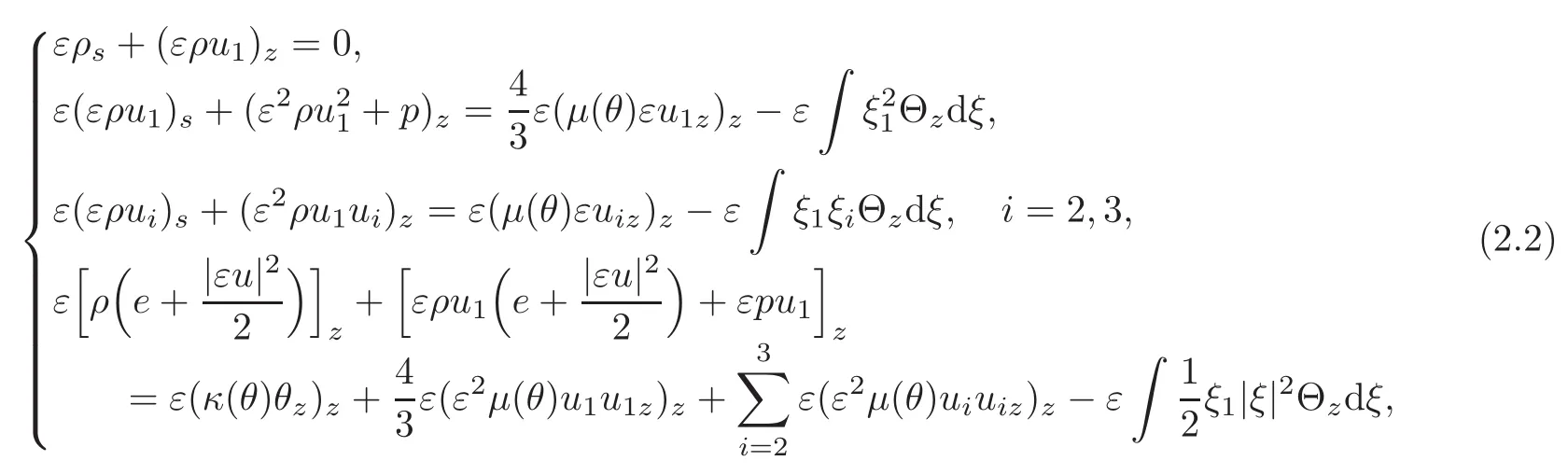
together with the following equation for the non-fluid component G:

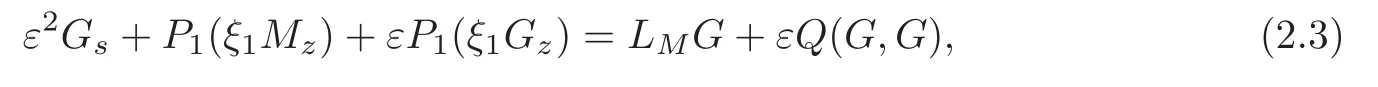
where

Here LMis the linearized operator of the collision operator with respect to the local Maxwellian M,

In the above presentation,we normalize the gas constant R to befor simplicity so thatandNotice also that the viscosity coefficient µ(θ)>0 and the heat conductivity coefficient κ(θ)>0 are smooth functions of the temperature θ.And the following relation holds between these two functions(see[7,15]):

after takingIt should be pointed out that(2.4)is crucially used in the following analysis.In fact,in our analysis,it is required that

for all θ under consideration.By(2.4),it is known that the above condition holds provided that the variation of the temperature is suitably small.

Note that with slab symmetry,(1.4)in one-space dimension reads

where P∗is an unknown function and

With slab symmetry,on the macroscopic level,it is more convenient to rewrite the system and the equation by using the Lagrangian coordinates as in the study of conservation laws,that is to consider the coordinate transformation as follows:

(2.1)in the Lagrangian coordinates becomes

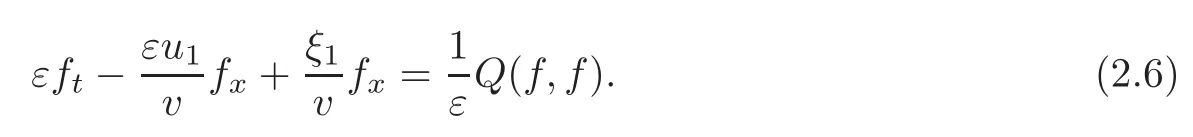
Moreover,(2.2)and(2.3)take the forms

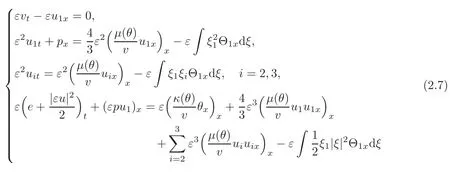
and

respectively,with

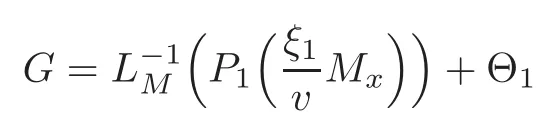
and

respectively.

On the other hand,(1.4)derived by Bardos-Levermore-Ukai-Yang[3]becomes

2.1 Construction of the profile

We will construct the profile with the thermal creep flow in this subsection.We first consider(2.10)and try to find a special solution in which the thermal creep flow is shown as in Figures 1–2 in the previous section.From(2.10)1,we observe that θ ≡v andif we assume,without loss of generality,that the boundary conditions at the far fields satisfy

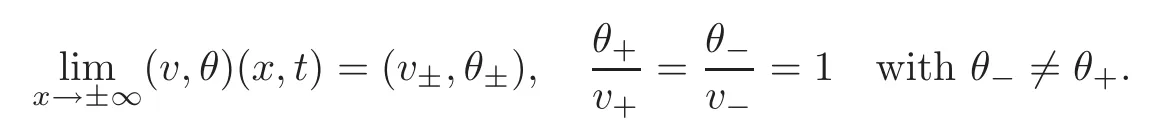
Then(2.10)4is rewritten as

Substituting(2.10)2into(2.11)and noting that v≡ θ,we get the following scalar nonlinear diffusion equation:

From[1]and[9],it is known that the nonlinear diffusion equation(2.12)admits a self-similar solutionwith η=satisfying the boundary conditions(±∞,t)=θ±.Let δ=|θ+− θ−|,and thenhas the property that

Define

and then from(2.12),it can be checked thatsatisfies(2.10)as

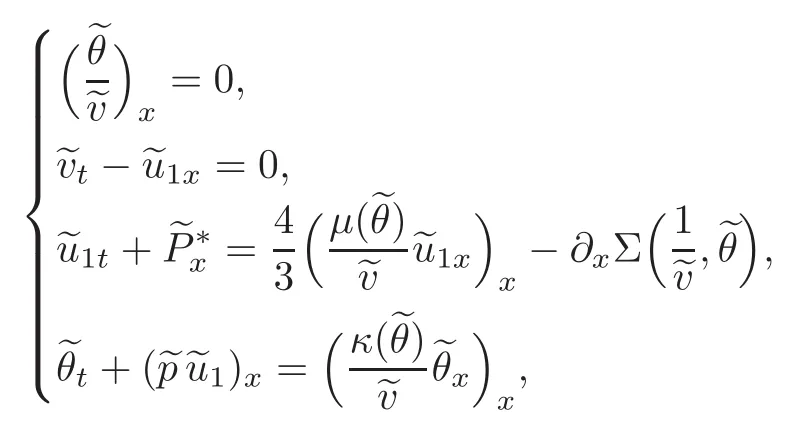
whereThat is,is a special solution of the ghost effect system(2.10).

Remark 2.1If θ−<θ+,thenthat is,the flow moves from the low temperature to the high one(see Figure 1).The case θ−> θ+also has the same phenomenon.

Remark 2.2The construction of the profileis motivated by the one of the viscous contact wave of compressible Navier-Stokes equations(see[18,23–24]).The viscous contact wave is used to approximate the contact discontinuity for compressible Euler equations and its pressure keeps constant.

For the Boltzmann equation,if we use the profilethen some non-t-integrable error terms with bad ε-decay rates,coming from the non-fluid component,exist for the integrated equation for(see Subsection 2.2).Therefore,we need to construct a profilefor the Boltzmann equation,based on the explicit solutionsof the ghost effect system(2.10).For this,we require that the approximate pressure p satisf i y

Motivated by[24]for the Boltzmann equation,we first notice that the principle part of the non-fluid component in the solution G and part of Θ1defined in(2.9)are given by

and

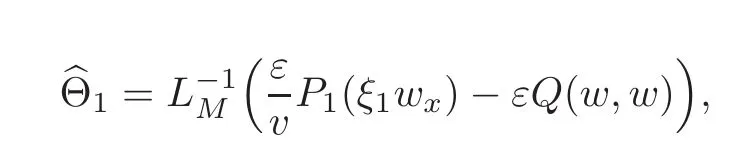
respectively.To distinguish the leading term coming from the non-fluid component,we rewrite the Boltzmann equation(2.7)as

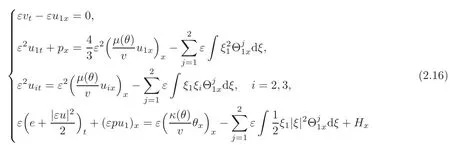
with

where

satisfy

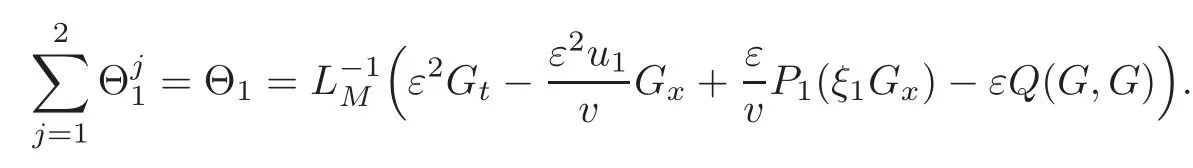
Here,the functionis the profile to be constructed.

Since the velocity εu decays faster than(v,θ)in time,the leading part in the energy equation(2.16)4is

By the definition of,it holds that

where the coefficients f1j(j=1,2,3,4)are smooth functions of(v,εu,θ).By(2.15),it is expected that the profilefor the Boltzmann equation satisfiesThus,by choosing only the leading term in(2.19),we have

where a(θ)is given in(2.12).Thus the leading part of(2.21)is the nonlinear diffusion equation(2.12)and an explicit solutionis given with the boundary conditions

To include more microscopic effects,let the profilewhere θnf(x,t)represents the part of the nonlinear diffusion wave coming from the non-fluid component and not appearing on the macroscopic level.Moreover,the term θnf(x,t)in the formis from N1in(2.21).Note that θnf(x,t)decays faster thanso that it can be viewed as a perturbation around the Navier-Stokes profileTo construct θnf(x,t),we linearize the equation(2.21)aroundand keep only the linear terms.This leads to a linear equation for θnf(x,t)from(2.21)as follows:

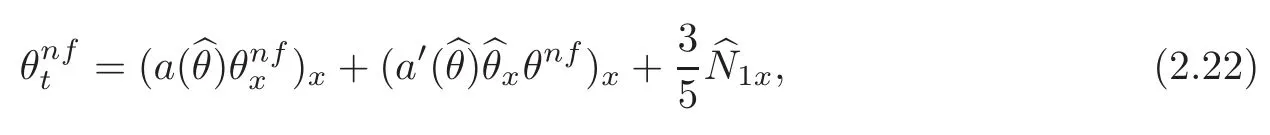
wherewithLet

and then integrating(2.22)with respect to x yields that

Note thattakes the formand satisfies the property

We can check that there exists a self-similar solution g1(η),for(2.23)with the boundary condition g1(−∞,t)=0,g1(+∞,t)= δ1.Here δ1satisfies 0< δ1< δ.It is worthy of pointing out that even though the function g1(x,t)depends on the constant δ1,θnf(x,t)=g1x(x,t)→ 0 as x → ±∞.That is,the choice of the constant δ1has no influence on the ansantz as long as|δ1|< δ.From now on,we fix δ1so that the function g1(x,t)is uniquely determined and its derivative g1x=θnfhas the property

Now we follow the same procedure to construct the second and third components of the velocity of the ghost profile denoted by(i=2,3).Similarly,the leading part of the equation for εuicoming from(2.16)is

For i=2,3,we have

with smooth functions fij(i=2,3,j=1,2,3,4).Notice that the symbols Niand Fi(i=2,3),used here are for the convenience of notations.

From(2.24)–(2.25),we expect that the profile(x,t)takes the formand satisfies the following linear equation:

wherei=2,3,j=1,2,3,4.

Denote

and then integrating(2.26)with respect to x,we have

For givenwe can check that there exists a self-similar solution gi(η)withand the boundary conditions gi(−∞,t)=0,gi(+∞,t)= δi,where δisatisfies 0< δi< δ.As we explained before,the choice of the constant δiis not important to our result.From(2.13),we fi x δiso that the function gi(x,t)is uniquely determined and the derivativehas the following property:

where b(θ±)=max

In summary,we can define the profile with the ghost effectfor the Boltzmann equation as follows.To satisfy the conservation of mass,we need

By lettingwe have

However,by plugging(2.28)into the momentum equation of(2.16),we have a non-conservative term containingTo avoid this,we define

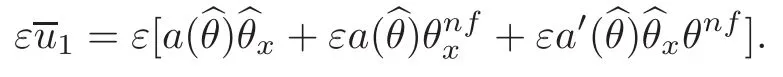
Similarly,to avoid the non-conservative termin the energy equation,we set

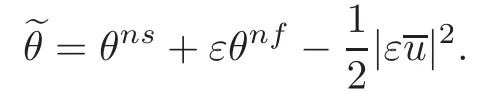
Therefore,the profileis finally defined as

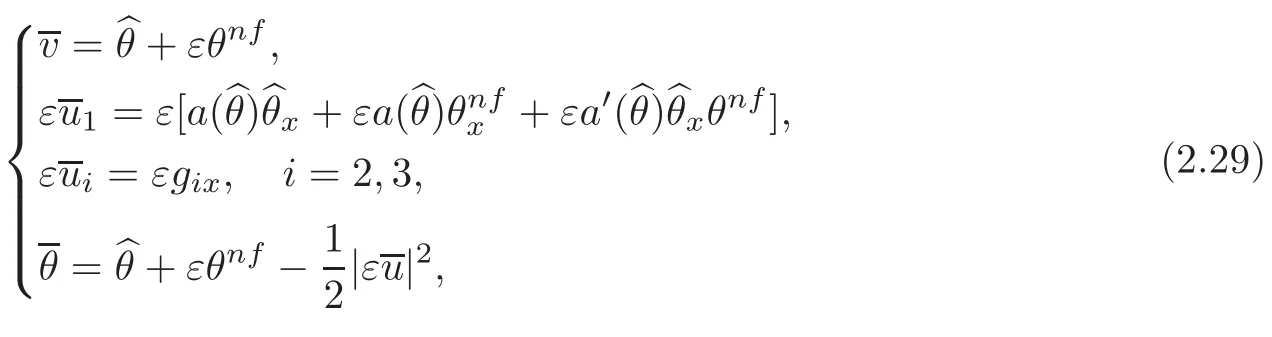
whereis given by(2.12),θnfby(2.22)and gi(i=2,3)by(2.27).Then a direct but tedious computation shows that

where

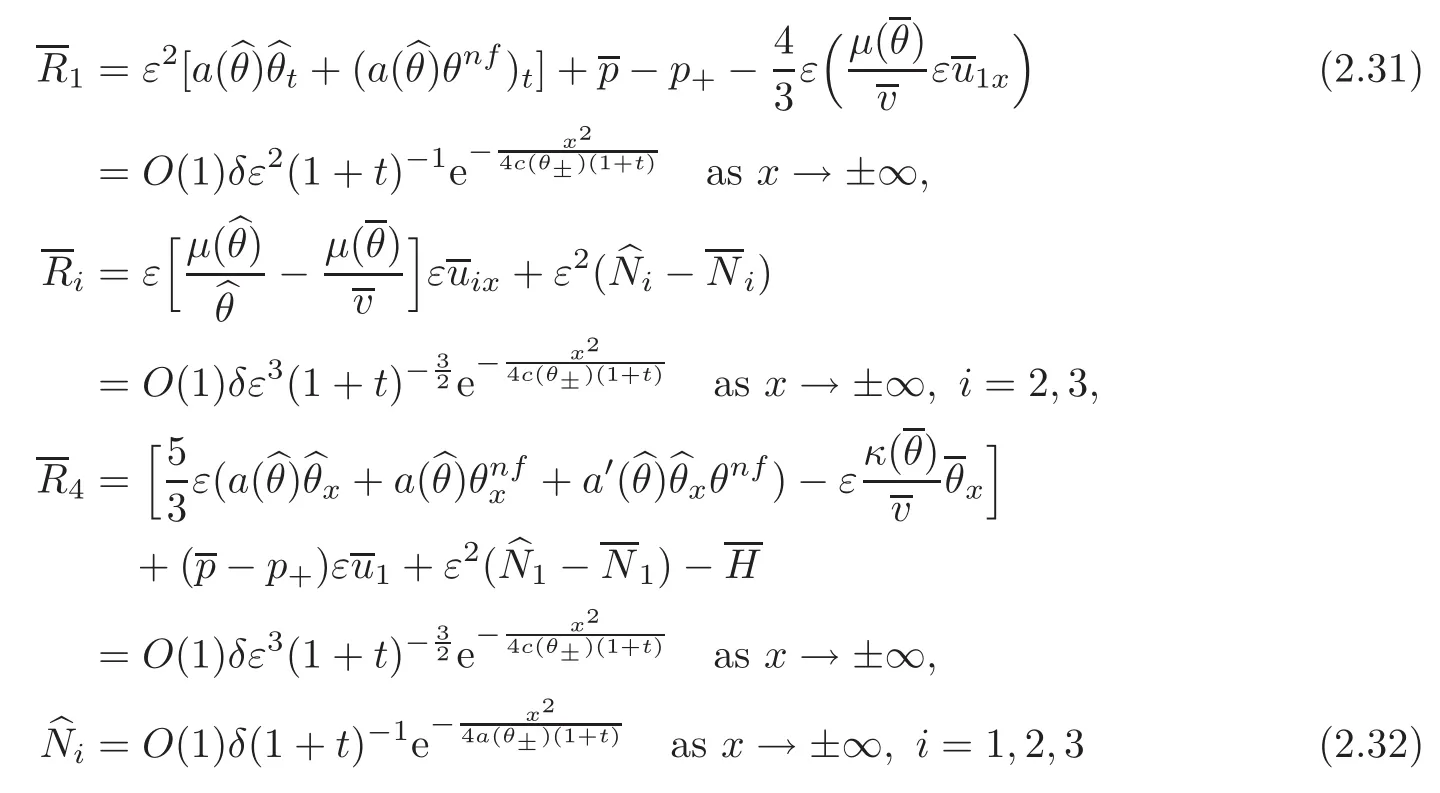
with c(θ±)=max{a(θ±),(i=1,2,3)andare the corresponding functions defined in(2.18),(2.20)and(2.25)by substituting the variable(v,εu,θ)by the profileIt is worthy of pointing out that the decay rate of(i=2,3,4)is of orderFurthermore,even though the decay rate ofis still ε2(1+t)−1,it is sufficient to give the desired a priori estimates through a subtle analysis coming from the intrinsic dissipation mechanism in the momentum equations.

Define

and

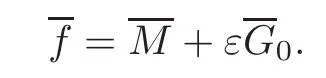
Then from(2.30)we have

where

and

Remark 2.3From the definition ofin(2.14)and the definition ofin(2.29),it holds that

which implies that the ansantzapproximates the solutionto the ghosteffect system(2.10)as ε is small.

2.2 The main result

Now we consider(2.7)–(2.8)with the initial data

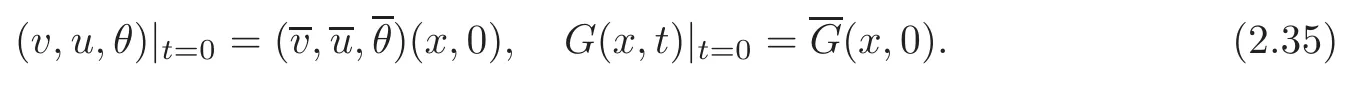
We have the following theorem.

Theorem 2.1Let(x,t)be the profile defined in(2.29)with strength δ=|θ+− θ−|.Then there exist small positive constants δ0and ε0and a global Maxwellian M∗=M[v∗,u∗,θ∗],such that when δ≤ δ0and ε≤ ε0,the Cauchy problem(2.7)–(2.8)with the initial data(2.35)has a unique global solution(v,u,θ,G)satisfying,for any sufficiently small but fixed positive constant ϑ>0,

which implies that

where C is a positive constant independent of ε and δ.

ProofThe detailed proof of Theorem 2.1 can be found in my recent paper[20],jointly with Wang and Yang.

Remark 2.4The initial data(2.35)is chosen specially in Theorem 2.1.It is noted that Theorem 2.1 is also true if the initial data belongs to some sets depending on ε.

The following result is about the justification of the expansion in the Knudsen number of the Boltzmann equation(2.1)as for the thermal creep flow.

Corollary 2.1Under the conditions of Theorem 2.1,from(2.34)and(2.37),it holds that

that is,the fluid part(v,u1,θ)of the solution of(2.1)converges to the solutionof(2.10)in the sense of(2.38)as the Knudsen number ε tends to zero.As in Remark 2.1,the flowis driven byas shown in Figures 1–2,and therefore we justify the expansion in the Knudsen number of the Boltzmann equation as for the thermal creep flow in a mathematical setting rigorously.

From the definition ofwithin(2.12)–(2.13),it can be seen thatis monotonic.To be definite and without loss of generality,let us assume that θ−<θ+,that is,bθ is monotonically increasing.Then there exists η0>0 such that

where cη0is a positive constant depending on η0.

Corollary 2.2Under the conditions of Theorem 2.1,for any fixed η0>0,there exists a small positive constant ε1= ε1(η0) ≤ ε0,such that if ε≤ ε1,then it follows from(2.37)and(2.39)that

where C1is a suitably large positive constant depending only on θ±.In particular,(2.40)implies that the flow is driven by the gradient of the temperature,that is,the flow speed u1is proportional to the temperature gradient θxin the sense of(2.40)on the region increasing with the time rate

[1]Atkinson,F.V.and Peletier,L.A.,Similarity solutions of the nonlinear diffusion equation,Arch.Rat.Mech.Anal.,54,1974,373–392.

[2]Bardos,C.,Golse,F.and Levermore,D.,Fluid dynamic limits of kinetic equations,I,Formal derivations,J.Statis.Phys.,63,1991,323–344;II,Convergence proofs for the Boltzmann equation,Comm.Pure Appl.Math.,46,1993,667–753.

[3]Bardos,C.,Levermore,C.,Ukai,S.and Yang,T.,Kinetic equations:Fluid dynamical limits and viscous heating,Bull.Inst.Math.Acad.Sin.(N.S.),3,2008,1–49.

[4]Boltzmann,L.,Lectures on Gas Theory,translated by G.Stephen Brush,Dover Publications,New York,1964.

[5]Caf l isch,R.E.,The fluid dynamical limit of the nonlinear Boltzmann equation,Comm.Pure Appl.Math.,33,1980,491–508.

[6]Cercignani,C.,Illner,R.and Pulvirenti,M.,The Mathematical Theory of Dilute Gases,Springer-Verlag,Berlin,1994.

[7]Chapman,S.and Cowling,T.G.,The Mathematical Theory of Non-Uniform Gases,3rd edition,Cambridge University Press,Cambridge,1990.

[8]Chen,C.C.,Chen,I.K.,Liu,T.P.and Sone,Y.,Thermal transpiration for the linearized Boltzmann equation,Comm.Pure Appl.Math.,60(2),2007,147–163.

[9]Duyn,C.T.and Peletier,L.A.,A class of similarity solution of the nonlinear diffusion equation,Nonlinear Analysis,T.M.A.,1,1977,223–233.

[10]DiPerna,R.J.and Lions,P.L.,On the Cauchy problem for Boltzmann equations:Global existence and weak stability,Annals of Mathematics,130(2),1989,321–366.

[11]Esposito,R.and Pulvirenti,M.,From particle to fluids,Handbook of Mathematical Fluid Dynamics,Vol.III,North-Holland,Amsterdam,2004,1–82.

[12]Golse,F.,The Boltzmann equation and its hydrodynamic limits,evolutionary equations,Handb.Diff er.Equ.,Vol.II,Elsevier,North-Holland,Amsterdam,2005,159–301.

[13]Golse,F.,Perthame,B.and Sulem,C.,On a boundary layer problem for the nonlinear Boltzmann equation,Arch.Ration.Mech.Anal.,103,1986,81–96.

[14]Golse,F.and Saint-Raymond,L.,The incompressible Navier-Stokes limit of the Boltzmann equation for hard cutof fpotentials,J.Math.Pures Appl.,91,2009,508–552.

[15]Grad,H.,Asymptotic Theory of the Boltzmann Equation II,Raref i ed Gas Dynamics,J.A.Laurmann(ed.),Vol.1,Academic Press,New York,1963,26–59.

[16]Guo,Y.,The Boltzmann equation in the whole space,Indiana Univ.Math.J.,53,2004,1081–1094.

[17]Huang,F.M.,Li,J.and Matsumura,A.,Asymptotic stability of combination of viscous contact wave with rarefaction waves for one-dimensional compressible Navier-Stokes system,Arch.Rat.Mech.Anal.,197,2010,89–116.

[18]Huang,F.M.,Matsumura,A.and Xin,Z.P.,Stability of contact discontinuities for the 1-D compressible Navier-Stokes equations,Arch.Rat.Mech.Anal.,179,2005,55–77.

[19]Huang,F.M.,Wang,Y.,Wang,Y.and Yang,T.,The limit of the Boltzmann equation to the Euler equations for Riemann problems,SIAM J.Math.Anal.,45(3),2013,1741–1811.

[20]Huang,F.M.,Wang,Y.,Wang,Y.and Yang,T.,Justif i cation of diffusion limit for the Boltzmann equation with a non-trivial profile,submitted.

[21]Huang,F.M.,Wang,Y.and Yang,T.,Hydrodynamic limit of the Boltzmann equation with contact discontinuities,Comm.Math.Phy.,295,2010,293–326.

[22]Huang,F.M.,Wang,Y.and Yang,T.,Fluid dynamic limit to the Riemann solutions of Euler equations:I,Superposition of rarefaction waves and contact discontinuity,Kinet.Relat.Models,3,2010,685–728.

[23]Huang,F.M.,Xin,Z.P.and Yang,T.,Contact discontinuity with general perturbations for gas motions,Adv.Math.,219(4),2008,1246–1297.

[24]Huang,F.M.and Yang,T.,Stability of contact discontinuity for the Boltzmann equation,J.Differential Equations,229,2006,698–742.

[25]Levermore,C.D.,Sun,W.R.and Trivisa,K.,Local well-posedness of a ghost effect system,to appear.

[26]Liu,T.,Yang,T.and Yu,S.H.,Energy method for the Boltzmann equation,Physica D,188,2004,178–192.

[27]Liu,T.,Yang,T.,Yu,S.H.and Zhao,H.J.,Nonlinear stability of rarefaction waves for the Boltzmann equation,Arch.Rat.Mech.Anal.,181,2006,333–371.

[28]Liu,T.and Yu,S.H.,Boltzmann equation:Micro-macro decompositions and positivity of shock profiles,Commun.Math.Phys.,246,2004,133–179.

[29]Maxwell,J.C.,On the dynamical theory of gases,Phil.Trans.Roy.Soc.London,157,1866,49–88.

[30]Sone,Y.,Asymptotic theory of a steady flow of rarefied gas past bodies for small Knudsen numbers,Advances in Kinetic Theory and Continuum Mechanics,Proceedings of a Symposium Held in Honor of Professor Henri Cabannes(Paris,July 6,1990),R.Gatignol and Soubbaramayer(eds.),Springer-Verlag,Berlin,1991,19–31.

[31]Sone,Y.,Kinetic Theory and Fluid Dynamics,Birkhäuser,Boston,2002.

[32]Sone,Y.,Molecular Gas Dynamics,Theory,Techniques,and Applications,Birkhäuser,Boston,2006.

[33]Ukai,S.,Solutions of the Boltzmann Equation,Pattern and Waves-Qualitative Analysis of Nonlinear Differential Equations,M.Mimura and T.Nishida(eds.),Studies of Mathematics and Its Applications,18,Kinokuniya-North-Holland,Tokyo,1986,37–96.

[34]Ukai,S.,The incompressible limit and the initial layer of the compressible Euler equation,J.Math.Kyoto Univ.,26,1986,323–331.

[35]Ukai,S.and Asano,K.,The Euler limit and initial layer of the Boltzmann equation,Hokkaido Math.J.,12,1983,311–332.

[36]Xin,Z.P.and Zeng,H.H.,Convergence to the rarefaction waves for the nonlinear Boltzmann equation and compressible Navier-Stokes equations,J.Diff.Eqs.,249,2010,827–871.

[37]Yu,S.H.,Hydrodynamic limits with shock waves of the Boltzmann equations,Commun.Pure Appl.Math.,58,2005,409–443.