Pressure Boundary Conditions for Blood Flows

Kirill P.GOSTAF Olivier PIRONNEAU

(In Honor of the Scientific Contributions of Professor Luc Tartar)

1 Introduction

Computational hemodynamics is a major research field with many applications to the human blood circulatory system(especially for heart diseases and aneurysms)leading to diagnostic tools and simulations of chirurgical treatments like stents(see[34])and by-passes(see[35]).

Since the pioneering work of Peskin[27]impressive progress was made both on the methodological side,namely the treatment of moving walls,cardiac muscles,etc.,and on the numerical side for efficient and stable discretizations of these fluid structure interaction problems.Some were presented in[13],mostly with methods on fixed domains after a change of variables(see[7,12,24]and the reference therein).For other methods like the fictitious domain and immersed boundary methods,the reader is referred to[2,26–27,36],among others.Level sets have not been as popular but they can also be used as in[5].

In this paper,we focus on geometries similar to aortic flows.Typically,a large artery like the aorta has a radius of 1cm and a length of 5 to 10 centimeters;the thickness of the aortic wall is around 0.1 cm;the heart pulse is about 1Hz and the pressure at the input boundary 6KPa.Knowing the density and viscosity,this fixes a typical speed for the blood.At such speed the flow is Newtonian,incompressible with a Reynolds number of a few thousand.

The aorta is surrounded by organs,so in all its generality the problem is very complex:Large displacement visco-elasticity deformable solid with contacts on the surrounding organs and fluidstructure interaction(FSI for short)with a flow modeled by the Navier-Stokes equations in a moving domain.

2 Modeling the Aortic Wall:The Surface Pressure Model

The modeling and simulations of solids having large displacements and contacts are difficult but not impossible(see[16–17]),and rubber tires in particular are modeled as such,but they are computationally very expensive and even more so in the context of blood flow(see the computations in[23]).

A hierarchy of approximations was proposed.First,replace large displacement nonlinear elasticity by small displacement linear elasticity(see[6]),then use shell models like Koiter’s as in[8,22],and finally assume that the displacementis normal to the aortic wall,

In such case,as shown in[24],Koiter’s model reduces to a scalar equation for η,

on the mean position Σ of the vessel’s wall,where h denotes its average thickness and ρsits density,T is the pre-stress tensor,needed because at rest the vessel is blown up by the blood like a balloon,C is a damping term,a,b are viscoelastic terms,and fsis the external normal force,i.e.,is the normal component of the normal stress at the surface of the solid.

The final approximation is to assume that[h,T,C,a]≪b which leads to the surface pressure model

where A is the vessel’s cross section,E is the Young modulus,and ξ is the Poisson coefficient.Some typical values(MKSA for short)are as follows:

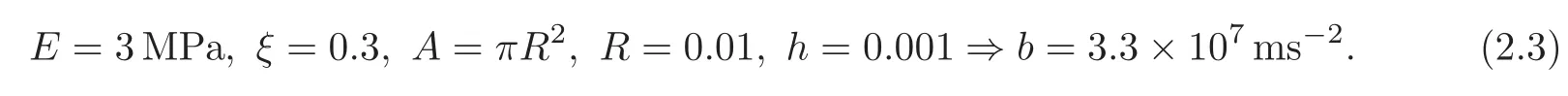
(2.2)assumes a circular cross section,but it can be extended to other shapes(see[24]).

3 Modeling Fluids with Given Boundary Pressure or Stress

For Newtonian incompressible fluids,pressure p and velocityare given by

where ρfis the density of the fluid,µ is the viscosity and σf= −pI+µ(∇u+∇uT)is the stress tensor.

Many boundary conditions were proposed for the artificial boundaries created by taking only a portion of the blood circulatory system(see[10,12,37]).

In this paper,the velocity and pressure are given at time t=0,the pressure is given on Γ(the inlet and the outlet)and the normal stress is given on Σ by the structure model for the compliant wall.Naturally,Γ ∪ Σ = ∂Ω.As the inlet and outlet are artificial boundaries,we assume that Γ is made of plane surfaces and the flow is normal to the inlet and outlet(the butcher cuts perpendicularly to the vessel),and the surface pressure model also implies normal velocity on Σ,

A variational formulation is obtained by multiplying the first equation in(3.1)byand the second one byThen for alland allsuch that×n=0 on∂Ω,

whereIndeed,when Γ is f l at,

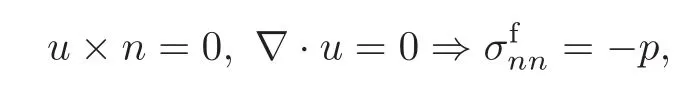
because the tangential derivatives of u are zero.

Such pressure boundary conditions were studied in[1,29](see also[28]).Existence and uniqueness may be proved as in the classical case following[15],and finite element approximations have been studied in[25],but there are some difficulties.First,because of the condition u × n|∂Ω=0,one aught to use the curl-curl formulation,

Recovery of the strong form of the Navier-Stokes equations when regularity allows makes use of the following formula(see[3–4]):For all u,v ∈ H2(Ω)with either u×n=v× n=0 or u·n=v·n=0 on ∂Ω,

with b(u,v)=Furthermore,if∂Ω is piecewise plane,then

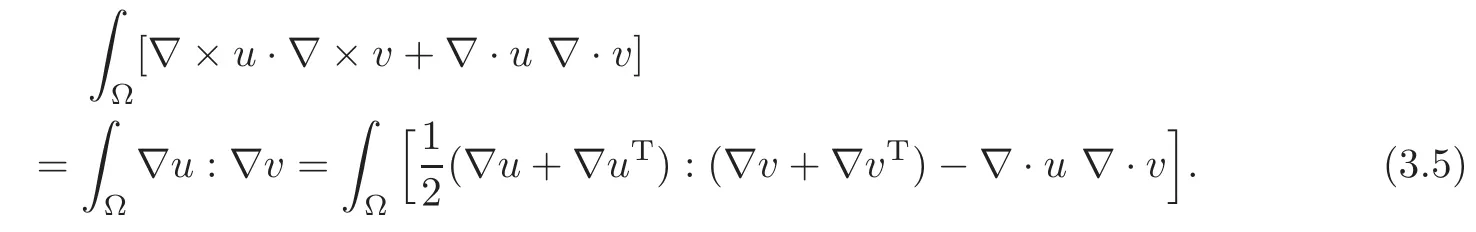
To summarise,the curl-curl formulation is the one supported by the theory while(3.3)is the one that the practioner demands,but they are equivalent in the context of the surface pressure model because u×n=0 on the∂Ω.

4 The Fluid-Structure Interaction Problem

4.1 Variational form of the model for[,p,η]

Coupling the two systems of(2.2)–(3.3)and writing the continuity of the velocities at the interface Σ,namely,lead to findingwith u × n=0,η|Γ=0 and

It must be noted that Ω and its boundary are functions of time and must be updated by the displacementas in[11].As it is unfeasible to move Γ,we assume that η|Γ=0.

An energy conservation identity is obtained as follows by letting

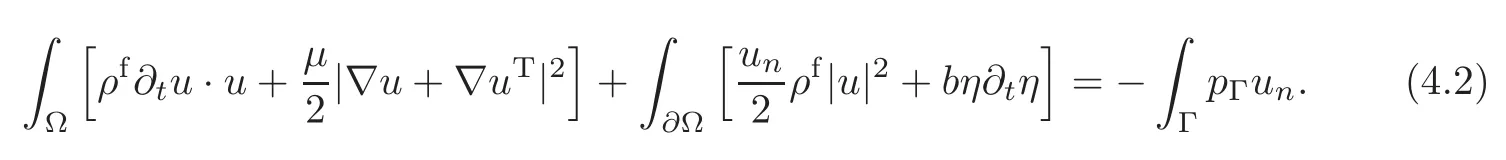
Making use of the identity

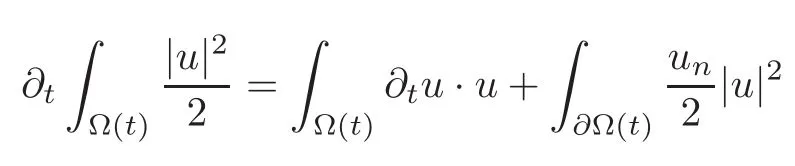
when the boundary moves with speed un,we come to

Thus kinetic energy decreases due to viscosity when Γ = ∅.

The curl-curl low Reynolds approximation of(4.1)consists in finding[u,p,η]with u×n|∂Ω=0,η|Γ=0 and

Following[14],existence and uniqueness can be shown,subject to the regularity hypotheses,because the bilinear formis strongly elliptic in the appropriate space of curl free vector fields and the bilinear formsatisfies the inf-sup condition.

5 A Hierarchy of Approximations on Fixed Domains

First note that σnn|Γ≈ −p,becauseµ is small and ∇u ≈ I∂nun≈ 0 due to u× n=0.Therefore,at the moving wall Σ,

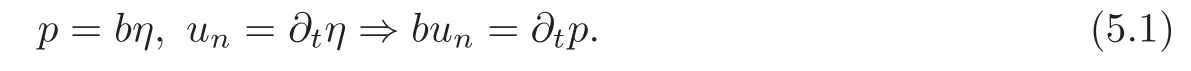
To simplify notations let us work with the reduced pressureThen with(5.1)is unchanged.

Now recall the concept of transpiration condition(see[9,28]).Instead of applying a boundary condition on a wall Σ(t)moving normally by η(x,t),we shall apply it on a fixed wall Σ with a correction factor based on the following:

If the radius of curvature of Σ is large and if u × n|∂Ω=0,then,as said earlier,

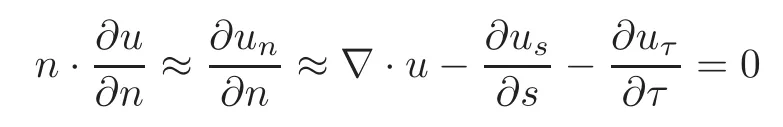
implying that the transpiration correction is of higher order.

So instead of(4.1),a simpler formulation is obtained after distcretization in time and on a fi xed domain.Together with(5.1),we must then solve(5.2)below.

5.1 A model with velocity and pressure only

Consider the following problem.

Find[um+1,pm+1]with um+1×n=0 and

We use the identity:and we remove the last term which is compensated by the moving domain in(4.1)and which ought to be absent in the fixed domain model to preserve energy(an approximation of order 2 in un|Σ),assumed small from the start.Indeed,integration by parts leads to

Then,in the case Γ = ∅,an energy estimate is obtained by lettingin(5.2),which leads to the following identity:

5.2 A model involving only the pressure

In a strong form,(5.2)is

Taking the divergence of the PDE and its scalar product with n leads to

Note that it could also be found from(5.2)by choosing

When u× ∇ × u and ν∆u ·n|Σare small,an autonomous equation for p is

where −∆Σis the Steklov-Poincaré operator

Two comments:

(1)While ν∆u ·n|Σis generally small for aortic flow,u × ∇ × u may not be;except when the flow is irrotational,which is the case only if the flow is nearly the Poiseuille pipe flow.So(5.6)is clearly only a first approximation to the problem.

(2)Resonance may occur in(5.6)atwhich is an important observation that could explain why the full problem on a moving domain is so hard and algorithms nearly unstable.

Resonance is due to the finite length of the aortic geometry used in the computation.

To estimate the resonance frequency is easy in 2D:Take a rectangle(0,L)×(−R,R)and the data in(2.3).

If p(x,y)=f(x)g(y),then −∆p=0 leads to f′′+a2f=0, −g′′+a2g=0,as g is maximum at y=0,g=cosh(ay),and thus g′(R)=asinh(aR).

Similarly,as f(0)=f(L)=0,f=sin(ax)with the necessary condition that aL=kπ,k ∈N+.So the eigenvalue problem is

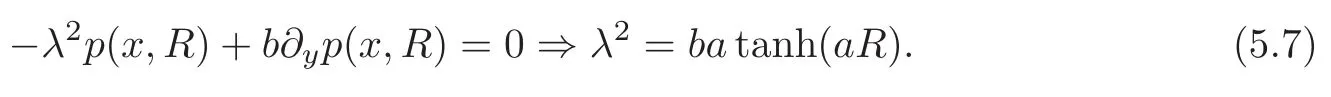
When aR is small,so the first eigenvalue is λ1=0.9cm.

6 Discretization with a Finite-Element Method

Let Thbe a triangulation with K tetrahedraunder the usual conformity hypotheses,and let

Consider the P2−P1element built from

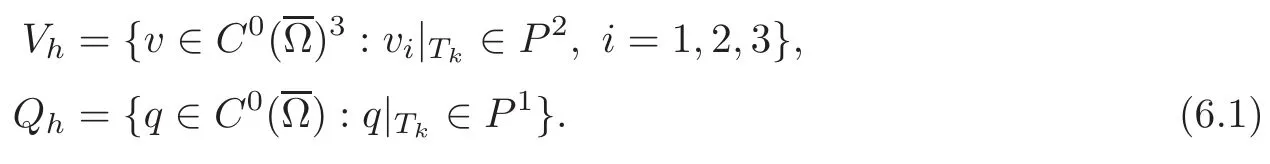
6.1 Discretization of the full problem(4.1)

A feasible discretization of(4.1)is to find[um+1,pm+1,ηm+1]∈ Vh×Qh×Qhwith um+1×n|Γ=0,ηm+1|Γ=0 such that

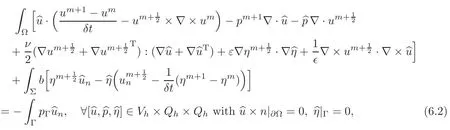
where ε is any small positive parameter.

When Ω is kept fixed,an energy conservation identity is found by choosing

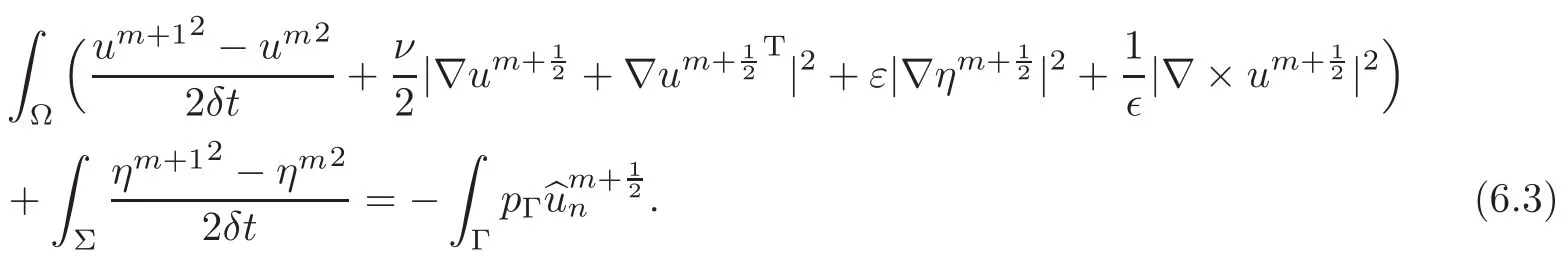
As for the Navier-Stokes equations,when δt is small enough,the problem has a unique solution because of the energy estimate and because of a general inf-sup condition is satisfied with p replaced by[p,η].

6.2 Discretization of problem(5.2)in[u,p]

A feasible discretization of(5.2)is to find um+1∈Vh,pm+1∈Qhwith um+1×n|Γ=0 and such that

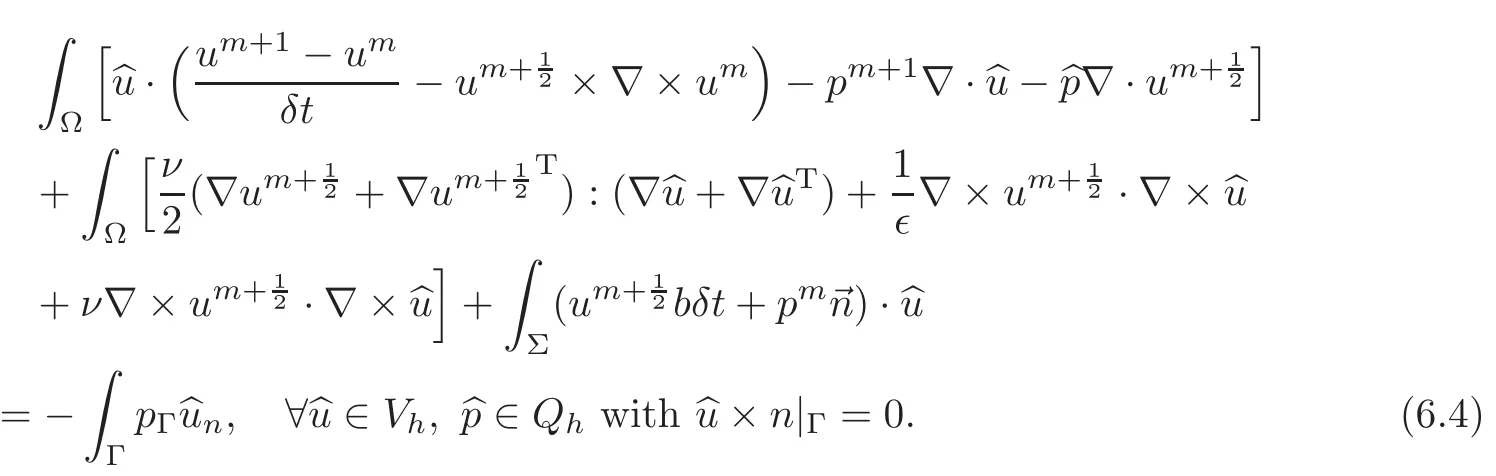
When Γ is f l at and perpendicular to an axis,um+1× n|Γ=0 amounts to some component of the velocity being zero;it is easy to implement.If not,then it must be added by penalty in the variational formulation.

The difference to a standard Stokes problem is only the added integral on Σ which reinforces the ellipticity of the bilinear form.Thanks to the inf-sup condition,the problem is well-posed.Error estimates,however,need to be rederived.

Notice that the energy equality does not imply stability,

6.3 Stability

For a high Reynolds number,some upwinding must be applied.Then it is easier to revert to u·∇u for the nonlinear term and to use the Characteristic-Galerkin method(see[30,33]for a second order version).At each time step,one seeks for um+1∈Vh,pm+1∈Qhwith um+1×n|Γ=0 and

where Xm(x)is a first-order volume preserving(because∇·um≈ 0)approximation of the solution at tmof

To be equivalent to(6.4)an integral ofshould be added to(6.6),but we know that this term ought to be neglected when we pass from a varying domain to a fixed domain.To preserve energy,we suggest to drop the term,which means that the formulation is valid approximately if and only if um|Σis small.

Indeed,assuming no quadrature error and choosinglead to

But again the last term seems hard to bound.

A similar use of the Characteristic-Galerkin method can be applied to(6.4)and there stability is not a problem,so though more expensive,(6.4)is mathematically a better formulation.

6.4 Discretization of(5.2)with operator decomposition

We can make explicit use of the boundary condition on the pressure and make a Chorin-like decomposition of(5.2).The following problems are solved in sequence:

Parallel implementations could take advantage of such decomposition.However it is not clear that an iterative solution of the full system by block decomposition(see[6,18])is not faster than this Chorin-like decomposition.Second order decomposition should also be studied in this context(see[21,31]).

6.5 Discretization of the pressure problem(5.6)

Alternatively,no such difficulty arises with the pressure equation(5.6).The following scheme,for instance,is stable with a fixed geometry:

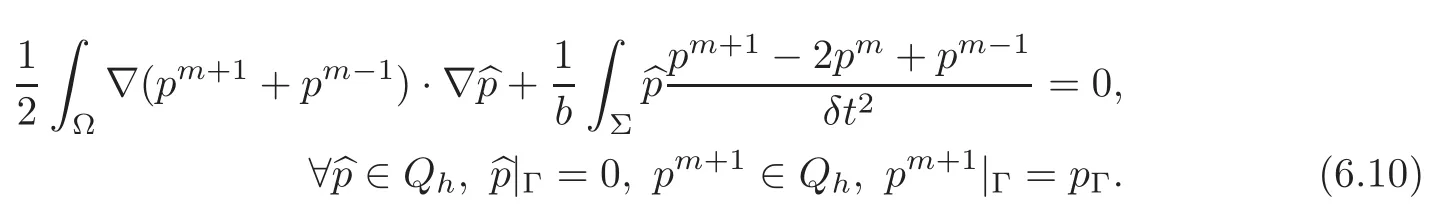
6.6 Moving the geometry for graphic visualization

The theory requires that Σ be moved at every time step along its normal of a quantity δtumTo preserve the triangulation,we follow[9],solve an additional problem

and then move every vertex qjof the triangulation qj→ qj+ κd.In theory κ =1 but for graphic enhancement,it can be adjusted.Note however that(6.11)is expensive to solve.

7 Numerical Tests

7.1 Comparison of the four methods

We begin with a comparison of(6.2),(6.6)and(6.9)–(6.10)on a simple geometry:A quarter of a torus with a pressure drop imposed from the top horizontal cross section to the right vertical one.The geometry is not updated but moved for graphic rendering.

The cross section of the torus is a circle of radius 1cm.This circle is extruded to a greater circle of radius 4cm.The pressure drop is 6cos,b=200 and ν =0.001.The time step is 0.05,voluntarily large to illustrate stability.The computation is stopped at t=0.75.

Figure 1 shows the pressure at t=0.75 by the four methods.It is seen that(6.2)and(6.6)give the same results.However while(6.9)–(6.10)agree with each other(an indication that u×∇×u is small),they only agree qualitatively with(6.2).The computing time is given in Table 1.

Table 1 Computing time for(6.2),(6.6)and(6.9)–(6.10)Method [u,v,w,p,η] [u,v,w,p] p → [u,v,w] p CPU 10.9 9.6 31.5 5.38

The linear systems are solved with the library UMFPACK which explains why(6.9)is so much more expensive.The mesh has 1395 vertices giving 6975 degrees of freedom for each linear system for[um+1,vm+1,wm+1,pm+1,ηm+1].

Figure 2 shows the values of|u×∇×u|and νnT(∇u)n when the flow is computed using the[u,v,w,p]model.It is seen that νnT(∇u)n is not small at the lower section while νnT(∇u)n is small everywhere.

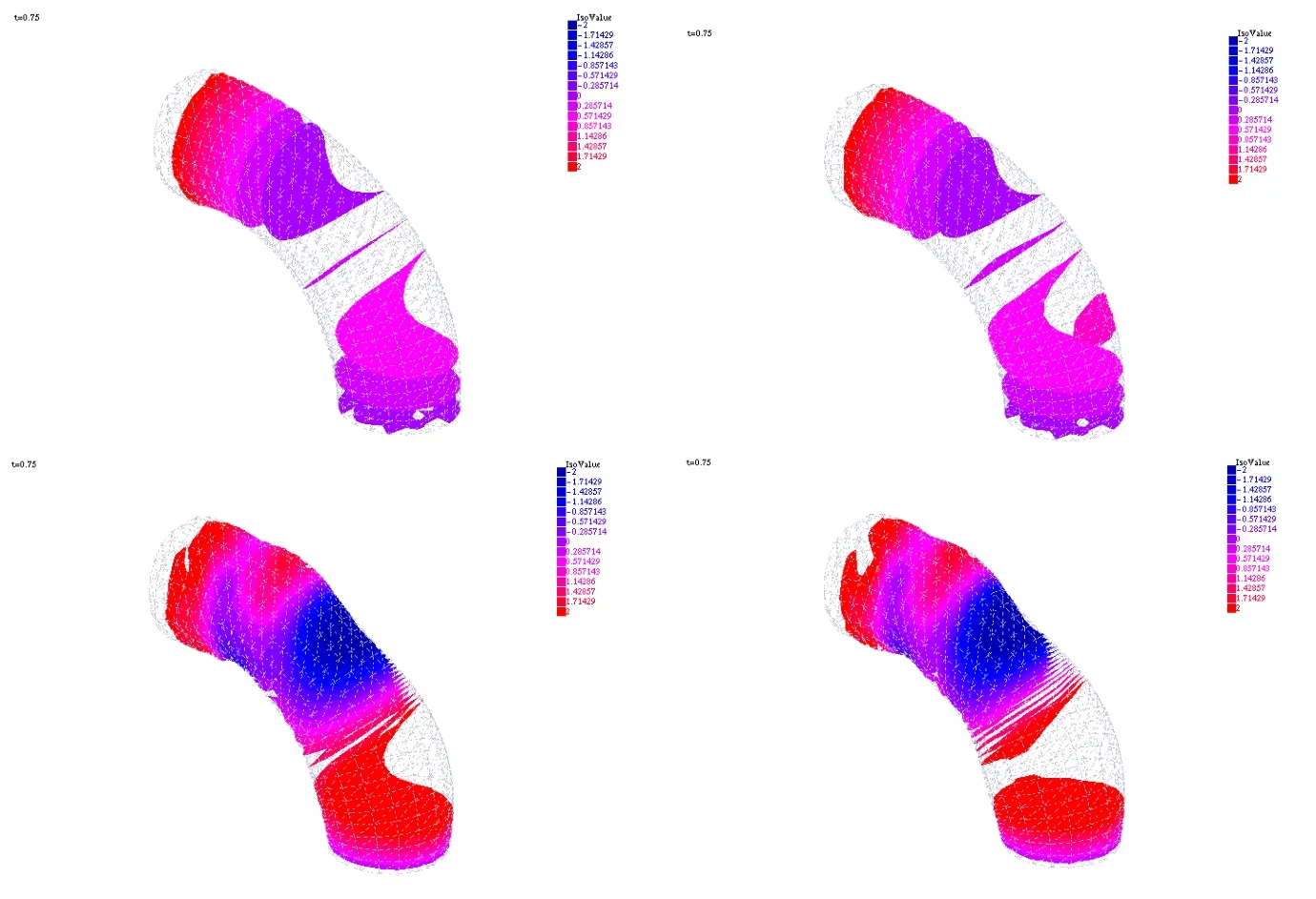
Figure 1 Top left:Computation of[u,v,w,p,η]with(6.2).Top right:Computation of[u,v,w,p]with(6.6).Bottom left:Computation of[u,v,w,p]using operator decomposition(6.9).Bottom right:Computation of the pressure only p with(6.10).

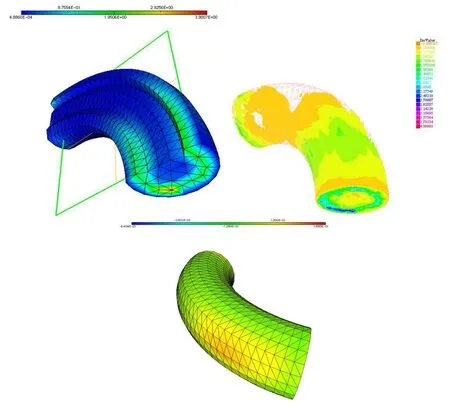
Figure 2 Top:Two views of|u×∇×u|.Bottom:νnT(∇u)n on the wall of the vessel.The lower section of the tube faces the reader.

7.2 Performance for the aorta

The geometry is a section of the aorta obtained from an MRI scan.It has 4991 vertices,giving 19964 degrees of freedom for each linear system forThe pressure drop from the inflow section on the right to the outflow section on the left is pΓR=6cos2(πt)and the results are shown at t=0.8.On the smaller cross sections,a pressure drop equal tois imposed.(6.6)is used with δt=0.05, ν =0.001 and b=200.The computation took 342′′on a macbook pro 15′′,2012,2.3MHz core i7(see Figure 3).

Figure 3 Computation of[,p]with(6.6)for an aorta.Left:Pressure at t=0.8.The compliant walls are updated for graphic visualization of the compliant wall deformation.On the left,the vertical velocity u3at t=0.8 without graphic enhancement shows also the geometry used for the computation.

7.3 Performance on a documented stenosed carotid bifurcation flow

In this section we reproduce the computational results of pulsatile flow in human carotid bifurcation models(see[19–20]).The studies referred to assumed rigid wall arteries.We further extend those results to the full fluid-structure interaction problem with compliant walls.

We have modeled a 10 cm long representative healthy carotid artery bifurcation model,along with 30%and 64%concentrically stenosed models.The common carotid artery has a diameter of 9mm,while the internal and external carotid arteries have a diameter of 6.8mm and 5.6mm,respectively.All artificial boundaries are perpendicular to x-axis.Finite-element meshes(coarse discretization h=0.2mm,1885 vertices)are shown in Figure 4.Fine discretizations are built with h=0.04mm resulting roughly in 2·105vertices and one million tetrahedral elements.

First,in order to compare our results with those cited above,we consider Σ to be a rigid wall.We also replaced the inlet boundary conditionby the velocity pro fi le

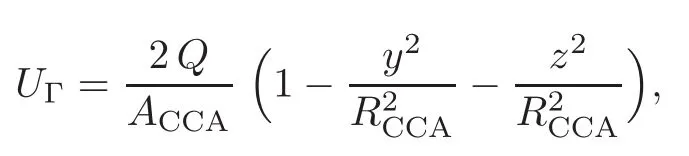
where Q is the flow rate depicted in Figure 4(right).Spline interpolation is used to fit the pointwise data;traction-free boundary conditions are imposed at the outlet boundaries.

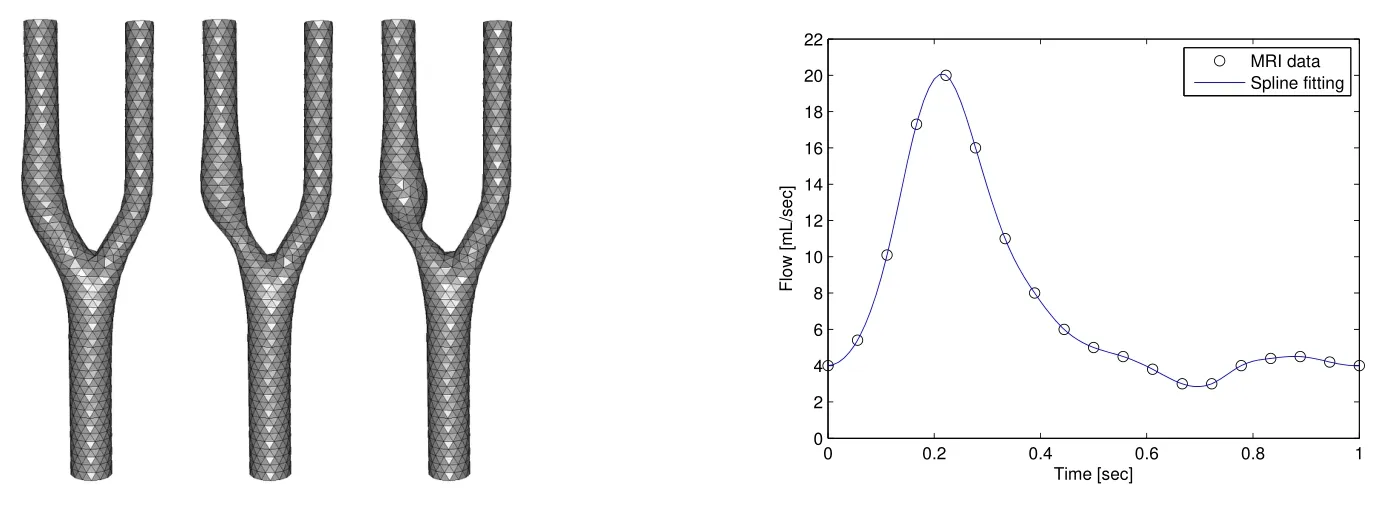
Figure 4 Carotid bifurcation:Healthy(left),30%(middle),64%(right)stenosed models(coarse discretization).Flow rate waveform at the common carotid artery inlet.

The initial velocity-pressure field at t=0 is set to be a solution of the Oseen equation.The time step is 0.01.Five cardiac cycles are sufficient to eliminate transient effects caused by initial conditions,and to obtain cyclically repeated flow patterns.For the considered geometries,the inlet flow together with ν =3.5 ·10−3Pa·sec and ρ=1060kg ·m−3result in a Reynolds number of a few hundred;Re at the inflow surface is 357,Re at the 64%stenosed area is 1280.Excellent agreement with the published results was observed in booth magnitude and location of flow patterns.

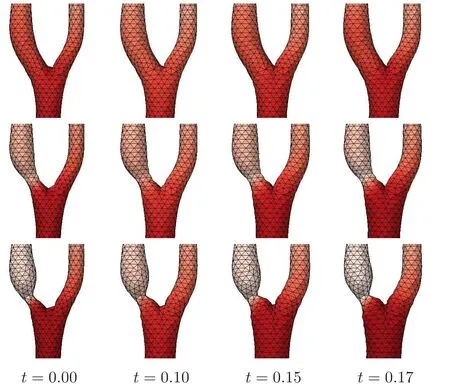
Figure 5 Carotid bifurcation.Arterial displacement during the pre-systolic period;top to bottom:Normal,30%,64%stenosis.Dark red color marks regions of higher pressure.

Now we use(6.6)with b=200 and δt=0.01.The geometry is fixed for the numerical simulations but updated for graphic rendering,κ=100.We observe that for all three models the maximum positive displacement,i.e.expansion(>0),is at t=0.17,while the maximum negative displacement,i.e.contraction,is at t=0.64.Figure 5 shows the updated shape of the bifurcation region at four selected phases of the cardiac cycle:t=0,t=0.1,t=0.15 and t=0.17.The red color marks regions with higher pressure.We observe that the healthy artery undergoes a uniform expansion/contraction in the entire domain.For the stenosed arteries,displacements become much larger in the portion of the internal carotid artery below the bifurcation;we identify tiny displacements downstream from the stenosis.More importantly,a steep change in pressure near the stenosis region observed for both 30%and 64%stenosis models will produce an increasing shear stress that could be a reason for arterial rupture.

This paper demonstrates that(6.6)allows physiologically realistic blood flow analysis.A hierarchy of approximations helps reducing the overall computational ef f ort of updating the triangulation at every time step.On the other hand,the method allows us to inspect arterial compliance at arbitrary phases of the cardiac cycle.More importantly,moving the geometry for graphic visualization can be done as a post-processing task,or in parallel.

[1]Begue,C.,Conca,C.,Murat,F.and Pironneau O.,Les equations de Stokes et de Navier-Stokes avec conditions aux limites sur la pression,Nonlinear Partial Differential Equations and Their Applications,H.Brezis,J.Lions(eds.),College de France,Vol.IX,Pitman,RNM Longman,Boston,1988,179–264.

[2]Boffi,D.and Gastaldi,L.,A finite element approach for the immersed boundary method,Comput.Struct.,81,2003,491–501.

[3]Costabel,M.and Dauge,M.,Maxwell and Lamé eigenvalues on polyhedral domains,Université de Rennes I,2002,preprint.

[4]Costabel,M.and Dauge,M.,Singularities of electromagnetic fields in polyhedral domains,Université de Rennes,1,1997,preprint 97-19.http://www.maths.univ-rennes1.fr/∼dauge/

[5]Cottet,G.H.,Maitre,E.and Milcent,T.,Eulerian formulation and level set models for incompressible fluid-structure interaction,ESAIM:M2AN,42,2008,471–492.

[6]Crosetto,P.,Deparis,S.,Fourestey,G.and Quarteroni,A.,Parallel algorithms for fluid-structure interaction problems in haemodynamics,SIAM J.Sci.Comput.,33(4),2011,1598–1622.

[7]Decoene,A.and Maury,B.,Moving meshes with freefem++,J.Numer.Math.,20(3–4),2013,195–214.

[8]De Hart,J.,Peters,G.,Schreurs,P.and Baaijens,F.,A three-dimensional computational analysis of fluid-structure interaction in the aortic value,J.Biomechanics,36,2003,103–112.

[9]Deparis,S.,Fernandez,M.A.and Formaggia,L.,Acceleration of a fixed point algorithm for fluid-structure interaction using transpiration conditions,ESAIM:M2AN,37(4),2003,601–616.

[10]Hu,F.Q.,Li,X.D.and Lin,D.K.,Absorbing boundary conditions for nonlinear Euler and Navier-Stokes equations based on the perfectly matched layer technique,J.Comp.Physics,227,2008,4398–4424.

[11]Fernandez,M.,Incremental displacement-correction schemes for incompressible fluid-structure interaction,Numer.Math.,123,2013,21–65.

[12]Formaggia,L.,Gerbeau,J.F.,Nobile,F.and Quarteroni,A.,On the coupling of 3D and 1D Navier-Stokes equations for flow problems in compliant vessels,Comput.Methods Appl.Mech.Engrg.,191,2001,561–582.

[13]Formaggia,L.,Quarteroni,A.and Veneziani,A.,Cardiovasuclar Mathematics,Springer MS&A Series,Springer-Verlag,New York,2009.

[14]Girault,V.and Glowinski,R.,Error analysis of a fictitious domain method applied to a Dirichlet problem,Japan Journal of Ind.and Applied Math.,12(3),1995,487–514.

[15]Girault,V.and Raviart,P.A.,Finite Element Method for Navier-Stokes Equations,SCM 5,Springer-Verlag,Berlin,Heidelberg,NewYork,1986.

[16]Gonzalez,O.and Simo,J.C.,On the stability of symplectic and energy-momentum algorithms for nonlinear Hamiltonian systems with symmetry,Comput.Methods Appl.Mech.Engrg.,134,1996,197–222.

[17]Gonzalez,O.,Exact energy and momentum conserving algorithms for general models in nonlinear elasticity,Comput.Methods Appl.Mech.Engrg.,190,2000,1763–1783.

[18]Gostaf,K.,Pironneau O.and Roux,F.X.,Finite element analysis of multi-component assemblies:CAD-based domain decomposition,DDM 14 Proc.,to appear.

[19]Marshall,I.,Computational simulations and experimental studies of 3d phase-contrast imaging of fluid flow in carotid bifurcation geometries,J.Magnetic Resonance Imaging,31,2010,928–934.

[20]Steinman,D.A.,Poepping,T.L.,Tambasco,M.,et al.,Flow patterns at the stenosed carotid bifurcation:Ef f ect of concentric versus eccentric stenosis,Annal.Biomedical Engineering,28,2000,415–423.

[21]Guermond,J.L.,Minev,P.and Shen,J.,An overview of projection methods for incompressible flows,Comput.Methods Appl.Mech.Engrg.,195(44–47),2006,6011–6045.

[22]Heil,M.,Hazel,A.and Boyle,J.,Solvers for large-displacement fluid-structure interaction problems:Segregated versus monolithic approaches,Comput.Mech.,43,2008,91–101.

[23]Le Tallec,P.,Fluid structure interaction with large structural displacements,Comput.Methods Appl.Mech.Engrg.,190,2001,3039–3067.

[24]Nobile,F.and Vergara,C.,An effective fluid-structure interaction formulation for vascular dynamics by generalized robin conditions,SIAM J.Sci.Comp.,30(2),2008,731–763.

[25]Pares,C.,Un traitement faible par élément finis de la condition de glissement sur une paroi pour leséquations de Navier-Stokes,C.R.Acad.Sci.Paris Sér.I Math.,307,101–106,1988.

[26]Peskin,C.,The immersed boundary method,Acta Numerica,11,2002,479–517.

[27]Peskin,C.and McQueen,D.,A three dimensional computational method for blood flow in the hearth-I,Immersed elastic fibers in a viscous incompressible fluid,J.Comput.Phys.,81,1989,372–405.

[28]Pironneau,O.,Finite Element Methods for Fluids,Wiley,New York,1989.

[29]Pironneau,O.,Conditions aux limites sur la pression pour leséquations de Stokes et de Navier-Stokes,C.R.Acad.Sci.Paris Sér.I Math.,303(9),1986,403–406.

[30]Pironneau,O.and Tabata,M.,Stability and convergence of a Galerkin-characteristics finite element scheme of lumped mass type,Int.J.Numer.Meth.Fluids,64,2010,1240–1253.

[31]Rannacher,R.,Incompressible Viscous Flow,Encyclopedia Mecanicae,E.Stein(ed.),Wiley,New York,2004.

[32]Rappaz,J.and Flotron,S.,Numerical conservation schemes for convection-diffusion equations,to appear.

[33]Si,Z.Y.,Second order modified method of characteristics mixed defect-correction finite element method for time dependent Navier-Stokes problems,Numer.Algor.,59,2012,271–300.

[34]Tambaca,J.,Canic,S.,Kosor,M.,et al.,Mechanical Behavior of Fully Expanded Commercially Available Endovascular Coronary Stents,Tex Heart Inst.J.,38(5),491–501,2011.

[35]Thiriet,M.,Biomathematical and biomechanical modeling of the circulatory and ventilatory systems,Control of Cell Fate in the Circulatory and Ventilatory Systems,Vol.2,Math and Biological Modeling,Springer-Verlag,New York,2011.

[36]Usabiaga,F.,Bell,J.,Buscalioni,R.,et al.,Staggered schemes for fluctuating hydrodynamics,Multiscale Model Sim.,10,2012,1369–1408.

[37]Vignon-Clementel,I.,Figueroa,A.,Jansen,K.and Taylor,C.A.,Outflow boundary conditions for threedimensional finite element modeling of blood flow and pressure in arteries,Comput.Methods Appl.Mech.Engrg.,195,2006,3776–3796.