Two-Level Additive Schwarz Methods Using Rough Polyharmonic Splines-Based Coarse Spaces∗

Rui DU Lei ZHANG

(In Honor of the Scientific Contributions of Professor Luc Tartar)

1 Introduction

Problems with many scales are ubiquitous in nature.Among all the multi-scale problems,the following divergence-form scalar elliptic equation(1.1)with highly heterogeneous coefficients α(x)∈ L∞(Ω)is perhaps the most intensively studied one,with a wide range of applications in reservoir modeling,composite materials,etc.Our main objective in this paper is to develop and test a class of overlapping domain decomposition methods using the so-called rough polyharmonic splines(RPS for short)based multiscale coarse grid solvers,which is a multiscale basis with the optimal convergence rate and the optimal localization property(see[23]).

The contrast of α(x)is expressed as the ratio between high and low conductivity values and defined by

which brings a small scale into the problem.This type of problems commonly arises in several fields that include subsurface flows and oil reservoir modeling as the representative examples.

The domain decomposition method is a powerful tool to construct efficient parallel solvers for large-scale linear systems arising from the fine scale discretization of partial differential equations(see[26,28]).To construct preconditioners for the fine-scale system,domain decomposition algorithms include small local problems in the subregions and a coarse problem.Note that without a coarse space component,the algorithms cannot be scalable,i.e.,they have a rate of convergence independent of the number of subregions.

The number of iterations required by domain decomposition based methods is determined by the condition number of the preconditioned system.Therefore,the design of preconditioners must address the effects of the following two issues on the condition number,the size of the problem,and the contrast in the media properties.Commonly used domain decomposition methods(see[19,26,28])can make the condition number of the preconditioned system independent of the system size for certain problems including the scalar elliptic equation(1.1).

The design of robust preconditioners with respect to the contrast turns out to be a more challenging problem.When the variation of coefficients is mild inside the coarse-grid blocks,classical domain decomposition preconditioners with a linear coarse space result in a system with the condition number independent of the contrast(see,e.g.,[19,28]).If the variation of coefficients is large inside coarse grid blocks,the classical method fails to be robust.In this case,a judicious choice of the coarse space is the key to constructing the robust domain decomposition preconditioner which has a condition number independent of the coefficient contrast.

In recent works[1,11,14],robust preconditioners with respect to the contrast were constructed with the help of coarse space adaptive to small scale features.The connection between multiscale finite elements and robust preconditioners was first explored in[1].In[14–15],robust preconditioners were constructed for a variety of binary(i.e.,two-scale)media model problems using multiscale finite element based coarse space.In a series of works[9–12],the coarse space was further enriched by local spectral basis functions to be suitable for high contrast problems.It is now well understood that the construction of coarse space is closely associated with the development of the multiscale finite-element methods,or in the general sense,numerical homogenization methods.

To this end,we would like to give a very short introduction about numerical homogenization.The field of numerical homogenization concerns the numerical approximation of the solution space of(1.1)with a finite-dimensional space.This problem is motivated by the fact that standard methods,such as the finite-element method with piecewise linear elements(see[4]),can perform arbitrarily badly for PDEs with rough coefficients such as(1.1).Although some numerical homogenization methods are developed from classical homogenization concepts such as periodic homogenization and scale separation(see[5]),as well as localized cell problems(see[24]),one of the main objectives of numerical homogenization is to achieve a numerical approximation of the solution space of(1.1)with arbitrary rough coefficients(i.e.,in particular,without the assumptions found in classical homogenization,such as scale separation and ergodicity at fine scales).In this direction,oscillating test functions,G or H-convergence and compensated compactness(see[13,20,27])have always been a great source of inspiration.Professor Luc Tartar has made profound contribution to the development of the above theories.The multiscale finite-element method(MsFEM for short)(see[8,16–17])can be seen as a numerical generalization of the idea of oscillating test functions found in H-convergence(see[20])and was justified for problems with scale separation.For problems with nonseparable scales,the authors and collaborators proposed the method of harmonic coordinates for scalar elliptic equations in 2D(see[21]).In[6],the transfer property of the flux-norm was introduced to identify the global basis,and then in[22]the computation of the basis was localized to sub-domains of sizeIn[22],we also concluded the strong compactness of the solution space,which guarantees the existence of an accurate finite-dimensional approximation space as long as the right-hand side is not too singular.Then the name of the game becomes how to achieve such a finite-dimensional space with the least cost,namely,a space with the best localized basis.

In[23],we introduced an approximation space generated by an interpolation basis over scattered points with resolution H which minimizes the L2norm of the source terms;its(pre-)computation involves minimizing O(Hd)quadratic(cell)problems on(super-)localized sub-domains of sizeThe resulting interpolation basis functions are biharmonic for d≤3,and polyharmonic for d≥4 and can be seen as a generalization of polyharmonic splines to differential operators with arbitrary rough coefficients.Therefore,the basis is called rough polyharmonic splines(RPS for short).The accuracy of the method O(H)in the energy norm is optimal and independent of aspect ratios of the mesh formed by the scattered points.For development in this direction,please also see[3,18].

In this paper,we use RPS to construct the coarse space of the domain decomposition method,and evaluate the performance of RPS-based preconditioners with some typical domain decomposition preconditioners(linear and MsFEM-based).We apply our method to some benchmark problems and obtain promising numerical results.Theoretical justification of the method is in progress.

2 Mathematical Formulations

In this section,we present the continuous and discrete formulations of the problems that will be considered for preconditioning.

Consider the variational formulation of(1.1)as follows:Findsuch that

where

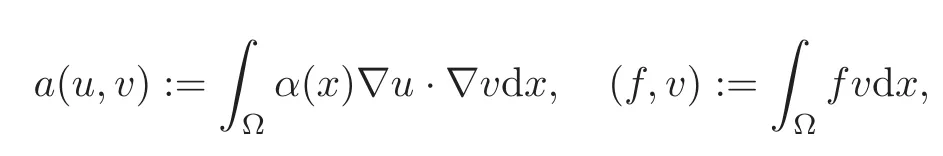
where Ω ⊂ R2is a bounded polygonal domain,and f(x)∈ L2(Ω).The coefficients α(x)≥ α0>0,and α(x)∈ L∞(Ω)are allowed to be highly variable in an unstructured way and have a high contrast in Ω.Without loss of generality,we assume that α0≥ 1 which can always be achieved by scaling the problem with

Let the domainand Ωibe disjoint-shape regular polygonal subdomains of diameters Hi.Denote the subdomain boundaries by ∂Ωi.For each Ωi,we introduce a quasi-uniform triangulation Tiby triangles with the mesh size hi.The resulting triangulation Thon Ω is assumed to be conforming,i.e.,the subdomain meshes match across∂Ωi.

Without loss of generality,we assume that the coefficient α(x)restricted to any fine triangle τ∈ This a constant,denoted by ατ.The analysis will depend on the coefficient on a boundary layer near subdomain boundaries.For each subdomain Ωi,we define the boundary layer Ωhias the union of fine triangles in Ωithat touch the boundaries ∂Ωi.Then we set

Denote by Vh(Ω)the standard finite-element space of continuous functions on the domainΩ,which are piecewise linear on the fine mesh Thand vanishing on ∂Ω.The discrete problem of(2.1)is of the following form:Find uh∈ Vh(Ω)such that

This weak form results in a linear system as

where the global stiffness matrix A is large,sparse,and symmetric positive definite,and f is the load vector corresponding to the right-hand side of(2.3).

3 Additive Schwarz Methods with RPS-Based Coarse Spaces

The two-level additive Schwarz methods use the solutions of local problems and a coarse problem to construct preconditioners for the fine scale system(2.4).In this section,we introduce an additive Schwarz method with the RPS approximation space as a new coarse space.The construction of RPS generalizes the well-known concepts of polyharmonic splines(see[2,7,25]).Unlike standard polyharmonic splines,RPS incorporates information about the coefficients α(x).In[23],the properties of RPS,necessary for construction of an optimal localized computational basis,were established and rigorously justified.

We denote bythe overlapping partition from the original nonoverlapping partitionby extending each subregion Ωiinto

where the dist is some distance function.Here we consider the case of minimal overlap with δi=hi,that is, Ωiis extended toby adding one layer of fine triangles in Tithat touch the outside of∂Ωiby edges and/or vertices.The space Vh(Ω)can be decomposed as follows:

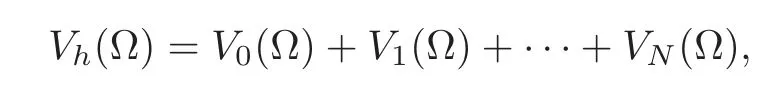
where

The local matrix is defined bywhereis the extension by zero operator.

The coarse space V0(Ω)will be defined in a special way with the coarse basis functionswhere Ncis equal to the number of coarse nodes excluding those on the global boundary ∂Ω.We associate a specific function Φkwith each coarse node xk,i.e.,a rough polyharmonic spline centered at xk.The definition of RPS is provided below(see also[23]).

我国网络经济发展迅猛，但现行的税法并不完善，按照现行税法无法完全对网络购物行为进行征税，这也是大量网购不开发票也不缴税，网购价格低的重要原因。从税收公平视角来说，税收不应该由于商业模式的不同而有所差异。国家应加强网络经济税收征管，适应电子商务发展要求，利用信息化手段创新税收征管方式，减少税收流失，创造有序竞争的市场环境和公平公正的税收环境。

Let V be the set of functionssuch that div(α∇u) ∈ L2(Ω).Let k.kVbe the norm on V defined by

For each coarse node xkwe define

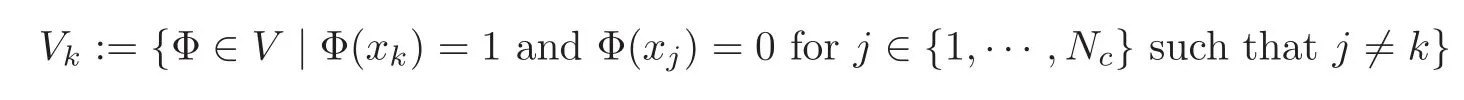
and consider the following optimization problem over Vk:

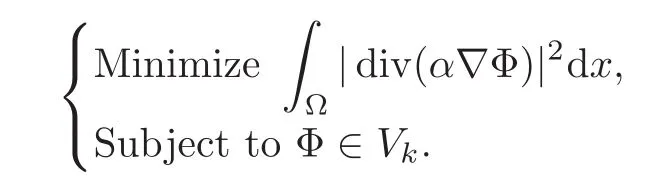
It was shown in[23]that the minimizer of the above problem exists and is unique,which can be finally identified as the coarse basis function Φk.

Then we can define

and the coarse matrixwhereis the fine nodal point.The corresponding two-level additive Schwarz preconditioner is of the form

Theorem 3.1The condition numbers of the preconditioned stiffness matrices using the proposed two-level additive Schwarz preconditioners satisfy

Remark 3.1For the proof of Theorem 3.1,we follow the general abstract theory for the additive Schwarz methods developed in[26,28].Using the same abstract arguments,the proof follows by checking three assumptions.We start with Assumption II(strengthened Cauchy-Schwarz inequalities)and Assumption III(local stability)which are quite easy to verify.In our case,this is straightforward to prove that ρ(E)=1 and ω =1 in these two assumptions,respectively.Finally,we only need to check the constant in Assumption I(stable decomposition).

The sharpness of the dependence on the contrast and the mesh ratio in(3.5)will be verified numerically in the next section,while the rigorous proof remains the work in progress.

4 Numerical Results

Let the domain Ω be a unit square(0,1)2.We firstly triangulate Ω into N × N equal coarse squares,then decompose each coarse square into M×M equal fine squares and divide each fine square into two sub-triangles along its diagonal with a positive slope.The distribution of coefficients in each example is presented by figures,where α(x)=b α in the red shaded region,and α(x)=1 else where.We use the additive Schwarz method with RPS-based coarse spaces(see Section 3),and iterate with the preconditioned conjugate gradient(PCG for short)method.The iteration in each test stops whenever the l2norm of the residual is reduced by a factor of 10−6.

4.1 Dependence on the contrast

We implement the two-level additive Schwarz methods with RPS-based coarse spaces for Examples 4.1–4.2(see Figure 1)to investigate how the condition numbers of preconditioned systems depend on the contrast in the coefficients.Here we take N=8 and M=8,i.e.,and

Figure 1 Left:Example 4.1.Right:Example 4.2.

In Example 4.1,the high-conductivity subregions are completely in the interior of subdomains,while the high-conductivity subregions are only in the boundary layers in Example 4.2.The results in Table 1 indicate that the condition numbers are independent of the contrast in the interior of subdomains,while they may(linearly)depend on the contrast in the boundary layers.

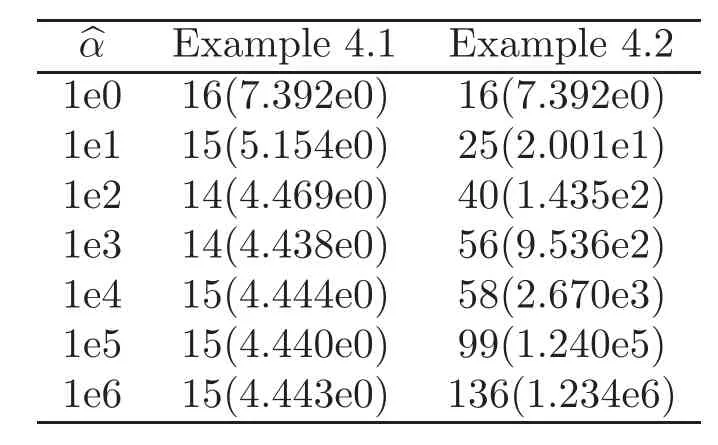
Table 1 Examples 4.1–4.2.Iteration numbers(condition numbers)for different values of contrast,coarse dof 49.

4.2 Dependence on the mesh ratio

We test the proposed method with Example 4.1,where the distribution of coefficients is kept as shown in Figure 1 withWe change M=8,16,32,i.e.,The log-log plot of the condition numbers with respect to the mesh ratiois reported in Figure 2.The slope of the least square line in Figure 2 is approximated by 1.01,which indicates the linear dependence of the condition number on the mesh ratio.

Figure 2 The log-log plot of the condition number vs.for Example 4.1.

4.3 Comparisons

We test domain decomposition preconditioners based on the following three coarse spaces:The classical linear coarse space(linear for short),the MsFEM-based coarse space(MsFEM for short),and the global RPS-based coarse space(RPS for short).We consider three different distributions of the coefficients(see Examples 4.3–4.5 in Figure 3,and test different values of the contrast in each example).In all the three examples,we choose N=8 and M=10,i.e.,

Figure 3 Top Left:Example 4.3.Top Right:Example 4.4.Bottom:Example 4.5.

It follows from the numerical results in Tables 2–4 that for unstructured permeabilities with high contrast,domain decomposition preconditioners constructed by coarse spaces with small scale features(MsFEM and RPS)have a better performance than the classical linear coarse spaces.In particular,RPS outperforms MsFEM by 3–4 orders of magnitude in the condition number and has a much less iteration counts for the high contrast case.This difference is not so profound for the simpler case,Example 4.3,but for the more complicated permeability fields in Examples 4.4–4.5,the performance gain with RPS is also more significant.We believe it is due to the fact that RPS is a basis with the(quasi-)optimal convergence rate and the(quasi-)optimal localization property as an approximation space of the original elliptic problem(1.1).

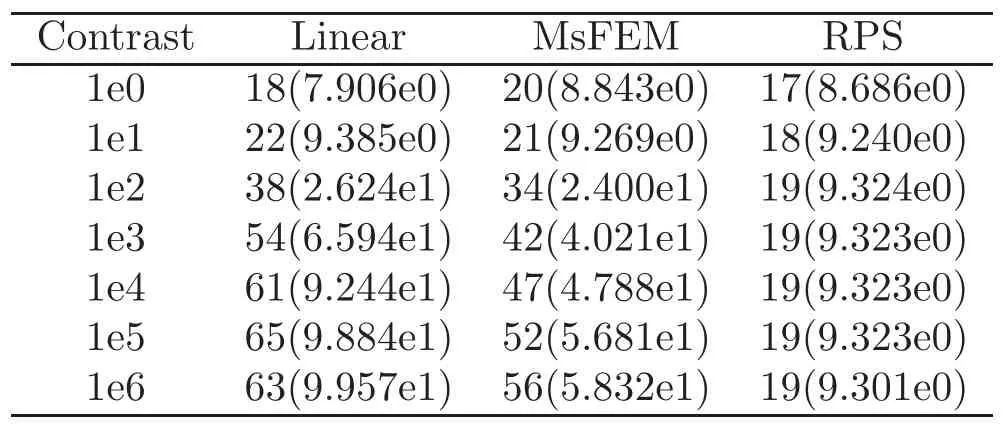
Table 2 Example 4.3.Iteration numbers(condition numbers)of different methods,coarse dof 49.

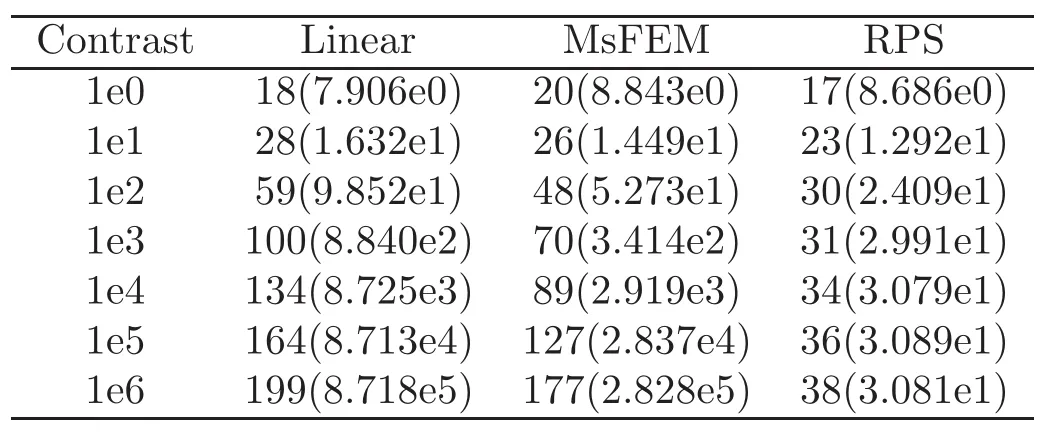
Table 3 Example 4.4.Iteration numbers(condition numbers)of different methods,coarse dof 49.

Table 4 Example 4.5.Iteration numbers(condition numbers)of different methods,coarse dof 49.

5 Conclusion

In this paper,we formulate a domain decomposition method which uses rough polyharmonic splines(RPS for short)to construct its coarse space.As RPS has quasi-optimal properties as an approximation space of the original elliptic equation(1.1),we expect that the performance of the domain decomposition preconditioner will be greatly improved,especially for problems with highly variable coefficients.This is verified numerically through several examples.The theoretical analysis is on progress,which lies in checking the assumption of stable decomposition.A promising future work is to investigate the performance of localized RPS coarse spaces.

AcknowledgementThe authors are very glad to contribute this proceeding in honor of Luc Tartar,who has contributed so much to PDE theory,and in particular,his work on homogenization has been a great source of inspiration for our studies.

[1]Aarnes,J.and Hou,T.Y.,Multiscale domain decomposition methods for elliptic problems with high aspect ratios,Acta Mathematicae Applicatae Sinica,18(1),2002,63–76.

[2]Atteia,M.,Fonctions “spline” et noyaux reproduisants d’Aronszajn-Bergman,Rev.Fran¸caise Informat,Recherche Opérationnelle,4(R-3),1970,31–43.

[3]Babuška,I.and Lipton,R.,Optimal local approximation spaces for generalized finite element methods with application to multiscale problems,Multiscale Model.Simul.,9,2011,373–406.

[4]Babuška,I.and Osborn,J.E.,Can a finite element method perform arbitrarily badly?Math.Comp.,69(230),2000,443–462.

[5]Bensoussan,A.,Lions,J.L.and Papanicolaou,G.,Asymptotic Analysis for Periodic Structure,North Holland,Amsterdam,1978.

[6]Berlyand,L.and Owhadi,H.,Flux norm approach to finite dimensional homogenization approximations with non-separated scales and high contrast,Archives for Rational Mechanics and Analysis,198(2),2010,677–721.

[7]Duchon,J.,Interpolation des fonctions de deux variables suivant le principe de la f l exion des plaques minces,Rev.Francaise Automat.Informat.Recherche Operationnelle Ser.RAIRO Analyse Numerique,10(R-3),1976,5–12.

[8]Efendiev,Y.and Hou,T.,Multiscale finite element methods for porous media flows and their applications,Appl.Numer.Math.,57(5–7),2007,577–596.

[9]Efendiev,Y.and Galvis,J.,A domain decomposition preconditioner for multiscale high-contrast problems,Domain Decomposition Methods in Science and Engineering XIX,Springer-Verlag,New York,2011,189–196.

[10]Efendiev,Y.,Galvis,J.,Lazarov,R.and Willems,J.,Robust domain decomposition preconditioners for abstract symmetric positive definite bilinear forms,ESAIM:Mathematical Modelling and Numerical Analysis,46(5),2012,1175–1199.

[11]Galvis,J.and Efendiev,Y.,Domain decomposition preconditioners for multiscale flows in high-contrast media,Multiscale Model.Simul.,8(4),2010,1461–1483.

[12]Galvis,J.and Efendiev,Y.,Domain decomposition preconditioners for multiscale flows in high contrast media:reduced dimension coarse spaces,Multiscale Modeling Simulation,8(5),2010,1621–1644.

[13]De Giorgi E.,Sulla convergenza di alcune successioni di integrali del tipo dell’aera,Rendi Conti di Mat.,8,1975,277–294.

[14]Graham,I.G.,Lechner,P.O.and Scheichl,R.,Domain decomposition for multiscale PDEs,Numerische Mathematik,106(4),2007,589–626.

[15]Graham,I.G.and Scheichl,R.,Robust domain decomposition algorithms for multiscale PDEs,Numerical Methods for Partial Differential Equations,23(4),2007,859–878.

[16]Hou,T.Y.,Wu,X.H.and Cai,Z.,Convergence of a multiscale finite element method for elliptic problems with rapidly oscillating coefficients,Math.Comp.,68(227),1999,913–943.

[17]Hou,T.Y.and Wu,X.H.,A multiscale finite element method for elliptic problems in composite materials and porous media,J.Comput.Phys.,134(1),1997,169–189.

[18]Malqvist,A.and Peterseim,D.,Localization of elliptic multiscale problems,Math.Comp.,83,2014,2583–2603.

[19]Mathew,T.P.A.,Domain Decomposition Methods for the Numerical Solution of Partial Differential Equations,Lect.Notes Comput.Sci.Eng.,Springer-Verlag,Berlin,2008.

[20]Murat,F.and Tartar,L.,H-convergence,Séminaire d’Analyse Fonctionnelle et Numérique de l’Université,1978,34 pages,English translation:Topics in the Mathematical Modelling of Composite Materials,L.Cherkarv and R.V.Kohn(eds.),Progress in Nonlinear Differential Equations and Their Applications,Vol.31,Birkhauser,Boston,1998,21–43.

[21]Owhadi,H.and Zhang,L.,Metric-based upscaling,Comm.Pure Appl.Math.,60(5),2007,675–723.

[22]Owhadi,H.and Zhang,L.,Localized bases for finite dimensional homogenization approximations with non-separated scales and high-contrast,SIAM Multiscale Modeling Simulation,9,2011,1373–1398.

[23]Owhadi,H.,Zhang,L.and Berlyand,L.,Polyharmonic homogenization,rough polyharmonic splines and sparse super-localization,ESAIM:Mathematical Modelling and Numerical Analysis,48(2),2014,517–552.

[24]Papanicolaou,G.C.and Varadhan,S.R.S.,Boundary value problems with rapidly oscillating random coefficients,Random Fields,Vol.I–II,1979;Colloq.Math.Soc.János Bolyai,27,North-Holland,Amsterdam,1981,835–873.

[25]Rabut,C.,Elementary m-harmonic cardinal B-splines,Numer.Algorithms,2(1),1992,39–61.

[26]Smith,B.F.,Petter Bjørstad and William Gropp,Domain Decomposition:Parallel Multilevel Methods for Elliptic Partial Differential Equations,Cambridge University Press,Cambridge,1996.

[27]Spagnolo,S.,Sulla convergenza di soluzioni di equazioni paraboliche ed ellittiche,Ann.Scuola Norm.Sup.Pisa,22(3),1968,571–597;errata,ibid.,22(3),1968,673.

[28]Toselli,A.and Widlund,O.,Domain Decomopsition Methods-Algorithms and Theory,Springer-Verlag,Berlin,2005.