Weak Continuity and Compactness for Nonlinear Partial Differential Equations∗
Gui-Qiang G.CHEN
(In Honor of the Scientific Contributions of Professor Luc Tartar)
1 Introduction
Nonlinear partial differential equations(PDEs)can be written in the following general form:
工作效能尚需提高。纪检组监督4家单位,重大事项较多,有时监督单位临时召开紧急会议,纪检组沟通准备不足,不能充分发表意见。有时监督单位同一天会议,纪检组人员不够,协调兼顾不到,不能很好地履行监督职责。

where N[·]is a nonlinear mapping,and U is an unknown function that is called a solution if U solves(1.1).
Two of the fundamental issues for nonlinear PDEs(1.1)are the following:
(i)Weak Continuity and Rigidity:Let{Uε}ε>0be a sequence of exact solutions satisfying

Issue 1.1Does the limit function U satisfy

or

for a different nonlinear mappingassociated with the original nonlinear mapping N[·]and the solution sequence{Uε}ε>0?
Such an issue arises in rigidity problems in geometry,mechanics,among others.
(ii)Compactness and Convergence:Let{Uε}ε>0be a sequence of approximate or multiscale solutions satisfying
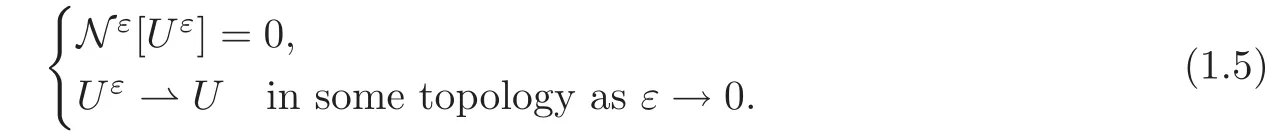
Issue 1.2Does the limit function U satisfy(1.3),or(1.4)for a different nonlinear mappingassociated with the nonlinear mappings Nε[·]and the solution sequence{Uε}ε>0?
This issue arises in the viscosity methods,relaxation methods,numerical methods,as well as problems for homogenization,hydrodynamic limits,and search for effective equations,among others.
This paper presents several examples of these fundamental problems involving weak continuity and compactness for nonlinear PDEs,in which compensated compactness and related ideas,developed by Luc Tartar[85–89]and Fran¸cois Murat[70–74],have played a significant role(see also[91]).In particular,in Section 2,we first analyze the compactness and convergence of vanishing viscosity solutions to hyperbolic conservation laws.In Section 3,we reveal the weak continuity and rigidity of the Gauss-Codazzi-Ricci system and corresponding isometric embeddings in differential geometry.Further references are also provided for some recent developments on the weak continuity and compactness for nonlinear PDEs.We finally remark that,as we will see in Sections 3–4,many fundamental problems in this direction are still open,which require further new mathematical ideas,techniques,and approaches that deserve our special attention.
2 Compactness and Convergence of Vanishing Viscosity Solutions to Hyperbolic Conservation Laws
Consider the following one-dimensional nonlinear hyperbolic conservation laws of the form:

where F:RN→RNis a nonlinear mapping so that all the eigenvalues of∇UF(U)are real.
To solve these nonlinear PDEs,one of the important approaches is the viscosity method for which one honors the physical or designs an artificial N×N matrix function as follows:
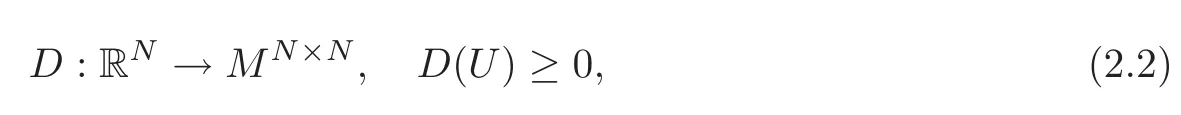
so that
(i) ∂tU+ ∂xF(U)= ε∂x(D(U)∂xU)admits a global solution Uε(t,x)for each fixed ε>0;
for general viscosity matrices D(U),including the Navier-Stokes viscosity matrices.This especially includes the fundamental problem in mathematical fluid dynamics,the inviscid limit of solutions of the Navier-Stokes equations to the Euler equations for homentropic flow via the BV-estimate,which is still open.
(ii)Decompose ∂xUεalong a suitable basis of unit vectors{r1,···,rN},
The idea of the vanishing viscosity method originates in the philosophy of regarding the inviscid gas as the limit of viscous gases,which can date back to the 19th century,including the works by Stokes(1848),Rankine(1870),Hugoniot(1889),Rayleigh(1910),Taylor(1910)and Weyl(1949),among others(see also[28]and the references cited therein).This idea has played an essential role in developing the mathematical theory of hyperbolic conservation laws(such as discontinuous solutions,entropy conditions,existence,uniqueness,and solution behavior),as well as numerical methods and related applications(such as shock capturing,upwind,and kinetic schemes).This method becomes increasingly important,especially for understanding the recently observed non-uniqueness phenomena for the weak solutions satisfying the entropy equality for the multidimensional Euler equations(see[29–30]).On the other hand,the realization of this method is truly challenging in mathematics,since it involves several fundamental difficulties in analysis,including singular limits,nonlinearity,discontinuity,singularity,oscillation,cavitation,and concentration.
目前临床上最常用的Humphrey视野检测程序为24-2或30-2,许多研究表明青光眼的神经结构损害出现在视野功能损害之前,且上述传统视野检查并不能检测出视野缺损,直到足够量的神经纤维丢失[1]。SAP中10-2程序对中心视野功能的评价相比经典的24-2程序具有其特点,10-2程序共有68个数据点,分布在视野中心10度范围内,且点点间距为2度;而24-2程序点点间距为6度,不如前者精细。Jung等[2]报道SWAP10-2程序能够发现24-2程序所忽略的早期青光眼患者的黄斑损害。
2.1 Compactness and convergence via BV-estimates
The same arguments also work for multidimensional scalar conservation laws(see[55,92]);see also[11]for scalar conservation laws with memory.
2.1.1 Scalar conservation laws
Consider the Cauchy problem for scalar conservation laws(N=1)as follows:

with the initial data U|t=0=U0∈BV∩L∞(R).It can be shown that there exists C independent of ε such that the viscous solutions Uε=Uε(t,x)of(2.3)satisfy
(i)Maximum principle:kUεkL∞ ≤ C;
(ii)BV-estimate:
几个保安冲出来,把贾鹏飞按在地上,用戒尺在他的屁股上抽了三十下。这戒尺是胡马强平时惩戒保安用的,今天在保安手上用起来格外得心应手,也把贾鹏飞抽得半天才站立起来,在保安虎视眈眈的淫威之下,他绝望地趔趄着离去。
1986年,法国医生Dargent 等[20]首创经阴式根治性子宫颈切除术(vaginal radical trachelectomy, VRT),使年轻子宫颈癌患者切除子宫颈可以保留子宫,仍然有生育功能。VRT手术可以使用在肿瘤直径<2 cm的患者,有人提出开腹手术(abdominal radical trachelectomy, ART)手术指征可以放宽至小于或等于4 cm的最大肿瘤直径,但仍然存在争议。
One of the approaches to achieve the BV-estimate is due to Vol’pert[92],which yields

in the sense of distributions,leading to the BV-estimate.
Then the compactness theorem in BV implies the strong convergence of Uε(t,x).
由表可见,W6盖梁施工作业中,R12作业人员失足高处坠落、R32防护不到位、R42施工粉尘(烟尘)、R13起重机械操作不当、R35临时用电不当、R33施工物品掉落为主要风险,其中R12高处坠落与R32防护不到位为高风险因素,需要特别注意.R42施工粉尘(烟尘)、R13起重机械操作不当、R35临时用电不当、R33施工物品掉落、R22起重机械故、R15焊接操作不当等也需要引起重视.
Similar arguments can yield the L1-equicontinuity of Uεdirectly,which is also a corollary of the L1-stability and the comparison principle via Kruzhkov’s method(see[55]).
This compactness framework is based on the compactness theorem in BV,which is a suffi cient framework to ensure the strong compactness and convergence of exact/approximate solutions.On the other hand,achieving the BV-estimates of exact/approximate solutions is usually very challenging for the nonlinear systems,even though it is relatively easier for the scalar case.
2.1.2 Hyperbolic systems of conservation laws:BV-estimate via Glimm’s approach
Glimm[41]first developed a random choice method,the Glimm scheme,and derived the BV-estimate of the corresponding Glimm approximate solutions,based on the Glimm functional and corresponding wave interaction estimates.The techniques developed have been successfully employed to establish the global existence of solutions in BV and analyze the behavior of solutions in BV(structure,uniqueness,stability,and asymptotic behavior of solutions in BV)when the total variation of the initial data is small(see also[28,33,42,61]and the references cited therein).
Theorem 2.1For a strictly hyperbolic system(2.1)on U in a neighborhood of a compact set K ⊂ RN,there exist constants δ>0 and C such that,if

then there exists a global solution U(t,x)such that

Glimm’s approach was further employed to handle the front-tacking method and developed to analyze the L1-stability of global solutions obtained by either the Glimm scheme or the front tracking method(see[5,28,50,58,62]and the references cited therein).The approach was also developed to analyze the well-posedness for two-dimensional steady supersonic Euler flows past a Lipschitz wedge in[16,25].
2.1.3 Hyperbolic systems of conservation laws:BV–estimate for the artificial viscosity method
印刷行业现在最缺的可能就是,数字化的人才,这类人才,不单要熟练操作数字化设备,还应娴熟运用各类数字化软件,李新立坦陈自己的忧虑。诚如他所说,传统印刷在国内经过这二十多年的大发展,已经储备了大量的人才,但在数字化的时代,一切应用都跟数据有关,行业及企业要想赢得未来,精通数字语言的人才就是关键。而如何破局,还需群策群力。
Consider the following Cauchy problem for one-dimensional nonlinear hyperbolic systems of conservation laws with vanishing artificial viscosity(i.e.,D(U)=IN×N):

and the initial data U(0,x)=U0(x)∈BV(RN).
Theorem 2.2(Bianchini-Bressan[4]) For a strictly hyperbolic system(2.1)on U in a neighborhood of a compact set K ⊂ RN,there exist constants δ>0 and Cj,j=1,2,3,such that,if U0satisfies(2.4),then,for any fixed ε>0,there exists a unique solutionof the Cauchy problem(2.5)such that
(i)BV bound:Tot.Var.Tot.Var.{U0};
(ii)L1-stability:
一般认为,高校教师肩负着教书育人、科学研究和社会服务三大任务。但三者绝非同等重要,相互分离,而是有主有次,彼此联系。就三者的主次地位而言,教学居首要地位。就三者的内在联系来看,教学是中心。

These imply the strong convergence and L1-stability of the limit solution to(2.1).
本文所倡导建立的敦煌文献多模态语料库并非单纯文本和图像的集合,我们还将开发该语料库的检索、维护和管理多功能系统,使其具备良好的存储、反馈、修正、检索、统计、分析、结果输出等性能,以便各领域研究人员都能从语料库中获取自己所需要的信息。其主要功能如图 2[12]24所示。
See[51,57,76]for the one-dimensional case,and[55,92]for the multidimensional case.
The strategies to achieve the BV-estimate include the following steps:
(i)Employ the heat kernel to estimate the solution for t∈ [0,τε],

where κ is small,independent of ε and δ.
This method for the multidimensional case can be analogously formulated.
∂xUε=(sum of gradients of viscous travelling waves).
(iii)Derive a system of N equations for these scalar components,
社会工作的增能理论和陆九渊的心学理论作为古今中外两种不同的理论肯定拥有巨大的区别,这一点是毋庸置疑的。但是经过比较,我们欣喜的发现,两种理论也同时具有多种重要的相似点。这意味着增能理论在中国传统主流思想中是有着些许对应的。这样我们在做增能理论本土化工作或增能理论本土实践工作的时候就有了可以凭借的本土思想资源。
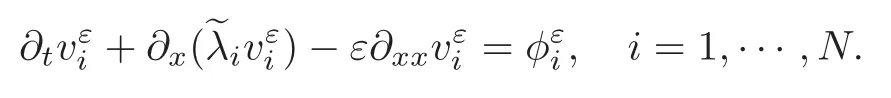
Then,as the scalar case,we obtain that,for all t≥ τε,

(iv)Construct the basis{r1,···,rN}in an appropriate way so that,for t≥ τε,
本文计算涡轮盘在0~100%转速循环下的低循环疲劳寿命,将螺栓孔处作为考核点,采用局部应力应变法并结合文献[3] 中平均应力、平均应变的计算方法,取螺栓孔处的应力、应变值带入式(3)中求得涡轮盘的疲劳寿命。具体计算结果如表3、表4所示。

which implies

whereand C are independent of ε>0.
Remark 2.1The results above still hold even for non-conservative strictly hyperbolic systems.On the other hand,this approach requires both the artificial viscosity(i.e.,D(U)=IN×N)and the total variation of the initial data sufficiently small.
Remark 2.2A longstanding open problem is the BV-estimate and convergence of vanishing viscosity approximation Uεgoverned by the general form as follows:

(ii)Uε(t,x)→ U(t,x)in some topology as ε→ 0,and U(t,x)is an entropy solution.
2.2 Compactness and convergence via compensated compactness
We now discuss the compactness and convergence of exact/approximate solutions to conservation laws via compensated compactness and related ideas,which only require much weak bounds that may be obtained easily through natural energy/entropy estimates as our examples below indicate.
充分提供情节背景下的学习是最有效的,语文学习的外延与生活的外延相等,生活的范围有多大,学习语文的范围就有多大。我们常常说的“生活即语文”正是这样的道理。
2.2.1 Scalar conservation laws
Consider the Cauchy problem for scalar conservation laws(2.3)(N=1)with the following initial data:

Then it can be easily shown that there exists C,independent of ε,such that the viscous solutions Uεsatisfy the following natural estimates:
为加强施工现场管理,江苏省出台了《江苏省重点水利工程建设管理规定》,按照规定要求,重点水利工程建设必须实行项目法人责任制、招标投标制、建设监理制、合同管理制和竣工验收制。在建设运行管理过程中,实现集中管理和分级管理相结合的体制。在现场施工管理工作中,全面落实现场管理的各项制度,抓好现场运行管理,保证工程建设有序地开展。
从习近平总书记关于党的群众路线的重要论述来看,可以看出习近平的理论贡献在他在遵循和继承马克思主义唯物史观的价值精髓的基础上,吸收了中国传统优秀政治文化的积极因素,创造性的提出了“以人民为中心的发展思想”,并从马克思主义政党同其他政党的本质区别出发论述了党的群众路线的政治意义和实践意义。他提出了“开展党的群众路线教育实践活动,就是要把为民务实清廉的价值追求深深植根于全党同志的思想和行动中”。〔13〕质言之,通过群众路线巩固党执政的基层基础,提升党的创造力、凝聚力、战斗力;通过群众路线构建“共建共治共享”治理过程,增强人民群众的获得感、幸福感和安全感。
(ii)Dissipation estimate:
The second estimate is a direct corollary of the natural energy estimate as follows:
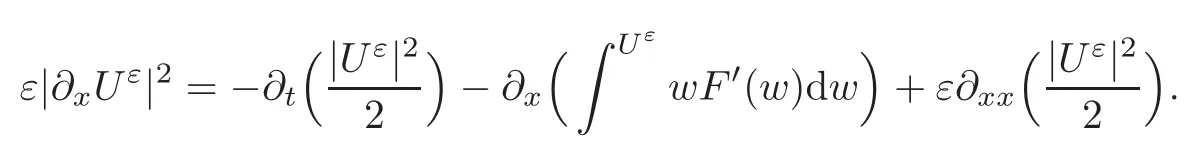
These estimates imply that,for any η ∈ C2with entropy flux
Then the compensated compactness arguments yield the weak continuity of F(Uε),or even the strong convergence of Uε(t,x)a.e.
For the convex case,Tartar[85]was the first to employ one entropy pair(η∗(U),q∗(U))=(U2,2RUwF′(w)dw)to conclude the strong convergence,which initiated the successful applications of compensated compactness to nonlinear hyperbolic conservation laws.For the nonconvex case,the entropy pairalso suffices to conclude the weak continuity with respect to the general equation,and the strong convergence when the equation is genuinely nonlinear for almost all U,as observed by Chen-Lu[18]and Luc Tartar independently.See also[36,80,84].
The approach also applies to(2.6)(N=1)with more general viscosity terms,as well as scalar conservation laws with memory(see[27]).
For these,the following div-curl lemma plays an essential role.
Lemma 2.1(see[70,85])Let Ω ⊂ Rd,d ≥ 2,be open bounded.Let p,q>1 such thatAssume that,for any ε>0,two vector fields
uε∈ Lp(Ω;Rd), vε∈ Lq(Ω;Rd)
satisfy the following:
(i)uε⇀ u weakly in Lp(Ω;Rd)as ε→ 0;
(i)Maximum principle:
(ii)vε⇀ v weakly in Lq(Ω;Rd)as ε→ 0;
(iii)divuεare conf i ned in a compact subset of
(iv)curlvεare conf i ned in a compact subset of
Then the scalar products of uεand vεare weakly continuous:
uε·vε→ u·v
in the sense of distributions.
Various variations of Lemma 2.1 for different applications/purposes were developed(see[6,91]and the references therein).
2.2.2 Hyperbolic systems of conservation laws:Compensated compactness for the artificial viscosity method
Consider(2.5)with artificial viscosity.Assume that there exists a strictly convex entropy function η∗(U),∇2η∗(U)>0.In many cases,it can be shown that there exists C independent of ε such that
(i)Invariant regions:
(ii)Dissipation estimate:
In fact,the dissipation estimate is natural as the scalar case,directly from the energy estimate as follows:
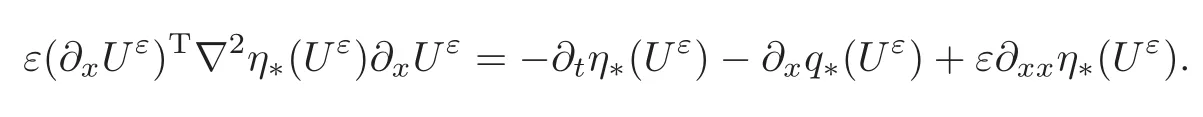
Then,for any η∈ C2with entropy flux q,i.e.,∇q(U)= ∇η(U)∇F(U),

The compensated compactness arguments can yield the strong convergence of Uε(t,x)when the system has strong nonlinearity.
The similar compensated compactness arguments apply to the systems with more general viscosity matrices(2.6)for∇2η∗(U)D(U)≥ c0>0.Another advantage of this approach is to allow the initial data of large oscillation without bounded variation.
In order to achieve the strong compactness,as first indicated by Tartar[85],combining the div-curl lemma(see[70,85])and the Young measure representation theorem(see[1,3,85]),we have the following commutation identity for the associated Young measure ν = ν(t,x)(λ)(probability measure)for the sequence Uε(t,x):
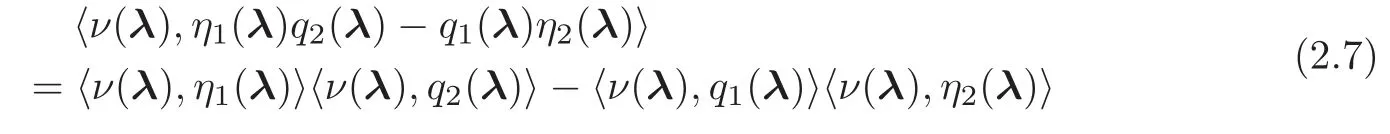
for any entropy pairs(ηj,qj),j=1,2,and
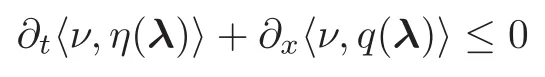
in the sense of distributions for any convex entropy pair(η,q),∇2η ≥ 0.Then the main mathematical issue is whether ν is a Dirac measure.The key point is the imbalance of regularity of the operator in the commutation identity,that is,the operator on the left is more regular than the one on the right due to cancellation when the system has strong nonlinearity.If so,the compactness of Uε(t,x)in L1follows.
For strict hyperbolicity with N=2,there are two families of entropy pairs determined by two arbitrary functions,which yield an affirmative answer to the issue(see[17,28,35,68,77,81]).
Further challenges include nonstrictly hyperbolic systems,viscosity matrices with
∇2η∗(U)D(U)≥ 0
but not positive definite,and initial data of large oscillation with only energy bounds(without bounded variation or L∞-uniform bound).We now start with a fundamental example of nonstrictly hyperbolic systems.
2.2.3 Homentropic Euler equations:Compensated compactness for the artificial viscosity method
The homentropic Euler equations take the following form:

where ρ is the density,is the fluid velocity that is well-defined when ρ >0,and p=p(ρ)= ρ2e′(ρ)is the pressure with internal energy e(ρ).
For a polytropic perfect gas,

where γ >1 is the adiabatic exponent,and the constant κ in the pressure-density relation may be chosen aswithout loss of generality.
One of the main difficulties for solving(2.8)is that strict hyperbolicity fails when ρ → 0.
An entropy function η(ρ,m)is called a weak entropy if η(ρ,m)|ρ=0=0.The weak entropy pairs can be represented as

for any C2-test function ψ(s),where χ(s)is the weak entropy kernel as follows:

The following mechanical energy-energy flux pair(η∗,q∗):

is a convex entropy pair for(2.8).
Consider the following homentropic Euler equations with artificial viscosity:

It can be shown for(2.12)that there exists C>0,independent of ε>0,such that
(i)Invariant regions for the L∞-estimate:

(ii)Dissipation estimate:
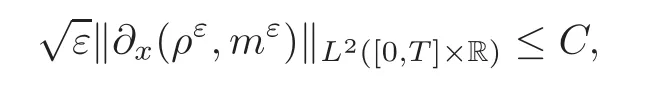
via the mechanical energy pair(η∗,q∗)that is strictly convex for 1< γ ≤ 2,and convex for γ>2 for which a corresponding weighted dissipation estimate can be obtained.
These estimates yield that,for any C2weak entropy pair(η,q),

Then the convergence problem for(ρε,mε)is reduced to the reduction problem for a measurevalued solution νt,xas follows.
Problem 2.1If suppνt,xis bounded,then

that is,(ρε(t,x),mε(t,x))→ (ρ(t,x),m(t,x))a.e.(t,x).
This problem was solved by DiPerna[34]forodd,Ding-Chen-Luo[31–32]and Chen[8]forLions-Perthame-Tadmor[64]for γ ≥ 3,Lions-Perthame-Souganidis[63]forand Chen-LeFloch[14]for general pressure laws.The key point is to employ effectively the weak entropy pairs in the commutation identity(2.7)for the associated Young measure νt,xwith compact support.
The convergence of related numerical methods with corresponding numerical viscosity matrices including the Lax-Friedrichs scheme and Godunov scheme was also established in[31–32](see also[10]).
The isothermal case γ=1 was also handled by Huang-Wang[52](see also[59]).
Some further important problems include the inviscid limit from the compressible Navier-Stokes equations to the compressible Euler equations(see Subsection 2.3)and the existence of global spherically symmetric solutions to the compressible Euler equations(see Subsection 2.4).
2.3 Navier-Stokes equations:Inviscid limit
Consider the following Cauchy problem:

with the initial conditions
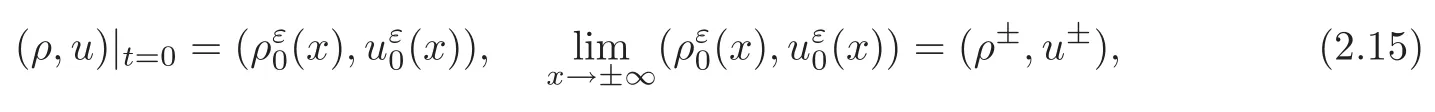
where(ρ±,u±)are constant end-states with ρ±>0,and the viscosity coefficient ε∈ (0,ε0]for some fixed ε0.
The existence of C2-solutions(ρε,uε)(t,x)for large initial data was obtained by Kanel[54]for the same ending states and by Hoff[48]for different ending states.
Inviscid Limit ProblemDoes the solution sequence(ρε,uε)(t,x)of(2.14)strongly converge to a solution to the homentropic Euler equations(2.8)when ε→ 0?
This problem was addressed by Gilbarg[40],Hoff-Liu[49],and Gùes-Métivier-Williams-Zumbrun[45]for some physical cases with special structures for which the limit solution contains only one shock.
For the general case,several new difficulties arise,which include
(i)No invariant regions:Only energy norms;
(ii)Direct derivative estimates only partially:
(iii)No a priori bounded support of the measure-valued solution νt,x.
Nevertheless,the following theorem has been established.
Theorem 2.3(Chen-Perepelitsa[19])Let the initial functionssatisfy

where Φ∗(ρ,m)= η∗(ρ,m)−η∗−is a pair of smooth monotone functions satisfying=(ρ±,u±)when ±x ≥ L0for some large L0>0,and both E0and E1are independent of ε.Let(ρε,mε),mε= ρεuε,be the solution of the Cauchy problem for the Navier-Stokes equations(2.14)for each fixed ε>0.Then,when ε→ 0,there exists a subsequence of(ρε,mε)that converges strongly almost everywhere to a fi nite-energy solution(ρ,m)to the Cauchy problem for the homentropic Euler equations(2.8)for any γ>1.
The strategies for this include the following steps:
(i)Derive the finite-energy bound and higher integrability bound(replacing L∞bound).
(ii)Derive a new derivative estimate for ε∂xρε.
(iii)Show the H−1-compactness of weak entropy dissipation measures only for weak entropy pairs with compactly supported C2-test functions.
(iv)Prove that any connected component of support of the measure-valued solution νt,xmust be bounded,which reduces to the case when the support of νt,xis bounded as in Subsection 2.2.3.
To achieve these,the following key estimates of solutions to the Navier-Stokes equations are essential:There exist C1>0 and C2=C2(E0,E1,K,γ,t)independent of ε for any compact set K⊂R such that,for any t>0,
(i)Energy estimate:

(ii)New derivative estimate for the density:
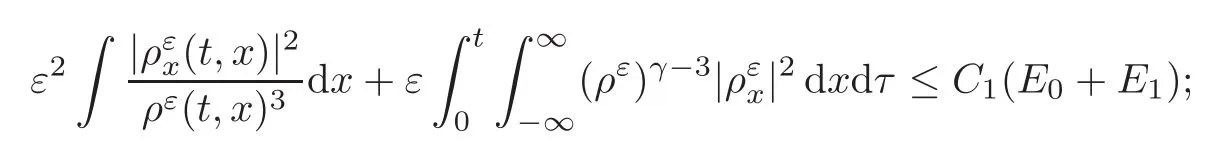
(iii)Higher integrability bound:
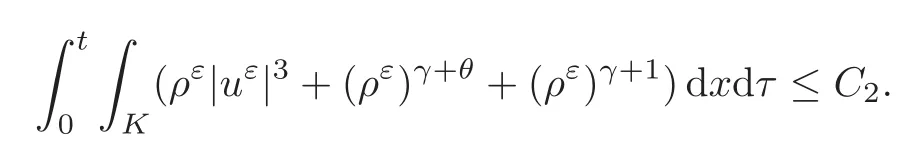
The higher integrability estimate(iii)is motivated by the related work by Lions-Perthame-Tadmor[64]and LeFloch-Westdickenberg[60].For some related earlier work on the convergence of approximate solutions in the Lp-framework,see[82]for a 2×2 system of elasticity with severe growth conditions,and[60]for the convergence of approximate solutions with full dissipation in the energy norms for the homentropic Euler equations with
Let νt,xbe the Young measure determined by the solutions of the Navier-Stokes equations(2.14).Then νt,xis conf i ned by

for the entropy kernelwithandwherehνt,x,f(s;ρ,u)i.
The goal is to establish that the Young measure is a Dirac mass in the phase plane for(ρ,m).The new difficulty is now that supp νt,xis unbounded in general.
We divide the proof into three cases.
Case 1γ =3.The same argument for the bounded support of νt,xapplies as in[64].In this case,θ=1 and the commutation relation becomes
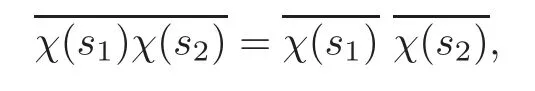
which impliesby taking s1=s2,that is,

This implies that ν must be a Dirac mass on the set{ρ >0}or be supported completely in the vacuum V={ρ =0},that is,the measure-valued solution νt,xis a Dirac mass(2.13)in the phase plane for(ρ,m).
Case 2γ >3.Let A:= ∪ {(u − ρθ,ρθ+u):(ρ,u)∈ suppν}.Let J=(s−,s+)be any connected component of A.Note that suppχ(s)={(ρ,u):u −ρθ≤ s≤ u+ρθ}.
Claim 2.1The connected component J is bounded for γ>3.
On the contrary,let inf{s:s∈J}= −∞.Our strategy is to fix M0first such that M0+1∈J and restrict s2∈(M0,M0+1),then choose sufficiently small s1≤−2|M0|to reach the contradiction.
To achieve this,two following estimates are essential:
(i)for λ <0,which is our key new observation.
(ii)a.e.s1,s2∈ J,s1 Combining the two estimates,we have which implies that,when s1→−∞, This arrives at the contradiction. The case when J is unbounded from above can be treated similarly. This indicates that any connected component J of the support of the Young measure ν is bounded for γ >3,which reduces to the Lions-Perthame-Tadmor’s case for γ >3 in[64]. Case 3γ∈(1,3).On the contrary,suppose that a connected component J of the support is unbounded from below. Let M0=sup{s:s∈ J}∈ (−∞,∞].Let s1,s2,s3∈ (−∞,M0)with s1 Differentiating this equation in s2and dividing by(s3−s1),we obtain Our strategy is to take s1→ −∞ first and then show that the left-hand side has a smaller order than the right-hand side to arrive at the contradiction. To do this,we divide the argument into five steps: (i)Show the estimate by employing Lions-Perthame-Tadmor’s argument in[64]. (ii)Show thatbut is not identically zero,andas s → inf J,supJ.This yields that there exists s2such thatand (iii)Let s3>s2be the points such thatand let s1→ −∞.From the first identity(2.16), (iv)Show that (v)From the second equation(2.17),by throwing away the negative terms,we have which implies This arrives at the contradiction as s1→−∞. Another different proof was given by LeFloch-Westdickenberg[60]forThe inviscid limit of the viscous shallow water equations to the Saint-Venant system was also established in[20]. The homentropic Euler equations for multidimensional compressible fluids take the following form: where x=(x1,···,xd)∈ Rd,∇xis the gradient with respect to x ∈ Rd,and v=(v1,···,vd)∈Rdis the velocity.The pressure-density constitutive relation(by scaling)satisfies(2.9). We seek the spherically symmetric solutions of the following form: Then the functions(ρ,m)=(ρ,ρu)are governed by For the defocusing case,the existence of expanding spherically symmetric solutions with the following bounds: has been constructed,provided that the initial functions have the same bounds in[9]. For the focusing case,the singularity of imploding self-similar spherically symmetric solutions was discussed in[26,44,79,93].It is indicated indeed in[78]that there is no BV or L∞bound for the imploding solutions in general. A longstanding open problem is whether the concentration phenomenon occurs at the origin,that is,whether the density ρ develops a measure at the origin.In[21],we developed a method of vanishing artificial viscosity to prove that the vanishing viscosity limit solution does not form concentration at the origin,but has a bounded total energy.More precisely,we construct a sequence of vanishing viscosity solutions to the following initial-boundary problem: with the appropriate approximate initial data and the boundary condition where(ρ0,m0)is the initial data for the spherical symmetric solution to(2.20),pδ(ρ)= δρ2+κργwith δ= δ(ε),and a(ε),b(ε),(ε)and δ(ε)are positive with(0,0),as well as certain combinations of(b(ε),(ε),δ(ε))tending to 0,as ε→ 0(see[21]).Then we have the following theorem. Theorem 2.4(Chen-Perepelitsa[21])Let the initial functions(ρ0,m0)for(2.20)satisfy the finite-energy conditions.Then (i)for sufficiently small fixed ε>0,there exists a global viscous solution(ρε,mε)to the initial-boundary value problem(2.21)–(2.23)satisfying that,for any compact set K ⊂ R+and T>0,there exists CT>0 independent of ε>0 such that,for any 0 (ii)when ε→0,there exists a subsequence of(ρε,mε)that converges strongly almost everywhere to a finite-energy spherically symmetric solution(ρ,m)to(2.20)for any γ >1 with the initial data(ρ0,m0). The key ingredients are the uniform a priori estimates in(i)in combination with the reduction of the corresponding Young measure discussed in Subsection 2.3. Recently,we have also solved and/or made progress on several fundamental problems in nonlinear partial differential equations by employing the viscosity method.These include the vanishing viscosity approximation for transonic flow in Chen-Slemrod-Wang[22](see also Morawetz[67,69]),and the subsonic-sonic limit of exact/approximate solutions to the full Euler equations for multidimensional steady compressible fluids in Chen-Huang-Wang[13]. The isometric embedding problem is a longstanding fundamental problem in differential geometry.As is well-known from differential geometry,given a surface,we can compute its metric{gij}and the associated first fundamental form and its curvatures are determined by the second fundamental form Then a natural mathematical question is as follows: Isometric Embedding ProblemGiven a metric{gij},can we find a surface in the Euclidean space with the given metric{gij}? In other words,we seek a map r:Ω→RNsuch that in the local coordinates,that is,so thati 6=j,in Rdare linearly independent. This is an inverse problem,which is a realization question for a given abstract metric{gij}.A further question is whether we can produce even more sophisticated surfaces or thin sheets for applications.These questions are truly fundamental,not only in mathematics such as differential geometry and topology,but also in many applications such as the understanding evolution of sophisticated shapes of surfaces or thin sheets in nature including elastic materials,protein folding in biology and algorithmic origami,as well as design and visual arts,among others. The mathematical study of this problem has a long history,including the early important works by Schlaef l i(1873),Darboux(1894),Hilbert(1901),Weyl(1916),Janet(1926–1927)and Cartan(1926–1927)(see also[47]and the references therein).In particular,Nash[75]established the Nash isometric embedding theorem(also called the Ck-embedding theorem,k≥3)as follows. Theorem 3.1Every n-dimensional Riemannian manifold(analytic or Ck,k≥3)can be Ck-isometrically imbedded in the Euclidean space Rdwith d=2sn+4n for the compact case and d=(n+1)(3sn+4n)for the noncompact case,whereis the Jenet dimension(see[53]). The results were further improved with lowerer target dimensions by Gromov[43]with d=sn+2n+3 and Günther[46]with d=max{sn+2n,sn+n+5}. The following further problems are important for applications: (i)Rigidity of isometric embeddings:Is a weak limit of a sequence of isometric embeddings in some topology still an isometric embedding? (ii)Lowerest target dimension for global isometric embeddings,which is expected to be the Janet dimension d=sn. (iii)Optimal or assigned regularity such as C1,1,W2,pand BV1. The regularity issue is quite sensitive.For example,Efimov’s example in[38]indicates that there is no C2-isometric embedding when n=2 and d=sn=3. For n=2 and d=3,the fundamental theorem in differential geometry indicates the following result. Theorem 3.2There exists a surface in R3whose first and second fundamental forms are I and II,if the coefficients{gij}and{hij}of the two given quadratic forms I and II,I being positive definite,satisfy the Gauss-Codazzi system.That is,given{gij},the second fundamental coefficients{hij}are determined by the Codazzi equations(compatibility)as follows: subject to the following Gauss equation(i.e.,the Monge-Ampère type constraint): where Γare the Christof f el symbols,depending on gijup to their first derivatives,and K(x,y)is the Gauss curvature,determined by gijup to their second derivatives. This theorem holds even when hij∈ Lp(see[65–66]).Note that(3.1)–(3.2)is a system of nonlinear PDEs of the mixed elliptic-hyperbolic type,which is determined by the sign of the Gauss curvature K.Surfaces with Gauss curvature of changing signs are very normal in geometry,including tori such as toroidal shells or doughnut surfaces. Fluid Dynamics Formalism for Isometric Embedding(Chen-Slemrod-Wang[23]).Set L= ρv2+p,M= −ρuv,N= ρu2+p and q2=u2+v2.Choose p as the Chaplygin type gas as follows: The Codazzi equations(3.1)become the following balance laws of momentum equations: and the Gauss equation becomes the Bernoulli relation Define the sound speed c2=p′(ρ).Then c2>q2and the“flow”is subsonic when K>0. c2 c2=q2and the“flow”is sonic when K=0. Based on this connection,the existence and continuity of isometric embeddings via compensated compactness and entropy analysis were first addressed in[23]. For higher-dimensional cases,the isometric embeddings of n-dimensional Riemannian manifolds(n≥3)into Rdare described by the following Gauss-Codazzi-Ricci system: Gauss equations Codazzi equations Ricci equations where{Rijkl}is the Riemann curvature tensor,andare the coefficients of the connection form(torsion coefficients)on the normal bundle;the indices a,b,c run from 1 to N,and i,j,k,l,m,n run from 1 to d≥3. The Gauss-Codazzi-Ricci system(3.3)–(3.5)has no type,neither purely hyperbolic nor purely elliptic for the general Riemann curvature tensor Rijkl(see[7]).However,we have established the following weak continuity and rigidity of(3.3)–(3.5)and the corresponding embedded surfaces. Theorem 3.3(Chen-Slemrod-Wang[24])Consider the Gauss-Codazzi-Ricci system(3.3)–(3.5). (i)Letbe a sequence of solutions to(3.3)–(3.5),which is uniformly bounded in Lp,p>2.Then the weak limit vector fieldof the sequencein Lpis still a solution to(3.3)–(3.5). (ii)There exists a minimizerfor the following minimization problem: where S is the set of weak solutions to(3.3)–(3.5). This weak continuity and rigidity theorem is a reminiscence of the polyconvexity theory in nonlinear elasticity by Ball[2],for which the rigidity of elastic bodies can be achieved. The proof of this theorem is based on the following observations on the div-curl structure of the Gauss-Codazzi-Ricci system: and Rj,j=1,2,···,8,are conf i ned in a compact set in Then employing the Murat-Tartar’s div-curl lemma directly yields in the sense of distributions as ε→ 0,which implies the weak continuity and rigidity of(3.3)–(3.5)and the corresponding isometric embeddings. A compactness framework for the Gauss-Codazzi-Ricci system(3.3)–(3.5)was established in[24]as follows:Given any sequence of approximate solutions to this system which is uniformly bounded in L2and has reasonable bounds on the errors made in the approximation(the errors are conf i ned in a compact subset ofthe approximating sequence has a weakly convergent subsequence whose limit is still a solution to(3.3)–(3.5). These results indicate that the weak limit of isometrically embedded surfaces is still an isometrically embedded surface in Rdfor any Riemann curvature tensor{Rijkl}without restriction,which is the rigidity property of embedded surfaces in geometry. AcknowledgementsThe materials presented above include direct and/or indirect contributions of the author’s collaborators Xiaxi Ding,Feimin Huang,Philippe LeFloch,Bang-He Li,Tianhong Li,Yunguang Lu,Peizhu Luo,Mikhail Perepelitsa,Marshall Slemrod,Dehua Wang,Tian-Yi Wang,Yongqian Zhang,Dianwen Zhu,among others. [1]Alberti,G.and Müller,S.,A new approach to variational problems with multiple scales,Comm.Pure Appl.Math.,54,2001,761–825. [2]Ball,J.M.,Convexity conditions and existence theorems in nonlinear elasticity,Arch.Rational Mech.Anal.,63,1976–1977,337–403. [3]Ball,J.M.,A version of the fundamental theorem for Young measures,Lecture Notes in Phys.,344,Springer-Verlag,Berlin,1989,207–215. [4]Bianchini,S.and Bressan,A.,Vanishing viscosity solutions of nonlinear hyperbolic systems,Ann.of Math.,161(2),2005,223–342. [5]Bressan,A.,Hyperbolic Systems of Conservation Laws:The One-Dimensional Cauchy Problem,Oxford University Press,Oxford,2000. [6]Briane,M.,Casado-Díaz,J.and Murat,F.,The div-curl lemma “trente ans aprs”:An extension and an application to the G-convergence of unbounded monotone operators,J.Math.Pures Appl.,91(9),2009,476–494. [7]Bryant,R.L.,Griffiths,P.A.and Yang,D.,Characteristics and existence of isometric embeddings,Duke Math.J.,50,1983,893–994. [8]Chen,G.Q.,Convergence of the Lax-Friedrichs scheme for isentropic gas dynamics(III),Acta Math.Sci.,6B,1986,75–120(in English);8A,1988,243–276(in Chinese). [9]Chen,G.Q.,Remarks on spherically symmetric solutions of the compressible Euler equations,Proc.Royal Soc.Edinburgh Ser.A,127,1997,243–259. [10]Chen,G.Q.,Euler Equations and Related Hyperbolic Conservation Laws,Handbook of Differential Equations:Evolutionary Differential Equations,Vol.2,C.M.Dafermos and E.Feireisl(eds.),Elsevier,Amsterdam,2005,1–104. [11]Chen,G.Q.and Christoforou,C.,Solutions for a nonlocal conservation law with fading memory,Proc.Amer.Math.Soc.,135(12),2007,3905–3915. [12]Chen,G.Q.,Dafermos,C.M.,Slemrod,M.and Wang,D.,On two-dimensional sonic-subsonic flow,Commun.Math.Phys.,271,2007,635–647. [13]Chen,G.Q.,Huang,F.M.and Wang,T.Y.,Subsonic-sonic limit of approximate solutions to multidimensional steady Euler equations,Arch.Rational Mech.Anal.,2015,to appear.arXiv:1311.3985 [14]Chen,G.Q.and LeFloch,P.G.,Compressible Euler equations with general pressure law,Arch.Rational Mech.Anal.,153,2000,221–259. [15]Chen,G.Q.and LeFloch,P.G.,Existence theory for the isentropic Euler equations,Arch.Rational Mech.Anal.,166,2003,81–98. [16]Chen,G.Q.and Li,T.H.,Well-posedness for two-diemnsonal steady supersonic Euler flows past a Lipschitz wedge,J.Diff.Eqs.,244,2008,1521–1550. [17]Chen,G.Q.,Li,B.H.and Li,T.H.,Entropy solutions in L∞for the Euler equations in nonlinear elastodynamics and related equations,Arch.Rational Mech.Anal.,170,2003,331–357. [18]Chen,G.Q.and Lu,Y.G.,The study on application way of the compensated compactness theory,Chinese Sci.Bull.,33,1988,641–644(in Chinese);34,1989,15–19(in English). [19]Chen,G.Q.and Perepelitsa,M.,Vanishing viscosity limit of the Navier-Stokes equations to the Euler equations for compressible fluid flow,Comm.Pure Appl.Math.,63,2010,1469–1504. [20]Chen,G.Q.and Perepelitsa,M.,Shallow water equations:Viscous solutions and inviscid limit,Z.Angew.Math.Phys.,63,2012,1067–1084. [21]Chen,G.Q.and Perepelitsa,M.,Vanishing viscosity solutions of the compressible Euler equations with spherically symmetry and large initial data,Comm.Math.Phys.,338,2015,771–800. [22]Chen,G.Q.,Slemrod,M.and Wang,D.,Vanishing viscosity method for transonic flow,Arch.Rational Mech.Anal.,189,2008,159–188. [23]Chen,G.Q.,Slemrod,M.and Wang,D.,Isometric immersions and compensated compactness,Comm.Math.Phys.,294,2010,411–437. [24]Chen,G.Q.,Slemrod,M.and Wang,D.,Weak continuity of the Gauss-Codazzi-Ricci system for isometric embedding,Proc.Amer.Math.Soc.,138,2010,1843–1852. [25]Chen,G.Q.,Zhang,Y.Q.and Zhu,D.W.,Existence and stability of supersonic Euler flows past Lipschitz wedges,Arch.Rational Mech.Anal.,181,2006,261–310. [26]Courant,R.and Friedrichs,K.O.,Supersonic Flow and Shock Waves,Springer-Verlag,New York,1948. [27]Dafermos,C.M.,Solutions in L∞for a conservation law with memory,Analyse Mathématique et Applications,Gauthier-Villars,Montrouge,1988,117–128. [28]Dafermos,C.M.,Hyperbolic Conservation Laws in Continuum Physics,Springer-Verlag,Berlin,2010. [29]De Lellis,C.and Székelyhidi,Jr.L.,On admissibility criteria for weak solutions of the Euler equations,Arch.Rational Mech.Anal.,195,2010,225–260. [30]De Lellis,C.and Székelyhidi,Jr.L.,The h-principle and the equations of fluid dynamics,Bull.Amer.Math.Soc.(N.S.),49,2012,347–375. [31]Ding,X.,Chen,G.Q.and Luo,P.,Convergence of the Lax-Friedrichs scheme for the isentropic gas dynamics(I)–(II),Acta Math.Sci.,5B,1985,483–500,501–540(in English);7A,1987,467–480;8A,1989,61–94(in Chinese). [32]Ding,X.,Chen,G.Q.and Luo,P.,Convergence of the fractional step Lax-Friedrichs scheme and Godunov scheme for the isentropic system of gas dynamics,Comm.Math.Phys.,121,1989,63–84. [33]DiPerna,R.J.,Decay of solutions of hyperbolic systems of conservation laws with a convex extension,Arch.Rational Mech.Anal.,64,1977,1–46. [34]DiPerna,R.J.,Convergence of the viscosity method for isentropic gas dynamics,Commun.Math.Phys.,91,1983,1–30. [35]DiPerna,R.J.,Convergence of approximate solutions to conservation laws,Arch.Rational Mech.Anal.,82,1983,27–70. [36]DiPerna,R.J.,Measure-valued solutions to conservation laws,Arch.Rational Mech.Anal.,88,1985,223–270. [37]DiPerna,R.J.,Compensated compactness and general systems of conservation laws,Trans.Amer.Math.Soc.,292,1985,383–420. [38]Efimov,N.V.,The impossibility in Euclideam 3-space of a complete regular surface with a negative upper bound of the Gaussian curvature,Dokl.Akad.Nauk SSSR(N.S.),150,1963,1206–1209;Soviet Math.Dokl.,4,1963,843–846. [39]Evans,L.C.,Weak Convergence Methods for Nonlinear Partial Differential Equations,CBMS-RCSM,Vol.74,A.M.S.,Providence,RI,1990. [40]Gilbarg,D.,The existence and limit behavior of the one-dimensional shock layer,Amer.J.Math.,73,1951,256–274. [41]Glimm,J.,Solutions in the large for nonlinear hyperbolic systems of equations,Comm.Pure Appl.Math.,18,1965,697–715. [42]Glimm,J.and Lax,P.D.,Decay of solutions of systems of hyperbolic conservation laws,Bull.Amer.Math.Soc.,73(105),1967. [43]Gromov,M.,Partial Differential Relations,Springer-Verlag,Berlin,1986. [44]Guderley,G.,Starke kugelige und zylindrische Verdichtungsstosse inder Nahe des Kugelmittelpunktes bzw,der Zylinderachse.Luftfahrtforschung,19(9),1942,302–311. [45]Guès,C.M.I.O.,Métivier,G.,Williams,M.and Zumbrun,K.,Navier-Stokes regularization of multidimensional Euler shocks,Ann.Sci.École Norm.Sup.,39(4),2006,75–175. [46]Günther,M.,Zum Einbettungssatz von J.Nash[On the embedding theorem of J.Nash],Math.Nachr.,144,1989,165–187(in German). [47]Han,Q.and Hong,J.X.,Isometric Embedding of Riemannian Manifolds in Euclidean Spaces,A.M.S.,Providence,RI,2006. [48]Hoff,D.,Global solutions of the equations of one-dimensional,compressible flow with large data and forces,and with differing end states,Z.Angew.Math.Phys.,49,1998,774–785. [49]Hoff,D.and Liu,T.P.,The inviscid limit for the Navier-Stokes equations of compressible,isentropic flow with shock data,Indiana Univ.Math.J.,38,1989,861–915. [50]Holden,H.and Risebro,N.H.,Front Tracking for Hyperbolic Conservation Laws,Springer-Verlag,New York,2011. [51]Hopf,E.,The partial differential equation ut+uux=uxx,Comm.Pure Appl.Math.,3,1950,201–230. [52]Huang,F.and Wang,Z.,Convergence of viscosity solutions for isothermal gas dynamics,SIAM J.Math.Anal.,34,2002,595–610. [53]Janet,M.,Sur la possibilitde plonger un espace Riemannian donndans un espace Euclidien,Ann.Soc.Pol.Math.,5,1926,38–43. [54]Kanel,I.,On a model system of equations for one-dimensional gas motion,Diff er.Uravn.,4,1968,721–734. [55]Kruzkov,S.N.,First order quasilinear equations with several independent variables,Mat.Sb.(N.S.),81(123),1970,228–255(in Russian). [56]Lax,P.D.,Shock wave and entropy,Contributions to Functional Analysis,E.A.Zarantonello(ed.),Academic Press,New York,1971,603–634. [57]Lax,P.D.,Hyperbolic Systems of Conservation Laws and the Mathematical Theory of Shock Waves,CBMS Regional Conference Series in Mathematics,11,SIAM,Philadelphia,1973. [58]LeFloch,P.G.,Hyperbolic Systems of Conservation Laws:The Theory of Classical and Nonclassical Shock Waves,Birkhäuser-Verlag,Basel,2002. [59]LeFloch,P.G.and Shelukhin,V.,Symmetries and local solvability of the isothermal gas dynamics equations,Arch.Rational Mech.Anal.,175,2005,389–430. [60]LeFloch,P.G.and Westdickenberg,M.,Finite energy solutions to the isentropic Euler equations with geometric effects,J.Math.Pures Appl.,88,2007,386–429. [61]Liu,T.P.,Admissible solutions of hyperbolic conservation laws,Mem.Amer.Math.Soc.,30,1981,240. [62]Liu,T.P.and Yang,T.,Well-posedness theory for hyperbolic conservation laws,Comm.Pure Appl.Math.,52,1999,1553–1586. [63]Lions,P.L.,Perthame,B.and Souganidis,P.E.,Existence and stability of entropy solutions for the hyperbolic systems of isentropic gas dynamics in Eulerian and Lagrangian coordinates,Comm.Pure Appl.Math.,49,1996,599–638. [64]Lions,P.L.,Perthame,B.and Tadmor,E.,Kinetic formulation of the isentropic gas dynamics and psystems,Comm.Math.Phys.,163,1994,415–431. [65]Mardare,S.,The fundamental theorem of surface theory for surfaces with little regularity,J.Elasticity,73,2003,251–290. [66]Mardare,S.,On Pfaf fsystems with Lpcoefficients and their applications in differential geometry,J.Math.Pure Appl.,84,2005,1659–1692. [67]Morawetz,C.S.,On a weak solution for a transonic flow problem,Comm.Pure Appl.Math.,38,1985,797–818. [68]Morawetz,C.S.,An alternative proof of DiPerna’s theorem,Comm.Pure Appl.Math.,44,1991,1081–1090. [69]Morawetz,C.S.,On steady transonic flow by compensated compactness,Methods Appl.Anal.,2,1995,257–268. [70]Murat,F.,Compacitpar compensation,Ann.Scuola Norm.Sup.Pisa Sci.Fis.Mat.,5,1978,489–507. [71]Murat,F.,Compacitpar compensation,II,Proceedings of the International Meeting on Recent Methods in Nonlinear Analysis(Rome,1978),Pitagora,Bologna,1979,245–256(in French). [72]Murat,F.,L’injection du ĉone positif de H−1dans W−1,qest compacte pour tout q<2,J.Math.Pures Appl.,60(9),1981,309–322(in French). [73]Murat,F.,Compacitpar compensation:Condition ncessaire et suffisante de continuitfaible sous une hypothse de rang constant,Ann.Scuola Norm.Sup.Pisa Cl.Sci.(4),8(1),1981,69–102(in French). [74]Murat,F.,A survey on compensated compactness,Contributions to Modern Calculus of Variations(Bologna,1985),Pitman Res.Notes Math.Ser.,148,Longman Sci.Tech.,Harlow,1987,145–183. [75]Nash,J.,The imbedding problem for Riemannian manifolds,Ann.Math.,63(2),1956,20–63. [76]Oleinik,O.A.,Discontinuous solutions of non-linear differential equations,Usp.Mat.Nauk.,12,1957,3–73;English translation:AMS Translations,Ser.II,26,95–172. [77]Perthame,B.and Tzavaras,A.E.,Kinetic formulation for systems of two conservation laws and elastodynamics,Arch.Rational Mech.Anal,155,2000,1–48. [78]Rauch,J.,BV estimates fail for most quasilinear hyperbolic systems in dimension greater than one,Comm.Math.Phys.,106,1986,481–484. [79]Rosseland,S.,The Pulsation Theory of Variable Stars,Dover Publications,New York,1964. [80]Schonbek,M.E.,Convergence of solutions to nonlinear dispersive equations,Comm.Partial Diff.Eqs.,7,1982,959–1000. [81]Serre,D.,La compacitpar compensation pour les systmes non linaires de deux equations a une dimension d’espace,J.Math.Pures Appl.,65,1987,423–468. [82]Serre,D.and Shearer,J.W.,Convergence with physical viscosity for nonlinear elasticity,preprint,1994(unpublished). [83]Smoller,J.,Shock Waves and Reaction-Diffusion Equations,2nd edition,Springer-Verlag,New York,1994. [84]Tadmor,E.,Rascle,M.and Bagnerini,P.,Compensated compactness for 2D conservation laws,J.Hyper.Diff.Eqs.,2,2005,697–712. [85]Tartar,L.,Compensated compactness and applications to partial differential equations,Research Notes in Mathematics,Nonlinear Analysis and Mechanics,Herriot-Watt Symposium,Vol.4,R.J.Knops(ed.),Pitman Press,Boston,1979. [86]Tartar,L.,The compensated compactness method applied to systems of conservation laws,Systems of Nonlinear Partial Differential Equations(Oxford,1982),NATO Adv.Sci.Inst.Ser.C Math.Phys.Sci.,111,Reidel,Dordrecht,1983,263–285. [87]Tartar,L.,Compacitpar compensation:Résultats et perspectives,Nonlinear Partial Differential Equations and Their Applications,Collge de France Seminar(Paris,1981/1982),Vol.IV,350–369,Res.Notes in Math.,84,Pitman,Boston,1983(in French). [88]Tartar,L.,Oscillations in nonlinear partial differential equations:Compensated compactness and homogenization,Nonlinear Systems of Partial Differential Equations in Applied Mathematics,Part 1(Santa Fe,N.M.,1984),243–266,Lectures in Appl.Math.,23,A.M.S.,Providence,RI,1986. [89]Tartar,L.,Discontinuities and oscillations,Directions in Partial Differential Equations(Madison,1985),Publ.Math.Res.Center Univ.Wisconsin,54,Academic Press,Boston,1987,211–233. [90]Tartar,L.,From Hyperbolic Systems to Kinetic Theory:A Personalized Quest,Lecture Notes of the Unione Matematica Italiana,6,Springer-Verlag,Berlin;UMI,Bologna,2008. [91]Tartar,L.,The General Theory of Homogenization:A Personalized Introduction,Lecture Notes of the Unione Matematica Italiana,7,Springer-Verlag,Berlin;UMI,Bologna,2009. [92]Vol’pert,A.I.,Spaces BV and quasilinear equations,Mat.Sb.(N.S.),73(115),1967,255–302(in Russian). [93]Whitham,G.B.,Linear and Nonlinear Waves,John Wiley and Sons,New York,1974. [94]Yau,S.T.,Review of geometry and analysis,Mathematics:Frontiers and Perspectives,International Mathematics Union,V.Arnold,M.Atiyah,P.Lax and B.Mazur(eds.),A.M.S.,Providence,RI,2000,353–401.






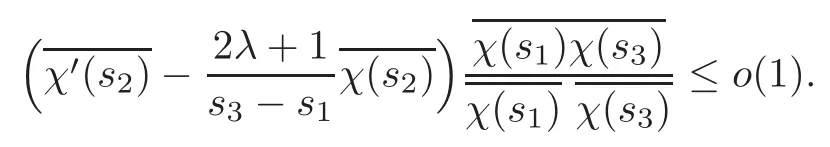
2.4 Spherically symmetric solutions to the multidimensional homentropic Euler equations




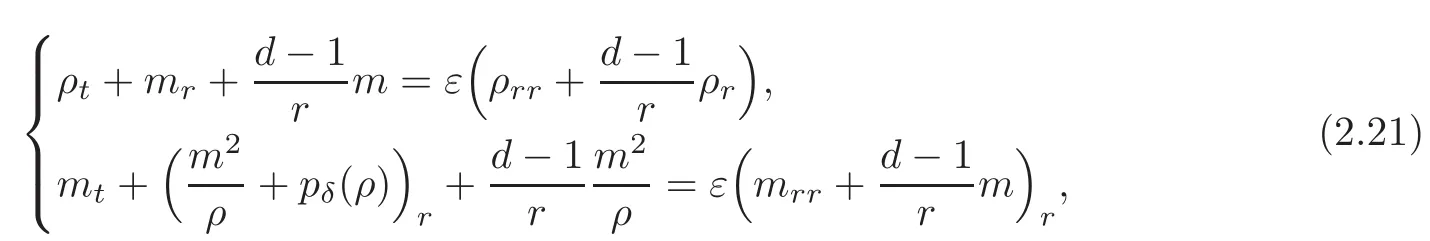
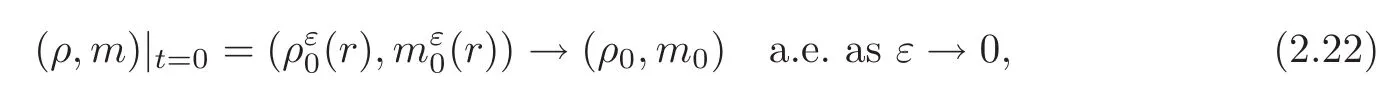

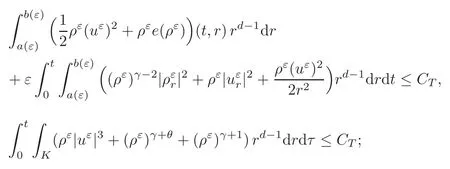
3 Weak Continuity and Rigidity of the Gauss-Codazzi-Ricci System and Corresponding Isometric Embeddings
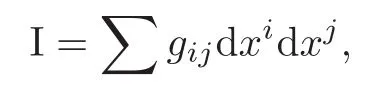

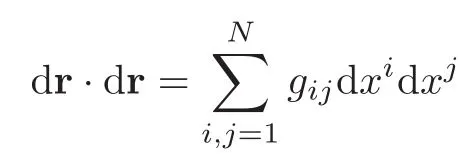









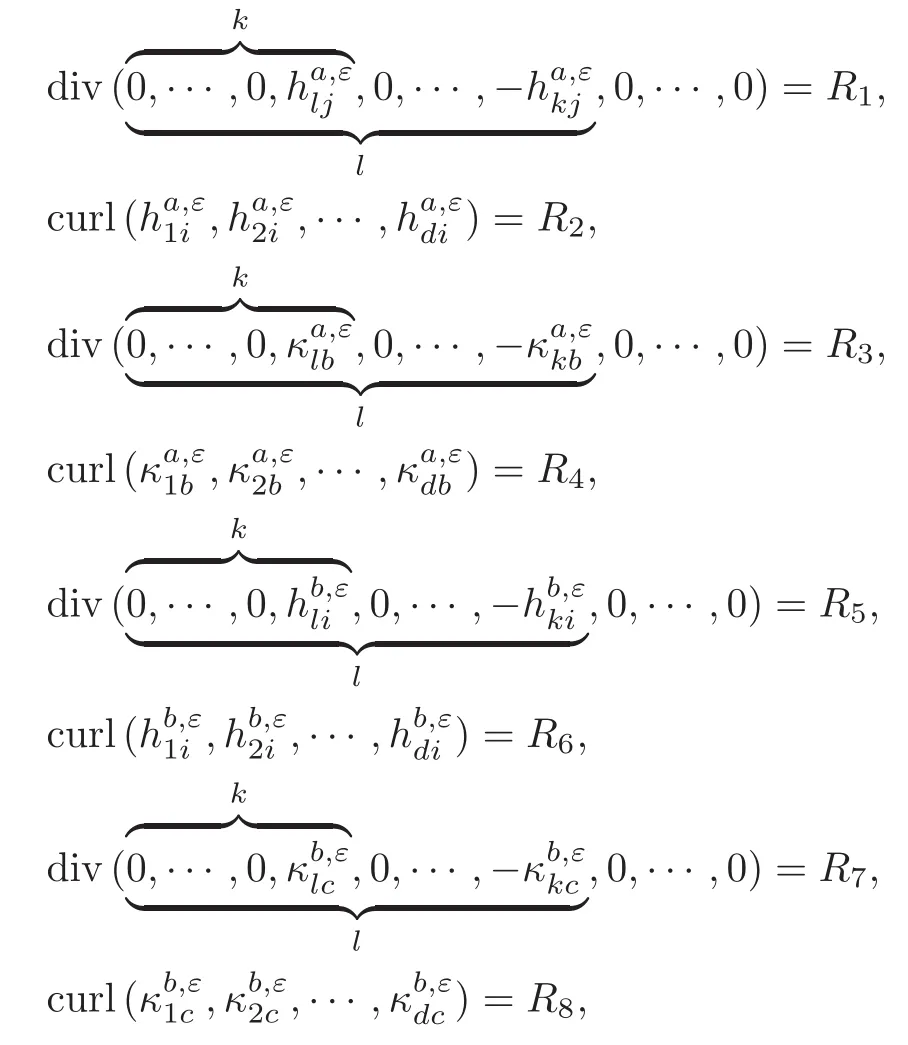

 Chinese Annals of Mathematics,Series B2015年5期
Chinese Annals of Mathematics,Series B2015年5期
