Some Smoothness Results for Classical Problems in Optimal Design and Applications∗

Juan CASADO-DAZ

(In Honor of the Scientific Contributions of Professor Luc Tartar)

1 Introduction

This paper deals with a classical problem in optimal design.It consists in mixing two isotropic materials(such as electric,thermic,···)given by their respective diffusion constants in order to minimize a certain functional.In other words,given a bounded open set Ω⊂RN,two constants 0<α<β and a distribution f∈H−1(Ω),we are interested in the problem

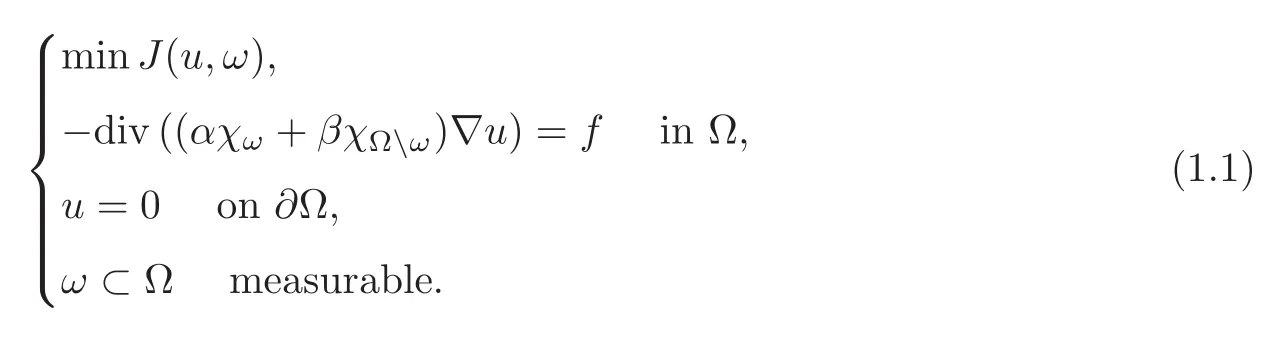
Here the control variable is the set ω,where we place the material α.In some interesting situations,one of the materials α or β is better than the other one but also more expensive.Then,it is usual to add to the above problem a bound on the amount of the best material.This type of problems has been considered since the pioneering works of Murat and Tartar.In particular,it is known that there is not a solution in general(see[13–14]).So,it is better to consider a relaxed formulation.This can be done by using the homogenization theory whose aim is to describe what materials can be approximated by using microscopic(or better mesoscopic)mixtures of other ones.Then,to relax(1.1),the idea is to consider the closure of the materials of the form αχω+β(1−χΩ)in the sense of the homogenization.We refer,for example,to[1,15,18,20,23]for the theoretical study of the homogenization theory and to[1,3,16,21–22]for its application to optimal design problems.

An interesting question from both the theoretical and numerical points of view is to study the smoothness properties of the solutions of(1.1)in its relaxed form.This is the problem that we consider in this paper for two very particular cases of functional J corresponding to

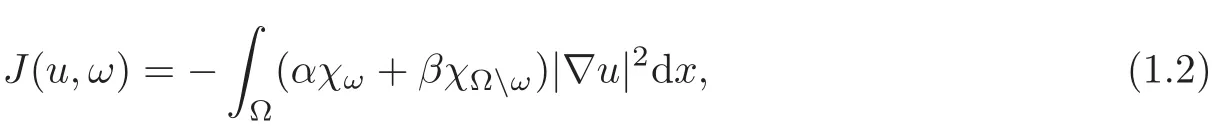
The case where J is given by(1.2),compliance problem,is considered in Section 2.It was specially studied for f=1 and N=2(see[9–10,16]),where the problem applies to maximizing the torsional rigidity of a rod and to maximizing the flow rate corresponding to two fluids of different viscosities in a pipe.Most of the results contained in these papers easily generalize to an arbitrary f.It is simple to check that the solution of(1.1)corresponds to ω = Ω,i.e.,material β is better than the material α.Thus,we will add the restriction|ω|≤ κ with 0< κ <|Ω|.Then,the problem has not a solution in general,and it is necessary to consider a relaxed formulation.It consists in replacing the materials(αχω+ βχΩω)by those of the form,where θ∈ L∞(Ω;[0,1])represents the proportion of material α which we are using in the homogenized mixture.As it is proved in[16],although an optimal solutionis not necessarily unique,the fluxis unique.Moreover,there existssuch thatIn this paper,we show that if Ω and f are smooth enough thenbelongs tois derivable in the orthogonal directions of,that is,is in L2(Ω)for 1≤i≤j≤N.This allows us to improve some results in[16],where they were established by assuming the existence of solutions to be smooth enough.

In Section 3,we consider the case where the functional J is given by(1.3).From the application point of view,it consists in minimizing the potential energy for an electric material or a membrane.In this case,the best material is β,and then we will add the restriction|ω|≥ κ with 0< κ <|Ω|.The relaxed formulation consists in replacing the materials(αχω+ βχΩω)by those of the form θα +(1 − θ)β,with θ∈ L∞(Ω;[0,1])being the proportion of material α in the homogenized mixture.For this problem,we show that ifis an optimal solution,thenis unique and there existssuch thatandMoreover,if Ω and f are smooth enough thenandis derivable in the directions of∇,that is,

In Section 4,we show that the results obtained in Section 2 can be applied to another classical problem in optimal design consisting in minimizing the first eigenvalue of the operator

In particular,our smoothness results allow us to obtain an example where the unrelaxed problem has not a solution.

The results in this paper are a summary of the ones in[4–5],where we can find the corresponding proofs.

2 The Compliance Problem

For a bounded open set Ω,three constants α,β,κ with 0< α < β,0< κ <|Ω|,and a distributionwe consider the compliance problem

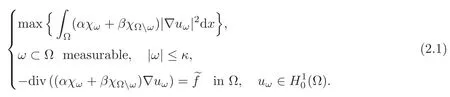
This problem has not a solution in general(see[13–14]),and therefore it is more convenient to work with a relaxed formulation which can be obtained(see[16,21–23])by replacing in(2.1)the materials of the form αχω+ βχΩωwith ω ⊂ Ω measurable by more general materials of the form

Here θ∈ L∞(Ω;[0,1])represents the proportion of material α in the homogenized mixture.Then,denoting

we get the following relaxed formulation for(2.1):

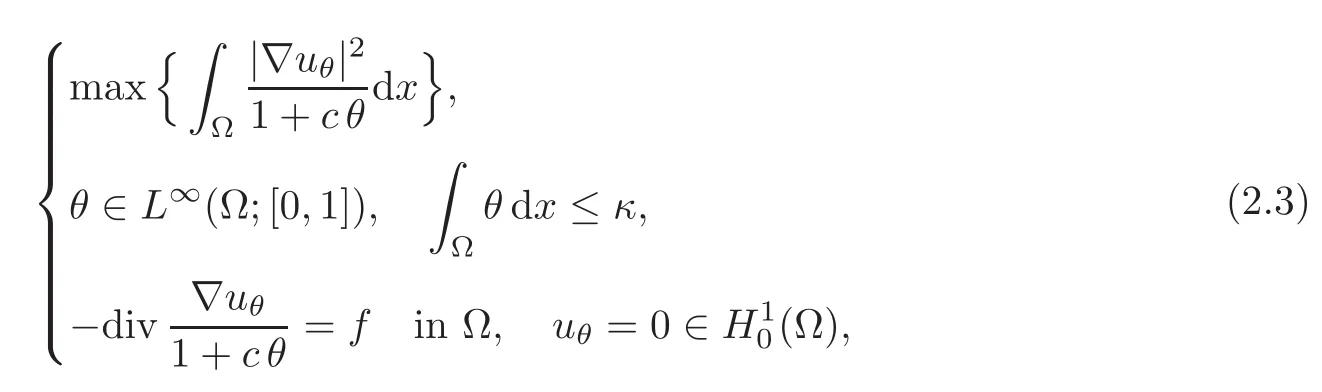
which by using the classical characterization of the state equation as a minimum problem can also be written as

The solution θ of(2.4)is not unique in general,but one can show the following result(see[16]).

Theorem 2.1There exists a unique functionsuch that for every solution(2.3),we have

This functionis characterized as the unique solution of

Moreover,is a solution of(2.3)if and only if it is a solution of

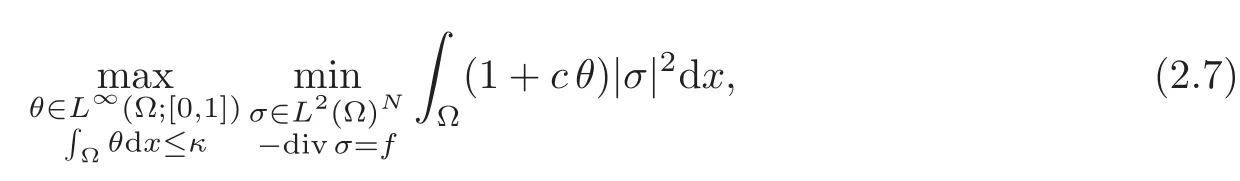
and the minimum in σ foris attained in.

Using the Kuhn-Tucker theorem to solve the minimum problem in θ in(2.6),we get the following theorem.

Theorem 2.2Define∈L2(Ω)Nby Theorem 2.1,andby

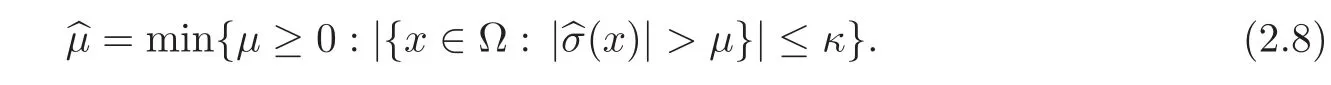
Then,every solutionof(2.3)satisfies

From(2.9),(2.5)and −divσ =f in Ω,we can also prove the following result which is the basis of our smoothness results for(2.3).We refer to[9]for a very related result.

Theorem 2.3Forgiven by(2.8),we define the positive convex function F∈W2,∞(0,+∞)by

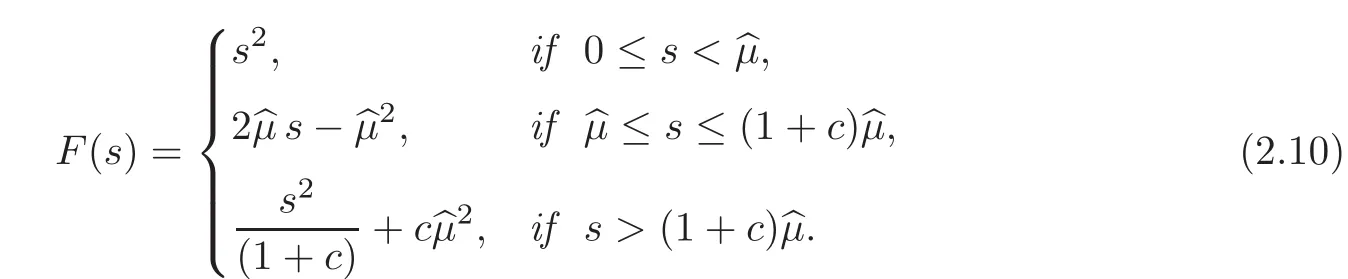
Then,if∈L∞(Ω;[0,1])is a solution of(2.3),the corresponding functionis a solution of

Moreover,can be obtained fromby

Using Theorem 2.3,we can now prove the following theorem.

Theorem 2.4Assume Ω ∈ C1,1,and defineby Theorem 2.2.We have the following assertions:

(1)If f ∈ W−1,p(Ω),2 ≤ p< ∞,thenbelongs to Lp(Ω)N.

(2)If f ∈ Lp(Ω),p>N,thenbelongs to L∞(Ω)N.

(3)If f∈W1,1(Ω)∩L2(Ω),thenbelongs to H1(Ω)Nand every solutionof(2.3)is such thatbelongs to L2(Ω),1≤i,j≤N.

Sketch of the ProofIt is based on Theorem 2.3.In other words,if F was C2with a strictly positive second derivative,then it is known that f being smooth implies that the solutions of(2.11)are twice derivable(see[8]).Using this result,the idea is then to approximate F for a sequence of smooth functions Fεstrictly convex.The solution uεof(2.11)with F replaced by Fεis twice derivable,and for a subsequence,converges to a solution u of(2.11)inNow,it is easy to check that∇∂iuεsatisfies an elliptic problem of the type

Although the matrix functions Mεare uniformly bounded,they lose the strict positivity when ε tends to zero,due to F not strictly convex.For this reason,we can not deduce the estimate that kD2uεkL2(Ω)N×Nis bounded.However,we can prove that Mε∇∂iuε·∇∂iuεis bounded in L1(Ω).Using the explicit expression of the matrix functions Mε,this allows us to show thatis in H1(Ω)N.The estimates of b σ in Lq(Ω)Nmainly follow from Stampacchia estimates(see[19]).

Remark 2.1The estimates in Theorem 2.4 are local.That is,if U is an open set in RNsuch that∂Ω∩U is in C1,1,then the results above hold with Ω replaced by Ω∩O and O ⊂⊂ U open.

Remark 2.2The fact thatis a solution of(2.3)and f∈Lp(Ω)(p>N)implies that the corresponding state functionis in W1,∞(K)for every compact set K⊂ Ω is given in[10]as a simple consequence of the results in[6].Therefore the main contribution of Theorem 2.4 refers to the estimates on the boundary and specially to∈ H1(Ω)N.

Theorem 2.4 has some interesting consequences for the unrelaxed problem(2.1).They apply mainly to proving the non-existence of a solution.

Theorem 2.5Assume Ω ∈ C1,1and f ∈ W1,1(Ω)∩L2(Ω).We suppose that there exists a solutionof(2.1)and defineby Theorem 2.1.Then,we have the following assertions:

(1)The curl ofis zero.

(2)If Ω is simply connected,then= ∇w,with w being the solution of

Remark 2.3The second assertion in the previous lemma was obtained in[16]assuming that the solutionhas a smooth boundary.Here the result is a consequence of Theorem 2.4.

Since curl=0,it is locally the gradient of a function w which,taking into account that−div=f,satisfies the equation −∆w=f(the second assertion of Theorem 2.5 is a consequence of this result).This allows us to prove that iff is in a certain space Wk,p(Ω),thenis in

3 The Energy Problem

In this section,instead of maximizing the functional in(2.1),let us minimize it.Now,the best material is not α but β.For this reason,we do not ask the measure of ω to be small but large.In other words,given a bounded open set Ω,two constants α, β,with 0< α < β,a distribution∈ H−1(Ω),and a constant κ with 0< κ <|Ω|,let us consider the problem

As for the compliance problem,it is better to work with a relaxed formulation,because problem(3.1)has not a solution in general.This relaxation can be obtained by replacing the materials of the form αχω+ βχΩωby those of the form αθ+ β(1 − θ)(see[1,16,21–23]).Taking

we then get the relaxed formulation of(3.1)

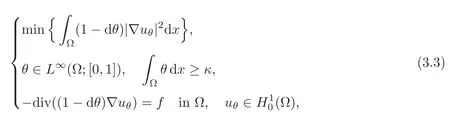
or equivalently

Instead of using the variables u and θ,it is also possible to write the problem in the variables σ and θ with σ =(1 − d)∇u,that is,(3.3)is also equivalent to

Remark that the structure of these problems is similar to those of(2.4)and(2.6),but the roles of σ and ∇u are exchanged.Thus we expect to prove properties similar to those obtained for the optimalin the compliance problem for the gradient of an optimal state function ū corresponding to the energy problem.This is what the results we state below essentially show.

We start with the following uniqueness result for(3.3).

Theorem 3.1There exists a unique functionsuch that ifis a solution of(3.3),then the corresponding state equationagreees with b u.Moreover,defining

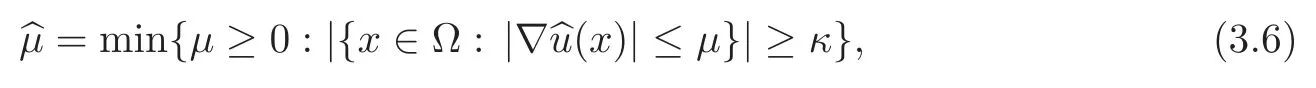
we have

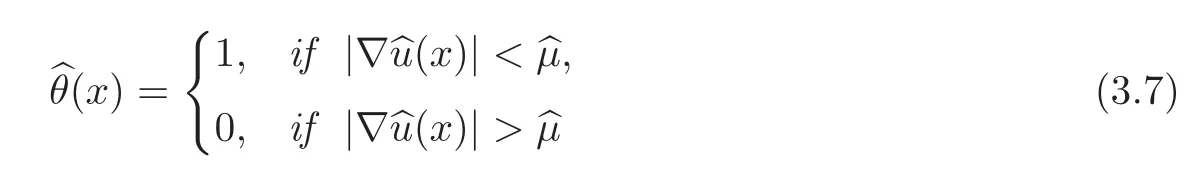
for every solutionof(3.3).

Analogous to Theorem 2.3 for(2.3),the following result is the key ingredient to obtaining some smoothness properties for the solutions of(3.3).

Theorem 3.2Letandbe given by Theorem 3.1.We define G∈W2,∞(0,+∞)by

Then,a function∈L∞(Ω)is a solution of(3.3)if and only if

is a solution of

Moreover,the functioncan be obtained fromby

Our main result related to the smoothness properties of the solutions of(3.3)is given by the following theorem.

Theorem 3.3Assume Ω∈C1,1,and defineby Theorem 3.1.Then,we have the following assertions:

(1)If f∈W−1,p(Ω),p≥2,thenbelongs to

(2)If f ∈ Lp(Ω),p>N,thenbelongs to W1,∞(Ω)N.Besides,if N=2,then

(3)If f∈L2(Ω),thenbelongs to H2(Ω),and every solutionof(3.3)is such that

Sketch of the ProofAs in the proof of Theorem 2.5,the idea is to approximate problem(3.10)by another one obtained by regularizing the function G defined by(3.8),which allows to construct a sequence of smooth functions uεconverging to û at least in H1(Ω).The second derivatives of uεsatisfy an elliptic equation of the form

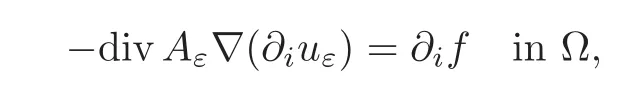
where,contrary to(2.13),the matrix functions Aεare uniformly elliptic and independent of ε,but they have not any upper bound.The proof of∈ H2(Ω)follows from this ellipticity condition,while the estimate in W1,∞(Ω)follows from Stampacchia estimates.In the special case N=2,we can show thatis in C1(Ω)by using the results in[2](see also[7,12]).

Remark 3.1Because in the proof of Theorem 2.5,we deal with a diffusion coefficient matrix bounded but not strictly elliptic and in Theorem 3.3 with a diffusion coefficient matrix strictly elliptic but unbounded,there are important differences in the proofs.Moreover,there are also some important differences in the result.In this sense,contrary to Theorem 3.3,we do not know whether the estimates in Theorem 3.3 are local,i.e.,whether Ω is smooth just in a portion of the boundary,we do not know whetheris smooth in a neighborhood of this portion.

Remark 3.2In Theorem 3.3,we proved that the optimal solutionsof(2.3)are derivable in the orthogonal directions toand then to∇.For 3.3,we have thatis derivable in the direction of

We finish this section by giving some consequences of Theorem 3.3 when it applies to the unrelaxed problem(3.1).

Theorem 3.4Assume Ω ∈ C1,1and f ∈ L2(Ω).We suppose that there exists a solution⊂Ω of(3.1)and de fineby Theorem 3.1.Then,we have the following assertions:

(1)

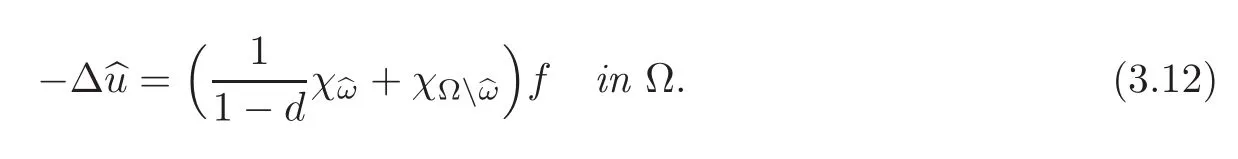
(2)

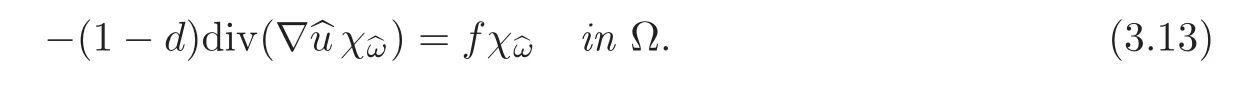
(3)

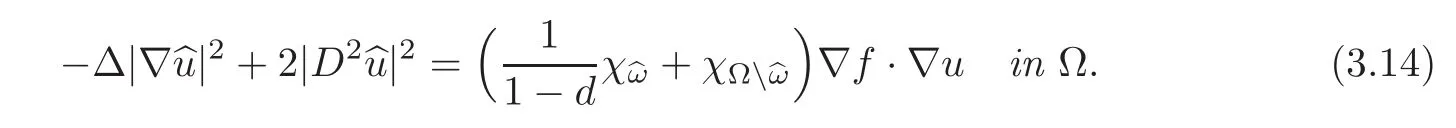
(4)If f does not change its sign anddefined by(3.6)does not vanish,then=χbωis the unique solution of(3.3).

(5)Assume f to be strictly positive or strictly negative,and consider an open set O⊂Ωand a neighborhood N of∂O.Then we have

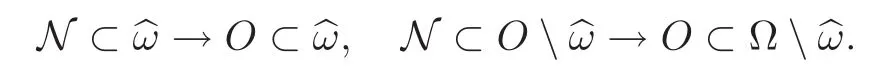
Remark 3.3(3.12)implies that iff ∈ Lp(Ω),thenCombined with(3.14)and the Sobolev imbedding theorem,this provides the existence of two derivatives forThis is related to the smoothness properties of the interfaces corresponding to the two materials α and β,which we recall,are contained in the sets

Equation(3.13)shows that the Neumann conditionon ∂ω is satisfied in a weak sense.

4 Applications to the Minimization of the First Eigenvalue

Another interesting problem in the optimal design of two-composites is the minimization of the first eigenvalue for the corresponding diffusion operator.Mathematically,it can be formulated as

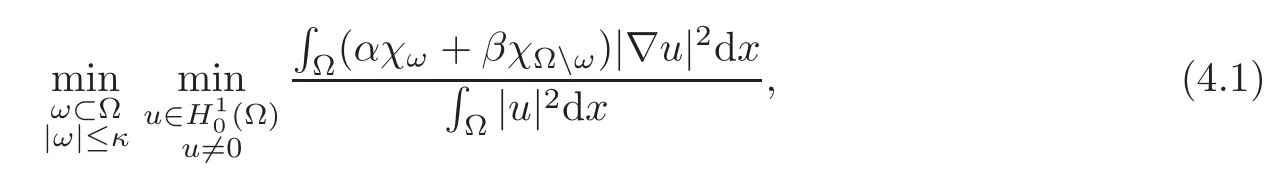
where,similar to the previous sections,we assume 0< α <β,0<κ<|Ω|.

Define c by(2.2),and the corresponding relaxed formulation is given by

A different formulation of(4.1)can be obtained by using the following result.

Lemma 4.1Assume A ∈ L∞(Ω)N×Nto be uniformly elliptic.Then the first eigenvalue of the operator−div(A∇u)with Dirichlet conditions

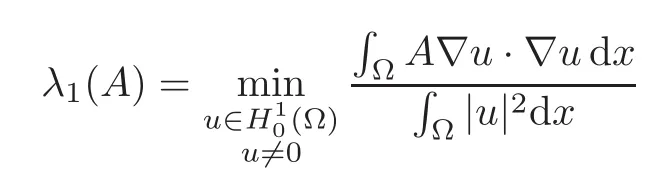
can be characterized by

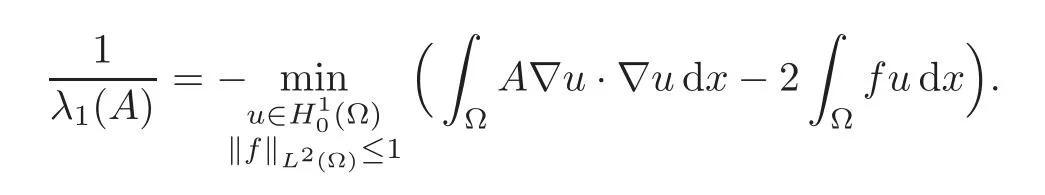
This lemma proves that(4.1)is equivalent to

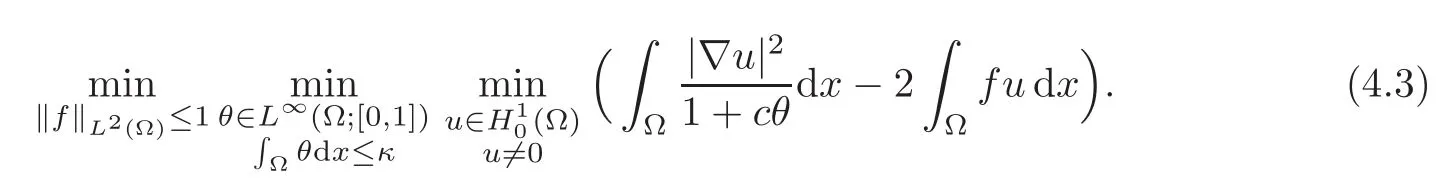
Therefore,comparing with(2.4),we see that the eigenvalue problem consists in solving the compliance problem(2.4)for every f ∈ L2(Ω)with a unitary norm,and then minimizing in f.Moreover,it is not difficult to check that iff is a function for which the maximum is attained,then f is an eigenfuction for the corresponding optimal mixture.From Theorem 2.4,we then have the following smoothness result.

Theorem 4.1Assume Ω∈C1,1.Then,ifis an optimal solution of(4.1),we have

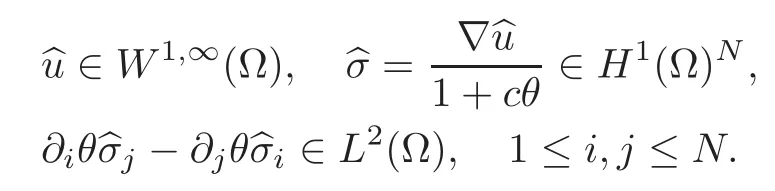
The results obtained in Theorem 2.5 can be used to obtain a counterexample to the existence of solution for the unrelaxed problem(4.1),that is,we have the following theorem.

Theorem 4.2AssumeThen for ε>0 small enough,the problem

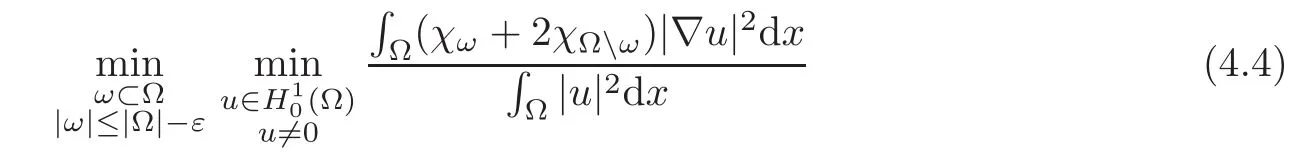
has not a solution.

Sketch of the ProofWe assume that there exists a solution ωε,uεof(4.4),with uε>0,kukL2(Ω)=1.Taking into account that|ωε|=|Ω|− ε,we get that uεis very close to the eigenfunction u corresponding to the first eigenvector of the Laplacian in Ω,which is given by

Now,the optimality conditions for(4.4)show that∂ωεis composed by level lines of uε.Then we deduce that there exists a component Oεof Ωωεwhich is close to the ellipse

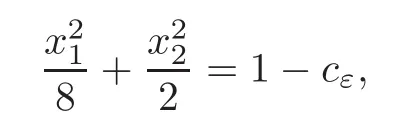
where cεtends to zero with ε.However,using our smoothness results for the solution of(4.4)(Ω is not smooth,but by Remark 2.1,we have local regularity)and Serrin’s theorem(see[17]),we must have that Oεis a ball.This contradiction shows the result.

Figures 1–3 below correspond to the numerical solution of problem

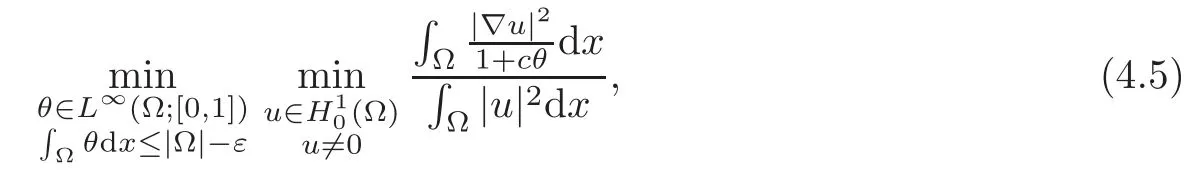
with Ω given by Theorem 4.2.This is the relaxed formulation of(4.4).The figures correspond to ε=0.5 ∼ 0.1|Ω|,ε=2 ∼ 0.4|Ω|and ε=3 ∼ 0.6|Ω|.In these pictures,the white zones correspond to the material α,the black zones to the material β and the grey figures to the homogenized materials.We observe that although in Theorem 4.2,we supposed that ε is small,grey zones appear in all the cases,and in fact,they are larger when ε is larger.

Figure 1 Optimal solution of(4.5)with ε=0.5.

Figure 2 Optimal solution of(4.5)with ε=2.

Figure 3 Optimal solution of(4.5)with ε=3.

[1]Allaire,G.,Shape Optimization by the Homogenization Method,Springer-Verlag,New York,2002.

[2]Briane,M.and Casado-Díaz,J.,Uniform convergence of sequences of solutions of two-dimensional linear elliptic equations with unbounded coefficients,J.Differential Equations,245,2008,2038–2054.

[3]Casado-Díaz,J.,Couce-Calvo,J.and Martín-Gómez,J.D.,Relaxation of a control problem in the coefficients with a functional of quadratic growth in the gradient,SIAM J.Control Optim.,43,2008,1428–1457.

[4]Casado-Díaz,J.,Smoothness properties for the optimal mixture of two isotropic materials,the compliance and eigenvalue problems,SIAM J.Control Optim.,to appear.

[5]Casado-Díaz,J.,Some smoothness results for the optimal design of a two-composite material which minimizes the energy,Calc.Var.PDE,53,2015,649–673.

[6]Chipot,M.and Evans,L.,Linearisation at infinity and Lipschitz estimates for certain problems in the calculus of variations,Proc.Roy.Soc.Edinburgh A,102,1986,291–303.

[7]Franchi,B.,Serapioni,R.and Serra Cassano,F.,Irregular solutions of linear degenerate elliptic equations,Potential Anal.,9,1998,201–216.

[8]Gilbarg,D.and Trudinger,N.S.,Elliptic Partial Differential Equations of Second Order,Springer-Verlag,Berlin,2001.

[9]Goodman,J.,Kohn,R.V.and Reyna,L.,Numerical study of a relaxed variational problem for optimal design,Comput.Methods Appl.Mech.Eng.,57,1986,107–127.

[10]Kawohl,B.,Stara,J.and Wittum,G.,Analysis and numerical studies of a problem of shape design,Arc.Rational Mech.Anal.,114,1991,343–363.

[11]Lions,J.L.,Some Methods in the Mathematical Analysis of Systems and Their Control,Science Press,Beijing,1981.

[12]Manfredi,J.J.,Weakly monotone functions,J.Geom.Anal.,4,1994,393–402.

[13]Murat,F.,Un contre-example pour le problème du contrôle dans les coefficients,C.R.A.S.Sci.Paris A,273,1971,708–711.

[14]Murat,F.,Théorèmes de non existence pour des problèmes de contrôle dans les coefficients,C.R.A.S.Sci.Paris A,274,1972,395–398.

[15]Murat,F.,H-Convergence,Sèminaire d’Analyse Fonctionnelle et Numèrique,Universitè d’Alger,1977–1978;English translation:H-Convergence,Topics in the Mathematical Modelling of Composite Materials,F.Murat and L.Tartar(eds.),Birkaüser,Boston,1998,21–43.

[16]Murat,F.and Tartar L.,Calcul des variations et homogénéisation,Les Méthodes de L’homogénéisation:Theorie et Applications en Physique,Eirolles,Paris,1985,319–369;English translation:Calculus of variations and homogenization,Topics in the Mathematical Modelling of Composite Materials,F.Murat and L.Tartar(eds.),Birkaüser,Boston,1998,139–174.

[17]Serrin J.,A symmetry problem in potential theory,Arch.Rat.Mech.Anal.,43,1971,304–318.

[18]Spagnolo,S.,Sulla convergenza di soluzioni di equazioni paraboliche ed ellittiche,Ann.Scuola Norm.Sup.Pisa Cl.Sci.,1968,571–597.

[19]Stampacchia,G.,Le probléme de Dirichlet pour leséquations elliptiques du second ordrecoefficients discontinus,Ann.Inst.Fourier Grenoble,15,1965,189–258.

[20]Tartar,L.,Estimations fines de coefficients Homogénéisés,Ennio de Giorgi Colloquium,Pitman,London,1985,168–187.

[21]Tartar,L.,Remarks on optimal design problems,Calculus of Variations,Homogenization and Continuum Mechanics,World Scientific,Singapore,1994,279–296.

[22]Tartar,L.,An introduction to the homogenization method in optimal design,Optimal Shape Design,Springer-Verlag,Berlin,2000,47–156.

[23]Tartar,L.,The general theory of the homogenization,A Personalized Introduction,Springer-Verlag,Berlin,2009.