A Penalty-Regularization-Operator Splitting Method for the Numerical Solution of a Scalar Eikonal Equation∗
Alexandre CABOUSSAT Roland GLOWINSKI
(In Honor of the Scientific Contributions of Professor Luc Tartar)
1 Introduction
Various mathematical models in science and engineering lead to the prototypical Eikonal equation|∇u|=1;this is the case particularly in optics,wave propagation,material science,differential geometry(geodesics)(see[32]),geophysics(see[37]),and image processing.The analysis of such nonlinear models can be found in[14](see also the references therein).Actually,the Eikonal equation is often associated with the Hamilton-Jacobi equation for wave propagation(as shown in[40]).
In this article,we are interested in the computation of the approximate solutions of the Dirichlet problem for a steady Eikonal equation.Namely,we want to findu:Ω⊂R2→R satisfying

wheregis a given data,and|·|is the canonical Euclidean norm.Problem(1.1)is a Dirichlet problem for the scalar Eikonal equation.Vector Eikonal equations,which are natural generalizations of(1.1),have been discussed in[15–17]for origami modeling.All these problems are examples of implicitly nonlinear equations(see[8,22]).
Numerical methods for the solution of this type of implicitly nonlinear equations can be found in,e.g.,[5,12–13,27].Related methods can be used for the solutions of the Hamilton-Jacobi equations and of some obstacle problems.Among these numerical methods,let us mention the fast marching methods(see[40]),the fast sweeping methods(see[42]),and the levelset-based methods(see[2]).Among the computational issues which have been and are currently investigated,let us mention the computational cost,the influence of the space discretization mesh,and the design of fast algorithms(see related references[30–31,37,41]).Similar problems,involving the infinity-Laplacian operator,arise in sand mechanics(see,e.g.,[1,3,35–36]).
Due to the low regularity and the possible multiplicity of the solutions of the scalar Eikonal equation,these solutions have to be defined in a generalized sense,the most commonly accepted one being the notion of viscosity solutions(see,e.g.,[11]).Other approaches are available as shown in,e.g.,[29].
Most methods for the numerical solution of the scalar Eikonal equation view it as a nonlinear hyperbolic problem.In this article,we take a different point of view,and attempt to solve(1.1)by using a calculus of variations approach relying on elliptic solvers and on the time-discretization by operator-splitting of an initial value problem associated with an Euler-Lagrange equation.Our approach,which is also well-suited to the solution of some Eikonal systems(see[12–13]),focuses on the computation of minimal and maximal solutions of(1.1),using a methodology combining:(i)A quadratic penalization of the Ginzburg-Landau type to relax the equation|∇u|=1,considered as a nonlinear equality constraint.(ii)A linear or nonlinear biharmonic regularization(see[3,21,28]).(iii)The use of an operator-splitting schemela Marchuk-Yanenko to time-discretize an initial value problem associated with the Euler-Lagrange equation of the above regularized problem.(iv)A low-orderC0-conforming fi nite element approximation,well-suited to the Lipschitz continuous regularity of the solutions and to domains with a curved boundary.
The operator-splitting approach allows the decoupling of the differential operators from the Ginzburg-Landau nonlinearity.Actually,these techniques have been successfully applied by the authors to other situations,such as Monge-Ampre and Pucci equations(see[6,9,18–19,26]),visco-plastic or particulate flow(see[20,24])and other problems involving non-smooth operators(see[3–4,33]).
The article is organized as follows:In Section 2,we formulate particular cases of(1.1),leading to minimal and maximal solutions.Equivalent and regularized formulations are given in Section 3.Our computational approach is described in Section 4,while in Section 5 we briefly describe another regularization approach.The finite element implementation of our methodology is discussed in Section 6 with the corresponding numerical results being presented in Section 7.Finally,among other comments,a viscosity interpretation of our methodology will be given in Section 8.
2 Problem Formulation
Let Ω be a bounded domain of R2;we suppose that the boundary Γ :=∂Ω is at least Lipschitz continuous in the sense of Neas[34].The steady scalar Eikonal equation we want to solve reads as follows:Findu:Ω→R verifying

We observe that,up to the addition of a constant,we can always suppose thatg≥0.Since problem(2.1)has infinitely many solutions,in general,it makes sense to enforce uniqueness by imposing additional conditions.In this article,we will impose on the solution to be maximal in the sense ofL1(Ω)(actually,we can also impose on the solution to be minimal).
Remark 2.1If the equation|∇u|=1 is replaced by the more general situation|∇u|=f(≥0),the numerical approach presented in this work also applies with straightforward modifi cations.
In order to obtain the maximal solution,we actually requireuto maximize the linear functional

over

instead of maximizing theL1-norm overEg.This change of the cost function is easy to justify:Indeed suppose thatumaximizes the functional(2.2)overEg.Sinceg≥0 and|∇|u||=|∇u|,we also have|u|∈Eg.By the definition ofu,we have

On the other hand,the relationu≤|u|implies that

It follows that

The non-negativity of the integrand|u|−u≥0 implies thatu=|u|,that is,the non-negativity ofu.Actually,we can easily prove that the above function is also the upper hull of all the functions inEg,that is,the(necessarily unique(see[38]))functionuofEgverifying
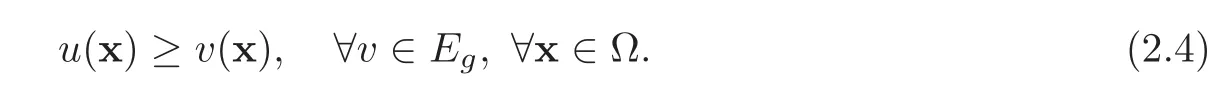
Remark 2.2In order to find the smallest solution of(2.1)in the sense of(2.4),that is,

we would minimize overEgthe functional
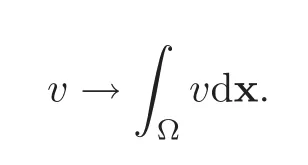
Remark 2.3Ifg=0,the maximizer of(2.2)is nothing but the distance function to the boundary of the domainx→δ(x,Γ).For example,in one dimension of space,if Ω =(0,1),thenu(x)=min(x,1−x);in two dimensions of space,if Ω =(0,1)×(0,1),then
u(x)=u(x1,x2)=min(x1,x2,1−x1,1−x2),∀x={x1,x2}∈Ω.
If Ω is the disk of radiusRcentered at 0,then
In the remainder of this article,we describe a numerical method for the approximate computation of the maximal and minimal solutions in the general case.
3 Modeling,Regularization and Penalization
LetC>0 be a given positive constant.We first note that there is an equivalence between

and
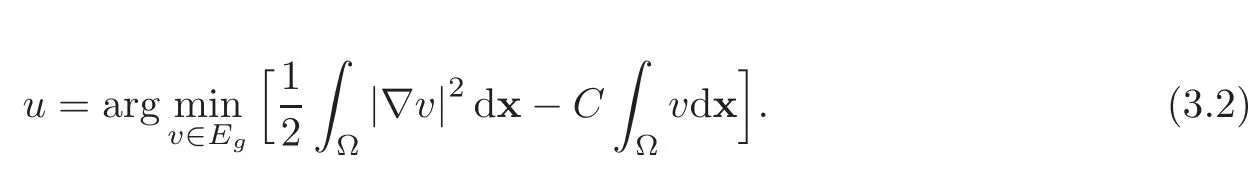
The main difficulty with(3.2)is the nonlinear constraint|∇v|=1(which is equivalent to|∇v|2=1).To handle this constraint we are going to use a penalization approach preserving the differentiability of the cost functional.Letε>0 be a small parameter;we thus approximate(3.2)by

where

Based on past experience with related problems(see,e.g.,[6,12–13]),we introduce a biharmonic regularization.We thus consider a positive constantη>0 and a regularized variant of(3.3)that reads:
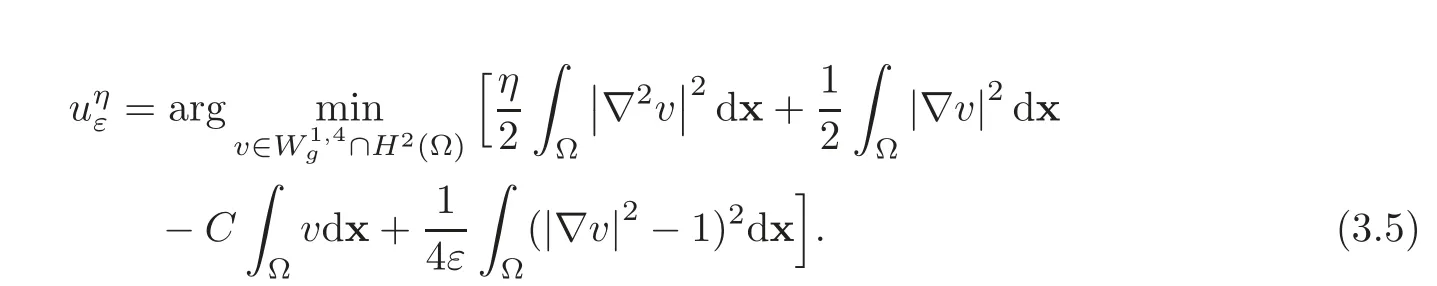
The introduction of the regularization termdxcorresponds to adding the biharmonic term−η∇2uto the first-order optimality conditions,together with the natural boundary condition∇2u=0 on Γ.
Remark 3.1(A Nonlinear Biharmonic Regularization) Another regularized variant of(3.3)that is inspired from image-processing techniques(see[10])reads as follows:

In the following sections,we are going to discuss mainly the iterative solution of problem(3.5).Due to the interesting features of problem(3.6),we will discuss it briefly aside in Section 5.
Remark 3.2In order to capture the minimal solution instead of the maximal solution,it suffices to changeCin−Cin(3.2)(and in(3.5)–(3.6)),Cstill being a strictly positive constant.
Remark 3.3For the sake of rigor,we should replace in(3.5),gby a regularized versionsuch thatActually,the numerical results reported in Section 7 show that using Lipschitz continuous functionsgwithout the(Γ)-regularity has no computational incidence in practice.
4 On the Solution of the Regularized Variational Problem
4.1 Mixed formulation and optimality conditions
After dropping the indicesεandη,(3.5)reads as follows:

In order to solve(4.1),let us define the functionu1as the unique solution of the following linear variational problem:Findsatisfying

The functionu1is the solution of the Poisson-Dirichlet problem:−∇2u1= 1 in Ω,with boundary conditionsu=gon Γ.If Γ is smooth and/or Ω convex,the functionu1has enough regularity to belong toSinceit follows from(4.2)that

Relationship(4.3)implies thatwhich implies in turn that(4.1)is equivalent to
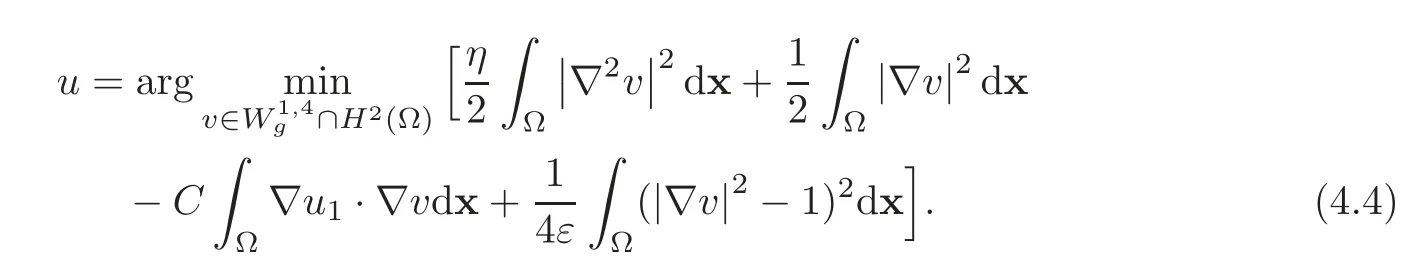
The rationale behind the introduction ofu1and the alternative formulation(4.4)is to have∇u,instead ofu,as the master unknown,the new problem having better decomposition properties.We denote by p the vector-valued function∇u,and define the vector space Q by
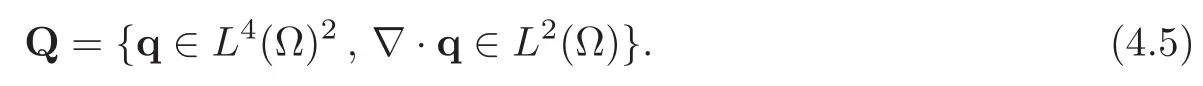
Setting q:=∇v,there is equivalence between(4.4)and the following non-convex nonlinear variational problem(of the mixed type):
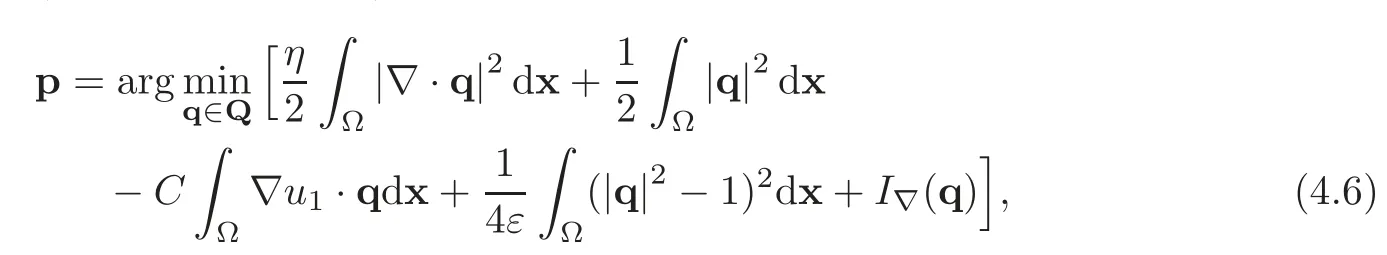
whereI∇(·)is the indicator functional of the spacethat is,
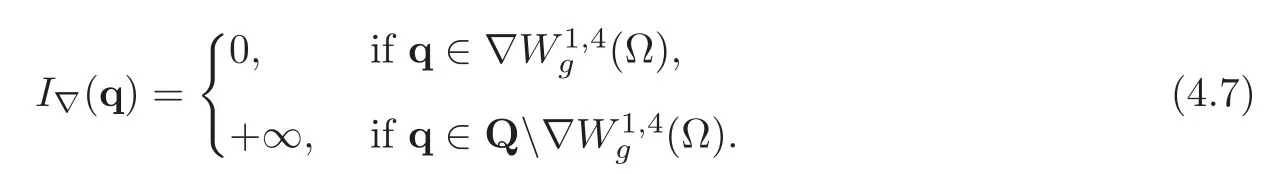
We observe that in(4.6),the quartic term is of the Ginzburg-Landau type.In the variational form,the Euler-Lagrange equation associated with(4.6)reads as follows:Find p∈Q satisfying
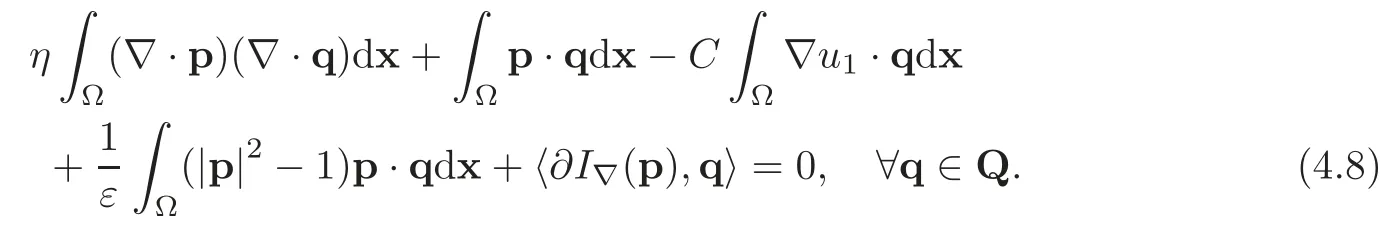
Here∂I∇(p)denotes the subgradient of the functionalI∇(·)evaluated at p(see[38]).
Remark 4.1Instead of definingu1as the solution of−∇2u1=1 in Ω,together withu1=gon Γ,we could have defined it as the solution of−∇2u1=1 in Ω,together withu1=0 on Γ.
4.2 Initial-value problem and operator-splitting
We associate with(4.8)the following initial-value problem(flow in the dynamical system terminology):Find p(t)∈Q for a.e.t∈(0,+∞)satisfying

Our aim is to find a stationary solution to the initial-value problem(IVP for short)(4.9).In order to solve this IVP,we advocate an operator-splitting schemela Marchuk-Yanenko(see,e.g.,[24,Chapter 6])for its robustness and simplicity.Note that other schemes are available(like the Strang symmetrized one).Let us denote byτ>0 a time-discretization step and settn=nτ,n=0,1,2,···.Let pnbe an approximation of p(tn).In order to solve(4.9),we advocate the following operator-splitting scheme:Initialize with

Forn≥0,pnbeing known,we computesuccessively via the solution of:

Actually,problem(4.11)can be solved point-wise,corresponding thus to an infinite family of low-dimensional optimization problems.On the other hand,(4.12)is a classical linear variational problem written in a mixed form.We are going to discuss in the following sections the solution of these two problems.The initialization of algorithm(4.10)–(4.12)is the topic of the next remark.
Remark 4.2(Initialization of the IVP)Choosing sensibly p0in(4.10)is an important issue in order to reduce the number of time steps necessary to achieve convergence.We thus advocate the following approach:Solve−∇2u0=C/|C|in Ω,withu0=gon Γ.Then,we define p0by
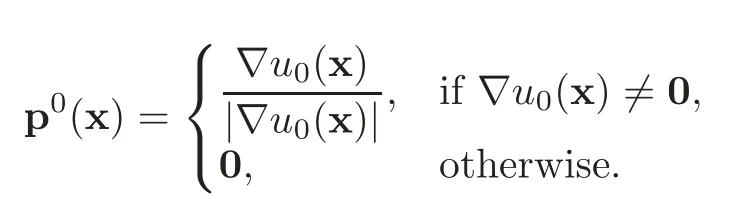
4.3 Solution of the local optimization problems
Problem(4.11)does not involve any derivatives.Thus it can be solved locally for almost every point x∈Ω.Rewriting(4.11)locally,we see thatverifies
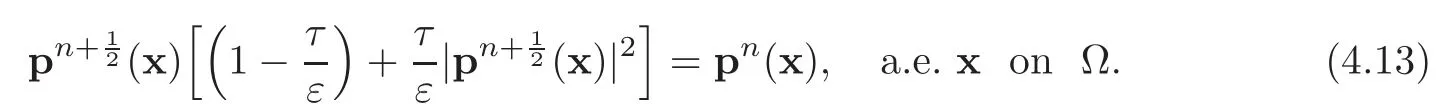
Taking the canonical Euclidean norm of both sides of the vector-valued equation(4.13),it follows thatis a solution of the real-valued cubic equation:

If the conditionτ≤εholds,the equation(4.14)has a unique solution,necessarily non-negative.Onceis known,we obtainfrom(4.13)by setting

To solve the nonlinear equation(4.14),we advocate the Newton-Raphson method starting from the initial guessz0=1;the consecutive iterates are thus,fork≥0,

In practice,after an appropriate finite difference or finite element approximation,we have to solve at each time step a cubic equation such as(4.14)for each point(resp.triangle)of the associated finite difference(resp.finite element)grid.Since Ω is bounded in R2,the number of such cubic equations is of the order ofh−2,wherehis a space-discretization step.
4.4 Solution of the linear variational problems
Problem(4.12)is simpler to solve than it looks like.Indeed,setting
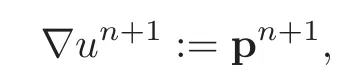
problem(4.12)is equivalent to findingthat satisfy
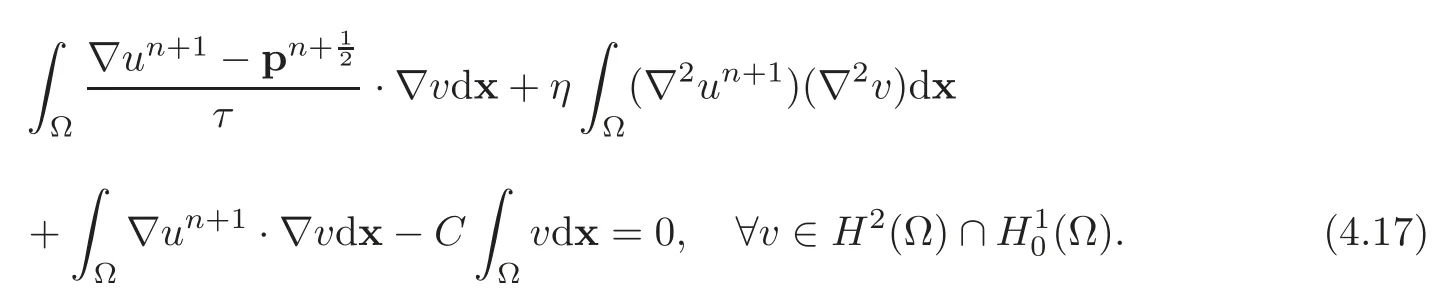
Problem(4.17)is nothing but a variational formulation of the following biharmonic problem:

Such a biharmonic problem is equivalent to the following system of two well-posed second-order linear elliptic problems:
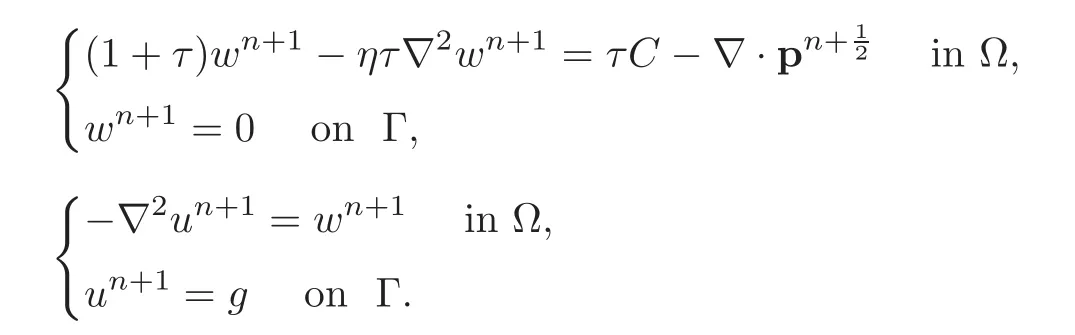
Anticipating Section 6,boundary-layer considerations suggest takingwithhbeing a space-discretization step.Many direct and iterative methods are available for the numerical solution of the above two elliptic boundary value problems(in fact,of their discrete analogues;see,e.g.,[24]and the references therein).In order to speed up the convergence,we can use the following strategy to varyεandτat each step of the operator-splitting scheme:
(a)As long astake

withξ∈(0,1).
(b)Ifητn≤χh2,take

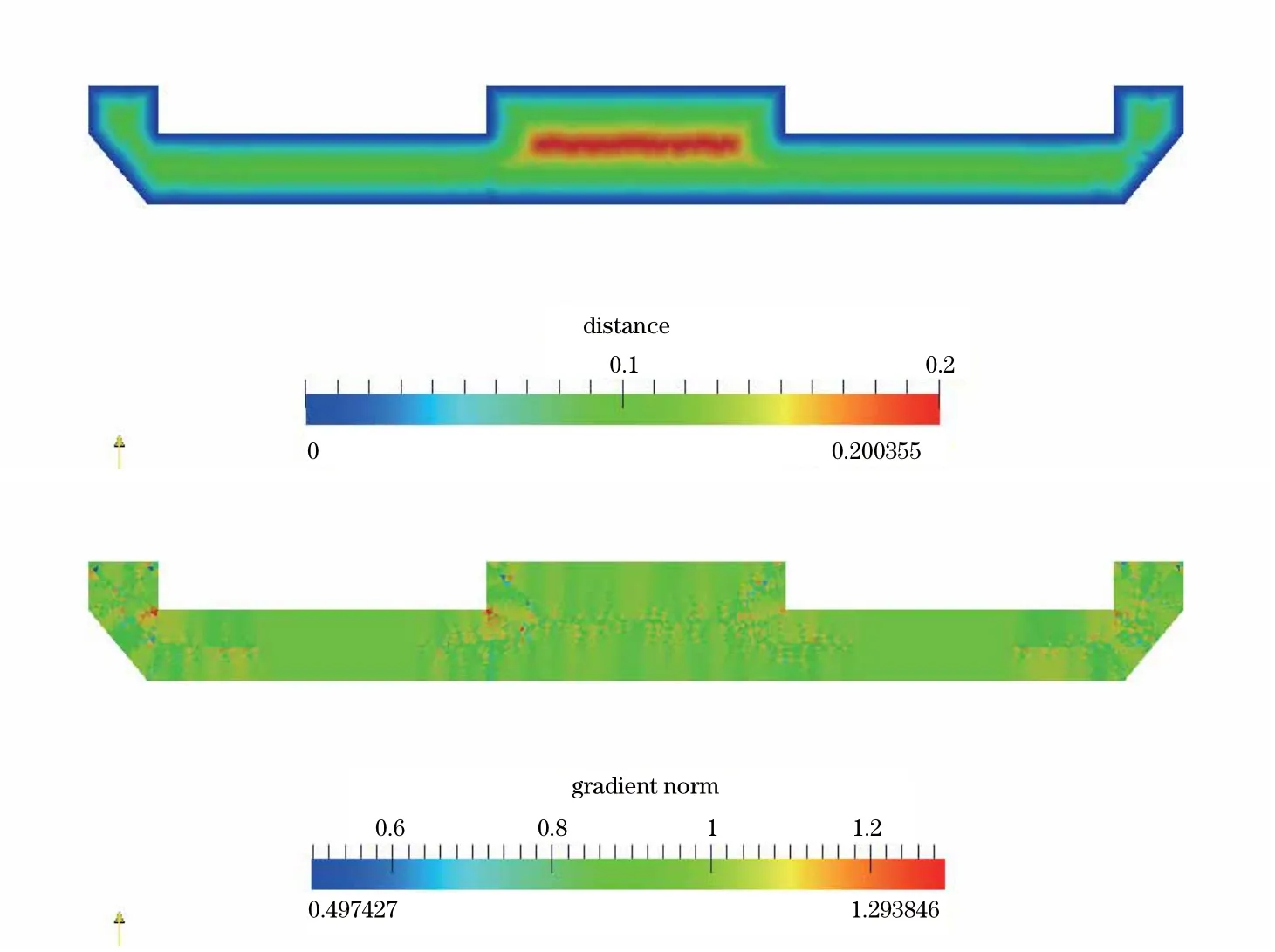
Relationship(4.19)is motivated by the fact that ifτngoes to zero too rapidly,the time integration never reachest=+∞,and thus the steady state cannot be reached in the most stringent cases.Similarly,ifητn< The influence of the choice of the constantCis not crucial.An appropriate choice forCleads to the most appropriate topology of the objective function,and may improve the global convergence of the algorithm. After dropping the indicesεandη,(3.6)reads as follows: Ifu1is still defined by(4.2),and if p=∇u,then(5.1)is equivalent to where In the variational form,the Euler-Lagrange equation associated with(5.2)reads as follows:Findsatisfying with∂I∇(·)the sub-gradient of the functionalI∇at p.As in Section 4,we associate with(5.3)an initial-value problem similar to(4.9),namely,to findfor a.e.t∈(0,+∞)satisfying p(0)=p0and Following the approach we took in Section 4,we are going to use again an operator-splitting schemela Marchuk-Yanenko to solve the problem(5.4).The initialization and the solution to the local optimization problems are similar to those in Section 4.The main difference has to do with the solution of the variational problem(4.12),which now reads:Findsatisfying By setting∇un+1:=pn+1,there is equivalence between the problem(5.5)and findingun+1∈that satisfy The problem(5.6)is nothing but the variational formulation of the following nonlinear biharmonic problem: which is equivalent to the following system of second-order elliptic equations: The first of these second-order elliptic equations can be formulated in the divergence form,namely, From the small size of the coefficientητ,it is tempting to use,in practice,the following simple linearization: The elliptic operator in(5.8)is linear,self-adjoint and strictly positive.Using(5.8)avoids solving the nonlinear problem(5.7)by Newton’s,quasi-Newton,or other methods. Remark 5.1If for some reason,w0is required(as it will be if we use(5.8)instead of(5.7)),we can takew0=C. Finite element methods are well-suited to the solution of variational problems such as(3.5)(or(3.6)),particularly those methods relying on continuous piecewise linear approximations on triangulations of Ω.Indeed,piecewise linear finite element methods rely on spaces of Lipschitz continuous functions well-suited to the approximation of solutions to the Eikonal equation,whose regularity is precisely Lipschitz,and whose second derivatives do not have,in general,anLs(Ω)-regularity,even fors=1,implying that higher-order methods will not bring additional accuracy. Let us define a space discretization steph>0,and associate withha triangulationThthat satisfies the usual compatibility conditions(see,e.g.,[25]for a complete definition).Let us denote by Σhthe(finite)set of the vertices ofTh,byNhthe number of elements in Σh,and by Σ0hthe subset of those elements in Σhnot located on Γ (withN0h:=card(Σ0h)).From the triangulationTh,we define the following finite element spaces: where P1is the space of the two-variable polynomials of degree≤1.We clearly have With each pointPi∈Σh,we associate the piecewise linear basis functionϕi∈Vh,i=1,···,Nh,uniquely defined byϕi(Pi)=1,ϕi(Pj)=0,j=1,···,Nh,j≠i.Next,we equipVh,and its sub-spacesV0handVghwith the following discrete scalar product: and the corresponding normfor allv∈Vh;above,Akdenotes the area of the polygonal domain which is the union of those triangles ofThwhich havePkas a common vertex.In a similar fashion,we equip the space Qhwith the scalar product and the norm respectively defined as follows: and(with|K|=area ofK). After dropping the indicesεandη,we approximate the problem(3.5)by whereθ=θ(v)∈V0his defined fromvvia the solution of the following finite-dimensional linear variational problem: The optimality conditions associated with(6.2)–(6.3)read as follows:Find{uh,wh}∈Vgh×V0hsuch that The main difficulty with problem(6.4)is its cubic nonlinearity.In order to decouple this nonlinearity from the differential operators,we observe that(6.4)is equivalent to the following system: whereθ=θ(q)is obtained from q as the unique solution of the discrete linear variational problem: In(6.6),the functionu1is the unique solution of the discrete variational problem and the functionalI∇(·)(an indicator functional)is defined by The optimality conditions associated with this extended system(6.6)–(6.7)read as follows:Find{p,w,θ}∈Qh×V0h×V0hsuch that: for all{q,v}∈Qh×V0h. As in Subsection 4.2,we associate with(6.10)–(6.12)an initial-value problem that corresponds to a finite-dimensional flow in the dynamical system sense.The variational formulation of this initial-value problem reads as follows:Find{p(t),w(t)}∈Qh×V0h,for a.e.t∈(0,∞),satisfying for all q∈Qh,together withθ∈V0h, and the initial condition p(0)=p0given in Qh.For the choice of p0,we suggest to compute first the solution of the discrete Poisson problem:Findu0∈Vghsuch thatfor allv∈V0hand then set Letτ(>0)be the time-discretization step.To time-discretize the initial-value problem(6.13)–(6.14),we advocate the following Marchuk-Yanenko-type scheme:Starting with p0=p0,we compute pn+1from pn,forn≥0,via the following time-splitting scheme: 1.Solve the discrete nonlinear problem:Findsuch that for all q∈Qh. 2.Solve the discrete variational problem:Find{pn+1,wn+1}∈Qh×V0hsuch that together with Remark 6.1Let us introduce pn+1=∇un+1;there is then equivalence between system(6.17)–(6.18)and findingthat satisfy both for allv∈V0h. The finite-dimensional nonlinear problem(6.16)can be solved triangle-wise;indeed,if we denote q|Kby qK,we can rewrite(6.16)as follows:Findsatisfying Let us assume from now on thatε≥τ;under this assumption,we observe thatis the unique solution of the cubic one-variable equation: The Newton’s method can be applied to the solution of(6.20).Once theare known,we obtainfrom The discrete linear variational problem(6.17)–(6.18)is of the mixed type;it consists of two discrete elliptic problems,each of them being equivalent to a linear system associated with a matrix which is sparse,symmetric and positive definite.A large variety of solution methods exists for such systems,while among them are the fast elliptic solvers of FISHPACK if the mesh is uniform,and the sparse Cholesky solvers,like those available in MATLAB.Clearly,the approximation methods discussed in Subsections 6.1–6.4 can be easily modified in order to handle the numerical solution of the nonlinearly regularized problem(5.1)via the operatorsplitting scheme(5.5)–(5.6). In this section,we will present the results of numerical experiments.Most of them are concerned(not surprisingly)with the particular case where Ω=(0,1)2,however,test problems where Ω has a(totally or partially)curved boundary or where Ω is not convex will also be considered.The finite element triangulations we use are either structured or isotropicla Delaunay.All the experiments have been performed on an Intel Xeon computer(2.93 GHz)with 8 GB memory.The results have been post-processed with Paraview. Let us consider Ω=(0,1)2.The first numerical example corresponds to the homogeneous caseg=0 in(2.1).The maximal solution to(2.1)is clearly the distance function x→δ(x,Γ)(distance of x to the boundary Γ of Ω);it is given here by Figure 1 Distance function on the unit square(g=0).Approximation uhof the solution of the Eikonal equation(h=,after 100 iterations).Left:Maximal solution;right:Minimal solution.First row:Graph of uh,second row:Contours of uh,third row:Piecewise constant approximation of|∇uh|. Sinceg=0,the minimal solution of(2.1)is just the opposite of the maximal one,i.e.umin=−umax.For our computations,we have used the strategy with variableεandτas described in(4.18)and(4.19),withε0=0.1,τ0=0.09,ξ=0.9,and the other parameters beingη=0.1 andC=10.The finite element mesh we use is a structured triangulationThof the “British flag”type wherehdenotes the length of the edges adjacent to the right angles.For the solution of the local nonlinear 2×2 systems,we have used the Newton’s method with the stopping criterion tolerance equal to 10−4;with this tolerance,the Newton’s algorithm was always converging in less than 10 iterations,typically. In Figure 1,we have reported,using linear biharmonic regularization,the graph of the computed maximal and minimal solutions,their contours,and the “contours”of|∇umax,h|and|∇umin,h|obtained withand 100 iterations(in fact,100-time steps of the operatorsplitting scheme(6.16)–(6.18)).Numerically,we also obtainumin,h=−umax,h.As an indication,the maximal value forumax,his 0.500164 for0.500211 forand 0.500228 forwhich are accurate approximations of the maximal value ofumax,which is 0.5.These results show that the Eikonal equation is satisfied,up to rounding errors and mesh effects(indeed,0.999662 ≤ |∇umax,h|=|∇umin,h|≤ 1.000546,a.e.on Ω if Figure 2 Computed distance function on the unit square(g=0;linear biharmonic regularization).Approximation errors||uh−umin||0hand||∇(uh−umin)||(resp.||uh−umax||0hand||∇(uh−umax)||)versus h(100 outer iterations).Left:Maximal solution;right:Minimal solution. Figure 3 Computed distance function on the unit square(g=0;nonlinear biharmonic regularization).Approximation errors||uh−umin||0hand||∇(uh−umin)||(resp.||uh−umax||0hand||∇(uh−umax)||)versus h(100 outer iterations).Left:Maximal solution;right:Minimal solution. Convergence results are visualized in Figure 2;they show theapproximation error for both theL2andH1-norms,wheneveru=umaxoru=umin.The low regularity of the solution(they belong toexplains why we do not obtain the usualO(h2)andO(h)approximation errors. If we use the nonlinear biharmonic regularization discussed in Section 5,we obtain numerical results very close to those obtained with the linear regularization from Sections 3–4.The related convergence results are shown in Figure 3:they are close to those obtained with the linear regularization and thus the difference does not warrant further comparisons. Remark 7.1The various numerical experiments we have performed in this article show that if they can be employed(which is definitely the case with square domains),“British flag”-type meshes behave quite well compared with other types of triangulations.This is in strong contrast with what we observed when solving,also via a nonlinear biharmonic approach,the elliptic Monge-Ampère equation detD2u=f(withf>0,D2ubeing the Hessian ofu);indeed for this fully nonlinear elliptic equation,the worst numerical results were obtained with“British flag”triangulations(see[6]for details). There is nothing mysterious about these different behaviors:Indeed,for the Eikonal equation discussed here,the biharmonic terms∇4uandhave been introduced for smoothing purposes,being multiplied by a small coefficient(of the order ofh2for their discrete analogues);on the other hand,when solving the above Monge-Ampre equation,the discrete second-order derivatives associated with “British flag” triangulations are very poor approximations of their continuous counterparts,explaining the bad results they produce. Ifg=0,the maximal solution to(2.1)is the distance to the boundary function,whatever the(convex)domain Ω is(see,e.g.,[12]).We consider here the following two-dimensional domains,namely,the unit disk,an ellipse of axes of length 1 and 2,and the half-disk.The values of the numerical parameters are the same as in Subsection 7.1,exceptCthat we take equal to 500 here.In Figure 4(the top row),we have reported the graph of the computed approximationsuhof the distance function for the three domains above using the linear biharmonic regularization.There is no doubt that using piecewise linear approximations greatly facilitates the solution of the Eikonal equation(2.1)on domains with curved boundary(see also[6]).In Figure 4(the bottom row),we have visualized|∇uh|:The relation|∇uh|=1 is accurately verified,the discrepancies being very localized(along edges and at corners,in particular);this behavior was expected,but overall the numerical results we obtained show the robustness of our approach.In Figure 5,in the particular case of the unit disk,we have visualized the convergence properties of the computed approximate solutions obtained by using both the linear and nonlinear biharmonic regularizations:Both regularizations produce essentially the same results,suggestingO(h12)for both||uh−u||0hand||∇(uh−u)||. Figure 4 Computed distance function on domains Ω with curved boundaries(g=0,linear biharmonic regularization).Approximation uhof the solution of the Eikonal equation(h=,after 100 iterations).Top:Graphs of the computed maximal solutions uh.Bottom:Visualization of|∇uh|. Actually,for the(upper)half-disk domain,the exact maximal solution is given by Figure 5 Computed distance function of the unit disk(g=0,linear and nonlinear biharmonic regularizations).Approximation errors||uh−umax||0hand||∇(uh−umax)||versus h.Number of iterations:100. the ridge being the curvilinear arc whose equation,in polar coordinates,is given by withθ∈[0,].This function takes a maximal value ofat the pointFigure 6(left)visualizes the order of convergence of theL2-norm of the approximation error,while Figure 6(right)visualizes the error on the maximum value,that is||uh|∞−0.5|.Both display an approximation error of orderh2,suggesting some kind of super-convergence in this particular case. Figure 6 Computed distance function of the half-disk(g=0).Approximation errors||uh−umax||0h(left)and||uh|−0.5|(right)versus h.Number of iterations:200. The numerical example we consider now concerns the search of the maximal and minimal solutions of the Eikonal equation(2.1)when Ω=(0,1)2andgis defined by where Γ1=[0,1]×{0},Γ2={1}×(0,1),Γ3=[0,1]×{1}and Γ4={0}×(0,1).The corresponding maximal solution is given by On the other hand,the closed form of the minimal solution is given by In order to solve numerically this new test problem,we have taken(i)ε0=0.25,τ0=0.2,η=10−3,C=10 andand(ii)ε0=0.25,τ0=0.2,η=10−3,C=100 andThe mesh used is a structured mesh where the square cells are split into two triangles according to the first diagonal.When calculating the minimal solutions,parameters are identical except thatC=−100.Figures 7–8 visualize the maximal and minimal solutions respectively.For instance,the maximal solution reaches a maximal value of 0.503278 instead of the theoretical value of 0.5 Figure 7 Non-homogeneous boundary conditions on the unit square(I).Approximation uhof the maximal solution of the Eikonal equationh=,after 500 iterations.Top left:Graph of uh;top right:Graph of u;bottom left:Contour of|uh|;bottom right:Visualization of|∇uh|. Looking at the gradient|∇uh|,one can observe that it is almost everywhere equal to one.The exception is in the neighborhood of an edge,due to the mesh effects.Note that for the maximal solution for instance,the approximation error due to the mesh is only present when mesh edges are perpendicular to the solution’s ridges. Figure 8 Non-homogeneous boundary conditions on the unit square(I).Approximation uhof the minimal solution of the Eikonal equationh=,after 700 iterations.Top left:Graph of uh;top right:Graph of u;bottom left:Contour of|uh|;bottom right:Visualization of|∇uh|. Figure 9 Non-homogeneous boundary conditions on the unit square(I)(linear biharmonic regularization).Approximation uhof the solution of the Eikonal equation.Left:Maximal solution,cut along Ox1at x2=;middle:Minimal solution,cut along Ox1 at x2=;right:Minimal solution,cut along Ox2at x1=h=–black– exact solution –red–,after 500 iterations. Figure 9 shows cuts of the graph of the maximal and minimal solutions for the approximation solution and the exact solution(interpolated on the same mesh).The cut of the maximal solution(left)shows that as expected,the discrepancy between the exact and computed maximal solutions is maximal at,the point where the three lines of discontinuity of∇umaxencounter. Figure 10 Non-homogeneous boundary conditions on the unit square(I)(linear biharmonic regularization).Approximation errors||uh−umin||0h(resp.||uh−umax||0h)versus h for various types of discretizations(“British-flag” mesh and unstructured mesh).Left:Maximal solution;right:Minimal solution. The cuts of the minimal solution show that along theOx1direction,the approximation is close to the exact solution with a little diffusion effect.Along theOx2direction,one sees that the approximation is more diffusive. Figure 10 visualizes the convergence properties of the computed approximate solutions obtained on various types of discretizations of the unit square using the linear biharmonic regularization.We consider the “British flag” discretization,and a Delaunay discretization(“unstructured mesh”).All types of meshes produce essentially the same results,suggestingfor||uh−u||0h.When the edges of the mesh follows the lines of discontinuity of the gradient of the solution,the convergence order is actually closer fromO(h),suggesting some kind of super convergence,a property that was expected. This numerical example corresponds to the following boundary conditions: where Γ1=[0,1]×{0},Γ2={1}×(0,1),Γ3=[0,1]×{1}and Γ4={0}×(0,1).The maximal and minimal solutions are respectively given by: and Note that these solutions of the closed form are identified after looking at the numerical results obtained by our method,showing once again that numerical investigations can be useful in order to determine exact solutions.They are consistent with the results of Caffarelli and Crandall[7]who show that,away from the singularities of∇u,the solutions of the Eikonal equation|∇u|=1 are piecewise affine or conical.Numerical parameters are the same as those used for the test case with non-homogeneous boundary conditions(I).Figures 11 and 12 visualize the maximal and minimal solutions respectively,for two different(coarse and fine)mesh discretizations.This test case is the most stringent one in terms of convergence behavior.Figure 13 illustrates cuts of the graph of the minimal or maximal solutions for the approximation solution and the exact solution(interpolated on the same mesh).These cuts show that the solution is well approximated,except for mesh effects(for instance,along the diagonal line where the ridge is perpendicular to the mesh edges). Studyingumax,we observe that the maximal value is reached at(0.5,0.5)with a value ofwhich is close to the values obtained by the numerical approximations.Concerningumin,its minimal value is zero and is also obtained at(0.5,0.5);here again the numerical approximation agrees with the exact solution. Figure 14 visualizes the convergence properties of the computed approximate solutions obtained for the various types of discretizations of the unit square using the linear biharmonic regularization.These results suggest a convergence order for the error||uh−u||0hthat is betweenandO(h).Here,the “British flag” mesh allows to track more accurately the edges of the solution(i.e.,the lines of discontinuity of the gradient of the solution)than the asymmetric mesh that is oriented along one diagonal.The more general,unstructured mesh actually performs also better than the asymmetric mesh in that regard.A clear mesh effect is thus observed for the convergence orders. Remark 7.2When(2.1)is replaced by as in[5,12]for instance,the minimal and maximal solutions can be described analytically in a relatively simple fashion: umax(x1,x2)=min(x1,1−x1)+min(x2,1−x2) Figure 11 Non-homogeneous boundary conditions on the unit square(II);minimal solution.Approximation uhof the solution of the Eikonal equation(after 100 iterations).Left:h=;right:h=.First row:Graph of uh;second row:Contours of the graph;third row:Piecewise constant approximation∇uh. and This stresses out clearly some obvious difference between the solution of(2.1)and that of(7.8),for the same domain and boundary data. Figure 12 Non-homogeneous boundary conditions on the unit square(II);maximal solution.Approximation uhof the solution of the Eikonal equation(after 100 iterations).Left:h=;right:h=.First row:Graph of uh;second row:Contours of the graph;third row:Piecewise constant approximation∇uh. This numerical example corresponds to the following boundary conditions: where Γ1=[0,1]×{0}, Γ2={1}×(0,1), Γ3=[0,1]×{1}and Γ4={0}×(0,1),andis a constant less than.The maximal and minimal solutions are not analytically known,and the boundary conditions do not satisfy the assumptions in[7].In particular,the functionnot being piecewise affine or parabolic,it cannot be the trace of a solution of the Eikonal equation(2.1).Figure 15 visualizes the maximal and minimal solutions,as well as their contours and the corresponding gradients.One can observe that except in a boundary layer in a neighborhood of Γ2,in particular,around the corners of Ω,the solution is a union of cones and affine functions.The imposition of these boundary conditions do not jeopardize the global convergence properties of the algorithm. Figure 14 Non-homogeneous boundary conditions on the unit square(II)(linear biharmonic regularization).Approximation errors||uh−umin||0h(resp.||uh−umax||0h)versus h for various types of discretizations(asymmetric structured mesh,“British-flag”mesh,and unstructured mesh).Left:Maximal solution;right:Minimal solution. Figure 15 Non-homogeneous boundary conditions on the unit square(III).Approximation uhof the solution of the Eikonal equation(after 500 iterations).First row:Graph of uh;second row:Contours of|uh|;third row:Visualization of|∇uh|.Left:Maximal solution;right:Minimal solution. Finally,let us qualitatively describe the use of the Eikonal equation for an application in computational fluid dynamics.When modeling turbulence in computational fluid dynamics,several models involve a mixing length(see[39]).Namely,the local turbulent viscosity is a function of the distance between the given point and the boundary of the computational domain.The proposed algorithm can be used to easily compute the distance to the boundary for any arbitrary domain Ω. As an illustration,let us consider a two dimensional cut of an aluminum Hall-Héroult cell(see,e.g.,[23]for details).Dimensions are approximately 3[m]×0.4[m].In applications,a magneto-hydrodynamic problem has to be solved in such a domain;the computation of velocity and pressure fields via the solution of the Navier-Stokes equations usually involves turbulence effects. Figure 16 CFD application.Distance to the boundary for industrial application.Top:Contours of the approximation uhof the solution of the Eikonal equation.Bottom:Piecewise constant approximation|∇uh|. Figure 16 visualizes the approximation of the distance obtained with our algorithm for this particular geometry.The boundary data isg(x1,x2)=0 for all(x1,x2)∈∂Ω,so that the solution is the distance to the boundary.The mesh contains approx.3300 nodes and 6600 elements.Typical CPU time is around 20[s]per outer iteration and a satisfactory stationary solution can be obtained after approx.10 iterations.The gradient norm is equal to one almost everywhere,except in the corners of the domain(especially the entrant corners where the domain is not convex). Let us briefly describe the viscosity solution interpretation of the approximated solutions obtained with this penalty-regularization-operator splitting method.Despite the fact that the proposed algorithm is variational in nature,and relies on elliptic solvers,one can write it as the solution to some viscosity equation. Let us suppose that Ω is simply connected,and defineandandWe can easily show that(4.8)can be rewritten as together with appropriate boundary conditions.Problem(8.1)is a kind of Ginzburg-Landau nonlinear Stokes problem.It emphasizes thatuis linked to the solution v of a(kind of)viscous fluid flow equation. A numerical method for the approximation of the Dirichlet problem for the Eikonal equation|∇u|=1 for arbitrary domains in two dimensions has been presented. We have introduced an iterative algorithm based on the following ingredients:a penalization of the non-smooth constraint on the gradient,a linear or nonlinear,biharmonic regularization of the variational problem,and an operator-splitting approach to find a stationary solution of the corresponding dynamical flow problem. Low-order finite elements have been used for the discretization,as the low regularity of the solution does not require any high-order approximations.Numerical results have shown the ability of our method in approximating solutions of the Eikonal equation for various twodimensional domains and various boundary data.In particular,our methodology can handle quite easily and accurately(convex)domains with curved boundaries.Cases with exact known solutions have allowed us to highlight the actual convergence properties of our methodology. Further work will include the extension of this Eikonal equation to the vectorial case,namely,to find u:R2→R2satisfying whereO(2)denotes the set of the 2×2 orthogonal matrices.This problem arises in the origami theory(see for instance[15–17]).The authors believe that the approach proposed in this article will apply naturally to this vectorial extension. AcknowledgmentsThe authors would like to thank Prof.Dacorogna B.(EPFL)for fruitful discussions and suggesting the investigation of such non-smooth problems.The first author thanks Prof.Picasso M.and MATHICSE(EPFL)for partial financial support. [1]Aronsson,G.,Evans,L.C.and Wu,Y.,Fast/slow diffusion and growing sandpiles,Journal of Differential Equations,131,1996,304–335. [2]Barth,T.J.and Sethian,J.A.,Numerical schemes for the Hamilton-Jacobi and level set equations on triangulated domains,J.Comput.Phys.,145(1),1998,1–40. [3]Caboussat,A.and Glowinski,R.,A numerical method for a non-smooth advection-diffusion problem arising in sand mechanics,Commun.Pure Appl.Anal,8(1),2008,161–178. [4]Caboussat,A.and Glowinski,R.,Regularization methods for the divergence equation∇·u=f,J.Comput.Math.,30(4),2012,354–380. [5]Caboussat,A.,Glowinski,R.and Pan,T.W.,On the numerical solution of some Eikonal equations:An elliptic solver approach,to appear of Contemporary Applied Mathematics,Higher Education Press,Beijing and World Scientific,Singapore,2013. [6]Caboussat,A.,Glowinski,R.and Sorensen.,D.C.,A least-squares method for the numerical solution of the Dirichlet problem for the elliptic Monge-Ampre equation in dimension two,ESIAM:Control,Optimization and Calculus of Variations,19(3),2013,780–810. [7]Caffarelli,L.and Crandall,M.G.,Distance functions and almost global solutions of Eikonal equations,Comm.Partial Differential Equations,3,2010,391–414. [8]Caffarelli,L.A.and Cabré,X.,Fully Nonlinear Elliptic Equations,American Mathematical Society Colloquium Publications,43,Providence,RI,1995. [9]Caffarelli,L.A.and Glowinski,R.,Numerical solution of the Dirichlet problem for a Pucci equation in dimension two.Application to homogenization,J.Numer.Math.,16(3),2008,185–216. [10]Chan,T.and Shen,J.,Image Processing and Analysis:Variational,PDE,Wavelet,and Stochastic Methods,SIAM,Philadelphia,2005. [11]Crandall,M.,Evans,L.and Lions,P.L.,Some properties of viscosity solutions of Hamilton-Jacobi equations,Trans.Amer.Math.Soc.,282,1984,487–502. [12]Dacorogna,B.,Glowinski,R.,Kuznetzov,Y.and Pan,T.W.,On a conjuguate gradient/Newton/penalty method for the solution of obstacle problems.application to the solution of an Eikonal system with Dirichlet boundary conditions,Kek,M.,Neittaanmki,P.,Glowinski,R.and Korotov,S.,editors,Conjugate Gradient Algorithms and Finite Element Methods,Springer-Verlag,Berlin,Heidelberg,2004,263–283. [13]Dacorogna,B.,Glowinski,R.and Pan,T.W.,Numerical methods for the solution of a system of Eikonal equations with Dirichlet boundary conditions,C.R.Acad.Sci.Paris,Sér.I,336,2003,511–518. [14]Dacorogna,B.and Marcellini,P.,Implicit Partial Differential Equations,Birkhaser,Basel,1999. [15]Dacorogna,B.,Marcellini,P.and Paolini,E.,An explicit solution to a system of implicit differential equations,Ann.Inst.Henri Poincaré,Analyse Non Linéaire,25,2008,163–171. [16]Dacorogna,B.,Marcellini,P.and Paolini,E.,Lipschitz-continuous local isometric immersions:Rigid maps and origami,Journal Math.Pures Appl.,90,2008,66–81. [17]Dacorogna,B.,Marcellini,P.and Paolini,E.,Origami and partial differential equations,Notices of the American Math.Soc.,57,2010,598–606. [18]Dean,E.J.and Glowinski,R.,Numerical methods for fully nonlinear elliptic equations of the Monge-Ampère type,Comp.Meth.Appl.Mech.Engrg.,195,2006,1344–1386. [19]Dean,E.J.and Glowinski,R.,On the numerical solution of the elliptic Monge-Ampre equation in dimension two:A least-squares approach,in Glowinski,R.and Neittaanmki,P.,editors,Partial Differential Equations:Modeling and Numerical Simulation,16,Computational Methods in Applied Sciences,Springer-Verlag,2008,43–63. [20]Dean,E.J.,Glowinski,R.and Guidoboni,G.,On the numerical simulation of Bingham visco-plastic flow:Old and new results,Journal of Non Newtonian Fluid Mechanics,142,2007,36–62. [21]Delbos,F.,Gilbert,J.C.,Glowinski,R.and Sinoquet,D.,Constrained optimization in seismic ref l ection tomography:A Gauss-Newton augmented Lagrangian approach,Geophysical Journal International,164,2006,670–684. [22]Evans,L.C.,Partial Differential Equations,19,Graduate Texts in Mathematics,American Mathematical Society,1998. [23]FlÜck,M.,Hofer,T.,Picasso,M.,et al.,Scientific computing for aluminum production,Int.J.Numer.Anal.and Modeling,6(3),2009,489–504. [24]Glowinski,R.,Finite Element Method for Incompressible Viscous Flow,IX,Handbook of Numerical Analysis(Ciarlet,P.G.,Lions,J.L.,eds),Elsevier,Amsterdam,2003,3–1176. [25]Glowinski,R.,Numerical Methods for Nonlinear Variational Problems,Springer-Verlag,New York,NY,2nd edition,2008. [26]Glowinski,R.,Numerical methods for fully nonlinear elliptic equations,Invited Lectures,6th Int.Congress on Industrial and Applied Mathematics,EMS,ZÜrich,Switzerland,2009,155–192. [27]Glowinski,R.,Kuznetzov,Y.and Pan,T.W.,A penalty/Newton/conjugate gradient method for the solution of obstacle problems,C.R.Acad.Sci.Paris,Sér.I,336,2003,435–440. [28]Glowinski,R.,Lions,J.L.and Trémolières,R.,Numerical Analysis of Variational Inequalities,Studies in Mathematics and Its Applications,North-Holland Publishing Co.,Amsterdam,New York,1981. [29]Gremaud,P.A.and Ide,N.R.,Computation of nonclassical solutions to Hamilton-Jacobi problems,SIAM J.Sci.Comput.,21,1999,502–521. [30]Gremaud,P.A.and Kuster,C.M.,Computational study of fast methods for the Eikonal equation,SIAM J.Sci.Comp.,27,2006,1803–1816. [31]Hysing,S.R.and Turek,S.,The Eikonal equation:Numerical efficiency vs algorithmic complexity on quadrilateral grids,Proceedings of Algorithmy,2005,22–31. [32]Kimmel,R.and Sethian,J.A.,Computing geodesic paths on manifolds,Proceedings of National Academy of Sciences,95(15),1998,8431–8435. [33]Majava,K.,Glowinski,R.and Kärkkäinen,T.,Solving a non-smooth eigenvalue problem using operatorsplitting methods,International Journal of Computer Mathematics,84(6),2007,825–846. [34]Nečas,J.,Introduction to the Theory of Nonlinear Elliptic Equations,John Wiley&Sons,Ltd.,Chichester,1986. [35]Prigozhin,L.,Sandpiles and rivers networks:Extended systems with nonlocal interactions,Phys.Rev.E,49(2),1994,1161–1167. [36]Prigozhin,L.,Variational model of sandpile growth,Euro.Journal of Applied Mathematics,7,1996,225–235. [37]Qin,F.,Luo,Y.,Olsen,K.,et al.,Finite-difference solution of the Eikonal equation along expanding wavefronts,Geophysics,57(3),1992,478–487. [38]Rockafellar,R.T.,Convex Analysis,Princeton University Press,Princeton,NJ,1997. [39]Schlichting,H.and Gersten,K.,Boundary Layer Theory,McGraw and Hill,8th revised edition,Springer-Verlag,Berlin,2000. [40]Sethian,J.A.,Fast marching methods,SIAM Rev.,41(2),1999,199–235. [41]Sethian,J.A.and Vladimirsky,A.,Fast methods for the Eikonal and related Hamilton-Jacobi equations on unstructured meshes,Proceedings of National Academy of Sciences,11,2000,5699–5703. [42]Zhao,H.,A fast sweeping method for Eikonal equations,Math.Comp.,74,2005,603–627.5 A Variant with a Nonlinear Biharmonic Regularization

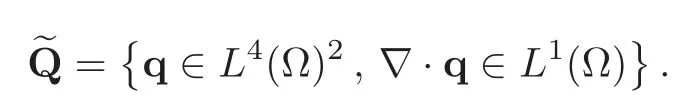



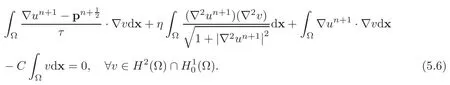

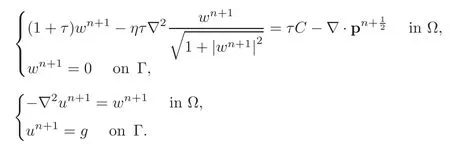
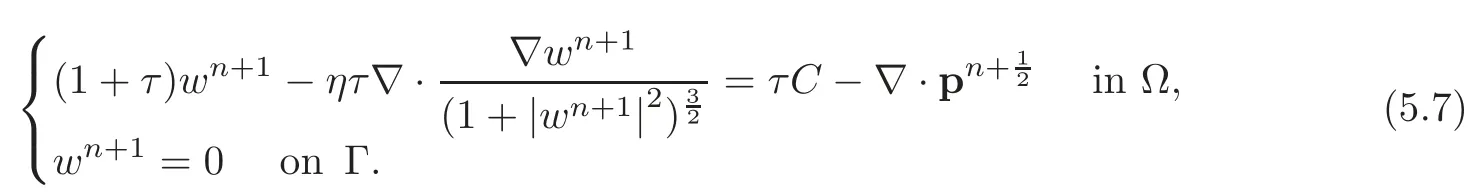
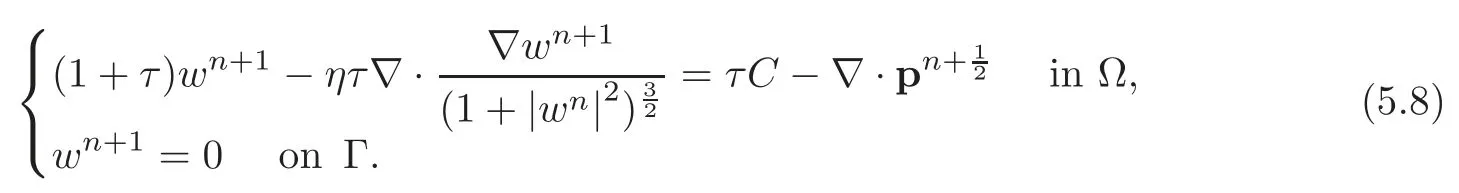
6 Finite Element Discretization
6.1 Generalities


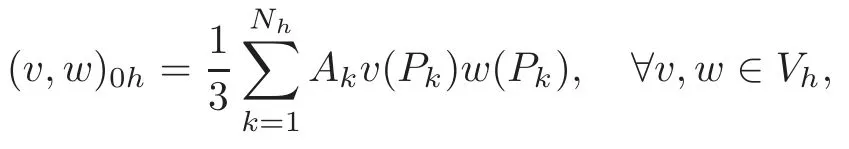
6.2 Approximation of the regularized variational problem


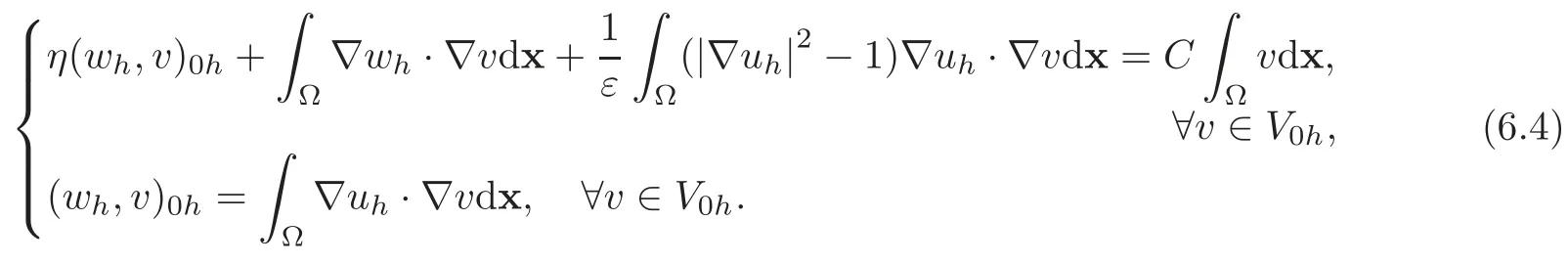

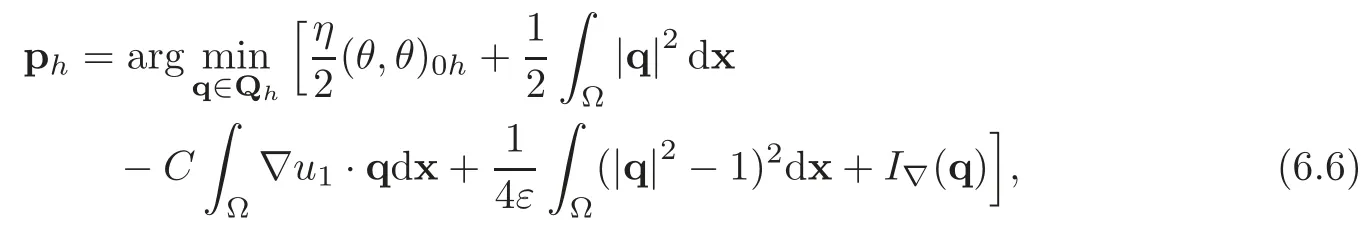






6.3 Initial-value problem and operator-splitting
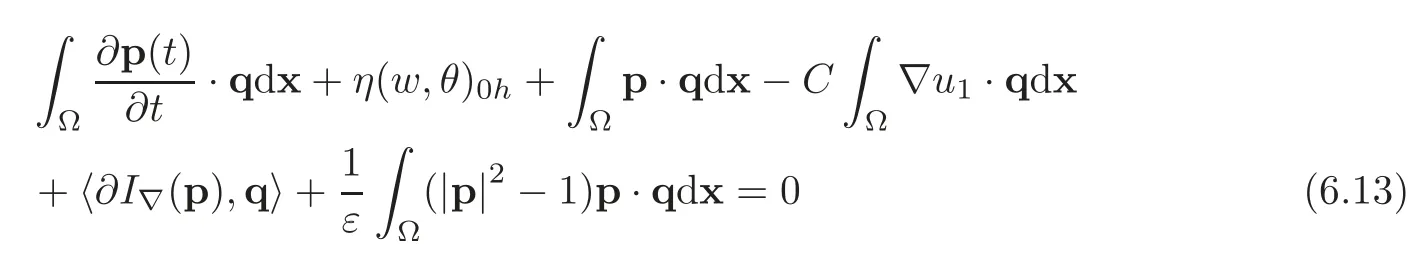


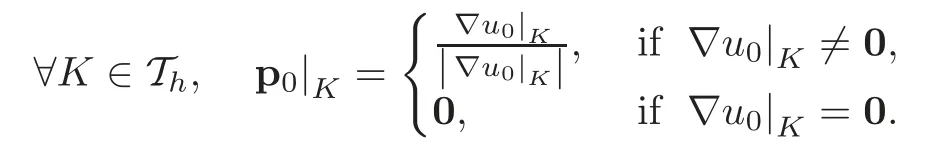
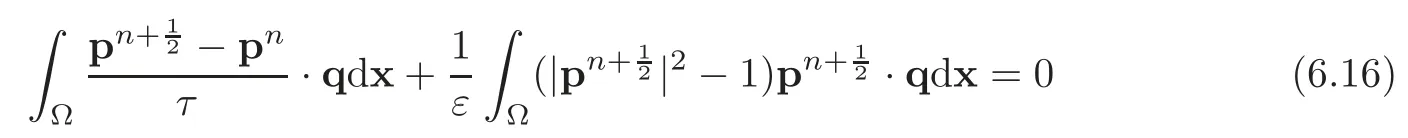

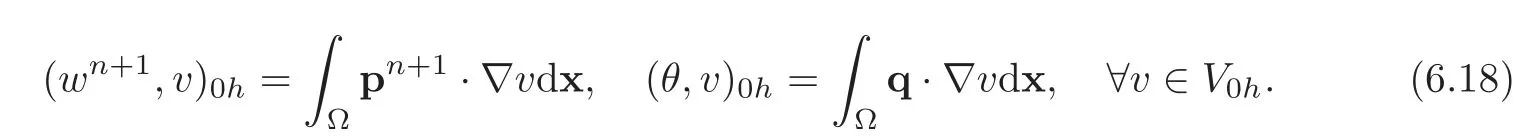
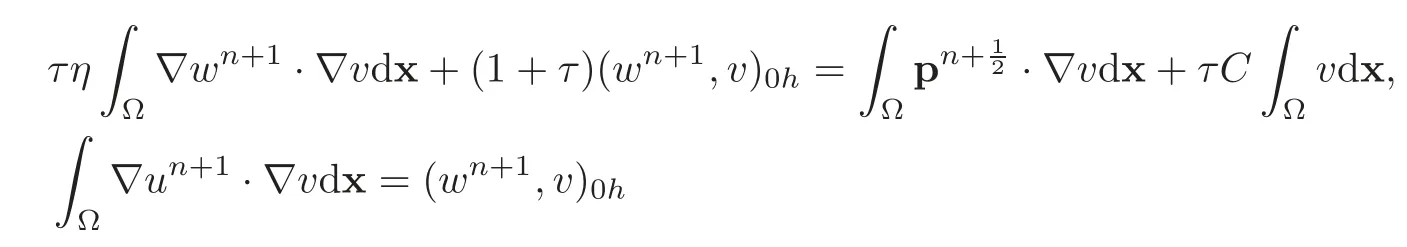
6.4 On the solution of the discrete nonlinear problems
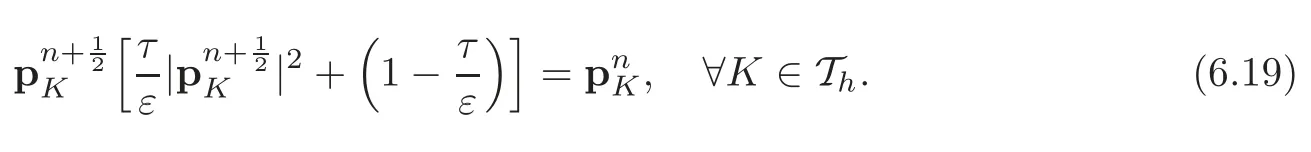
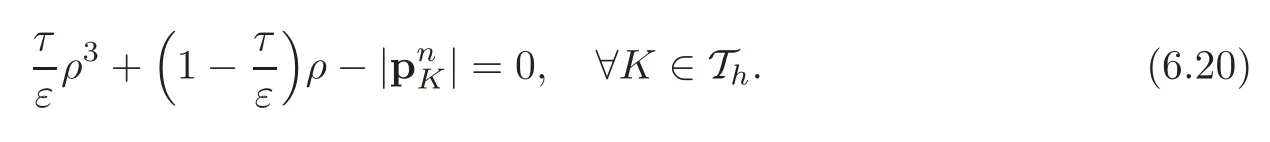
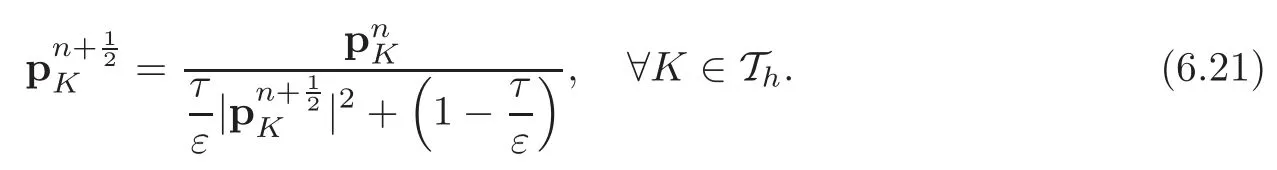
6.5 Further comments
7 Numerical Experiments
7.1 Solution of the Eikonal equation with homogeneous boundary conditions on the unit square(recovery of the distance function)




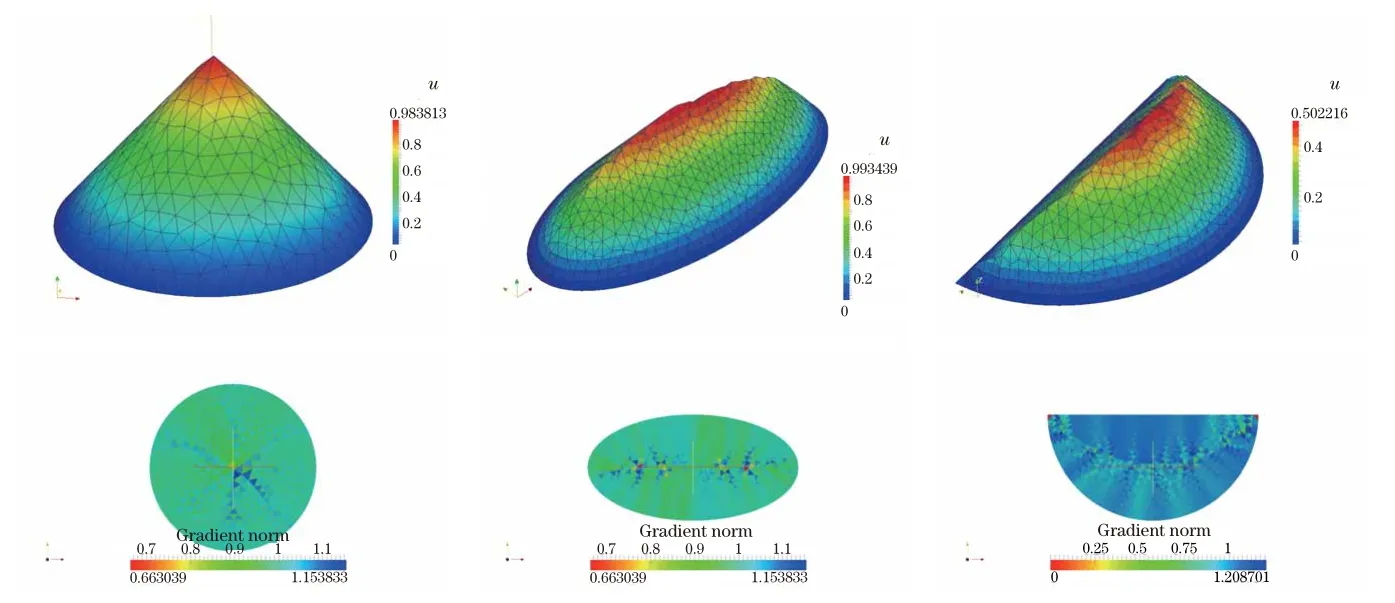
7.2 Solution of the Eikonal equation with homogeneous boundary conditions on two-dimensional domains with curved boundary(recovery of the distance function)
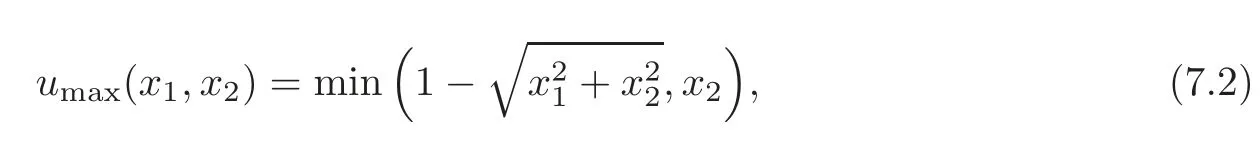


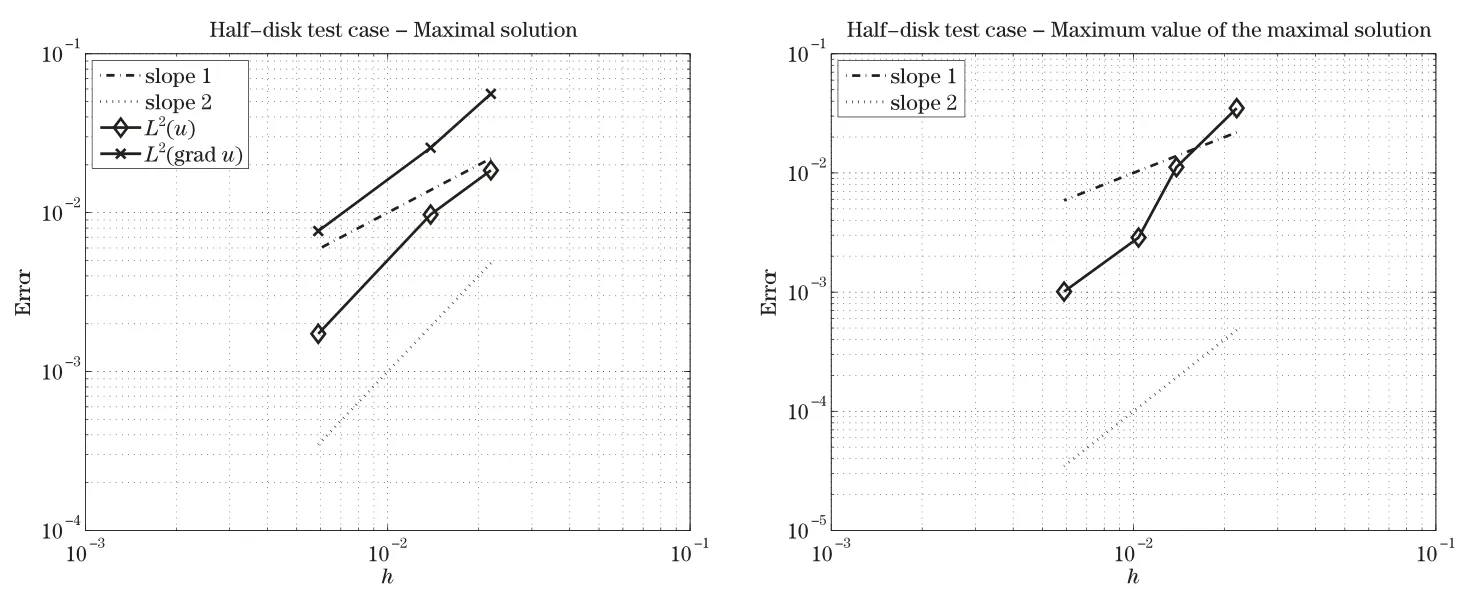
7.3 Solution of the Eikonal equation with non-homogeneous boundary conditions on the unit square(I)
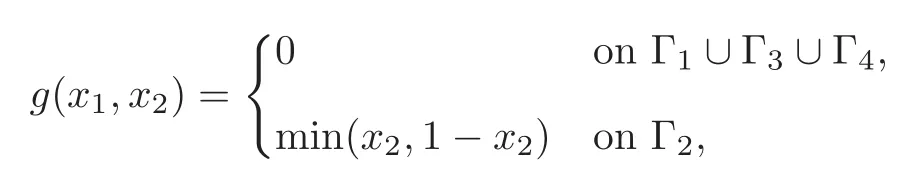

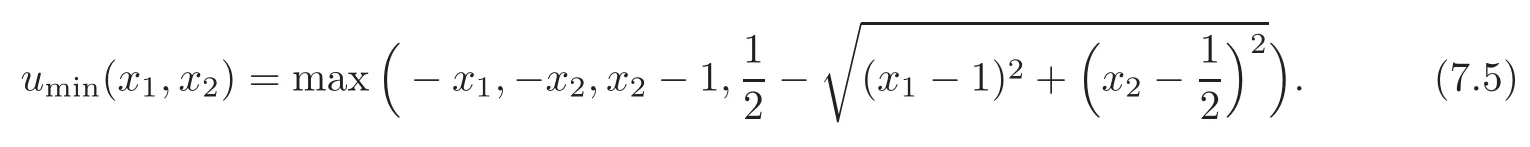



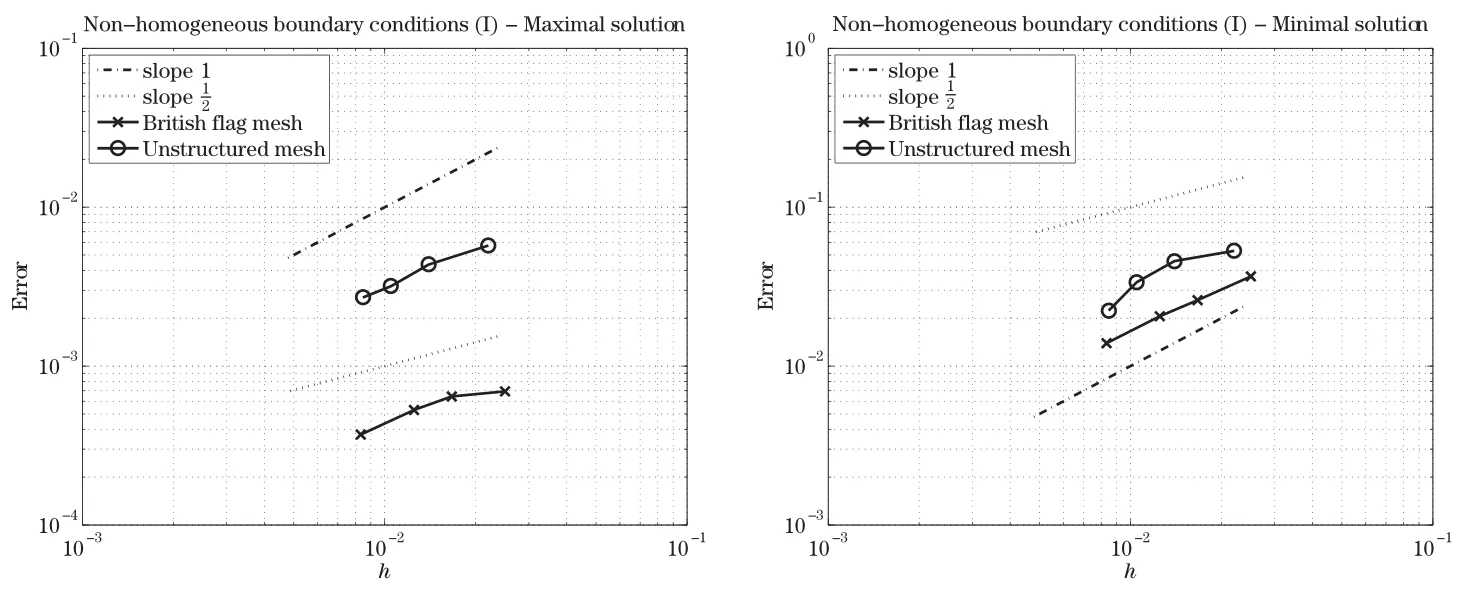
7.4 Solution of the Eikonal equation with non-homogeneous boundary conditions on the unit square(II)





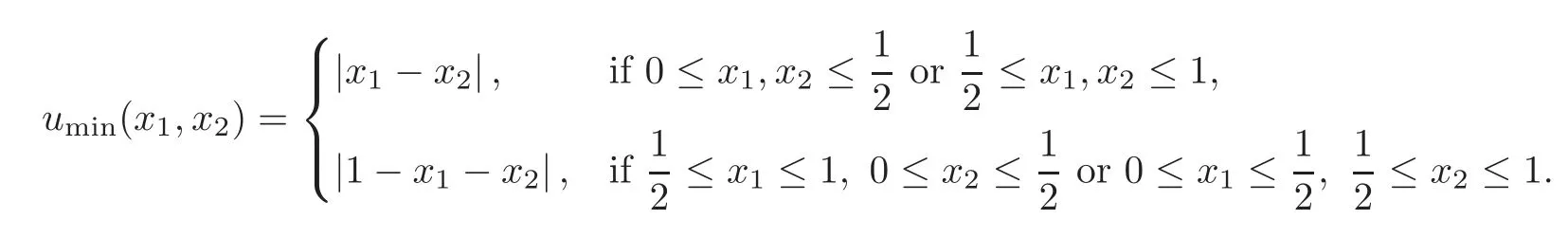

7.5 Solution of the Eikonal equation with non-homogeneous boundary conditions on the unit square(III):Incompatible boundary conditions
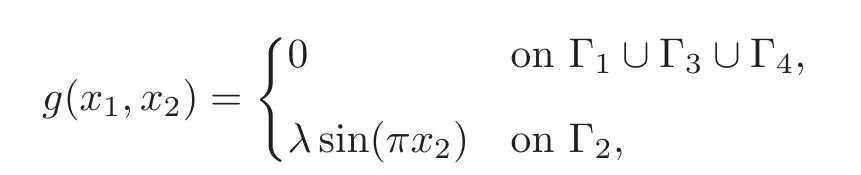


7.6 A CFD application
8 Viscosity Solution Interpretation
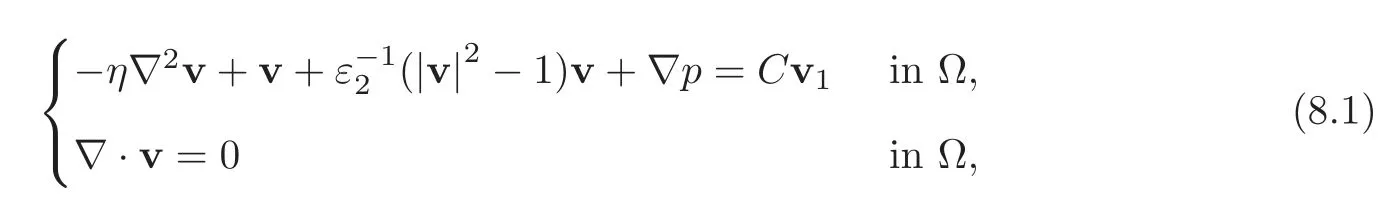
9 Concluding Remarks and Perspectives
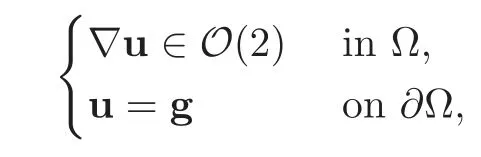
 Chinese Annals of Mathematics,Series B2015年5期
Chinese Annals of Mathematics,Series B2015年5期
- Chinese Annals of Mathematics,Series B的其它文章
- Long-Time Turbulence Model Deduced from the Navier-Stokes Equations∗
- Transversal Instability for the Thermodiffusive Reaction-Diffusion System∗
- Thermal Creep Flow for the Boltzmann Equation
- An Optimal Design Method Based on Small Amplitude Homogenization∗
- Pressure Boundary Conditions for Blood Flows
- The Role of a Vanishing Interfacial Layer inPerfect Elasto-Plasticity
