数学解题训练的两个“方程式”
何南荣 钟结枚 王海青

【摘要】数学解题训练是数学学习与数学教学的核心环节. 本文通过对数学解题结构的认知,建立数学解题训练的深广度“方程式”和思维导图“方程式”,有效地提高中学生分析和解决问题能力、数学发散思维能力和创新能力,进而达到解题训练的效果. 实践结果表明,其可行性和解答率均相对较高.
【关键词】深广度;思维导图;数学解题;解题训练
随着数学教育改革的不断深入,如何培养学生的数学学习能力和创新能力已成为数学教育界讨论的重大课题. 处在高考模式下的中学生的创新能力偏低现象已愈趋严重,亟待改革. 在数学学习和教学当中,解题训练对于数学的认知,提高数学思维能力,培养创新能力起着重要的作用,因此,对数学解题训练的方法展开研究对数学教学和学习的改革有着深远的意义. 目前,国内外已提出许多不同层次的解题策略,如波利亚等人已有大量而系统的数学解题的研究成果,但对于如何进行解题训练来说,其方法仍然达不到更加具体的训练效果. 本文力求适于目前中学生学习和教师教学的基本状况,对波利亚的解题方法加以改进优化,望能为教学改革和学习方法带来更好的帮助,让中学生在解题训练中更大程度上提高数学思维能力和培养创新能力.
一、数学解题的结构认知
数学解题过程就是获取信息、转换信息和实现目标信息的过程,具体是根据已知的条件信息,以目标信息为目的,在知识储备中以最熟悉的方式进行全局搜索,找出条件与目标的最佳匹配方式的过程.
数学解题结构虽清晰明了,但“解题难”的现象在数学学习和教学当中早已司空见惯,究其原因主要由知识点的牢固程度、知识网络结构的构建程度、题型的量度和熟练程度、分析和思考的方向等五大方面造成,因此,克服“解题难”问题应从这五方面展开探究,再结合波利亚的《怎样解题》,本文认为:一个完整的解题过程必须具备六大条件,即:
知识储备:缺乏一定的知识量和知识网络结构,解题便无法进行. 只有储备大量的基本知识点和构建知识网络结构的基础上,才能搭建解题的基本支架.
积极心态:对于复杂繁多的问题,往往会眼花缭乱,挫败解题信心,干扰解题思维和判断. 因此,在解题之前应给予自己积极的心理作用,需找到一种战斗而自信的状态,如“我是肯定行”等. 当然,遇到不会的问题,亦要有恰当的心理暗示,如“不会的问题才是解题训练的理由”等.
理清问题:理清问题中显示和隐藏的条件并尝试建立条件之间的联系,弄清要解决什么问题,将其罗列出来,问题变得更清晰.
搜索方案:结合自己已有的知识,将条件和目标转换为最熟悉的数学表达方式,而后搜索出条件与目标最佳的匹配方式(即建立条件与目标的关系). 当所有条件都用上之时,解题便成功一大半,故在匹配过程中注意用上所有条件.
目标实现:找到匹配方式之后,用数学专业术语详略得当的将准确无误的思路和计算结果淋漓尽致地表述出来.
反思总结:反思就是在解题之后思考“为什么想不到”“错在哪里”或“自己应该怎样改正”等. 总结即是将自己在解题过程中不会的知识点、转折点或奇妙之处等总结描述出来,并在更深层次上理解和熟练解题技巧.
二、数学解题的两个“方程式”
对于中学生和中学教师来说,数学解题训练是其数学学习和数学教学的核心环节,其主要通过解题训练获取相关知识、锻炼分析和解决问题的能力、培养良好的数学思维和独特的创新能力等. 因此,在解题训练的过程中,应注重训练方法的恰当性. 本文在解题结构的六大条件的基础上提出下面解题训练的两个基本模式.
1.数学解题训练的深广度“方程式”
本文认为:一个完整、系统的数学解题是通过深广度来分析和解决数学问题,即给定一道数学题,先通过广度思考如何分析和解决问题,进而尝试发散思维找出不同的解法;通过深度思考针对相应的问题条件尝试提出多种更深层次的问题并能用类似方法解决. 因此,一个完整、系统的数学解题训练的“方程式”是由深度思考和广度思考两个支架构成.
解题训练是一种过程,并不在于能否完全解决问题,只要按照解题深广度“方程式”进行,再加以思考后参考,亦能达到解题训练的效果. 在解题训练中,通过上面方程式的训练,可实现举一反三的效果,巩固基本知识点和相关题型的量度及熟练程度;以一种寻找和探索标新立异、发散的思维方式进行解题,培养学生的分析和创新能力.
解决数学问题难,但有时提出数学问题更难,通过上面“方程式”的建立,也可很好地在“提出问题难”和“解题难”的问题中得到有效的训练,有效地实现数学学习的本质目标,即提出和解决数学问题.
2.数学解题训练的思维导图“方程式”
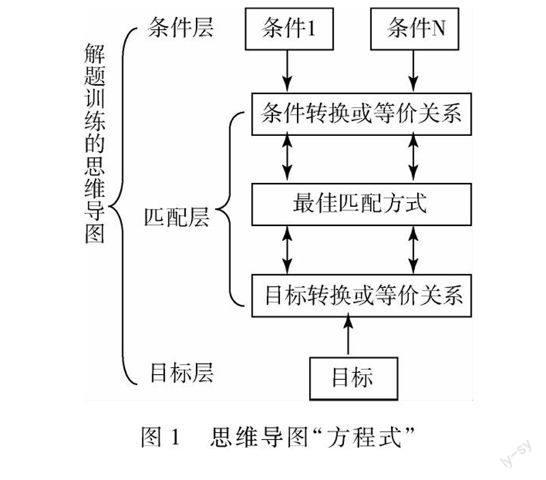
为了在更大程度上简化问题的难度和更好地实现解题效果,本文以数学解题的结构认知中六大解题条件为基础,建立数学解题的思维导图“方程式”:
图1 思维导图“方程式”
数学解题训练的思维导图“方程式”是一种有效地简化问题难度的“方程式”,可在一定的知识储备的基础上理清问题的条件信息和目标信息,并用积极的心态有效地简化问题难度,较为直观地进行搜索最佳的匹配方式,最后进行反思总结,从而达到高效的解题训练效果. 当熟练思维导图“方程式”到一定程度之时,便无须一一罗列,可直接进入最优的解题方式的状态.
三、例谈两个“方程式”在解题中的应用
在数学解题训练的过程中,以解题深广度作为思维训练蓝图,以数学解题思维导图作为解题训练具体执行者,可高效地实现基础题型的解答,有效实现训练效果.
例 在△ABC中,CA⊥CB,OA=(0,-2),点M在y轴上且AM=12AB+AC,点C在x轴上移动.
(1) 求B点的轨迹E的方程;
(2) 过点F0,-14的直线l交轨迹E于H,G两点,(H在F,G之间),若FH=12HG,求直线l的方程.
目标层:B点的轨迹E的方程转换设B点坐标为x,y,建立x与y的关系.
匹配层:结合条件相应地转换以及观察它们之间的联系,发现x0,y0,x,y之间已交错建立起等价关系,只需用代入法将其转化为问题的目标,即x与y的关系便可求解.
解析 (1) 将④代入①,可得其关系y=x2(x≠0),所以,点B的轨迹E的方程为y=x2(x≠0);同理将④、⑤分别代入①、②、③,亦可得y=x2(x≠0),所以,点B的轨迹E的方程为y=x2(x≠0),总共有6种解法.
(2)与上题一样,本文找到四种相应的解法(除常规解法外,也可由A点在准线上,利用准线的性质求解),因而,可得到满足条件的两条直线,其方程分别为:8x+43y+3=0,8x-43y-3=0.
深度思考
(1)①如图1所示,在△ABC中,其条件与上题(1)一样. 假设BC是一对情侣,BC的距离定义为容忍度,当BC距离越大时,表示其越不能容忍对方,当越接近时,表示越容忍对方,请建立数学模型说明双方在什么时候才会在一起?(其模型实际上就是求轨迹问题,目标是找到B和C轨迹的交点,把应用和建模引进数学教学中,有利于培养学生应用能力)
②在长方形ABCD中,CA⊥CB,OA=(0,-2),点M在y轴上且AM=12AB+AC,点C在x轴上移动,试求D点的轨迹.(先求B点轨迹,再建立B和D的关系而求得)
(2)①过点F0,-14的直线l交轨迹E于H,G两点(H在F,G之间),若FH=12HG,求直线l的方程.(解法与(2)的解法类似)
②过点F0,-14的直线l交轨迹E于H,G两点(H在F,G之间),设轨迹E的焦点I,若HI=12GI,求直线l的方程.(解法与(2)的解法类似)
反思与总结 本题中的(x≠0)是经常忽略的细节,不易发现的原因是没有整体上分析此题,注意函数问题中的定义域和值域优先考虑的原则;通过不断地联想之前所学过的知识,建立好匹配方式,解决此问题的关键是对基本的数学概念和性质熟悉程度,需加强这方面的训练.对于本题所要熟悉的知识点是:几何向量与坐标之间的转换关系和圆锥曲线的性质等.
【参考文献】
[1]李大勇. 数学解题模式教学与数学能力的培养[J].黔东南民族师范高等专科学校学报,2004,22(3):10-11.
[2]毛志挺. 关于中学数学解题策略的认识和思考[J]. 浙江师范大学学报,2002,25(1):98-101.
[3]波利亚.怎样解题[M]. 北京:科学出版社,1982.

