推理与证明、算法和复数命题规律与备考策略

高慧明 张琦

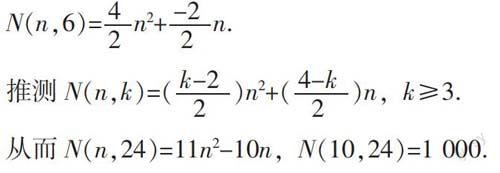
推理与证明一般与数列、几何、等有关内容融合在一起考查.本部分内容是高考的新增内容，主要以选择填空的形式出现，难度上属中偏低档题.新课标下把猜想、合情推理、类比推理与递推数列等内容结合是试题的一个亮点，合情推理的考查仍将为高考的重点和热点之一，因此要重视对合情推理的训练.同时本单元是培养同学们良好思维习惯，学习和运用数学思想方法，形成数学能力的重要重要内容，但建议考生不必要去做过难的题目.

算法初步在原高中数学教学大纲中无此内容，是新课程高考的新增内容.主要以客观形式题出现.考查考生的算法思想.算法主要包括三种基本结构：顺序结构、选择结构和循环结构，考试中考查最多的是循环结构.常见的题型有两种：一种是阅读算法程序框图，写出执行结果;第二种是已知程序框图的执行结果，填写算法框图的空白部份.近几年的高考中，每年都有考查，一般每份试卷有一道算法题，且多以选择题、填空题等中低档题的形式出现.试题主要考查算法含义、算法语句、程序框图等内容，热点主要体现在程序框图上，试题背景多与函数、数列、三角、实际问题等知识进行整合，是试题命制的新亮点.

复数在高考中年年有题，而且所占份量不少，都是一些中低档易得分的常规题.因此我们在备考复习中，一定要注意把握好其重点及其题型.首先要熟悉考查的知识要点：概念、复数的表示方法、几何意义、复数运算法则、复数的基本性质等.其次要掌握重要题型：复数的运算、求复数的模、复数的加、减、乘、除运算的几何意义及其应用.预计这些问题还将是今后高考命题的热点，希望引起考生重视.

第一单元 合情推理与演绎推理

【考点聚焦】

本单元内容主要包括归纳推理和类比推理和演绎推理.其中归纳推理和类比推理统称为合情推理.

【经典解析】

考点1：归纳推理

例1.（2015年高考山东理科）观察下列各式：

【收获与点评】归纳推理是由部分到整体、由特殊到一般的推理，由归纳推理所得的结论不一定正确，通常归纳的个体数目越多，越具有代表性，那么推广的一般性命题也会越可靠，它是一种发现一般性规律的重要方法.               .

【思维生长点】本题需要通过观察已知的N（n，3），N（n，4），N（n，5），N（n，6）的展开式中n2的系数，发现是等差数列，进而能够得到N（n，k）展开式中n2的系数.而进一步研究能够发现，N（n，3），N（n，4），N（n，5），N（n，6）的展开式中n2与n的系数之和为1，所以可得n的系数.

【收获与点评】进行归纳推理，所得到的结论都不一定正确，其结论的正确性是需要证明的.但是在一般情况下，如果归纳的个别事物越多，越具有代表性，那么推广的一般性结论也就越可靠.

考点2：类比推理

【收获与点评】演绎推理是从一般到特殊的推理;其一般形式是三段论，应用三段论解决问题时，应当首先明确什么是大前提和小前提，如果前提是显然的，则可以省略.

考点4：新定义下的归纳推理

【收获与点评】①逆向思考是用分析法证题的主要思想，通过反推，逐步寻找使结论成立的充分条件.正确把握转化方向是使问题顺利获解的关键.②证明较复杂的问题时，可以采用两头凑的办法，即通过分析法找出某个与结论等价（或充分）的中间结论，然后通过综合法证明这个中间结论，从而使原命题得证.

考点3：反证法的应用

【收获与点评】用反证法证明不等式要把握三点：①必须先否定结论，即肯定结论的反面;②必须从否定结论进行推理，即应把结论的反面作为条件，且必须依据这一条件进行推证;③推导出的矛盾可能多种多样，有的与已知矛盾，有的与假设矛盾，有的与已知事实矛盾等，且推导出的矛盾必须是明显的.

例4. 直线y=kx+m（m≠0）与椭圆W：+y2=1相交于A，C两点，O是坐标原点.

（Ⅰ）当点B的坐标为（0，1），且四边形OABC为菱形时，求AC的长;

（Ⅱ）当点B在W上且不是W的顶点时，证明：四边形OABC不可能为菱形.

【思维生长点】（I）先根据条件得出线段OB的垂直平分线方程，从而可求得A、C的坐标，根据两点间的距离公式即可得出AC的长;（II）欲证明四边形OABC不可能为菱形，只须证明若OA=OC，则A、C两点的横坐标相等或互为相反数.设OA=OC=r，则A、C为圆x2+y2=r2与椭圆+y2=1的交点，从而解得则A、C两点的横坐标相等或互为相反数.于是结论得证.

所以四边形OABC不是菱形，与假设矛盾.

所以当点B不是W的顶点时，四边形OABC不可能为菱形.

【收获与点评】①掌握反证法的证明思路及证题步骤，明确作假设是反证法的基础，应用假设是反证法的基本手段，得到矛盾是反证法的目的;②当证明的结论和条件联系不明显、直接证明不清晰或正面证明分类较多、而反面情况只有一种或较少时，常采用反证法;③利用反证法证明时，一定要回到结论上去.

第三单元 数学归纳法及其应用

【考点聚焦】

本单元内容就就是数学归纳法及其应用.

数学归纳法的框图表示（如上页图）.

考点1：用数学归纳法证明等式

例1. 已知等差数列{an}的公差为3，其前n项和为Sn，等比数列{bn}的公比为2，且a1=b1=2.

（Ⅰ）求数列{an}与{bn}的通项公式;

（Ⅱ）记Tn=anb1+an-1b2+…+a1bn，n∈N*，证明Tn+12=-2an+10bn（n∈N*）.

【思维生长点】（Ⅰ）代入等差、等比数列的通项公式求an，bn;（Ⅱ）注意到所证结论是关于“n”的命题，可运用数学归纳法证明.

由①②可知，对任意n∈N*，Tn+12=-2an+10bn成立.

【收获与点评】①用数学归纳法证明等式问题，要“先看项”，弄清等式两边的构成规律，等式两边各有多少项，初始值n0是多少.②由n=k时等式成立，推出n=k+1时等式成立，一要找出等式两边的变化（差异），明确变形目标;二要充分利用归纳假设，进行合理变形，正确写出证明过程.

考点2：用数学归纳法证明不等式

【收获与点评】用数学归纳法证明不等式的关键是由n=k时命题成立证n=k+1时命题也成立，在归纳假设使用后可运用比较法、综合法、分析法、放缩法等来加以证明，充分应用基本不等式、不等式的性质等放缩技巧，使问题得以简化.

考点3：归纳——猜想——证明

【收获与点评】“归纳-猜想-证明”的模式，是不完全归纳法与数学归纳法综合应用的解题模式，这种方法在解决探索性问题、存在性问题时起着重要作用，它的模式是先由合情推理发现结论，然后经逻辑推理证明结论的正确性.

第四单元 算法与程序框图

【考点聚焦】

本单元内容主要包括算法的含义、程序框图和基本算法语句.

考点1：基本逻辑结构

【收获与点评】此类问题的一般解法是严格按照程序框图设计的计算步骤逐步计算，逐次判断是否满足判断框内的条件，决定循环是否结束.要注意初始值的变化，分清计数变量与累加（乘）变量，掌握循环体等关键环节.

考点2：程序框图的识别与应用问题

【收获与点评】识别、运行程序框图和完善程序框图的思路要注意以下三点：①要明确程序框图的顺序结构、条件结构和循环结构.②要识别、运行程序框图，理解框图所解决的实际问题.③按照题目的要求完成解答并验证.

考点3：基本算法语句

例3. （Ⅰ）根据图1算法语句，当输入x为60时，输出y的值为（ ）

A. 25           B. 30           C. 31           D. 61

（Ⅱ）根据图2的程序写出相应的算法功能为________.

解析：（Ⅰ）通过阅读理解知，算法语句是一个分段函数y=f（x）=0.5x，x≤50，25+0.6×（x-50），x>50，

∴ y=f（60） = 25+0.6×（60-50） = 31.

（Ⅱ）该程序是计算1～999中连续奇数的平方和.

【收获与点评】输入、输出和赋值语句是任何一个算法必不可少的语句，一个语句可以输出多个表达式.在赋值语句中，一定要注意其格式的要求，如“=”的右侧必须是表达式，左侧必须是变量;一个语句只能给一个变量赋值;变量的值始终等于最近一次赋给它的值，先前的值将被替换;条件语句的主要功能是实现算法中的条件结构，解决像“判断一个数的正负”“比较两个数的大小”“对一组数进行排序”“求分段函数的函数值”等问题，计算时就需要用到条件语句.

第五单元   复数

【考点聚焦】

本单元内容主要包括复数的基本概念，复数相等的充要条件，复数的代数表示法及其几何意义，复数代数形式的四则运算，复数代数形式的加、减运算的几何意义.

考点4：复数的概念

【收获与点评】在做复数的除法时，要注意利用共轭复数的性质：若z1，z2互为共轭复数，则z1·z2=|z1|2=|z2|2，通过分子、分母同乘以分母的共轭复数将分母实数化.

复数相等是一个重要概念，它是复数问题实数化的重要工具，通过复数的代数形式，借助两个复数相等，可以列出方程（组）来求未知数的值.复数问题要把握一点，即复数问题实数化，这是解决复数问题最基本的思想方法.

（作者单位：北京市第十二中学）

责任编校   徐国坚