初中数学函数应用题解题策略研究
张安飞
【摘要】 初中数学是学生数学学习的重要阶段,也是打下坚实根基的决定性阶段. 在初中数学课程中,函数占据了很大的份额,是初中数学的主要内容之一. 初中数学中的函数应用题是函数的主要类型题,针对这种题型,应当明确应用题的解题思路,对每一步解题思路都能够联想到其理论内容,对于数学函数应用题来说具有重要意义. 本文就初中数学函数应用题的解题策略进行了分析与探究.
【关键词】 初中数学;函数应用题;解题思路策略
解题思路对于数学题而言是必不可少的环节,是解答出数学题的重要部分. 只有明确理出数学的解题思路,才能够为数学题的解决提供条件. 每种数学题的解题思路会随着题型的不同而发生变化,对于初中数学中的函数应用题,解题思路是构成函数数学题的重要部分,初中的函数类型为一次函数、二次函数以及反比例函数,对这种类型题先明确其解题思路是关键问题.
一、明确理解函数应用题的立意
明确理解函数应用题的立意是解出函数应用题的重要前提. 在解题之前,应当对函数题目进行反复的推敲,能够正确读懂立意,才不会因为理解偏题而导致错误的解析,严重影响解题效率和解题质量. 因此,在解初中函数应用题时,应当仔细阅读题目要求,因为根据应用题的特性,题目会比较长,容易模糊学生的解题思路,因此,应当正确审题,明确题目立意. 我们根据苏科版教材中的函数应用题进行了研究与分析.
例题1 某服装销售部门,一款衣服的进价为150元,当这件衣服的销售价为200元时,平均每个月能够售出20件,销售额每降低5元,每个月会多售出10件,设每件衣服的降价为x元,每件衣服的利润为y元,列出相应的函数关系式.
(1)如上题所示,首先明确题目的立意,是让求每件衣服的降价和利润之间的关系,根据这个要求我们可以得出:利润 = 销售价 - 降价 - 进价;
(2)根据这个公式我们可以出相关的x与y的函数关系式:y = 200 - x - 150 = -x + 50如果在商家不存在亏损的情况下x的取值为0 ≥ x ≥ 50.
二、重视函数基础内容的运用
函数的数学基础是解出函数数学题的基本保证. 由于初中函数应用题考察的内容偏向于基础知识,都是对基础知识的整合与深入,在扎实掌握初中数学函数的基础知识的基础上,进行函数应用题的解析,会感觉题目的难度系数并不是很高,重点考察学生的函数基础知识.
例如,在例题1中,如果是求平均每个月该服装的销售利润问题和最值问题,则是对基础知识的进一步整合. 设该款衣服平均每个月的销售利润为m元,求m与x之间的函数关系式以及x取何值时,平均每个月的销售利润最大.
(1)根据题意,我们首先应当求列出销售量的关系式为:20 + 10 × ■,而m = y20 + 10 × ■;
(2)有例题1可知,Y = -x + 50,那么m = (-x + 50)20 + 10 × ■ = -2x2 + 80x + 1000;
(3)关于求最值的问题,可以利用完全平方公式来求得,m = -2x2 + 80x + 1000 = -2(x - 20)2 + 1800. 当x = 20时,衣服的定价为200 - x = 180元,平均每个月的最大利润是1800元.
以上的题目就是对函数基础内容的考察,一个是最值问题,一个是函数的完全平方公式,函数应用题是各种函数基础知识的叠加,应当注重函数学习的基本功,让学生能够明确解题思路.
三、加强函数之间内容的联系
数学题中各个概念是相互聯系的,应当注重内容的相互联系,将内容进行整合,有利于数学知识的系统性学习. 数学的函数之间知识的连贯性很强,尤其是在函数应用题中,重视对函数综合能力的考察,涉及的内容很全面,将不同次项的函数以及最值问题进行综合考察,是现代函数应用题普遍存在的特点. 目前,初中数学函数应用题都是综合性很强的题目,重视对函数知识的整合,对解题思路的构建具有重要意义.
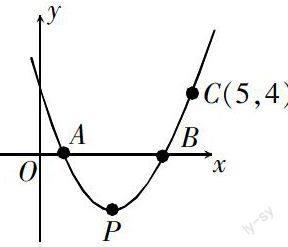
例题2 如图所示,已知抛物线y = ax2 - 5ax + 4a交于x轴的A、B两点,其中,C点的坐标为(5,4),求a值和顶点P的坐标.
(1)如图所示,已知C点的坐标(5,4),将点的坐标代入抛物线方程中能够求得a = 1. 由图所示,a > 0,因此,a = 1;
(2)由于a = 1,所以可以得出y = x2 - 5x + 4,根据题意可知该抛物线交于x轴,可以得出A(x1,0),B(x2,0),然后可以计算出x1和x2的值,x1 = 1,x2 = 4;
(3)由于P点是抛物线的顶点,P点的横坐标是A、B两点横坐标的中点,得出P的横坐标为2.5,将横坐标数据代入到抛物线方程中,得出P点的坐标为(2.5,-2.25).
以上这个题目既考查到了函数问题,同时还包括抛物线的坐标问题、顶点问题、系数问题,其中涉及的问题很多,内容之间存在着一定的联系,是构建解题思路的关键,应当重视对所学函数内容的整合,加强内容上的联想,对形成解题思路具有重要意义.
结束语
随着新课程的改革,函数在初中数学中占有的比重越来越大,是初中数学课程的重点和难点. 函数应用题是函数问题的升级题目,是对函数问题的综合考验,将一次函数、二次函数以及反比例函数进行考验,因此,明确函数题型的解题思路成为杰出函数应用题的关键. 因此,教师应在教学过程中注重对学生解题思路的锻炼,为解出函数应用题奠定基础.
【参考文献】
[1]王允.初中数学应用题教学的研究[J]. 科学之友. 2012,10(14):113-114.
[2]贾靖林.信息化环境下初中数学函数教学的策略研究[J].中国教育技术装备.2011,02(15):97-98.
[3]金道义.信息化环境下初中数学函数教学的策略研究[J].新课程学习(中).2012,11(18):73-74.
[4]陈雪霞.信息化环境下初中数学函数教学的策略研究[J].新课程学习(上).2014,02(08):70-71.

