“效”可以“问”出来

张波

【摘要】课堂提问是数学教学中不可缺少的重要手段，是师生交流的主要形式.新课程理念下的初中数学课堂教学，教师是组织者，引导学生在获取数学知识的过程中能积极主动地去感受、探究数学问题，从而获得数学认知能力和创新能力.这其中，教师的有效提问就起着关键的“导向”作用.本文就“初中数学课堂有效提问设计的原则”从设问、表述、难度、层次、兴趣、创新等六个方面来阐述笔者在教学实践中的一些粗浅体会与做法.

【关键词】初中数学；有效提问；设计原则

数学课堂中，有效提问是教学的关键，它不仅可以展现教师和数学的无形魅力，还可以让学生在广阔的思维宇宙中自由飞翔.“水本无华，相荡乃成涟漪； 石本无火，相击而发灵光.”打造高效数学课堂，也需要这样的“涟漪”和“灵光”，把握课堂有效提问设计的原则，巧妙提问，从而在创造性的头脑风暴中，活跃课堂气氛激发个体思考，启迪师生心智，提高课堂教学效率，促进学生健康发展

一、精心设问

教师要缜密考虑预设问题的基点.一个设计得好的问题既能激发学生对数学内容的学习兴趣，调动他们思考、解决问题的积极性，也可以引导学生的思考方向，扩大思维广度，提高思维层次，同时也有利于学生间的相互启发，促进师生间的交流.因此，课前缜密考虑问题的预设是实现有效数学教学的必要前提.为了保证课堂教学的有效性，教师必须明确所提出问题的目的.要明确每一个的问题的具体目的，是为了引起学生的学习兴趣、检查学生对已有知识的记忆，还是启发学生进行进一步的思考等等.教师要在备课时作出充分的考虑，否则在课堂上随机的发问，就会出现一些无效的问题，浪费宝贵的课堂时间.

例如：在讲授新课：“不在同一直线上的三点确定一个圆”.

问题1：过一点可画多少个圆？为什么？

问题2：过两点可画多少个圆？圆心的位置有什么规律？为什么？

问题3：过不在同一直线上三点A，B，C画圆，这样的圆要经过A，B，圆心在哪里？这样的圆又要过B，C，圆心在哪里？若同时经过A，B，C，圆心又在哪里？

问题4：这样的圆可画多少个？

教师单刀直入、层层设问、简单明了，学生动脑、动手，把自己作为“研究者”，逐步深入，将已有的知识、思维方法迁移到新知识中去，学得轻松，记得也牢.

二、表述准确

有效课堂提问的问题需表达清楚、简洁明了、无重复性，问题的水平与学生的知识水平相符.学生必须通过思考才能回答，教师的语调和其他肢体语言能充分的利用来促进学生的思考.教师能从学生的认知水平出发，以学生易于理解的语言来阐述问题，从学生的反应看，学生基本上都能很好的理解教师的问题.

例如：著名特级教师李庾南在讲解《因式分解》这节课时，描述因式分解的概念是和整式的乘法进行对比，说了很多遍的“反过来”.这是多么好的一句“白话文”，却是李老师“苦心经营”的一句话.很多老师在讲解因式分解概念时总是按照教材中的概念描述：把一个多项式化为几个整式的乘积的形式.学生对这里的“化为”也是一知半解，导致分解时总出现分解不彻底等现象.学生刚学完整式的乘法，紧接着就学习因式分解，必然受到思维定势的影响，搞不清二者的区别于联系.李老师的一句“反过来”，通俗易懂，学生乐于接受.例如，教学“异分母分式加减法”，引入1x+2-1x-2后提问：“1x+2，1x-2 这两个分式有什么特点？”显然，这一提问不准确，学生回答：“分子都是1”，显然是正确的，但回答没有达到教师的提问意图.如果改问：“这两个分式的分母相同吗？分母不同的分式能不能直接相加？为什么？”这样的提问既明确，又问在关键处，有助于学生理解为什么要通分的道理.

三、难度适中

教师在设计提问要把握好问题设计的难度，避免两类提问：一类是太简单，一类是太难.根据实际情况适当的调整使得问题的难度符合学生的认知水平.

有的教师喜欢问学生一些答案是显而易见的问题，比如“今天星期几？” “这个问题很显然是——对的”.这种问题不论是让全班齐答 ，还是让某个学生回答 ，都是很无聊的.此类问题问的太多，而且又面向全体学生 ，容易会使学生反感 ，思维懈怠.

反之难度太高的问题教师要严格控制，在课堂上要根据学生的反应适时调整，设置一些过渡性的问题，是学生顺利越过思维障碍的门槛.苏科版九下教材中有这样一道习题：如图，用一段长20 m的铝合金型材制作一个矩形窗框，窗框的长和宽各为多少时，该窗的透光面积最大（精确到0.1 m，且不计铝合金型材的宽度）？

用较少的材料制作透光面积尽可能大的窗框，是生活中常见的优化问题之一，也是利用二次函数探究与几何图形有关的最大值问题.本题如果直接抛给学生，不易解答.笔者在讲解这道题目时采用了化零为整、由易到难的方法，通过一组有梯度的问题，既降低了难度，又让不同层次的学生都有回答的机会，又让学生对已掌握的知识进行梳理分析，透过问题看清本质.

师：用20米的铝合金型材围成一个矩形窗框，如图，有几种制作方法？什么时候面积最大？

生1：无数种，围成正方形面积最大.

师：现在要在中间加一根铝合金EF，设AB=x，则AD等于多少？

生2：AB=20-3x2.

师：当x为多少时，这个窗框是一个正方形？

生2：x=20-3x2，x=4.

师：你们也是這么做的吗？

生3：20÷5=4，边长为4.

师：好方法，不用解方程，直接求得边长.此时面积是多少？

生3：16.

师：当AD为多长时，窗框的面积是16 m2？

生4：4

生5：可能还有一个答案.

师：请你试试

生5：x·20-3x2=16，解得x1=4，x2=83.当AD为4或83时，窗框的面积是16 m2

师：窗框的面积能达到17 m2吗？如何列方程？

众生：x·20-3x2=17

师：你有什么想法？

生6：不可能是17.

师：为什么？

生6：因为正方形时面积最大.

师：超过16不可能吗？

生7：可能.因为中间有一条.

師：正是由于中间加了这条导致并不是正方形时面积最大，来试试17有没有可能.化简后得3x2-20x+34=0，b2-4ac0，方程没有实数根.还有其他解法吗？

众生：（沉默）

师：16.9，16.8，16.7？有方法吗？

生8：可以求最大值

师：非常好！请同学们动笔来算一下

学生很快得到x·20-3x2=-32x2+10x=-32x-1032+503，最大值为503.

四、层次清晰

数学学习具有高度的抽象性，初中生虽已形成了形式运演思维，具有一定的抽象思维能力，但面对新知识的学习、陌生的任务，他们常常还是要借助具体事物的支撑.所以教师设计的问题要有层次性，应该体现思维发展的要求，教师要紧扣教材的重点难点，分析教材内容的内在联系、逻辑顺序，按照由具体到抽象，由已知到未知，由感性到理性的认知规律，由易到难，由简到繁，循序渐进的设计问题，是学生的认识逐渐深入，提高.

再次学生是学习的主体，由于智力发展水平及个性特征的差异，不同的学生对同一事物的理解角度和深度必然有明显的差异.有很多教师偏向于设置有一定难度的问题，常提问成绩较好的学生，这样学习能力弱的学生就会感受到被冷落，久而久之，就会失去学习的兴趣与信心.因此，在课堂教学中，教师必须考虑学生的差异性，在问题设计方面要考虑学生水平的层次性，对不同程度、不同学习能力的学生提出不同的问题，这样既能符合学生的思维特点，又能让每一个学生都能有机会参与到课堂学习中.

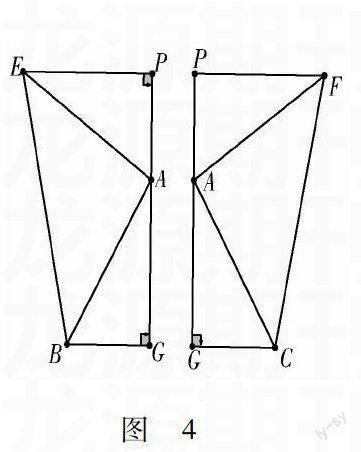
如图1，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E，F作射线GA的垂线，垂足分别为P，Q. 试探究EP与FQ之间的数量关系，并证明你的结论.

问题1：这个图形中有你熟悉的几何图形吗？

分析：这个问题比较基础，而且是一个开放性的问题，可以让第四类学生（理解能力弱、被动回答）来回答，学生很容易找到Rt△APE、Rt△AGB 、Rt△AGC 、Rt△AQF、等腰直角三角形EAB，等腰直角三角形FAC.

问题2：这些图形之间有什么关系吗？（学生容易考虑到三角形全等，但是由于此图形较复杂，不容易找出其中的对应关系.此时可出示问题3进行过渡）

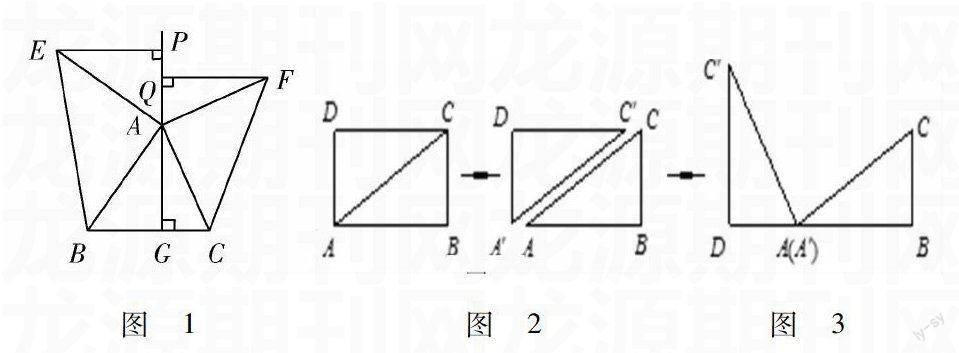
问题3：将矩形ABCD纸片沿对角线AC剪开，得到△ABC和△A′C′D，则△ABC和△A′C′D之间的关系式.如图1所示.将△A′C′D的顶点A′与点A重合，并绕点A按逆时针方向旋转，使点D、A（A′）、B在同一条直线上，如图2所示.观察图2可知：与BC相等的线段是，∠CAC′=°.

图 4分析 学生容易理解，容易解决，为后面的探究做好铺垫，学生发现找一个与EP和FQ都相等的线段也就是划归为问题3中的基本图形“蝴蝶型”全等.将图4分解为两个基本图形，分别得Rt△ABG≌Rt△EAP，得出EP=AG.同样Rt△ACG≌Rt△FAQ，得出FQ=AG.从而得证EP=FG.

五、激趣启发

王梓坤院士曾指出：“数学教师的职责之一就在于培养学生对数学的兴趣，这等于给了他们长久钻研数学的动力，优秀的数学教师之所以在学生心中永志不忘，就是由于他点燃了学生心中热爱数学的熊熊火焰”

兴趣在教学中起着决定性的作用.教师设置的提问可以来源于生活，也可以来自数学本身或其他学科，要通过问题呈现刺激性的信息，激发学生的学习兴趣，引发认知冲突，诱发质疑猜想，调动生学习的积极性、主动性.而在此过程中，教师只须因势利导，巧妙点拨，可以很好地完成教学任务，而且会取得出人意料的教学效果.

在不等式教学中，我们常感到很抽象.例如：ab

六、开放创新

低效率的数学课堂上教师抛出的问题数量不少，但是其中封闭性问题占大部分，开放性问题较少.若能设置适当的开放性的问题，一方面可以满足不同水平学生能力的差异，另一方面可以使学生对数学多方位、多角度去联想、思考、探索，有利于拓展学生思维的深度和广度，培养学生的创新能力.

如在学习平行四边形的判定时，有这样一道题目：在四边形ABCD中，AD∥BC，对角线AC与BD相交于点O，请添加一个条件，使四边形ABCD成为平行四边形.这是一道开放题，放在平行四边形的判定的复习课上，能较好地复习判定方法，但在平时新课教学中，难度会太大.因此，这需要老师改编题目，让题目的难度适合学生，比如可以加上：（1）添加条件后，可用“两组对边分别平行的四边形是平行四边形”来判断.（2）添加条件后，可用“一组对边平行且相等的四边形是平行四边形”来判断.根据学生的具体情况，也可以有其他的改编形式.

【参考文献】

[1]王梓坤.让你开窍的数学[M].郑州：河南科学技术出版社.1997.2.第46页.

[2]罗增儒.中学数学课例分析[M]. 西安：陕西师范大学出版社.2001.2.第205页.