基于GARCH模型的VaR方法在商业银行利率风险度量的应用
作者简介:孙祥康(1990.12-),男,汉,山东省青岛即墨市,硕士在读,吉林财经大学,研究方向:数量经济学。
摘要:随着经济不断发展,制度、监管的不断完善,管制利率体质下的金融市场难以满足国际接轨的需求,我国金融自由化不断深化。虽然现阶段我国仍处于利率管制向利率市场化过渡的时期,但银行同业拆借利率、债券利率和外币利率作为金融市场导向利率基本已经实现了市场化改革,利率市场化程度愈加深化。文章采用VaR模型和GARCH模型,以shibor同业拆借利率和利率敏感性缺口计算商业银行的利率风险。
关键词:GARCH模型;VaR模型;利率风险
一、选题背景及意义
随着金融市场的不断完善,我国金融自由化程度不断加深,利率制度逐步由管制利率制度向利率市场化过渡,人民银行允许金融机构人民币存款利率在允许的范围内上下浮动,银行同业拆借利率、债券利率和外币利率作为金融市场导向利率基本已经实现了市场化改革,利率市场化程度愈加深化,利率的变动会直接影响商业银行的日常经营。在以上的背景下,本文以适当的方法量化银行的利率风险,对银行规避利率风险具有借鉴意义。
随着金融理论和衍生金融工具的不断创新,商业银行面临的市场风险和内部风险的相关性、复杂性也不断增加。风险价值法(VaR方法)由于能够全面量化复杂投资组合的市场风险,为人们所广泛应用。VaR(Value at Risk)表示在给定的置信区间内,市场正常波动状况下,资产组合可能的最大损失。而ARCH族模型在处理金融时间序列数据方面显示出强大的优越性,可以与VaR参数相结合来处理金融市场数据。因此我们最终选择基于ARCH族模型的VaR方法。
二、风险价值分析方法和ARCH模型介绍
风险价值分析(Value at Risk,简称VaR)是指在正常市场波动情况下,某一金融资产或投资组合在给定的置信水平下,在未来特定的一段时间内(一天、一周或十天)可能发生的最大损失,可以表示为:
prob(Δp>VaR)=1-α
其中,prob表示金融资产或投资组合在将来特定的一段时间内损失超过可能遭受的最大损失(VaR)的概率,Δp表示在持有期内金融资产或投资组合的可能损失值,α表示置信水平。
假设我们知道投资组合的收益概率分布,经计算(推倒过程见约翰.赫尔. 风险管理与金融机构[M].中信出版社,2009)投资组合的VaR值可做如下表示:
VaRr=-V0ZασΔt
式中,V0表示金融资产或投资组合的初始值,Zα为相应的置信水平所对应的分位数,α为置信水平,Δt为持有期,σ表示投资组合的波动性。因为我们分析商业银行的利率风险,所以V0我们用利率敏感性缺口度量,σ表示投资组合的波动性,我们用shibor银行间同业拆借利率拟合的ARCH(GARCH)模型的条件方差衡量。
Engel(1982)指出,如果序列{εt}的方差不恒定,就可以用ARMA模型来估计方差持续变动的趋势,将残差的估计值的平方条件方差建模为AR(P)过程:
ε∧2t=α0+α1ε∧2t-1+α2ε∧2t-2+…+αpε∧2t-p+υt
式中vt为白噪声过程。我们将上式表示的模型称为自回归条件异方差(ARCH)模型。
Bollerslev(1986)在Engel的原始模型的基础上,将原模型的条件异方差转化为一个ARMA过程的方法。现在假定误差过程为εt=υtht,其中,σ2υ=1,且ht=α0+∑qt=1αiε2t-i+∑pi=1βiht-i。
我们把上面的式子称为GARCH(p,q)模型。
三、 实证分析
我们选取2011.12.5—2014.12.4 shibor同业拆借利率的隔夜利率进行分析:
(一)平稳性检验
我们用到的单位根检验的模型为:
Δyt=γyt-1+∑pi=1βiΔyt-i+1+εt
在此模型中,原假设H0:时间序列存在一个单位根,备择假设H1:时间序列平稳,不存在单位根;如果检验结果拒绝H1,则说明时间序列存在一个单位根,为非平稳时间序列。
根据结果我们可以看出,ADF检验的T统计量为4.5699,P值为0.1018>0.05,因此我们认为原序列存在单位根。
下面,我们对原始数据进行一阶差分。我们对差分后的数据进行单位根检验得出结论差分后的数据ADF检验在1%,5%,10%的显著性水平下其T统计量的P值均支持接受无单位跟的假设。一阶差分后数据平稳。
(二)正态性检验
我们已经得到一阶差分后的平稳数据,对数据进行正态性检验。对时间序列做Jarque-Bera检验,统计量公式如下:
JB=(N-k)/6(S2+1/4(K-3)2)
其中,S表示偏度(SkewnesS),K表示峰度(Kurtosis),N为样本个数,k为待估方程中的参数个数。如果数据呈标准正态分布,偏度S=0峰度K=3。Jarque-Bera检验的原假设H0:序列的分布与正态分布无显著性差异,备择假设H1:序列的分布与正态分布有显著性差异。由分析得知,数据的偏度S=3.56较正态分布(S=0)右偏。峰度K=26.93,较正太分布(K=3)陡峭。而JB统计量的P值为零,我们拒绝数据呈正态分布的原假设。鉴于这种“尖峰厚尾”数据,在接下来的估计中我们采用广义误差(generalized error distribution)GED分布。
(三)自相关性检验
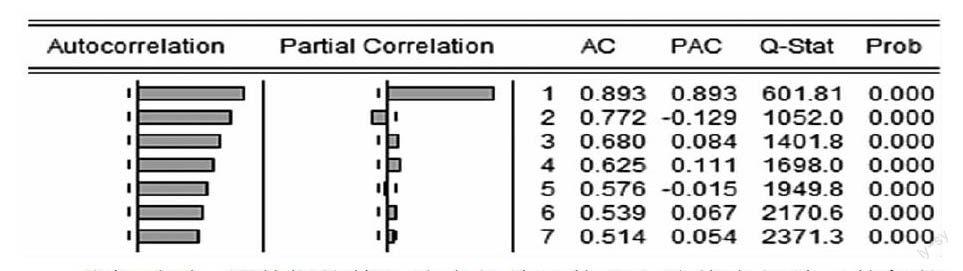
我们通常用到的为数据的自相关图,偏自相关图,差分数据的自相关图,偏自相关图。
我们看到,原数据的前7阶自相关系数和1阶偏自相关系数都较大,且Q统计量较大。说明存在自相,差分后的一阶数据Q统计量的P值大于0.05,我们认为存在一阶自相关。
(四)ARCH效应检验
前面我们已经验证数据存在一阶自相关,下面我们拟AR(1)方程,并对残差进行ARCH-LM检验。我们构造的均值方程为:
logrt=βlogrt-1+εt
其中logrt-1为原序列取对数滞后1期的时间序列,εt为序列残差,用普通最小二乘法(ls)对均值方程做自回归估计:
logrt=0.996logrt-1
t311.91
经过计算分析可以得出,参数的T统计量的P值都为零,参数显著,模型的R2为0.873,调整后R2为0.873,可以认为模型拟合较好。
下面我们进行残差平方的自相关性检验。 经过验证分析可以得出,残差平方的一阶自相关系数和偏自相关系数小比较而言较大,且Q统计量较大,P值为零,说明原时间序列中存在ARCH效应,即拆借利率时间序列中存在异方差现象。
ARCH-LM检验显示,常数项和滞后一期的残差平方项的系数T检验显著不为零,总体F值为191.138,F统计量的P值为0。因此存在ARCH效应。
通过以上对原时间序列的检验,我们得出结论:1、原时间序列存在单位跟,为非平稳时间序列,经过对数一阶差分后的时间序列相对平稳;2、原数据时间序列与正态分布存在显著差异,存在厚尾现象;3、时间序列存在很强的自相关性,对原序列取对数进行一阶差分后自相关现象仍存在,但相对较弱;4、ARCH-LM检验结果认为时间序列中存在异方差现象,而且存在ARCH效应。
前面已经得出数据的对数一阶差分呈一阶自相关,所以我们用残差服从GED分布的GARCH(1,1)模型进行拟合。我们在拟合GARCH模型是均值方程和条件方差方程分别为:
logrt=βlogrt-1+εtht=a+bε2t-1+cht-1
进过计算分析,我们可得知均值方程中自相关项系数的Z统计量的P值都为零,系数显著。方差方程中残差平方项和GARCH项的系数的Z统计量的为零,因此系数显著。
下面我们通过ARCH-LM检验,进一步检验模型是否存在时间序列的ARCH效应,确保新生成的时间序列不存在ARCH效应。
经计算分析可得出检验结果,从检验结果分析可知,WGT_RESID^2(-1) 、WGT_RESID^2(-2) 、WGT_RESID^2(-3)、 WGT_RESID^2(-1)的P值均大于005,不显著,因此可以得出新生成的序列的ARCH效应己经消除掉。
我们通过ARCH-LM检验,消除“条件方差”序列的ARCH效应,然后用新生成的“条件方差序列”的平方根除以消除自相关现象的拆借利率时间序列 (此序列中含有ARCH效应),进而生成消除ARCH效应的新时间序列。
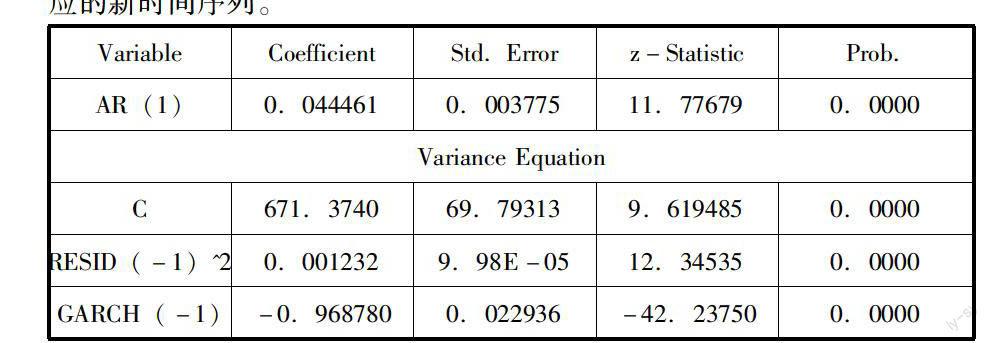
VariableCoefficientStd. Errorz-StatisticProb.
AR(1)0.0444610.00377511.776790.0000
Variance Equation
C671.374069.793139.6194850.0000
RESID(-1)^20.0012329.98E-0512.345350.0000
GARCH(-1)-0.9687800.022936-42.237500.0000
得到我们最终拟合的GARCH(1,1)方程为:
DLrt=0.4446DLrt-1+εt
Z11.777
ht=671.3740+0.0012ε2t-1-0.9688ht-1
Z9.61912.345-42.238
(五)VaR计算
前面我们已经说明:VaRr=-V0GασΔt
V0我们用银行利率敏感性缺口衡量;因为我们在GARCH模型的估计中选择残差服从GED分布,所以Gα我们选择95%的置信度形状参数V=1.5的GED的分布限;我们选择的shibor隔夜同业拆借利率,所以我们令Δt=1;σ则用我们估计的GARCH(1,1)模型的条件方差表示。鉴于我们选择的样本数据的时间为2011.12.5—2014.12.4,所以V0我们选择2010年商业银行的利率敏感性缺口。
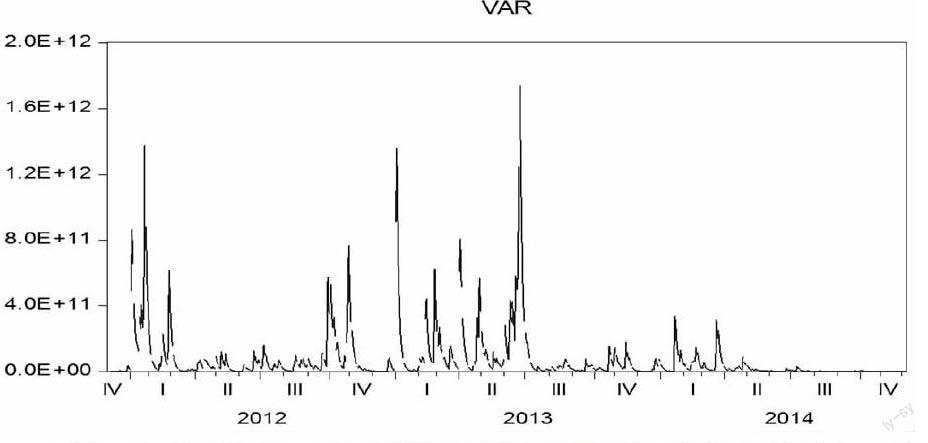
我们得到利率敏感总缺口为-2302743百万。我们得到VaR线图:
图中,E代表万亿。我们可以看到我国商业银行的VaR值较大,且数据波动较大。大部分时间,银行的VaR分布在4.0万亿以下,但在有的日期波动较大,VaR值达到8万亿甚至更高,而这意味着,虽然有很小的概率(我们一般取5%或1%),但利率波动给商业银行带来的损失可能超过商业银行的资产。由此可见,利率波动可能给商业银行带来巨大的损失。商业银行必须谨慎管理利率敏感性缺口,合理调整资产负债表的期限结构,处理好资金流动性、安全性、盈利性之间的关系;其次,商业银行应该加速转型,大力发展服务业,减小主营业务收入在总收入中所占比重,以减少暴露在利率风险中的资产规模,减小利率风险。
现阶段,我国加速推进金融自由化,利率市场化改革愈加深化,虽然央行可以在一定程度上调整利率,但利率波动受市场的影响越来越大。从表中各商业银行较大利率敏感性缺口可以看出,商业银行对利率风险没有给予较大重视,加上我国正处在从管制利率体制向浮动利率体制过渡阶段,利率风险管理及度量的理论、人才缺乏,信用评级制度体系建设落后,监管的法律、制度不完善使得商业银行在管理利率风险方面困难重重。(作者单位:吉林财经大学)
参考文献:
[1]徐永强. 基于GARCH的VAR方法的商业银行利率风险度量研究[D]哈尔滨:哈尔滨工程大学,2011
[2]赵鹏. 基于GARCH模型的VaR方法的实证研究[D]山东:山东大学,2013
[3]Walter Enders.Applied Econometric Time Series[M]杜江,袁景安译.北京:机械工业出版社,2012.6
[4]约翰.赫尔. 风险管理与金融机构[M].北京:中信出版社,2009

