四色猜想（定理）简单证明

王锦根

【摘要】通过相邻关系存在区域多少，证明四色猜想成立.

【关键词】四色猜想；图论

一、概念

地图四色定理（Fourcolortheorem）最先是由一位叫古德里FrancisGuthrie的英国大学生提出来的.四色问题的内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色.”用数学语言表示即“将平面任意地细分为不相重叠的区域，每一个区域总可以用1234这四个数字之一来标记而不会使相邻的两个区域得到相同的数字.”这里所指的相邻区域是指有一整段边界是公共的.如果两个区域只相遇于一点或有限多点就不叫相邻的.也就是说在不引起混淆的情况下一张地图只需四种颜色来标记就行

区域颜色

A色1

B色2

C色3

D色4

…………

二、初探及证明

在平面或地图中，至少需要几种颜色（简称“几色”）标注具有共同边界的区域或国家.如果数个区域任意两个均不相邻，则依旧可用单色（一色）标识，如在地图中，我们任选一种颜色，当我们将其他颜色抹去后，将会发现它们互不相邻.所以，相互相邻的区域多少，决定了颜色的多少.我们可以从最少数量拓展.

定理1在平面中，相互相邻区域的多少，决定了颜色的多少.

性质1数个互不相邻的区域，可以采用单色标记.

注：A，B，C，D，…，表示区域名称，此时A，B，C，D可以同色.

性质2如果两个区域相邻，则可以两色标记.

性质3如果三个区域相互相邻（即任两个区域相邻），则可以用三色标记.

由于A，B，C三个区域相互相邻，则A，B，C三个区域按照平面上的点来计，则形成封闭的三角形，那么第4块区域怎么与A，B，C相邻呢？

设第四块区域D.

1.如果D不能同时与A，B，C相邻，则色数不增加.假如D不能与C相邻，则D，C可采用同一色.

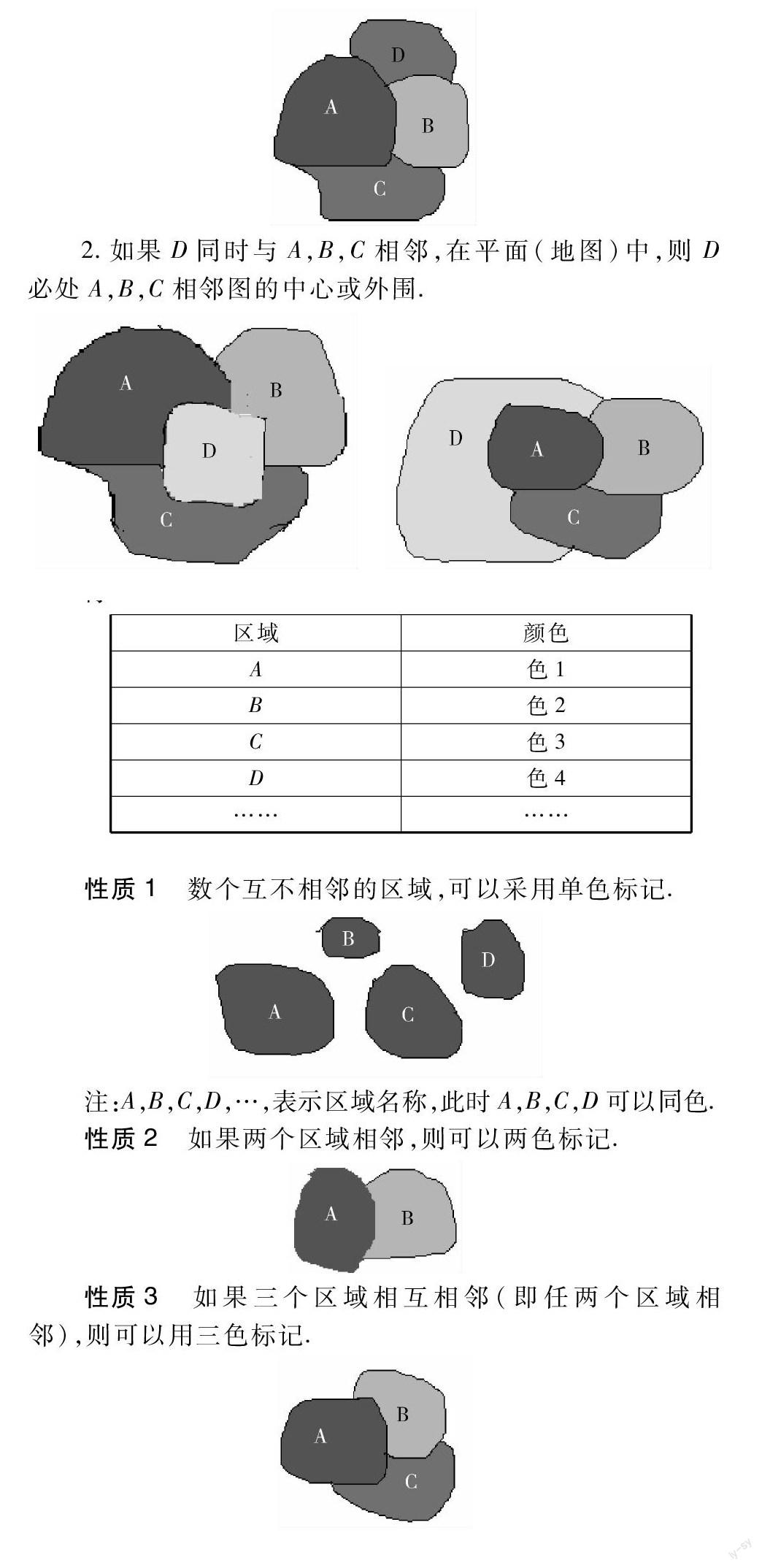
2.如果D同时与A，B，C相邻，在平面（地图）中，则D必处A，B，C相邻图的中心或外围.

（1）当D处于A，B，C相邻中心时，则D被A，B，C包围（与外界隔离），似乎增加D区域，标记为色4，但A，B，C，D区域外的区域仍可以利用色4标记，色4成了其他（向外扩展）区域的机动色（即：可以再次使用或标记），无需增加色5.形象地说，当一色被隔离（“死亡”）后，它可以在随后的其他地方“复活”.四色定理从这点理解应该是“3+1”色，这个“1”表示为可再次使用的颜色，即在四色中，向外拓展时，有一种颜色可以再次使用，那就是这个“1”色.

（2）当D与相邻的A，B，C外围相邻时，虽然用色4标记，这是至少有一色被D區域“与世隔绝”，当E区域标记时，被隔离的一色可以与区域E同色.同样，四色定理可以理解为“3+1”定理，无需增加色5.

定理2在平面中，相互相邻区域的最多为4.

所以在地图（平面图）颜色标记中，当三个区域相邻时，每增加1个区域（颜色）与三个区域相邻时，虽然增加1个颜色，达到四色，但同时必有“1”或以上被“隔离”而被再次使用，“3+‘1-1+1-……”如此循环不断下去，始终不会超过四种颜色.

综上所证，在平面或地图中，各区域颜色标记可以用“3+‘1-1+1…”或“3+1”颜色标记，即四色猜想（定理）成立.

【参考文献】

[1]张文忠.数园撷英[J].科学普及出版社，1983.