职业教育中专业课程设置的可行性研究

赵东升??杨臻??徐春玲

【摘要】本文应用现代课程论观点和原理，从系统和整体优化的角度出发，对职业教育中专业课程设置能力需求、课程需求与重要性、课程内容相关需求、课程相对知识量等方面进行定性与定量相结合的分析，从而确定专业课程设置与否，确定教学量和考核方式。

【关键词】课程 设置 需求 分析

【中图分类号】G712.3 【文献标识码】A 【文章编号】2095-3089（2015）19-0103-02

1 引言

近年来，随着职业教育改革的不断深化，各类职业院校的专业课程体系改革和建设也在探索适应社会发展和市场经济体制的途径。越来越注重素质教育；重视学生创新能力的培养和个性发展。因此，各专业主要专业课程设置的确定，应改变传统的由各学科专家根据培养目标、教学任务、教学规律和教育资源条件，结合各自的教学经验，经过反复平衡、多次协商而确定的做法。本文用现代课程论观点和原理，围绕教育目标，从系统和整体优化的角度出发，集中各类专家的经验，对课程设置的可行性进行能力需求、课程需求、课程内容相关需求、课程相对知识量等方面进行定性与定量相结合的分析，从而使各专业主要专业课程设置更适应社会经济发展需求，具有实用性、操作性和科学性。

2 能力需求分析

能力本身是一个比较抽象的概念，它主要指培养的各类专业人才，在适应社会需求中调节已经具备的专业知识、技能的概括性心理活动的具体体现。但不同类型的职业院校，不同的专业根据培养目标和教学大纲，经社会、职业的需求分析，对能力或素质均有要求标准。这些要求标准就构成了能力向量。设有n种能力分量，第j种能力分量需求度记为Aj，则其能力需求向量为：A=（Aj| j=1、2、……，n）。根据能力向量的各个分量，利用德尔菲法邀请行业部门专家定性确定对各种能力分量的需求。并应用模糊数学原理，赋予不同等级需求能力分量相应数值，参照表1，专家们定量确定各个能力分量的需求度。

设有K名专家进行论证和预测，第R（R=1，2，……K）位专家对第j种能力分量的评分等级的对应值为aRj，则第j个能力分量综合评分均值为：

（1）

3 课程需求与重要性分析

根据能力需求分析确定的各种能力分量，必须设置与之相关的主要专业课程，以保证各种能力的培养目标的实现。这些设置的课程组成了课程向量，它们可由院校有经验的专家遵循教学规律确定。设有m门课程分量，第i门课程分量需求度记为Bi，则课程需求向量为：B=（Bi│i=1，2，3，……，m）。根据能力向量的各个分量，确定对每一个课程分量的需求度。设第j个能力分量Aj对第i门课程分量Bi的需求度为bji。其数值可由院校有经验的专家参照表1评分确定。若有P位专家进行评分，第Q（Q=1，2，……，P）位专家对第j个能力分量Aj所对应的第i门课程分量Bi的需求度评分为bQji，则P位专家综合评分的均值为：

（2）

由此可得，能力与课程矩阵（bji）n×m。则课程向量B为：

B={B1，B2，…Bm}=（A1，A2，…An）（bji）n×m（3）

向量B集中了行业部门和院校两部分专家对各门课程需求度的描述，向量B中必有分量Bj=max（B1，B2，…Bm），则Bj这门课程相对其它课程更为重要，因此可以依次列出m门课程相对需要序列。

例如：某职业院校在计算机科学与技术专业的课程设置中，在IT行业邀请了5位专家对该专业培养的学生能力需求进行定性与定量论证，专家们根据IT行业现状与发展的实际，一致认为该专业培养的学生应具有A1={操作计算机能力}；A2={开发和利用计算机软件的能力}；A3={排除计算机设备简单故障能力}；A4={计算机系统分析和设计能力}。并参照表1分别给出各种能力需求值如表2：

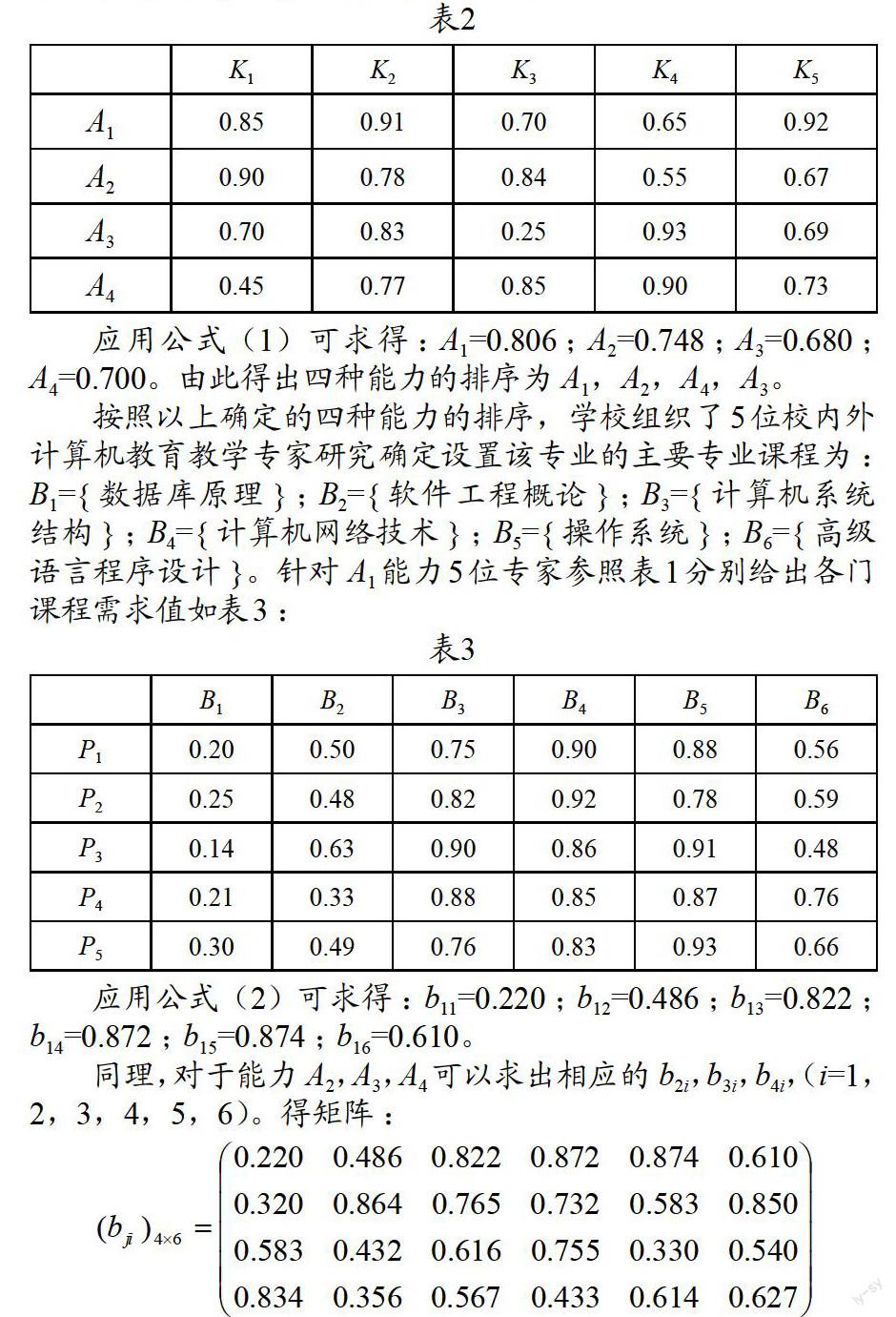
应用公式（1）可求得：A1=0.806；A2=0.748；A3=0.680；A4=0.700。由此得出四种能力的排序为A1，A2，A4，A3。

按照以上确定的四种能力的排序，学校组织了5位校内外计算机教育教学专家研究确定设置该专业的主要专业课程为：B1={数据库原理}；B2={软件工程概论}；B3={计算机系统结构}；B4={计算机网络技术}；B5={操作系统}；B6={高级语言程序设计}。针对A1能力5位专家参照表1分别给出各门课程需求值如表3：

应用公式（2）可求得：b11=0.220；b12=0.486；b13=0.822；b14=0.872；b15=0.874；b16=0.610。

同理，对于能力A2，A3，A4可以求出相应的b2i，b3i，b4i，（i=1，2，3，4，5，6）。得矩阵：

应用公式（3）可求得：B=（1.40，1.58，2.05，2.07，1.79，1.93）。由此得出六门计算机科学与技术专业的主要专业课程的排序为B4，B3，B6，B5，B2，B1。

4 课程内容相关性分析

课程内容相关是指各课程内容内在的相关程度，它是第i门课程必须为第j门课程向学生输送相关知识的程度。因此需将讲授的课程内容划分为若干个基础知识，即学习这门课程所需的知识，称为存储知识；以及要学习的新内容，称为新知识。在此基础上确定课程之间的相关程度。

设讲授的课程内容Z共分为m个周期（划自然章、节），由E种（或门）基础知识构成，记作t=（t1，t2，…tE）用qj=（t1j，t2j，…tEj）表示第j周期新知识与存储知识的相关程度，其中不相关的为零。

qj的计算，建立基础知识相关程度的两两比较正互反矩阵M=（mij）E×E，使用Saaty提出的1—9两两比较尺度，mij的取值范围是1，2，…，9及其互反数1，1/2，…，1/9。mij的确定是以的基础知识ti与tj相关程度的比值，该比值主要根据教师的教学经验及对教学内容分析研究而确定。正互反矩阵M具有（i，j，k=1，2，…，E），即正互反矩阵A为一致性矩阵。

由矩阵Perron—Frobineus理论，应用特征根法计算M中各元素的相关程度。

Mqj=λmaxqj（4）

其中λmax为最大特征根，规一化qj=（t1j，t2j，…，tEj）且。为第j周期新知识与存储知识的相关程度。

例如：数理统计学中抽样分布一章，基础知识由高等数学、概率、抽样分布组成，其中抽样分布为新知识。两两比较的判断矩阵M为

相应的主特征根与特征向量分别为λmax=3.02，ω=（0.35，0.45，0.2）。由此得数理统计学中抽样分布一章新知识与高等数学、概率两门课程的相关程度为0.35，0.45。

5 课程相对知识量分析

课程相对知识量是指该门课程的新知识与存储知识之比。记为θ。设：

5.1 课程的知识由E种（或门）基础知识（包括存储知识和新知识）构成。记作t=（t1，t2，tE）；

5.2 这E种（或门）基础知识分别归属于m个周期（或自然章、节）；

5.3 各周期在该门课程中的权重为C=（C1，C2，…，Cm）；

5.4 第j周期各基础知识的权重为dj=（dj1，dj2，…，djE），其中j周期中没有的基础知识为零。建立基础知识相对知识量的两两比较正互反矩阵G=（gij）E×E，由矩阵Perron—Frobineus理论，应用特征根法计算出第j周期各基础知识的权重dj=（dj1，dj2，…，djE），令D=（d1，d2，…，dm）T。该门课程各基础知识权重记为e，则：

e=（e1，e2，…，eE）=C1xm·DmxE（5）

将e规一化处理后，各基础知识权重为e′=（e′1，e′2，…，e′E），若e′中有k

e1″，e2″，…，ek″。则该课程的相对知识量为：

（6）

6 课程掌握度分析

课程掌握度是对学生提出的课程要求掌握程度，其数值可由院校有经验的教育专家参照表2评分确定。

设有H名专家参与评分，第h位（h=1，2，…，H）专家对第i门课程评分为hi，则H名专家对第i门课程评分的评分均值为：

（7）

si即为第i门课程的掌握度。

7 结束语

综合上述，由能力需求分析、课程需求与重要性分析确定课程的设置与否；由课程内容相关需求分析、课程相对知识量分析确定课时量；由课程掌握度分析确定课程的考核方式。

参考文献：

[1]查有梁著.教育建模（第二版）[M].广西：广西教育出版社，2001，65

[2]于淑云，李诚忠主编.教育系统工程[M].吉林：东北师范大学出版社，1995，87

[3]查有梁著.控制论、信息论、系统论与教育科学[M].四川：四川省社会科学院出版社，1986，135