不确定非线性时滞系统的同时 保代价控制
张佳玲 包俊东

【摘要】本文所考虑的问题是设计一个静态输出反馈控制器,来同时二次镇定一族不确定非线性时滞系统,使得闭环系统满足一定的H∞性能要求且具有保代价。文章给出了公共反馈增益矩阵存在的一个充分条件,并且通过解一组线性矩阵不等式求得了这一反馈增益矩阵,同时可解出系统族的一个公共Lyapunov-Krasovskii泛函,进而求得系统族的保代价。文中实例验证了本文方法的有效性。
【关键词】不确定非线性时滞系统 同时H∞控制 保代价控制 线性矩阵不等式
【基金项目】 内蒙古师范大学十百千人才项目;内蒙古师范大学2014年度研究生科研创新基金项目(CXJJS14054)。
【中图分类号】TP13 【文献标识码】A 【文章编号】2095-3089(2015)19-0254-02
1 引言
控制系统的同时镇定问题于1982年由Saeks和Murray以及Vidyasagar和Viswanadham首先提出。其后,很多学者这一问题进行了研究并在此基础上考虑系统的H∞性能表现,得到了很多有价值的结论。为了降低结论的保守性,Chang等人于1972年在自适应控制中提出了保代价控制的概念。这一方法是在解决以上鲁棒缺陷方面起到了非常重要的作用,因此得到了很大的发展。
本文所考虑的是不确定非线性时滞系统的同时H∞保代价控制问题。通过设计一个静态输出反馈控制器来使得闭环系统族同时二次稳定,且具有H∞性能以及保代价。文章通过解一组线性矩阵不等式求得了这一公共反馈增益矩阵,同时可解出系统族的一个公共Lyapunov-Krasovskii泛函,进而求得系统族的一个保代价,实现了系统族的同时H∞保代价控制。
2 问题描述
考虑以下系统族:
i=1,2,…,s
其中想x(t)∈Rn是系统状态变量;u(t)∈RP是系统控制输入;ω(t)∈Rq是系统干扰输入;z(t)∈Rm和y(t) ∈R1分别表示系统控制输出和系统量测输出;τ>0 是系统状态时滞;Ai∈Rn×n,Ai∈Rn×n ,Bi1∈Rn×p, Bi2∈Rn×q,Ci1∈Rm×n,Ci∈R1×n ,D1∈Rm×q是系统矩阵,△Ai,△∧i,△Bi1为不确定矩阵,且 具有形式[△Ai △∧i △Bi1]=GE[Hia Hid Hib].其中,G,Hia,Hid,Hib为适当维数的实矩阵,E为未知的时变矩阵,且满足ETE≤I.
这里假设不确定非线性项fi满足 ,i=1,2,…,s.
其中
取性能指标函数:
(2)
其中S>0,R>0为加权矩阵.
采用输出反馈u=Ky(t),则相应的闭环系统为:
其中
性能指标函数为:
i=1,2,…,s (4)
引理1:对于任意适当维数的向量x,y和实值矩阵D,E,对于任意适当维数的矩阵F,如果F满足FTF≤I,那么以下不等式成立 这里ε>0是任意常数。
引理2:若 是对称矩阵,那么以下三个条件等价
Ⅰ) W<0;Ⅱ) W1<0,W3-W2TW1-1W2<0;Ⅲ) W3<0,W1-W2W3-1W2T<0.
3 主要结果
定理:如果存在正定对称矩阵P和Q使得以下矩阵不等式组存在公共可行解K
i=1,2,…,s. (5)
那么通过静态输出反馈控制器u=Ky(t),对于所有允许的不确定性,闭环系统族满足
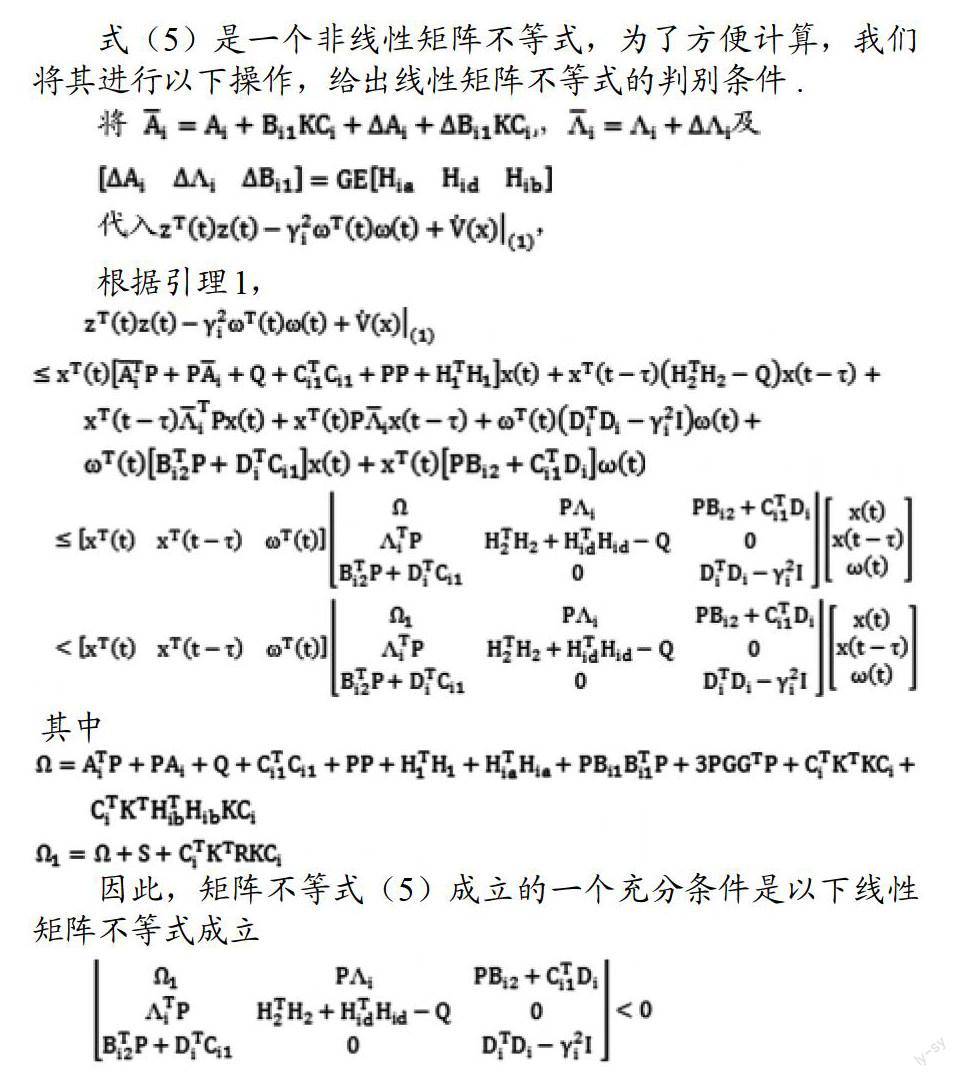
Ⅰ) 同时二次稳定;Ⅱ) 对于给定γi>0,假定初始条件x(0)=0,则||z(t)|| ∞<γi||ω(t)|| ∞,对于任意T>0及任意ωi(·)L2[0,T]成立,i=1,2,…,s ;Ⅲ) 代价函数(2)的闭环值满足Ji 证明: ω(t)=0时系统的二次稳定性 选取Lyapunov-Krasovskii泛函 i=1,2,…,s. (6) 其中P和Q是(5)式中的正定对称矩阵,显然V(0)=0并且Vi(φ)>0, φ≠0. 由于 由(5)式知i(x)|(1)<0,因此系统族同时二次稳定. 2)存在保代价J*使得Ji 由(5)式知 则有 因此 取 ,则J*为系统族的一个保代价. 3)系统的H∞性能 式(5)是一个非线性矩阵不等式,为了方便计算,我们将其进行以下操作,给出线性矩阵不等式的判别条件. 根据引理1, 其中 因此,矩阵不等式(5)成立的一个充分条件是以下线性矩阵不等式成立 4 结论 本文考虑了不确定非线性时滞系统的同时H∞保代价控制问题。通过解一组线性矩阵不等式,得到了公共反馈增益矩阵,以及系统族的一个公共Lyapunov-Krasovskii泛函。进而通过静态输出反馈,实现了系统族的同时H∞保代价控制。本文所研究的问题可以通过状态反馈来实现,也可以设计动态输出反馈控制器来达到与本文同样的目的。 参考文献: [1]Saeks R, Murray J, Fractional representation, algebraic geometry and simultaneous stabilization problem [J].IEEE Trans. Automatic Control, Vol.27, No.5, 895-903, 1982 [2]Vidyasagar M. Viswanadham N. Algebraic design techniques for reliable stabilization [J]. IEEE Trans. Automatic Control. Vol.27, No.5, 1085-1095, 1982 [3]Saif A, Gu D, Kavranoglu D, el al. Simultaneous stabilization of MIMO systems via robustly stabilizaing a central plant [J]. IEEE Trans. Automatic Control, Vol.47, No.2, 363-369, 2002 [4]Miller D E, Rossi M. Simultaneous stabilization with near optimal LOR performance [J]. IEEE Trans. Automatic Control, Vol.46, No.10, 1543-1555, 2001 作者简介: 张佳玲,女,汉族,1990年出生于内蒙古赤峰市,目前为内蒙古师范大学在读硕士研究生。

