数形结合方法在高中数学教学中的应用研究

张荣荣

【摘要】二十一世纪，高等教育的难度不断加深.为了快速有效地提高学生的成绩，必须进行教学方法的优化.其中，数形结合的方法是提高学生学习效率的有效途径之一.本文论述了数形结合方法在高中教学中的具体应用及其作用.

【关键词】数形结合；学习效率；高等教育

数学是高中教育中重要的学科，对学生思维的逻辑性要求较高，因此总体上是门偏难的科目，大多数高中生成绩不理想皆与数学有关.因此，提高学生的数学知识接受率迫在眉睫.而在高中数学中，数形结合无论是对于教学者还是学习者，均是个不错的选择.这种方法能将抽象的数学问题具象化、简单化，从而激发学生的学习兴趣.

一、数形结合方法的应用原则

1.数形结合的含义

数学研究包含两类基本对象，即“数”与“形”，它们彼此独立又相互联系.形是数的具体表现，而数则是形的一种概括.而数形结合，则是将数量问题转化为图形问题，或者逆向思维将图形问题转化为数量问题，从而获取更为简洁的思考方法.简而言之，就是将直观的图像和较为抽象的数学语言相结合.

2.应用数形结合方法的原则

首先，最基本的要遵循简洁性的原则.构图必须简洁明了，这样才能让学生一目了然激起探讨兴趣，若图形比原有数字还要复杂，教学效果可想而知.其次，要遵循等价性原则.如果构建的图形与原有代数式子不符，在数学运算中，一点点的偏差都可能得出天壤之别的结果.这种没有遵循等价性的数形结合，其运算结果只能适得其反.其三，要把握双向性原则，因为数形结合方法是数与形的互补，是理论知识的图像具象化，在将“数”转化为“形”后，更要检测当反向推论时“形”是否能转化为原有的“数”，这就是双向性原则的含义.最后，要在实践中不断地创新.数学思维整体上比较抽象，随着教学活动和教学目的的变化，教师在运用数形结合方法时也需要结合实际需要对其教学方法进行适时的改变.切忌一成不变、照本宣科.

二、在高中教学中数形结合的具体应用方法

1.以形释数

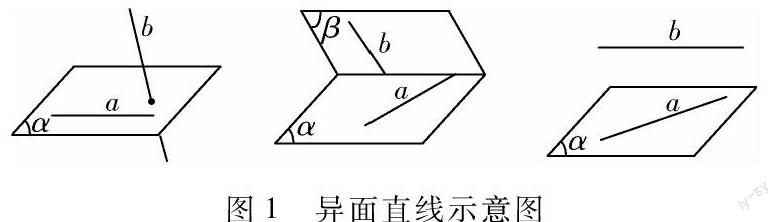
掌握空间几何的基本概念，消除固有的几何知识的思维模式，了解常见公理.掌握数形结合的方法后，即使是概念很抽象的立体几何，也能通过直观的图形表现出来.例如理论知识中的异面直线，仅凭讲解与学生的想象很难让学生对这些知识有深刻的认识，而采用几何图形（图1）进行讲解后，该理论则得到了很好的阐释.学生也对异面直线的定义有了深刻的认识.

2.通过图形反映记忆公式

学生在学习数学过程中，最头疼的就是公式的诵记.有些公式，例如与三角函数相关的便有不下几十个，很难一字不差精准地记下来.但是，采用数形结合的方法教学，学生在看了图形之后对理论公式有了更直观的理解，则容易记忆多了，并依据数形结合，总结出“奇变偶不变，符号看象限”的口诀.

3.通过图形统计概率

解答概率题时，先要列出图表中的重要数据，认真观察图形从而正确解题.通过表格中给出的数据联想构建出一个恰当的图形.让学生更好地理解概率的含义.将表格信息图像化后能将复杂的概率问题简单化，同时，课堂授课形式也变得多样化.通过图形，表格中数据组的特征被表现出来，其变化情况也更为直观，大大简化了学生的解题过程.

三、将数形结合方法运用于高中教学的意义

1.帮助学生更深刻形象地理解理论知识

高中的数学课程总体来说难度较大，逻辑性较弱的学生无法真正地理解抽象的理论知识，数学成绩始终无法突破.例如要运用大量公式的三角函数，彼此之间关系错综复杂，如果不能进行理解性记忆，那么将无法真正地掌握这一版块的知识，这种情况下，采取数形结合的方法则能够帮学生有效地完成知识的衔接与消化.

2.帮学生建立起数学学习兴趣

在高中的整個数学学习过程中，关于函数和解方程部分的内容是比较枯燥的，当学生无法理解课程内容时，便会产生消极情绪，从而恶性循环.在整个数学知识框架的构建中，学生最薄弱的环节便是理论知识的学习.在这种情况下，教室用数形结合的方法将抽象的理论知识讲话为可见、可理解的知识、调动学生的直观思维从而产生兴趣，这样在很大程度上能提高授课效率.

3.帮学生建立多面性的数学思维

学生在学习涉及公式理论较多的数学知识时，例如直线和圆锥曲线课程，这些课程不仅仅有代数，还有图像，二者的完美结合则需要运用到比较成熟的数形结合方法.老师在授课过程中使用数形结合方法，潜移默化地培养学生的数学思维.将抽象思维与直观思维有机结合，培养思维的灵活性，快速消化相关知识.

四、总结

综上所言，只要遵循一定的原则和策略，好好利用这一方法教学，就一定会在一定程度上强化学生的理解能力和学习能力.提高学生的学习兴趣，提高学习成绩.将数形结合这一方法融入到实际教学中，可以培养学生对理论知识的有效衔接，强化学生的数学思维，形成数学学习源源不断的内核动力.

【参考文献】

[1]李花花.高中数学教学中运用数形结合的研究[D].提高解题能力，2011，15（11）：22-23.

[2]孙令伟.数形结合思想方法[D].在高中数学教学与解题中的应用，2011，15（01）：14-15.

[3]刘兴楠.数形结合思想在中学数学教学中的应用[D].建立直观数学思维，2009，11（02）：8-9.