ARIMA模型和X—11过程在农民人均现金收入预测中的应用研究

韩朝怡

[摘要]本文通过对我国2000-2014年的农民现金收入季度数据进行时间序列建模，利用ARMA模型和X- 11过程来分析预测短期内我国农民现金收入的变动趋势，为短期内预测我国农民现金收入提供有效参考。

[关键词]农民现金收入；时间序列分析；ARIMA模型；X- 11过程；R语言

[DOI]10.13939/j.cnki.zgsc.2015.23.021

1 引 言

农民增收是解决“三农”问题的核心任务之一。农民收入按收入的形态可分为现金纯收入和实物纯收入。实物纯收入是农民自产自用的粮食等农产品按市价的折价收入。农民人均现金收入由工资性收入、家庭经营收入、财产性收入构成，均以现金计量，数据更具有准确性。

2 时间序列分析及ARIMA模型

时间序列分析（Time Series Analysis）是一种根据动态数据揭示系统动态结构和规律的统计方法。其基本思想是根据系统的有限长度的运行记录，建立能够比较准确地放映时间序列中所包含的动态依存关系的数学模型，并借以对系统的未来进行预测。

ARIMA （Autoregressive Moving Average）模型即自回归移动平均模型，适用于各种时序数据，该模型是博克斯—詹金斯（Box-Jenkins）在1976年提出的，其基本思想是将时序数据序列视为一个随机序列，其单个序列然具有不确定性，但整个序列的变化却有一定的规律性。具有如下结构的模型为求和自回归移动平均模型，简记为ARIMA（p，d，q）模型：

其中， 分别为d阶差分平稳可逆ARIMA（p，d，q）模型的p阶自回归系数多项式和q阶移动平滑系数多项式，为零均值的白噪声序列。

3 ARIMA模型建立与预测

3.1 数据的选取

本文数据选取自《中宏数据库》，选取自2000年第1季度至2014年第3季度的全国农民人均现金收入，通过ARIMA模型，进行预测。

3.2 数据平稳性检验

ARMA模型应用的前提条件是时间序列是平稳的，即其均值与时间无关，其方差有限。因此，通过r语言读取出农民人均现金收入（money），发现农民人均现金收入具有明显的上升趋势和季节趋势。因此，为消除长期趋势和季节趋势，先后进行一阶差分和季节差分，经过差分后的农民人均现金收入在0值附近上下波动。故本文运用R语言，采用单位根检验法（ADF检验）判断该序列是否为平稳序列。单位根检验原假设Ho：单位根等于1；备择假设H₁：单位根小于1。对一阶差分后的出口额进行ADF单位根检验，p=0.01，拒绝原假设，故一阶差分出口额（dle）序列属于平稳时间序列。

3.3 模型的识别与定阶

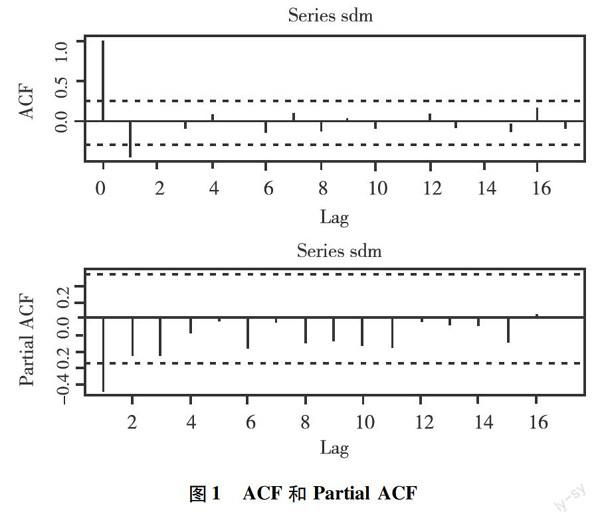
通过考察平稳后时序的自相关函数和非自相关函数的形状及性质，对时序模型作最初的判断。ARMA模型建模的规则是，如果自相关函（ACF）数为指数衰减，偏自相关函数（PACF）在p步以后截尾，则此该时间序列模型为p阶自回归模型AR （P）；如果自相关函数在q步以后截尾，偏相关系数为指数衰减，则此该时间序列模型为q阶移动平均模型MA （q）；如果自相关函数在q步以后截尾，偏自相关函数（PACF）在p步以后截尾，则可判定该序列为ARMA（p，q）序列，故首先绘出进行一阶差分后及季节差分后的农民人均现金收入（sdm）的ACF、PACF图。从图1可以看出，自相关函数ACF -步截尾，PACF指数衰减，故先建立ARIMA（0，1，1）模型。

3.4 参数估计

由于农民人均现金收入（ Money）具有季节性和长期趋势，故对建立季节乘积模型SARIMA （0，1，1）×（0，1，1）₄，通过AIC准则对所建模型的比较，最终建立疏系数SARIMA（0，1，1）×（0，1，1）₄模型。

3.5 模型的诊断

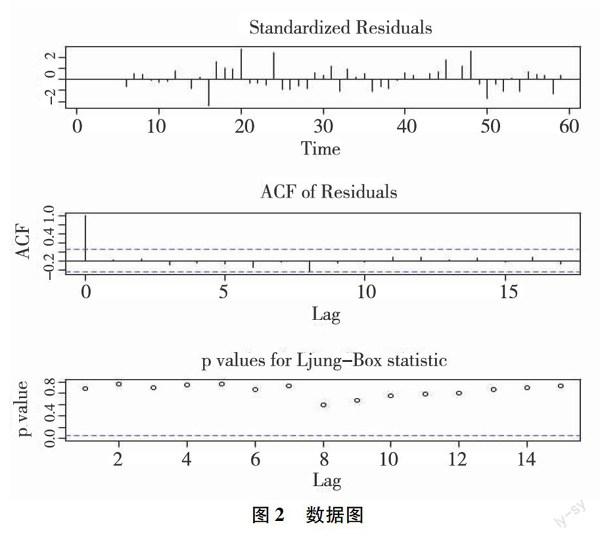
对所建模型模型的残差进行白噪声检验，选用Ljung-Box检验统计量，原假设H₀：残差是白噪声序列，若不能拒绝原假设，则说明模型建立效果较好，残差中不存在

残差的标准差均集中在-2到2之间，残差的自相关图ACF均位于置信区间内，Ljung-Box统计量的p值均大于0.05，故不能拒绝原假设，即残差是白噪声序列，模型拟合效果较好（见图2）。

3.6 预测

模型对2014年第3季度、2015年第1、2季度预测。

4 Xll方法的应用

4.1 去除季节趋势

利用Eviews6.0进行操作，首先打开农村现金收入（shouru），通过观察其原数据发现该数据具有明显的季节趋势和长期趋势，故先利用X-11技术滤掉季节趋势，得到提取出的季节因子序列、滤掉季节趋势之后的出口额徐磊，以及随机因子序列。

4.2 建立回归模型

观察滤去季节性现金收入（shouru_sa）与时间t的关系，发现两者呈二次函数的关系，故进行二次函数拟合，然而由于误差具有自相关，故建立X.= 633. 25+0.8243t²+0.4972X_t-1，X_t置为农村居民人均现金收入。

4.3 模型检验

根据所建模型进行样本内预测，根据误差公式e 得到误差值与真实值的误差，发现样本内预测值与真实值的误差率均在5%以下，模型拟合效果良好。

4.4 模型预测

乘季节因子即可得到农民人均现金收入预测值。

5 模型的比较

对两种方法所建模型进行比较，如下表所示。

ARIMA模型与X-11方法所得到的预测值发现其预测值相差较少，两种模型拟合效果良好。