Mathematica绘图功能在微积分中的实践应用

李娅　李红捷　杨雪

[摘 要]计算机与数学教育的结合，使得掌握数学知识与提升计算机能力同步进行。Mathematica是目前使用最广泛的数学软件之一，它能够通过简洁自然的命令完成求值、导数、积分、数值解方程等运算。微积分的研究对象是函数，而函数的很多性质如连续性、可导性等都可以通过图像体现出来。而Mathematica软件能够准确快捷地绘制函数图像，从而对函数的性质有直观形象的认识。本文以跟sin有关的几个函数为例，探讨Mathematica的绘图功能在微积分教学和学习中的辅助以及实践应用。

[关键词]Mathematica 极限 无穷大 无界 单调性 导数

[中图分类号] G642.4 [文献标识码] A [文章编号] 2095-3437（2015）03-0160-03

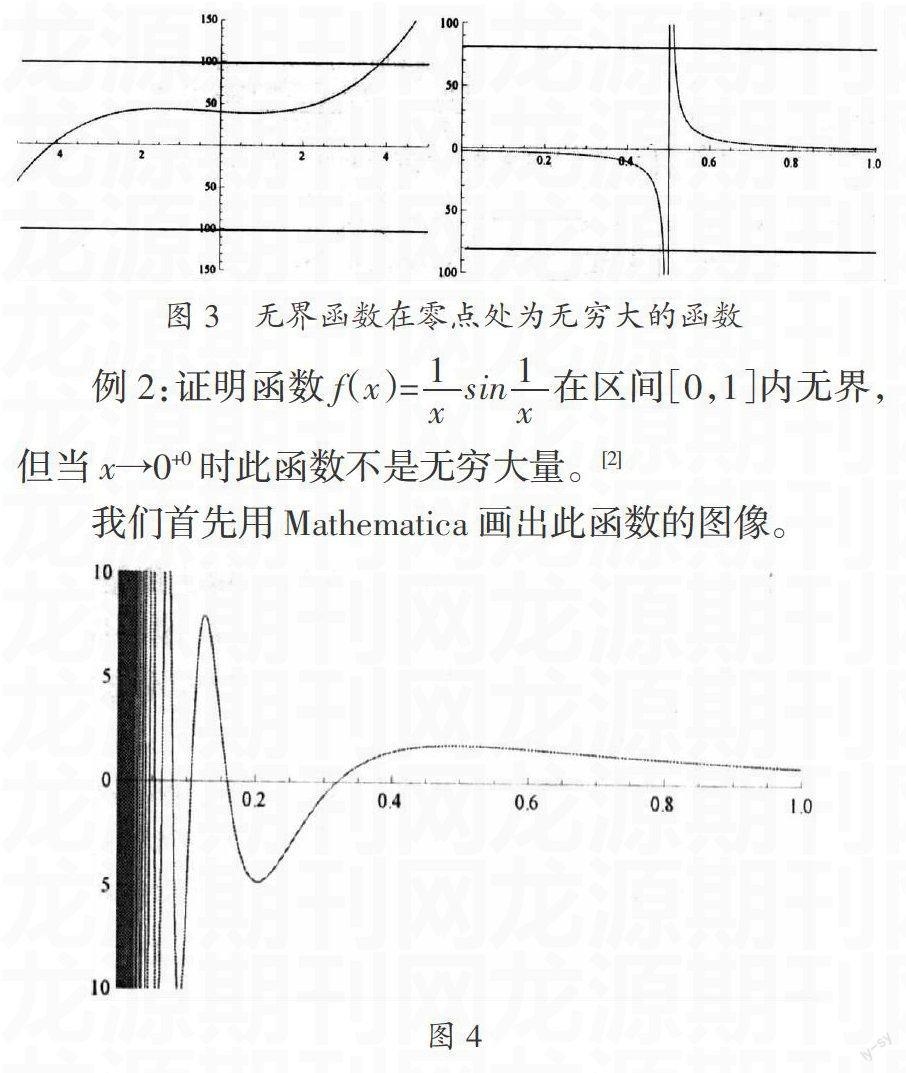
数学分析或高等数学等微积分课程是高等院校理工科学生最重要的基础课，对学生的逻辑思维的培养以及专业知识的学习与研究等方面都具有举足轻重的作用。微积分的研究对象是函数，函数的很多解析性质都能通过函数图像体现出来。我们可以通过函数的单调性、凹凸性等性质定性地绘制函数的图像，从而借助图像可以对函数的性质有个直观上的认识。但是如果函数比较特殊，例如函数f（x）=sin，有时很难利用此方法去定性画图，此时，我们可以借助计算机软件来进行作图。相比手工作图，软件作图具有操作方便，结果准确直观的特点，能够更好地对函数的微积分性质有初步了解。本文通过几个例子说明Mathematica软件作图在一元函数极限、有界性和无穷大、单调性几个方面的应用。

一、Mathematica绘图在极限上的应用

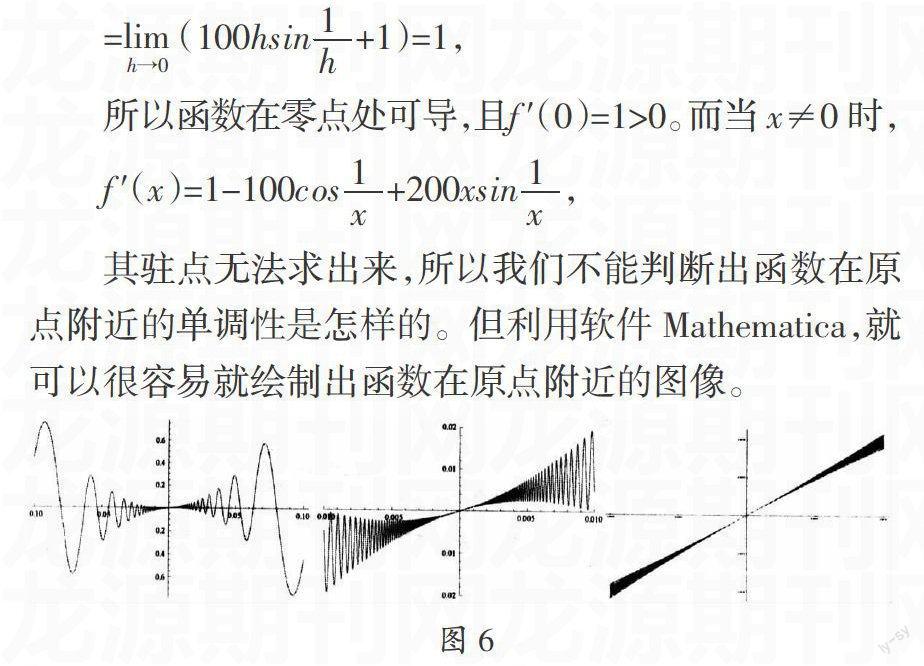
从上图可以看出，函数在原点附近振荡，且距离原点越近，振荡频率越快。无论取多么小的邻域（-δ，δ），函数在此邻域里都不是单调变化的。这个函数的性质表明，由函数在零点处导数大于零，不能保证函数在零点的邻域上单调增加，所以命题是错误的。

上述例子可以看出，利用Mathematica绘图功能，函数的很多微积分特性就一目了然了。

四、结论

计算机得到广泛应用以来，已经成功发展成为重要的工具，用以补充经典数学。函数性质图形化的过程是数学与计算机技术结合的过程，在这一过程中，数学思维能力、数学语言表达能力、计算机应用能力得到综合体现。本文通过和sin有关的几个函数分析性质的研究，揭示了Mathematica数学软件作图在微积分教学和学习中的重要作用。它具有定性作图方法不可比拟的方便性、快捷性和准确性，使学生对高等数学的主要概念和性质有更好的理解和认识。除此之外，Mathematica拥有强大的数值计算和符号计算功能，可以进行求导、积分、方程求解、矩阵计算等，和其他应用软件之间也可以方便地调用，因此在工程、物理等方面也有广泛的应用。由于软件能够用很少的代码完成其他软件相同的工作，界面友好，因此学生很容易掌握此软件的运用，不仅可以借助它来学习基础知识，而且对后续的专业课程和研究工作来说，此软件也是一个有力的辅助工具。

[ 参 考 文 献 ]

[1] 张韵华.符号计算系统Mathematica教程[M].北京：科学出版社，2001.

[2] 吴纪桃，魏光美，李翠萍，柳重堪.高等数学（第二版）[M].北京：清华大学出版社，2011.

[3] 冯伟杰，魏光美，李美生，吴纪桃.高等数学习题课教材[M].北京：清华大学出版社，2012.

[责任编辑：林志恒]