“平面直角坐标系”导学
田载今

人教版初中数学教科书中,第七章“平面直角坐标系”包含两节内容.前一节引入了平面直角坐标系,从而给出了描述平面内任一点的位置的工具:后一节讨论:坐标方法的简单应用.点是构成图形的基 本元素,坐标由有特定含义的数构成,点与坐标之间的相互转化,是形与数的转化,坐标方法是数形结合的产物。 :
1.坐标是对点的位置的数量化表示.
任何几何图形都可以看作点的集合,几何巾的点本身没有大小,只表示特定的位置,如何精确地描述点的位置?这是数学中的一个基本问题.
如果要研究的点恰好都在同一条直线上,那么我们可以选这条直线为数轴,取它上面的一个定点作为原点,再规定出单位长度和正、负方向,则这条直线上原点之外的任一点P到原点的距离及点P在原点的哪一侧就随之确定了,于是,点P的位置就能用它对应的数x表示了,x的绝对值表示点P到原点的距离,x的正负表示点P在原点的哪一侧,x叫作点P在这条数轴上的坐标,我们已经知道,数轴上任一点都对应一个确定的实数,反过来,任一实数都对应数轴上唯一的点,因此,数轴是能精确地描述同一条直线上点的位置的数学工具,数轴上的所有点与全体实数有一一对应的关系.
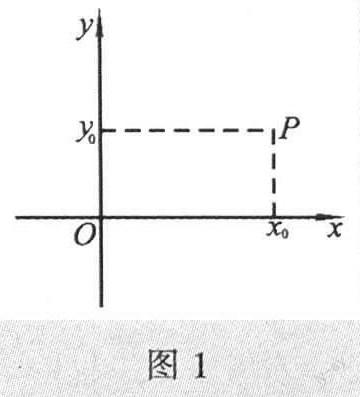
如果要研究的点都在同一平面内,但不都在同一条直线上,那么用一条数轴就无法描述这些点的位置了.于是,有人想到用两条数轴解决问题,如图1,画一条水平方向的数轴,取向右为正方向,记作x轴;过x轴的原点O再画一条竖直方向的数轴,也以点()为原点,取向上为正方向,记作y轴,这就组成了一个平面直角坐标系.从平面直角坐标系内的一点P,分别向x轴和y,轴作垂线,垂足分别对应x轴上的数x0和y轴上的数Yo,这样点P就与有序数对(xo,yo)对应起来了,(xo,yo)即为点P在这个平面直角坐标系内的坐标,按照这种方法,平面内任一点都有一个有序数对(x,y)形式的坐标,而且不同的点的坐标不相同:反过来,任一有序数对(x,y)在平面内只对应唯一的点.因此,平面直角坐标系是能精确地描述平面内点的位置的数学工具,一个平面内的所有点与全体有序实数对有一一对应的关系,
比较上述两类问题,可以发现:确定直线上点的位置时,用一条数轴,点的坐标为一个实数,这叫作一维坐标;确定平面内点的位置时,用两条数轴,点的坐标为两个有序的实数,且不同位置上的实数各自有着特殊的意义,这叫作二维坐标.可以进一步想到,确定空间中点的位置时,要用三条数轴,点的坐标为三个有序的实数,且不同位置上的实数各自有着特殊的意义,这叫作三维坐标,这些坐标都是在不同条件下对于点的位置的数量化表示,且在日常生活中都有所体现.例如,在沿一条画好的直线植树时,如果给出了这条直线上的一个定点作为参照点,那么只用一个数就能表示某个植树点在参照点的哪一侧,离参照点有多远:在一张方格纸上描点时,只用两个数分别表示行号和列号,就能准确地描述要描的点的位置:去一个楼上、楼下都有座位的电影院看电影时,根据电影票上分别表示楼层、排号和列号的三个数,就能准确地找到自己的座位.
2.坐标方法是重要的数学方法,
数学研究的主要对象是数量关系和空间形式,这两者不是截然分离的,而是密切相关的.坐标方法的作用并不局限于给出点的位置的数量化表示,也不仅是能对平移等图形变化给出数量化描述.坐标方法的重要贡献在于为形与数的转化提供了有效途径,从而建立了点与坐标的对应关系,这不仅把点的位置用数的形式表示了,而且也给用数量关系刻画几何图形提供了方便,例如,等式y=2x表示y与x的数量关系,当x分别取0、±1、±2、…时,y的值分别是0、±2、±4、….我们把有这种关系的x和y分别作为点的横坐标和纵坐标(x和y也叫坐标分量),则以这样的有序数对(x,y)为坐标的点包括(-2,-4),(-1,-2),(0,0),(1,2),(2,4)等,所有满足y=2x的点(x,y)在平面直角坐标系内构成一条直线(如图2),我们称它为直线y=2x.于是我们既可以利用这条直线直观地研究y=2x这一数量关系,又可以利用y=2x这一式子研究这条直线.
坐标方法的出现,使几何问题可以代数化,即找出图形上点的坐标分量应满足的数量关系,从而得到图形对应的方程,通过讨论方程来研究图形.这种方法的创立者是法国的哲学家和数学家笛卡儿(Descartes.1596-1650).他的哲学著作《方法论》的附录《几何学》,集中反映了平面坐标方法和变量思想.尽管笛卡儿最初提出的平面坐标系与现行的平面直角坐标系在具体形式上有差别,但是他的思想引导了解析几何的诞生.解析几何这一用代数方程研究几何图形的数学分支,又为微积分的诞生创造了条件.恩格斯对此的评价是:“笛卡儿变数(即坐标)的出现,是数学中的转折点,从此运动和辩证法进入了数学,微积分的出现也成为必然.”
数学家华罗庚认为,数无形,不直观,形无数,难人微,在后续学习中大家会看到,坐标方法既可以为函数建立图象,使得抽象的数量关系得到直观的几何解释,又可以将几何图形数量化地表示出来,通过对数量关系的定量研究更细微地认识图形.坐标方法有如此重要的作用,是因为它把数与形完美地结合起来,使得它们优势互补、相得益彰.
3.坐标方法的应用一例,
坐标方法有着广泛的应用,本章中主要介绍了用坐标表示地理位置和平移变换,除了平面直角坐标,还有极坐标等可以确定点在平面内的位置,极坐标也是有序数对,其中两个坐标分量分别表示距离和角度,教科书第74页“思考”中的问题就适合用这种形式的坐标解决.虽然它与平面直角坐标有区别,但是它们的基本思想是相同的.
有了坐标方法,可以使解决问题的思路更宽广,甚至可以通过精确的作图代替复杂的计算.下面的问题如果不用坐标方法,则要等我们到高中学习了正弦定理等知识以后才能解决,但是如能灵活运用坐标方法,我们现在也能解决它.
问题从海岸上A地测得小岛C在北偏东40°方向,从海岸上B地测得小岛C在北偏西50°方向,A地在B地的正西方向,两地相距lkm.你能否求出小岛C到A、B两地的距离?
分析:已知条件中有两个方位角和一个距离,要求两个距离,可以先建立适当的平面直角坐标系,表示出A、B两地的位置,再进一步确定小岛C的位置.
解:如图3,以A地为原点,以正东方向为x轴的正方向,以正北方向为y轴的正方向,以1个单位长度表示1km,建立平面直角坐标系,
根据A地在B地的正西方向,两地相距1km,可确定点B在x轴上,它的坐标为(1,0).
自点A画出北偏东40°方向的线,白点B画出北偏西50°方向的线,两线的交点即为小岛C所在的位置.度量图中线段AC、BC、AB的长度,并以图中线段AB的实际长度为1个单位长度进行同比例换算,可得AC≈0.64,BC≈0.77,从而可知小岛C到A、B两地的距离分别约是0.64km、0.77km.
上面的解答先利用坐标方法确定点的位置,再通过度量线段的长度并计算,解决了问题,这种方法在实际测量中也经常用到.
平面直角坐标系是数形结合的重要工具,我们在以后的学习中还会经常用到,希望同学们学好本章内容,不断加深对坐标方法的认识.

