贵州省民族地区初中学生数学课程的学习适应性评价

冯新骅 吴畏

【摘要】本文专注于对初中学生数学课程的学习适应性評价。基于项目反应理论的等级反应模型以及收集自贵州省民族地区的测试卷和问卷数据引入了带有客观适应性和主观适应性新概念的模型来评价学生的潜在特质，即适应性。本文得到了各学生的适应性结果以及少数民族地区的基本结论。最后给出了一些思考与建议。

【关键词】学习适应性评价 贵州省民族地区 项目反应理论

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2015）03-0149-02

《义务教育数学课程标准（2011年版）》实施以来，在全国各地，尤其是教育发达地区得到了很好的贯彻，但在少数民族地区，由于历史与社会原因造成的以数学学科为代表的理科教学质量与学生成绩的落后现象仍然存在。民族地区如何结合自身实际情况有效实施新课程标准，如何有效把握学生对数学课程的适应能力成为急需解决的问题。本文将基于项目反应理论，尝试通过定量的研究方法建立新的学习适应性评价指标，刻画学生个体和地区整体的适应性，为问题的深入分析与进一步解决提供支持。

1.研究对象

为了研究民族地区学生真实的数学学习状况，同时最大程度地刻画出民族地区学生这一特定群体对数学新课程标准下知识安排和教学方式的适应能力，本文使用了“适应性”（adaptability）来描述这种“特质”（trait），这种特质包含了以下两个主要方面：

（1）对《数学课程标准》的适应性，即是否能够适应目前新课程标准在教学内容和教学目标上的具体要求。新课标不仅要求学生掌握基本的数学知识和基本技能，培养对数学的兴趣，还要求其具备一定的科学素养，能够运用所学知识解决实际数学问题。[1]

（2）对教材和课堂教学的适应能力。适应性好的学生应该能合理使用教材，高效参与课堂教学与讨论，保质保量完成作业，同时不受到教材和教师的制约与影响。

2.研究方法

本文主要采用测试卷和调查问卷数据的定量分析法，基于项目反应理论并结合经典测量理论探究学生数学课程的学习适应性，综合访谈信息得出相关结论。

2.1样本数据的基本情况

本研究的被试者为八年级学生，来自贵州省6个民族自治县的9所中学以及贵阳市的一所初中。共发放测试卷和问卷545组，涉及汉族以及苗、水、土家、布依、仡佬、侗等主要世居民族的学生，有较强的代表性。

测试卷数据包括原始的百分制得分以及根据知识点掌握程度划分的等级得分，调查问卷数据采用等级评分制。

2.2模型介绍

项目反应理论（IRT）运用概率函数的形式描述了项目作答反应结果如何受到被试者能力水平和项目特性联合作用的影响，并依据被试者的各项目实际作答来刻画其能力水平。

本研究采用该理论多级记分模型中应用最广的等级反应模型（GRM）。考虑到测试卷题目所采用的均为主观问答题，而问卷理论上也不存在客观猜测的问题，最终模型采用不含猜测参数的双参数模型：

p■■（？兹）=■

p■■（？兹）=p■■（？兹）-p■■（？兹）[2]

其中？兹即为本研究中的适应性，p■（？兹）表示适应性为？兹的被试者在i项目上正确作答的概率。bij为项目i第j等级的难度，p■■（？兹）为被试者得到等级j及以上的概率。

2.3 评价指标介绍

根据模型可以得到被试者在测试卷和问卷中的不同适应性？兹，但实际上两者存在一定区别。测试卷是依据新课程标准编制的，着重考查学生在学习过程中对数学基本知识和基本技能的实际掌握，是一种客观考核，可定义为客观适应性。与之相对，调查问卷从数学思考、问题解决和情感与态度等方面考查学生对数学学习、数学课程和数学教学的认知程度[3]，包含了学生对自我学习习惯、学习态度和兴趣等方面的主观评价，可定义为主观适应性。

单纯的主观或客观适应性并不能真正反映学生对新课标数学课程学习的适应程度，二者的一致提高才是我们希望看到的良好态势。宏观而言，二者的相关性能很好地刻画一个地区的整体适应程度。主客观适应性差异较大的地区，即使学生平均成绩较高，也不能认为很好地落实了新课标精神，因为数学成绩的提高很可能是以挤占学生其他时间，牺牲学生学习兴趣为代价的。由此，我们引入协调适应性概念作进一步探究。

3.基本结果

利用PARSCALE软件对模型的项目参数进行估计[4]，结果如下：

3.1模型的基本结果

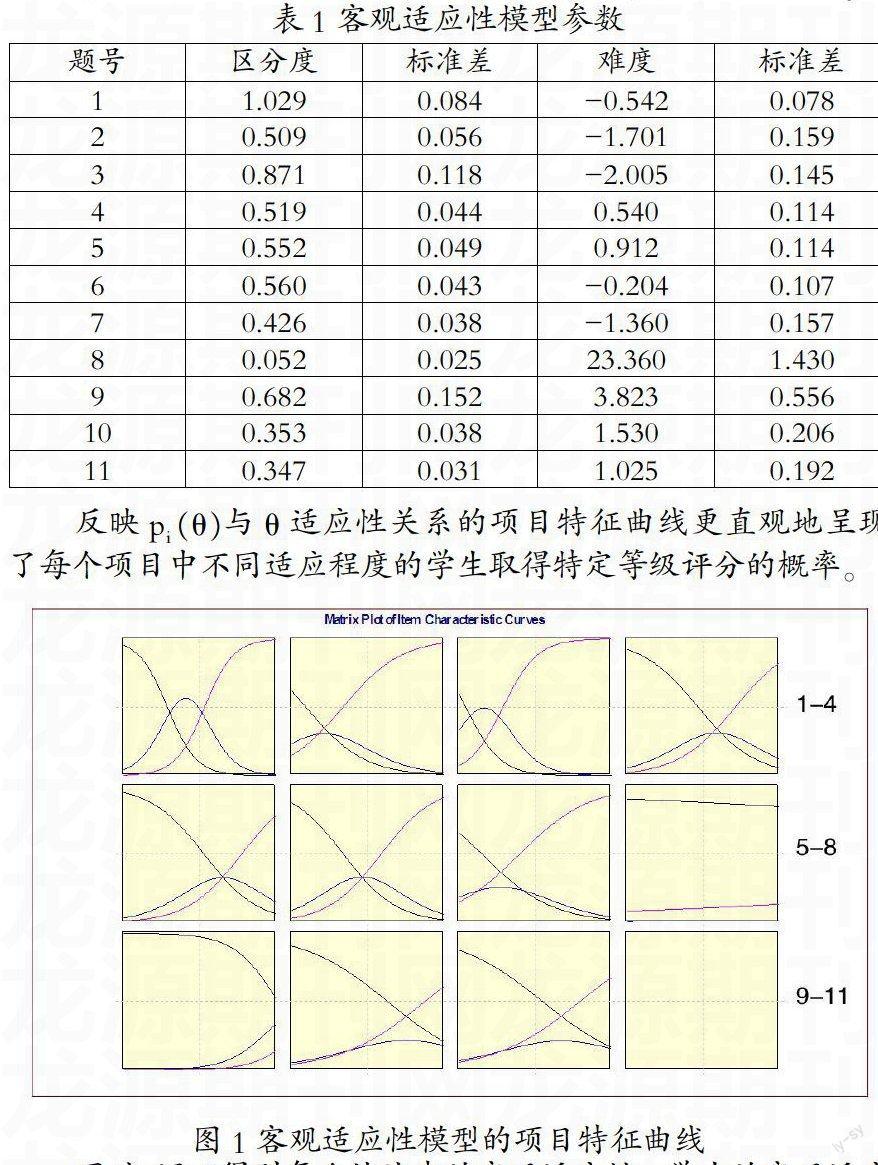
如表1和图1所示，多数题目具备良好的难度和区分度，唯一不太理想的第8题所考查的分段函数是在初中阶段难度较大的内容，有限的测试时间里仅部分学生完成了部分解答。区分度最大的1、3题考查的分别是几何与代数内容中的基本概念，从侧面也体现了基础知识的牢固掌握在数学学习中占有关键地位。

表1 客观适应性模型参数

反映p■（？兹）与？兹适应性关系的项目特征曲线更直观地呈现了每个项目中不同适应程度的学生取得特定等级评分的概率。

同时，还可得到每名被试者的客观适应性。学生的客观适应性与原始得分之间的相关性系数高达0.914（p<0.01），这是在对每道题的评价尺度由约10分评分范围调整为三个等级的情况下实现的，从一个侧面印证了模型合理性。

使用因子分析对问卷数据进行单维性检验时发现，第一与第二特征值之比和测试卷数据相近，近似符合单维性假设。因此可参考得到主观适应性模型参数（略）。本文使用“差异度”和“认知度”来对应客观适应性模型中的区分度和难度参数，对于认知度要求较高的项目，学生的主观适应性趋向于积极的概率较低。

从结果看，认知度要求高的问题主要集中在课堂效率、习题类型、主动提问等环节，差异度最大的也是课堂效率，这固然与学生的学习态度、学习基础有关，但在一定程度上也反映了教师课堂教学水平的参差不齐。

3.2 适应性的综合评价

根据3.1的结果可以得到个人适应性情况。

如图2，个人的主、客观适应性之间具有一定程度的正相关性（0.328？鄢？鄢， p<0.01）。但两者都比较低的学生人数仍然较多，内部差异明显。根据贵州调研的两条线路可划分为南部和北部，两地在协调适应性上差异显著（南部0.157，北部0.487）。其中客观适应性基本一致，但主观适应性方面南部要远高于北部。两地的主要外部差异在于语言和社会经济发展方面，北部的少数民族汉化程度高，各民族之间交往与融合的程度也更高，而南部的民族风俗习惯保留更为完整。

结果可从两方面考虑，在民族传统风俗习惯保留较为完整的地区，一是学生的自我评价尺度更为宽松，或者对待学习的态度更趋向于求知本身而非应试，学生的学习兴趣更浓厚，没有过多地受到应试教育的影响；二是新课程标准的影响力有限，理念渗透和实施贯彻缺乏年轻教师的实践与传播。

逐一检验两地问卷中的差异性，可以发现在对待难题的态度、提问的频率以及数学知识在生活中的应用等方面均存在显著差异，南部的态度更为积极。而在对待教材编排、习题安排的态度以及课堂效率等方面则无显著差异。因此，南部协调适应性更低的原因主要在于学生的学习积极性与客观条件限制的矛盾，学生比较积极的动力并未完全转化为适应性能力的提升。这对教师提出了更高的要求，如何有效提升课堂效率使得学生能在过程、结果上都适应课程标准的要求，如何更切合实际地组织课堂教学和课外实践都值得进一步思考。

4.结论与思考

从贵州省民族地区初中学生数学课程的适应性情况出发，结合调研中收集的听课和访谈信息，可以发现学生对于数学本身是有一定兴趣的，对待学习的主观认知上总体积极，但这种兴趣与积极性并未有效转化为适应性的提升。在县城以外的乡镇初中，能够严格按照新课标的要求并结合当地实际开展有效的实践探究活动的课堂确实很少，更多是形式化的探究活动，既没有充分应用好学生的积极性，也没有使得学生巩固夯实好课程标准中的基础知识。

因此，解决民族地区初中学生数学课程适应性差的问题不应忽视以下两方面。第一，更多关注学生个体，认识与把握好学生个体的学习兴趣与积极性。学生的个体差异明显，尤其初中生正处于身心发育的关键时期，要给予学生更多关爱，引导他们把对数学的兴趣和积极性转化为学习数学知识的动力，进而养成更好的学习习惯。第二，要重视软件投入，尤其是教师队伍建设和教师培训。教育资源要更多流向师資力量薄弱的地区，开展的培训要更多针对课堂教学实践和教师业务知识，教师要学会如何利用好学生的学习兴趣，同时要反思如何能将学生的困惑在课堂上更有效地集中解决。

参考文献：

[1]义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]Samejima，F.Estimation of latent trait ability using a response pattern of graded scores[M].Psychometrika Monograph Supplement，No.17.1969

[3]何伟，李明杰. 我国少数民族地区学生数学学习态度的调查分析与思考[J].民族教育研究，2014，（1）.

[4]Mathilda du Toit. IRT from SSI： BILOG？鄄MG， MULTILOG， PARSCALE， TESTFACT [M]. Science Software International， Inc. 2003.

作者简介：

冯新骅（1989-），男，汉族，浙江建德人，中央民族大学理学院2012级硕士研究生，研究方向：数学教育，教育统计。