在立式加工中心上实现α°幅板面上孔倒角的分析及改进
万莲翠

摘 要:从程序及在实际加工中分析斜面上孔的倒角量不均的原因,且随着角度的增大而越明显,为了提高车轮加工效率,文章利用圆柱曲面与圆锥曲面的交线建立刀具轨迹,从而实现在立式加工中心上加工α°幅板面上孔的倒角。
关键词:车轮倒角;立式加工中心;曲线;刀具轨迹;圆柱面;圆锥面
1 问题提出及分析
目前,工艺上将机车车轮孔的加工定在立式加工中心上进行。SS6B车轮观察孔?准60mm两侧倒角均为C2,因内侧面为5°斜面,所以采用三轴联动螺旋铣(1/4),但在螺旋起点及终点出现了倒角量不均的现象,由此分析这种现象会随着斜面角度的增大而越明显。
在HXD3车轮试制过程中,内侧面10°斜面上孔的倒角同样采用螺旋铣,出现了最高和最低处加工不上的情况,针对此种现象若将倒角工序调整到组装一组砂轮打磨,因车轮成批加工效率不高;采用数控自动编程,程序将冗长而繁琐,不宜修改和检查。寻找更合适斜面上孔倒角的加工方法是必须的。
2 图形数学分析
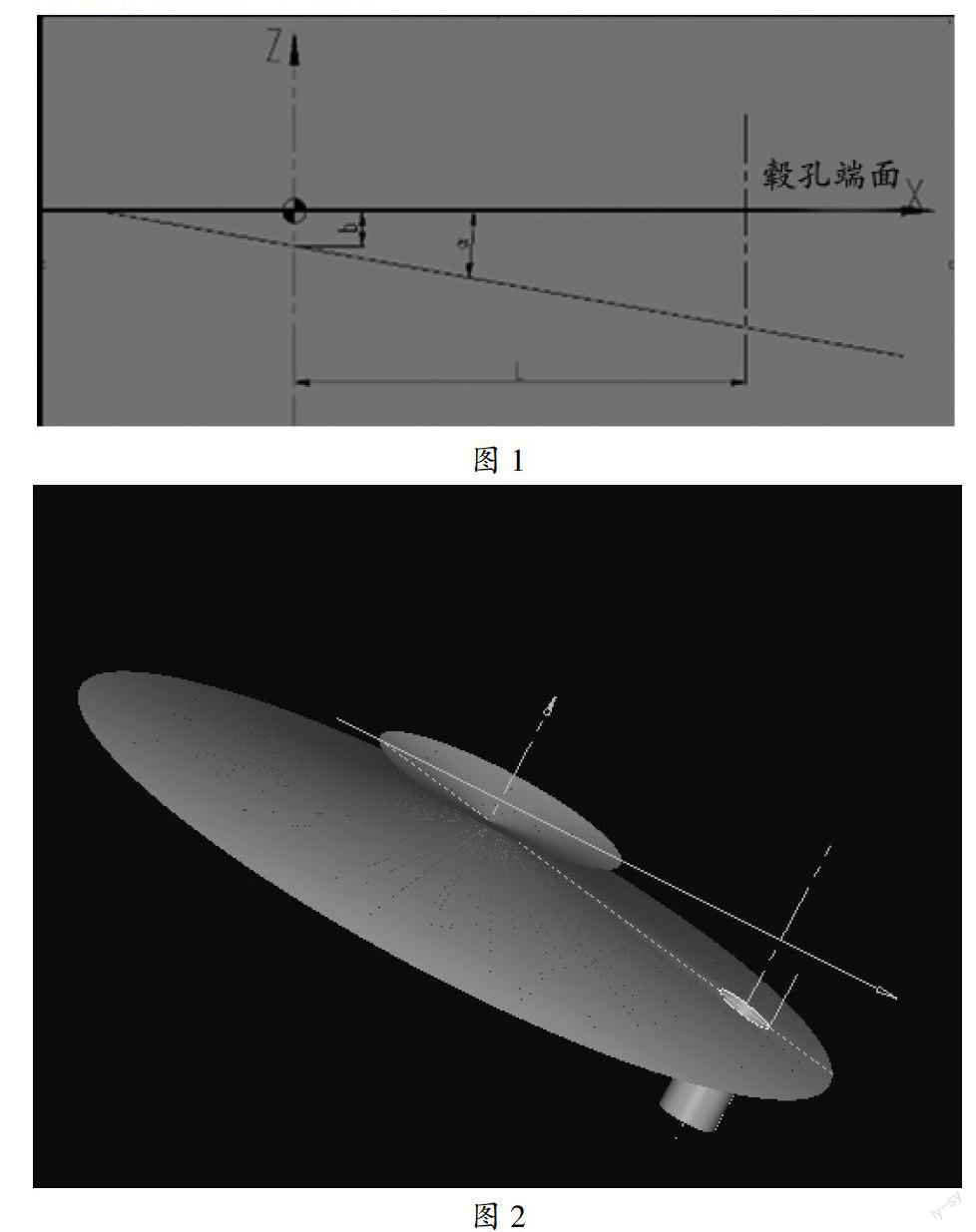
如图1所示,参数:(1)斜面角度α(和毂孔度面的角度);(2)斜面距离毂孔端面距离:b;(3)工艺孔距离毂孔中心的距离:L;(4)工艺孔从数学角度分析,α斜线围绕毂孔中心线旋转(360°)形成圆锥曲线,工艺孔(r)围绕本身的中心线(距离毂孔中心距离L)旋转(360°)形成半径为r的圆柱曲面。两曲面在高度h上存在相交线,建立曲面图形如图2所示。
经过分析,圆锥曲面与圆柱曲面的交线即为刀具轨迹。曲线的刀具轨迹生成是实现加工的关键环节,它是根据所选用的加工机床、刀具、走刀方式以及加工余量等工艺方法进行刀位计算并生成加工运动轨迹。
刀具轨迹的生成能力直接决定数控编程系统的功能及所生成加工程序的质量。高质量的数控加工程序除应保证编程精度和避免干涉外,同时应满足通用性好、加工时间短、编程效率高、代码量小等。
3 刀具轨迹方程
3.1 以两曲面的交线为刀具的加工轨迹实现斜面上孔的倒角
斜线方程:z=-tgα?鄢x+t(t=b) (1)
圆柱面方程:(x-L)2+y2=r2 (2)
轴线方程:x=L (3)
圆锥面方程(斜线绕Z轴旋转形成的圆锥曲面方程):z=±tgα×sqrt(x2+y2) (4);联立圆柱面曲线方程(2)和圆锥曲面方程(4)求解即为相交曲线,亦为刀具加工中心轨迹。相交曲线方程:(5)x z=(z-b)2/(tg2α?鄢2?鄢L)+L/2-r2/(2?鄢L);
(6)y z=±sqrt[r2-(x-L)2]
3.2 参数求解
求母线y=0 时的两个端点,即相交曲线的最高点和最低点。
y z=±sqrt[r2-(x-L)2]=0 (7)
解得;Xd1=r+L;Xd2=-r+L (8)
即Z最高点和最低点(Xd1,0,Zd1)、(Xd2,0,Zd2)将Xd1和Xd2分别代入式(5)或式(1),可求Zd1和Zd2
4 程式方程
#1=Xd1;#2= Xd2;#3=Zd1;#4=Zd2;#5=b;(有正负号)#6=L(有正负号)#7=r; (无正负号)#8=α;(与X向成锐角)#9=tan[#8];#10=k;(刀具Z向进刀值,具有正负向要求)#11=d;(刀补半径)
#19=p;(Z向递减值,有正负方向)G54G90G80G40;T1M06;G00X0Y0Z100;M03S1000;#2=#7+#6;
#1=[-1]*#7+#6;(L的正负使#1及#2具有正负号,符合程式要求)#3=#9*#2;#4=#9*#1;(但#3及#4只是程式的Z值,不符合程式要求,需要处理)#3=ABS[#3]*[-1];#4=ABS[#4]*[-1];(赋予程式坐标要求)X[#6];(圆柱面中心处)Z[#4+#10];N10G01G42X[#1+10]Y[-10]F200;
G02X[#1]Y0R10F70;#14=#4;N20#14=#14+#19;#15=2*#6*#9*#9;#16=#6/2;#17=2*#6;
#18=#7*#7/[#17];#12=[#14-#6]*[#14-#6]/[#15]+[#16]-[#18];(Xz)#20=[#12-#16]*[ #12-#16];#13=sqrt[#7*#7-#20];(Yz)G01X[#12]Y[#13]Z[#14]F40;IF[#14]GT[#3]GOTO20;
N30#14=#3;#12=[#14-#6]*[#14-#6]/[#15]+[#16]-[#18];(Xd)#20=[#12-#16]*[ #12-#16];
#13=sqrt[#7*#7-#20];(Yd)G01X[#12]Y[#13]Z[#14]F40;N40#14=#14+#19*[-1];#15=2*#6*#9*#9#16=#6/2;#17=2*#6;#18=#7*#7/[#17];#12=[#14-#6]*[#14-#6]/[#15]+[#16]-[#18];(Xz)#20=[#12-#16]*[ #12-#16];#13=sqrt[#7*#7-#20];(Yz)G01X[#12]Y[#13]Z[#14]F40;IF[#1T[#3]GOTO40;N50;#14=#4;#12=[#14-#6]*[#14-#6]/[#15]+[#16]-[#18];(Xd)#20=[#12-#16]*[ #12-#16];#13=sqrt[#7*#7-#20];(Yd)N60G02X[#1+10]Y10R10F70;G00Z50;X0Y0;M03S30;M05;M02;
程式说明:(1)此程序只适用于法拉克18i系统;(2)当加工多个孔时,将以上程序作为子程序,利用坐标旋转功能即可。
5 加工刀具轨迹调试及调整
工件加工程序改变,就必须按照首件加工的规定执行。
对HXD3车轮?准64mm侧面为10°斜面R5倒角加工进行首件试制为例。
整体硬质合金圆弧铣刀:31500-MEGA(R5)刀具参数:D=16mm,R=5mm;工件编程原点:毂孔中心;装夹方式及位置:轮缘踏面处三爪120°夹紧;1已知程式参数:L=325mm,r=32mm,b=-25.113mm,α=10°
(1)程式在机床上模拟:轨迹正确;(2)工件实际加工:给出刀补半径值(8)及刀补Z向走刀深度(-4.9)并计入:轨迹完全正确,加工参数合理,加工量均匀,粗糙度及加工形状完全符合图纸要求。
同样的,以SS6B车轮φ80mm内侧面为5°斜面C2倒角时给出刀补半径值(5)及刀补Z向走刀深度(-2)并计入(工件编程原点、装夹方式及位置均不变,45°倒角刀:ITC45/10-16R-40),加工轨迹正确,加工量均匀。
6 结束语
根据几何原理,求出圆柱曲面与圆锥曲面的交线方程,利用刀具加工轨迹原理建立了刀具中心轨迹,通过改变设定的参数即可求解不同角度上孔的倒角(如SS6B、HXD3),程序上做到了简单、方便、通用。这对于分析复杂曲线的特点与求解有很大的帮助。
——目镜套筒

