基于遗传算法的机床进给系统边界条件识别及动力学研究
刘周和


摘 要:文章借助于数学建模、力学分析、以及实验的方法,在构建滚珠丝杠力学简化模型基础上,对滚珠丝杠动力学性能进行研究,推导滚珠丝杠在集中质量的影响下以扭转、支撑弹簧支承的固有频率公式,在提出固有频率理论公式的基础上研究了梁结构的动力学性能,提出了基于遗传算法识别梁结构边界条件。利用实际的低阶固有频率和振型,辨识出工作台质量、支承轴承横向和扭转刚度。结果表明,该方法具有良好的识别精度,具有一定的工程实用性。
关键词:滚珠丝杠;特征方程;参数识别;遗传算法;固有频率
中图分类号:TH132 文献标识码:A 文章编号:1006-8937(2015)11-0090-02
关于机械结构的动力学分析,我们经常需要知道其结构参数及一些边界条件,识别结构参数,对于结构相对比较简单的一些部件,建立其有限元模型已不是难事,但是对于结构之间的连接部件,特别是一些相对复杂的支承结构,如轴承、弹簧等连接件,其有限元建模和测量都存在不小的难度,而这恰恰又是工程设计所需要的重要信息,因此,利用实验数据或者有限元分析识别连接部件或边界物理参数越来越受到工程师们的重视,也是近年来许多设计制造企业所关心的问题。
机床作为机械加工的重要工具,决定了工业加工的精度、速度和制造业的水平,机床进给系统的主要部件为传动丝杠、支撑轴承,工作台和驱动电机,他们的性能很大程度上决定了机床的质量和加工精度,研究进给系统的动力学性能对于机床,特别是应用广泛的数控机床有着非常重要的意义。
连续系统的模态振型理论研究已经比较成熟了[1-2],机床的主轴近似于一细长的梁,其横向振动[3]比纵向或扭转振动更为普遍,张会端[4]在弹性支承条件下建立了丝杠的频率方程和振型函数,并做了相关动力学分析,Gu UC、Cheng CC[5]研究了带移动质量块的Timoshenko[6]梁的横向振动,常见的结构参数识别方法有有限元法、直接法等来识别,朱坚民、张统超[7]利用试验模态和遗传算法对机床结合面参数进行了识别,并达到了较高的精度。
1 主轴丝杠横向振动的频率方程和振型函数
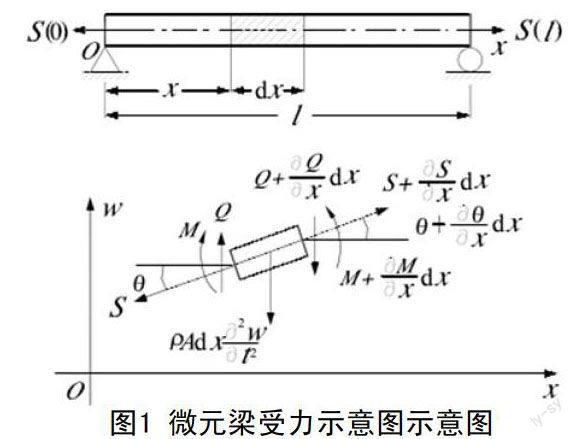
现在来考察等截面直梁的弯曲振动。取梁未变形时的轴线方向为x轴(向右为正),取对称面内与x轴垂直的方向为y轴(向上为正),如图1所示。梁在弯曲振动时,其挠曲线随时间而变化,可表示为下式。
梁微段沿横向所受外力有:梁微段对梁产生的力,剪力Q(x)和-Q(x-dx),以及集中质量所带来的力,忽略轴向力。根据Newton第二定律,梁弯曲自由振动微分方程为:
考虑轴承的支承刚度,其横向振动支承模型如图2所示。
两端的边界条件为:
EIY (2)(0)=kT1Y'(0),EIY (3)(0)=k1Y'(0),
EIY (2)(l)=kT2Y'(l),EIY (3)(l)=k2Y'(l),(11)
式中:
Y(x)为梁模型横向弯曲振动的模态函数;
EI为梁的抗弯刚度;
kT1、kT2为扭转弹性系数;
k1、k2为线弹性系数。
由(11)中的四个边界条件可以确定由四个方程组成的关于bn,n=1,2,3,4的线性方程组;且该线性方程组可以由BH=0的矩阵形式给出。H由bn,n=1,2,3,4确定;而B由bn的系数确定。因为bn不全为零,可以得到系数行列式
b11' b12' b13' b14'b21' b22' b23' b24'b31' b32' b33' b34'b41' b42' b43' b44'(12)
其中,bij'是与集中质量m,线弹簧k1、k2扭转弹簧kT1、kT2及特征值有关的项,式(12)即为含有集中质量的固有频率特征值的通用表达式。带入各边界参数值即可求出特征值(此处,再将特征值带入式(10)即可求得振型函数。
2 遗传算法简介
遗传算法[8-9]是由美国Michigan大学的John Holland教授在20世纪60年代提出的,它是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。现在已广泛应用到了函数优化,组合优化,图像处理等诸多领域。
遗传算法与传统搜索算法不同,它以适应度函数为依据,通过对种群中的所有个体实施遗传操作,实现群体内个体结构重组的迭代过程随机搜索算法。选择、杂交、变异构成遗传算法的三个主要遗传操作因子。其主要计算步骤如下:
①选择一定数目的个体构成初始种群,并求出种群内各个个体对应的适应度函数值。
②计算选择函数的值:根据适应度函数的优劣,通过概率从种群中选择若干个个体。遗传算法工具箱中提供了几个选择函数:轮盘选择算法、归一化几何选择方法等。
③通过染色体个体基因的复制、交叉、变异等创造新的个体,构成新的种群。
④进行循环,若终止条件不满足,则转到步骤②。否则跳出循环,输出参数值。
应用遗传算法来识别结构的边界条件,实际上就是将参数辨识问题转化为一个数值优化问题,再利用遗传算法的全局优化能力进行优化,从而得到待识别参数的全局最优值。
3 遗传算法识别结果
本文利用英国谢菲尔德大学开发的遗传算法工具箱,联合MATLAB编程,对两端有轴承支承,中间附带工作台的机床进给系统进行了识别,机床主轴实际参数如表1所示。
①本文所需要识别的边界条件有五个:丝杠两端的线支承弹簧k1、k2、kT1、kT2以及工作台的质量大小m。
②目标函数。根据初始种群中各边界条件的值计算出的主轴丝杠的前n阶固有频率固有频率,和前n阶(本文中n=3)固有频率实测频率,建立优化目标函数:
A=,
③适应度函数。计算频率和实测频率越近越好,本文的适应度函数设置为:G=。
④遗传和收敛。选择、交叉、变异分别选用轮盘赌选择、单点交叉和均匀变异,这也是遗传算法中最常用的方法。设置进化代数终止遗传操作,进化代数设置为100代,识别结果在前50代就收敛了。机床主轴的主要参数见表1。
识别得到的主轴边界条件见表2:
根据识别边界条件结果计算得到机床主轴的前3阶固有频率与实际频率。
通过分析计算值与实验值,可以看出两者差距不是很大,都在3%以内,说明边界参数识别的正确性。
4 结 语
本文推导了梁结构的动力学方程,得到了其频率方程和振型,提出了基于遗传算法的机床主轴边界条件识别方法,以试验模态结果与计算固有频率差值最小为优化目标函数,对丝杠主轴的边界支承刚度及工作台质量进行了识别,识别结果验证了本方法的有效性,具有一定的工程实用性,为机床进给系统的设计制造提供了一定的依据。
参考文献:
[1] 张义民.机械振动[M].北京:清华大学出版社,2007.
[2] 清华大学工程力学系.机械振动(上册)[M].北京:机械工业出版社,1980.
[3] 钟一锷,何衍宗.转子动力学[M].北京:清华大学出版社,1990.
[4] 张会端,谭庆昌.机床进给系统的动力学分析[D].长春:吉林大学,2009.
[5] Cheng CC,Lin JK.Modeling a rotating shaft subjected to a highspeed moving force[J].Jounal of Sound and Vibration,2003,(26).
[6] 朱坚民,张统超.基于改进自适应遗传算法的固定结合面动态特性参数优化识别[J].中国机械工程,2014,(3).
[7] 应光耀,郑水英,刘淑莲.遗传算法在转子轴承系统参数识别中的应用[J].机械强度,2004,(1).
[8] Chou J H,Ghaboussi J,Genetic algorithm in structural damage detection[J].Computers&Structures.2001,(14).
[9] 雷英杰,张善文.MATLAB遗传算法工具箱及应用(第二版)[M].西安电子科技大学出版社,2014.

