基于迭代优化度与直线搜索的改进粒子群算法

王斌

摘要：现有粒子群算法无论是在算法运行的前期还是后期，现有的改进方法都是以适应度值来作为评价粒子优劣的唯一标准，本文根据挖掘有潜力粒子的思想，提出迭代优化度概念来刻画粒子的潜力，并对于潜力较大的粒子采用直线搜索的策略来进行搜索，这样就避免所有的粒子均参考适应度值优秀的粒子运动，提高了算法效率，保持了潜力大的粒子的独立性。将改进粒子群算法用2个经典的检验函数进行对比检验，结果表明提出的改进粒子群算法能大幅度增强摆脱局部最优解的能力，有效地改善寻优性能。

关键词：PSO算法；改进PSO算法

1.引言

粒子群算法是基于个体有序运动的群体智能算法，是由Eberhart和Kennedy[1][2]在1995年提出来的。但是标准的PSO算法主要存在早熟和寻优精度低的问题，因此为了实现加快收敛速度和避免陷入局部最优解，改进的粒子群算法被提出。

现有的改进方式主要有改进算法参数、改进搜索方式和改进搜索领域的拓扑结构[4]，然而到目前为止同时兼顾收敛速度和跳出局部最优解的能力是很难的。比如，文献[3]把重心放在避免陷入局部最优解的问题上，却带来了收敛速度的变缓。2002年Clerc[5]等引入了收缩因子，提出了一种自适应PSO算法，到目前为止参数的自适应策略都是以种群迭代次数为参考变量的。2013年何茜[6]提出一种删除机制，对于长期不更新的粒子，直接删除。

2.粒子群算法简介

2.1粒子群优化算法

粒子群优化（particle swarm optimizer，简称PSO）算法是模仿鸟类群体智能行为而提出的算法，其实施过程：在算法开始时，对各粒子赋予初始值（初始速度和初始位置），初始种群在N维解空间中为均匀分布。其中第i个粒子在研究区域中所处的位置和速度分别表示为Xi=（xi1，xi2…，xin）和Vi=（vi1，vi2…，vin），根据迭代原则找到最优解。在每次迭代时，粒子通过跟踪两个极值来更新自身的速度和位置，一个极值是粒子本身到目前为止所找到的最优解，这个极值称为个体极值，设为Pbesti=（Pbesti1，Pbesti2…，Pbestin）；另一个极值是该粒子的领域到目前为止找到的最优解，这个极值称为整个领域的最优极值，设为Nbesti=（Nbesti1，Nbesti2…，Nbestin）。第i个粒子是根据以下公式（1）（2）（3）更新自身的速度和位置：

Vi=ωVi+c1×rand×（Nbesti-Xi）+c2×rand（）×（Pbesti-Xi）Xi=Xi+Vi

ω=（ω1-ω2）Imax-IImax+ω2

式中c1和c2是加速常量，rand是[0，1]之间的随机数，ω1、ω2为惯性权重的初始值和终值，I为当前迭代次数，Imax为最大迭代次数。

3.粒子群优化算法的改进

3.1迭代优化度与直线搜索

现有的改进方法均采用将适应度值好坏作为评价粒子优劣的唯一标准，对于适应度值暂时不优秀的粒子，强制性地让其以暂时优秀的粒子为中心运动，这样不仅会让种群失去多样性，而且还会造成潜在的优秀粒子被忽略。因此，在粒子群算法中，应该给予那些进步程度大的潜在优秀粒子独立发展的空间，这样就有更大的可能发现更优秀的粒子。

现有的改进方法无一例外都存在一个严重的问题，那就是将适应度值好坏作为评价粒子优劣的唯一标准，对于那些适应度值暂时不优秀的粒子，很粗暴地让它们以暂时优秀的粒子为中心运动，这样不仅会让种群失去多样性，而且还会失去很多寻找到更加优秀粒子的机会。

基于以上的分析，本文提出迭代优化度的概念来刻画粒子的进步程度，对于求最小值的优化问题，定义如下：

D_betteri，t=fiti，t-1-fiti，tfiti，t-1×100%（4）其中，i表示粒子的编号，t表示迭代种群迭代次数，fiti，t适应度值，D_betteri，t迭代优化度。

最后，考虑对于迭代优化度较大的粒子的独立搜索，但是考虑到算法的复杂度，必须提出一种简单有效的搜索方式。在此，本文提出了直线搜索的策略，对于迭代优化度排名靠前的粒子进行沿着原来速度所对应方向的直线搜索，在直线上有序取点进行搜索。

4.性能测试分析

为了测试算法的性能，选择2个标准的测试函数用于优化实验，2个函数的函数表达式、搜索空间、理论全局最小是入表1所示。

表1标准的测试函数

函数函数表达式搜索空间最优解

Rosenbrockf2（x）=∑ni=1100（xi+1-x2i）2+（1-xi）2[-100，100]0

Griewankf4（x）=14000∑ni=1x2i-∏ni=1cos（xii）+1[-100，100]0

通过比较测试函数的平均适应度值、方差适应度值、最优适应度值和最差适应度值的方式对三种算法进行评价，其中平均适应度值和方差适应度值用于评价算法的寻优精度和鲁棒性。下面将通过与文献[22]中所提出的引入删除机制的粒子群算法作对比，来说明本文引入迭代优化度与线性搜索策略的粒子群算法的性能。

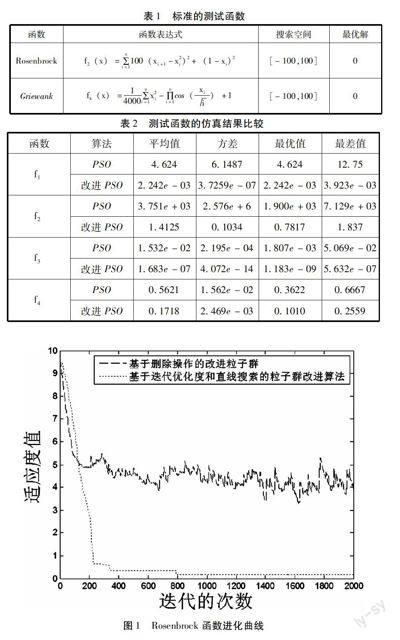
算法参数设置如下：测试函数的维数为10，迭代次数为2000次。种群规模为100，C1=C2=2.0，惯性权重w1=w2=0.8，适应度值选优比例Rate_better=0.1，迭代优化度选优比例Rate_imp=0.1。结果如表2所示，其曲线如图1—图2所示。

表2測试函数的仿真结果比较

函数算法平均值方差最优值最差值

f1

PSO4.6246.14874.62412.75

改进PSO2.242e-033.7259e-072.242e-033.923e-03

f2

PSO3.751e+032.576e+61.900e+037.129e+03

改进PSO1.41250.10340.78171.837

f3

PSO1.532e-022.195e-041.807e-035.069e-02

改进PSO1.683e-074.072e-141.183e-095.632e-07

f4

PSO0.56211.562e-020.36220.6667

改进PSO0.17182.469e-030.10100.2559