潜器耐压壳体圆度测量方法设计
邱磊 龙宇飞

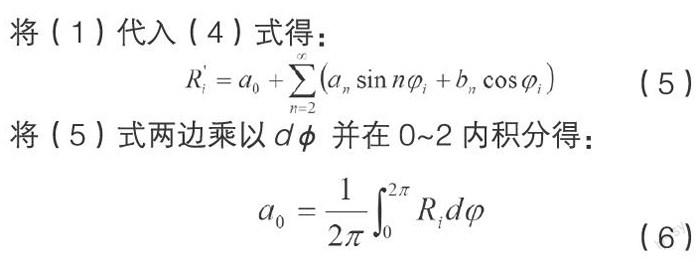
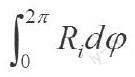
摘要:针对潜器耐压壳体圆度测量中撑杆法测量的弊端,本文基于激光测量技术,设计了潜器耐压壳体圆度测量系统,并重点分析了该系统的测量方法及测量误差,结果表明,该系统在保证测量准确性的基础上,测量过程较撑杆法更快捷,数据更直观,数据处理更简便。
关键词:潜器;圆度测量;激光测量
潜器耐压壳体圆度是保证船体总体稳定性及深潜安全性的核心,因此潜器的圆度测量是潜器建造中一项必不可少的重要工艺环节。目前,潜器耐压壳体圆度测量的主要方式是测量耐压壳体的肋骨沿半径方向对纯圆的偏差,即肋骨的初挠度。肋骨初挠度的测量,通常是将圆周分成16或32等分,采用撑杆法测出每个测点到圆心的半径,再与理论半径值相比较。便可得出径向偏差值。
但是,从实船建造实践中发现,撑杆法测量需消耗大量人力,且测量精度低,人为误差大,易受环境影响,测量数据的离散度较大。统计发现。撑杆测量方法存在约至少2mm的人为误差。
随着激光测量技术的发展,高精度、高效率的激光测量方法大量应用于建筑和船舶等行业,同时该方法可以方便地得到大量的连续测量值,并方便开展数据的即时分析和后续采集处理。因此设计并使用基于激光测量技术的潜器耐压壳体圆度测量系统的意义重大。
1潜器耐压壳体圆度测量系统的组成
耐压壳体圆度测量系统由激光跟踪仪、光标靶、数据存储设备、数据分析显示设备(包括分析软件)和固定支承与调节部分等组成。系统框图如图1所示。
激光跟踪仪是耐压壳体圆度测量系统的核心部分,主要作用是发射和接收激光。并对距离进行测量。光标靶作用是贴在被测点的表面。对激光进行反射,利用凹面聚光的原理,使入射的激光按原方向反回。固定支承与调节部分,潜器圆度测量系统在使用时要求安装基础稳定,同时调节激光跟踪仪在水平、垂直方向平移及锁紧,调节激光跟踪仪在水平和俯仰的角度并锁紧。数据存储和分析显示设备是实现测量的圆度数据实时存储、分析及显示,内附数据分析软件,实现圆度的实时分析计算。
2基本原理
利用激光测距的原理,基本可以归结为测量光往返目标所需要的时间,然后通过光速和大气折射系数计算出距离。由于直接测量时间比较困难,通常是测定连续波的相位,当然测相也不是直接测量激光的相位,而是测量调制在激光上面的信号相位,通过相位变化计算出时间的变化,从而得到激光往返目标的时间。
被测物体的平面必须与光线垂直,本测试系统使用的是一种新型光标靶,将光标靶贴在被测点上,利用光标靶对入射激光进行反射。光标靶是采用有机玻璃制成的,靶体的后面是永磁铁,可以方便的吸附在壳体上,光标靶正面采用特殊的凹面设计,只要激光入射至光靶中心,就可以保证光可以反射回入射的方向。
3测量方法
测试过程分为四步:第一步,单站测量;第二步,转站测量;第三步,全点拟合;第四步,数据有效性判定。
3.1单站测量
是指在无内部结构妨碍的情况下,激光跟踪仪一次定位后,可测量所有肋位全部数据。测试方法如下图所示。
在某一固定测量站,以耐压壳圈的轴向为z轴方向,以横向为x轴方向,以竖直方向为Y轴方向,测出各点的三维空间坐标(Xi,Yi,Zi),这些点都是以O点为原点。
3.2转站测量
耐压壳体内部有平台、隔壁等结构时,激光无法穿过,必须采用移动测量仪器的方式进行其它点的测量,然后再进行圆度拟合,这种测量方式称之为“转站”测量,简单说转站测量就是激光跟踪仪移动位置测量的一种方法。如下图所示。
转站前,A点在以O为原点的坐标系下的坐标是(Xi,Yi,Zi),转站后以O1为原点的坐标系下的坐标是(X11,Y11,Z11),B点以O1为原点的坐标系下的坐标是(X12,Y12,Z12),转化为以O为原点的坐标系下的坐标是[X12+(X11-Xi),Y12+(Y11-yi),Z12+(Z11-Zi)].以此类推,转站后以O1为原点测量的数据要转化为以O为原点的数据。
基于矩阵转换的方法,通过对矩阵方程进行数值求解,确定转站前后坐标转换矩阵,可以实现高精度的转站测量,但前提是两站测量时要有6个公共测点,若无法满足时,也可采垂直轴不变的转站方式,此种方法只需2个公共测点。
为验证转站测量的可靠性,选取模型进行圆度测量,将模型圆周分为32等分点,一种是在不转站的情况下进行测量,另一种是先测量上面16个点,然后转站测量下面16个点,通过两种方法测量结果进行比较,随机抽取10个点的初挠度结果,如表1所示。
从表中可以看出,转站测量与不转站测量的精度相当,两者相差1mm以内,证明转站测量的精度可以满足测量的要求。
3.3全点拟合
以耐压壳圈的轴向为z轴方向,以横向为x轴方向,以竖直方向为Y轴方向。将所有测点转化到此坐标系下。同一Z值点作为同一站号,将每一肋骨站内的测点Xi、Yi值转化为半径R,即。
肋骨初挠度从理论上来说应该指实际柱面与理论圆柱面形状之差。由于测量工艺上的困难,因此。工程上都以一个肋骨的实际曲线与正确圆形之差作为初挠度。
现取一个肋骨断面,并任选一点O点作为圆心,并使O点尽量接近肋骨真正的圆心。因此。肋骨的实际形状以O为原点用极坐标来表示可以写成下式:
由于求取初挠度必须知道相对于真正圆心上的半径R'与正确圆形半径之差,因此还必须研究R与R'之间的关系。
设测量中心为O点,“真正”的圆心在O'点,
考虑测量中心与真正圆心偏离不大,故可略去并展开(3)式则得:
将(1)代入(4)式得:
将(5)式两边乘以dφ并在0~2内积分得:
因为表示肋骨周长,因此,α0就是肋骨正确圆形的实际半径(平均值)。
因此,初挠度为:
将(4)式代入(7)式即得适用于实际的初挠度的计算公式,即
求解肋骨径向初挠度按以下公式计算:
式中:
Wi为肋骨径向初挠度。外凸为iE;
φi为在每一肋骨圈内测点与起始点所对应的夹角;
Ri为圆周上各点距测量中心的距离;
r为理论半径:
利用傅里叶变换得:
运用以上计算方法,编制系统分析软件作为数据处理程序。软件界面见图3。
3.4数据有效性判定
由于采用该计算方法的前提是同一肋骨站拟合面Z坐标一致。因此以Z轴方向数据作为有效性判定的依据,即同一肋骨站内所有测点的Z值应满足一定的公差要求,否则认为此批测量数据无效,重新进行测量。
4误差分析
4.1仪器的回转精度引起的误差
回转的轴线在回转过程中,对轴线平均位置的相对位移即为回转误差运动。误差运动使回转轴在每一瞬时发生轴向窜动和径向跳动,使得同一圆周内不同测点不全在一个模截面内,从而使各采样点间的相关性降低。但是,由于轴向窜动一般很小,而实际被测面是光滑的,测头在被测面采样时,也不可能是纯粹的点接触,而是小面积接触,因此轴向窜动对测量精度的影响可以忽略。
径向跳动误差将直接传递到采样数据中,进面影响计算精度。因此,径向回转精度是圆度测量中极为重要的精度指标。
4.2偏心引起的误差
由于测量时的回转中心与理论圆的圆心不重合,存在偏心而引起计算的误差。由下面公式可知:
考虑测量中心与真正圆心偏离不大,故可略去并展开。若假设,32等分点,
则
若按此方法,忽略二次方项,则,而假设wi=R't-a0,则Wi相132mm;
当时,则Wi相0.08mm。因此,此种方法必须使测量中心与真正圆尽量接近,偏差10mm不会对测量结果有影响。
4.3测点数对测量误差的影响
由于在轮廓上实测有限数量的点来代替被测试及轮廓的全貌,在原理上就存在了误差。为了减少此误差,应合理选择测点数。用计算机对圆度谐波进行模拟,利用数值积分可以求出对应于一定谐波时各种测点的不确定度,随测点数增加,测量不确定度下降。
5结论
(1)本系统测量过程较撑杆法更快捷,数据更直观,数据处理更简便。
(2)转站测量的精度可以满足测量的要求。
(3)测量时,选定圆心应尽量接近肋骨站真正的圆心。
(4)同一肋骨站内所有测点的Z值应满足一定的公差要求,否则测量数据误差较大。
(5)轴向窜动对测量精度的影响可以忽略,但径向回转精度是圆度测量中必须重点考虑的精度指标。
(6)测量的不确定度与测点数量呈反比。

