水下维修载人潜器运动仿真
朱晓环,刘 峰,张定国,韩端锋,彭小佳
(1.海洋石油工程股份有限公司,天津 300456;2.哈尔滨工程大学,哈尔滨 150001)
水下维修载人潜器运动仿真
朱晓环1,刘 峰2,张定国1,韩端锋2,彭小佳1
(1.海洋石油工程股份有限公司,天津 300456;2.哈尔滨工程大学,哈尔滨 150001)
操纵性是载人潜器的重要性能,通过载人潜器的运动仿真可以对于载人潜器的操纵性进行评估,本文以水下维修载人潜器为研究对象,建立了载人潜器空间六自由空间运动数学模型的基础上,利用Matlab的S-function建立了基于Simulink的载人潜器控件运动仿真系统,进行了载人潜器运动仿真,为运动控制系统设计提供了重要依据。
水下维修载人潜器;六自由度;数学模型;运动仿真
0 引言
载人潜器可以携带海洋科学家、工程技术人员进入海洋深处,是人类实现开发深海、利用海洋的一项重要技术手段[1]。水下维修载人潜器是载人潜器的一种,主要应用于水下生产设施的维修、事故处理、日常巡检等,是水下生产设施安全生产的重要保证。水下维修载人潜器在水下执行作业任务时要求其能够对于复杂海底地形进行灵活的机动、正确到位等,这些均与载人潜器的操纵性能密切相关[2]。
载人潜器在水中运动时,是具有6个自由度的运动刚体,是一个强耦合的非线性系统,同时复杂的海洋环境导致获得水下潜器的精确模型非常困难[3]。计算机仿真在计算机上建立仿真模型,模仿实际系统的运行状态及其随时间的变化过程。通过对仿真试验过程的观察和统计,得到被仿真系统的仿真输出参数和基本特性,以此来估计和推断实际系统的真实参数和真实性能,为一些复杂系统创造了计算机试验环境,使系统的性能和长期的动态特性能在极短的时间内由计算机得到全面的实现[4]。载人潜器运动仿真的研究需要解决的问题是针对载人潜器操纵性能进行预报,运动仿真通过计算机数值模拟的方法研究载人潜器的空间运动特性,是一种科学有效、省时、省力的研究方法[5,6]。随着载人潜器的发展,对其机动性、控制品质及导引精度的要求也就变得更加严格。简化模型和以往所采用的分析方法已远不能满足载人潜器研究、设计的需要。Matlab仿真工具箱Simulink的出现为解决上述问题提供了便利的仿真环境[7]。
首先针对水下维修载人潜器的空间运动方程进行研究,建立了基于Matlab/Simulink的水下维修载人潜器运动仿真系统,利用该仿真系统对于水下维修载人潜器几个典型运动状态进行了仿真,得到了相关结论,为水下维修载人潜器的控制系统设计提供了理论依据。
1 载人潜器空间运动方程
为了描述水下潜器的运动以及建立仿真系统,必须首先建立适合描述水下潜器运动的坐标系。根据国际水池会议(ITTC)推荐的和造船与轮机工程学会(SNAME)术语公报的体系,坐标系是下列两种右手系:一个是固定坐标系E-ξηζ 固定于地球,称为“定系”;另一个是运动坐标系G-xyz,固定于潜器,随潜器一起运动,称为“动系”,具体如图1所示。
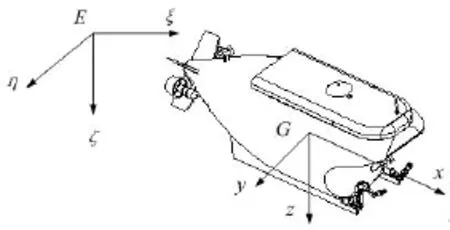
图1 固定坐标系和运动坐标系
图1中,定系E-ξηζ:原点E可选地球上某一点,如海面或海中任一点,Eξ的轴位于水平面,并以潜器的主航向为正向;Eη轴位于Eξ轴所在的水平面,按右手法则将Eξ轴顺时针旋转90度即是;Eζ位于ξEη坐标平面,指向地心为正,动系G-xyz:原点G选在潜器的任一点,Gx轴、Gy轴和Gz轴,分别经过G点的水线面、横剖面和纵中剖面的交线,正向按右手系的规定,即Gx轴指向艇首为正、Gy轴向右为正、Gz轴向下为正,Gx轴、Gy轴和Gz是潜器的惯性主轴。
根据刚体运动学理论,载人潜器空间六自由度运动的方程为[8,9]
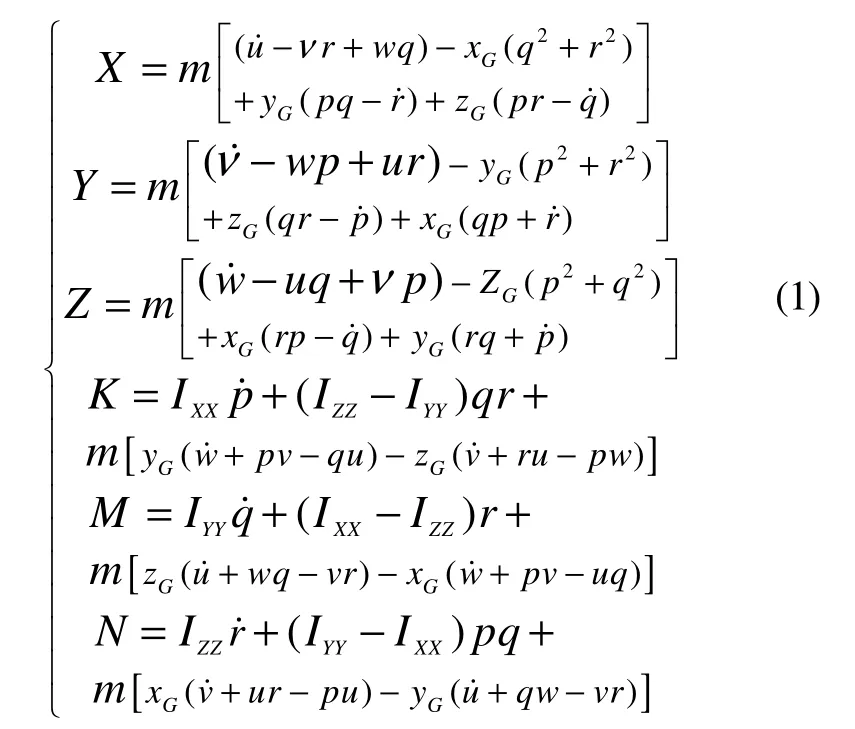
式中,m为潜器质量;Ixx、Iyy、Izz为潜器质量m对Ox、Oy、Oz、轴的转动惯量;u、v、w、p、q、r六个自由度的(角)速度;六个自由度的(角)加速度;X、Y、Z、K、M、N表示作用在潜器上的的作用力(矩)。
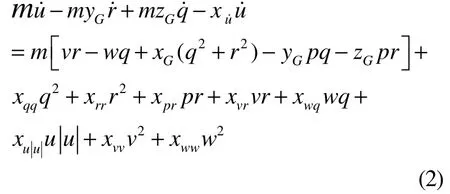
右端非惯性水动力可以表示为:

2 载人潜器受力分析
2.1 重力和浮力
作用在载人潜器上的重力包括P全排水量P0和各种载荷的变化ΔP。P0的作用点为重心G(XG,YG,ZG),ΔP指相对于P0的增减,每一项变化都有一个重心Gj。
作用在载人潜器上的浮力B包括全容积浮力B0和浮力的各种变化ΔB,浮力的作用点为浮心C(XC,YC,ZC),ΔB指相对于B0的增减,则艇体坐标系下的重力与浮力在各坐标轴上作用的分量为:
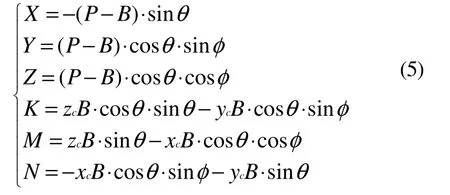
2.2 推进器推力
目标载人潜器推进系统采用导管推进器,在潜器中部两侧布置垂推两部,垂推可旋转至水平位置兼作主推功能;主推两部布置于尾部,在艏艉各布置一部推进器以实现载人潜器的转艏运动,必要情况下可进行横移运动。
图2中,lMTy为主推距中线横向距离;lVTy为垂推距中线横向距离;lALTx为尾侧推距中心纵向距离;lFLTx为首侧推距中心纵向距离;lVTx为垂推距中心纵向距离;lALTz为尾侧推距中心垂向距离;lFLTz为首侧推距中心垂向距离。
对于导管推进器而言,可将推进器推力(矩)表达成航速V,和推进器控制电压ut函数的形式[10]。

将推进器敞水试验测得的电压和航速的推力(矩)拟合为曲线,就可通过曲线插值的得到不同航速和控制电压下的推力(矩),以主推为例,敞水条件下,水流速度分别为0 m/s、0.5 m/s、1 m/s、1.5 m/s、1.8 m/s,控制电压取值范围为-5 V~5 V,图3为主推敞水试验曲线。

图2 推进器布局
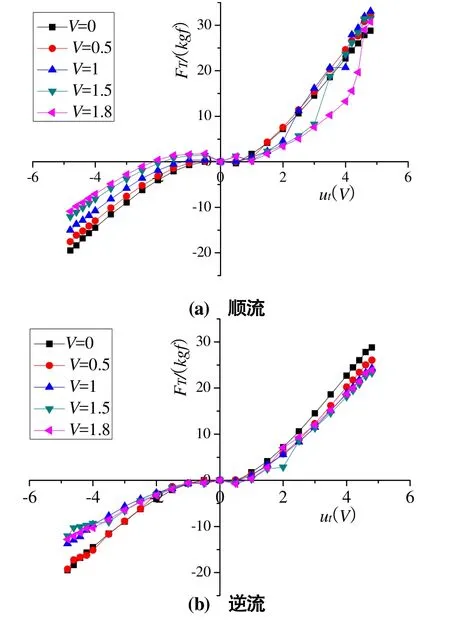
图3 主推敞水试验曲线
2.3环境干扰力
载人潜器的运动要受到环境扰动的影响,包括风、波浪和海流等,其中对潜器的运动影响最大的是波浪和海流。根据线性波浪理论,当潜器的航行深度达到一定深度范围后,就可以认为其已经不受到波浪力的作用,此时,环境干扰力只考虑海流因素。
载人潜器在海流中的艇体水动力是载人潜器相对于海流的相对速度ur、vr、wr和相对加速度的函数,相对流速通过式(6)求得:
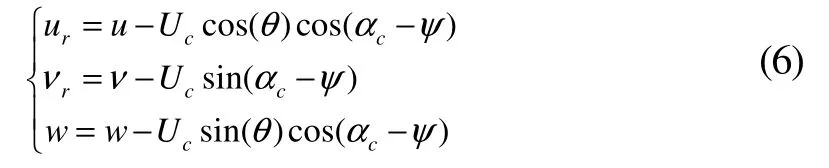
式中,Uc为流速;αc为流向角;ψ为艏向角。
对时间微分后可得到相对加速度为
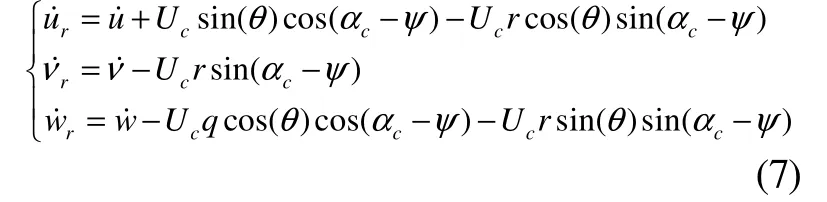
将得到的相对加速度代到六自由度运动方程后,就可得到所求的仿真系统运动模型。
3 Simulink仿真模型的构建
3.1 模型初始化
在首次仿真循环开始之前,Simulink会初始化S-function,在该阶段期间,Simulink会执行以下任务:初始化SimStruct,这是一个仿真数据结构,包含了关于S-function的信息;设置输入和输出端口的数量和宽度;设置块的采样时间w分配存贮区间和参数sizes的阵列。
根据载人潜器运动数学模型,共设置12个连续状态量及输出量:u、v、w、p、q、r、ξ、η、ζ、ϕ、ψ、θ;设置20个输入量:u0、v0、w0、p0、q0、r0、ξ0、η0、ζ0、ϕ0、ψ0、θ0、Uc、αc、六个推进器控制电压。
在S-function的初始化子程序中为了给Simulink提供输入、输出、状态的数量,以及其它特性信息,必须在mdlInitializeSizes的开头调用simsizes,需要进行如下设置:
function[sys,x0,str,ts]=mdlInitializeSizes(V0)
sizes=simsizes;
sizes.NumContStates=12;%连续状态个数。
sizes.NumDiscStates=0;运动模型中无离散状态变量。
sizes.NumOutputs=12;输出个数。
sizes.NumInputs =20;输入个数。
sizes.DirFeedthrough=0;同一时刻的输入值时为1;否则为0。
sizes.NumSampleTimes=1;采样时间的个数,每个系统至少有一个采样时间。
sys=simsizes(sizes);%返回以上结构参数。
str=[ ];%保留以后使用。
ts=[0 0];%对连续系统,采样时间为0。
3.2 计算状态微分
Simulink模型以flag=1的语句调用S-Function时,将转至子函数function sys=mdlDerivatives(t,x,u)计算状态的微分。计算状态微分子函数的简略设计步骤如下:
1)给参数赋值:包括载人潜器六自由度运动方程中运用到的所有的特征参数、海水密度、无因次水动力系数等;
2)根据变换得到的载人潜器的六个自由度运动方程的矩阵形式,求出所需的系数矩阵E;
3)写出输入矩阵u,即各推进器所产生的力以及力矩;
4)求得载人潜器在各自由度上除惯性水动力以外的合力;
5)列出载人潜器运动方程的矩阵形式,进而求出连续状态变量的微分值;
6)列出计算位置、姿态六个连续变量的辅助方程式;
7)将计算的各个微分组合成向量,赋予返回变量sys,作为子函数的输出,该输出即为模型状态的微分。
3.3 模型输出
当flag=3时,S-Function调用子函数function sys=mdlOutputs(t,x,u)计算模型的输出。因已将模型的状态向量x设计为模型的输出,因此只要在子函数mdlOutputs中将状态向量x赋予返回变量sys。
3.4 计算下一个采样时间
当flag=4时,S-Function调用function sys=mdlGetTimeOfNextVarHit(t,x,u)子函数,将下一次采样时刻的值则赋给返回变量sys。只有在采样时刻为可变时,S函数才会以flag=4的条件被调用。
3.5 仿真终止
当仿真以某种原因结束时,S函数将以flag=9被调用S函数此时需要完成一些终止仿真的任务,这一步骤不需赋值给sys。
在完成以上步骤后,S-function编程结束,并以文件名HOV-motion.m存盘。
3.6 基于Simulink的载人潜器运动仿真系统
本文的载人潜器运动仿真系统采用Simulink进行构建,载人潜器运动仿真原理见图4,图4的仿真系统由三部分组成:
1)输入模块:载人潜器初始速度、初始位置、海流、推进器电压(6部推进器);
2)运动计算模块:利用已经编写完成的S函数创建Simulink中的S-Function模块,S-Function主要进行载人潜器空间运动方程的解算;
3)输出模块:进行载人潜器运动的实时模拟,可进行实时速度、实时位置的输出与显示。

图4 载人潜器运动仿真原理
4 仿真系统的实现
为考核载人潜器的运动能力,本文将载人潜器仿真分为三种模式:
1)最大航行能力考核:左右主推控制电压5 V;左右主推控制电压5 V、左、右垂推控制电压5 V;艏艉侧推控制电压5V;左右垂推控制电压5 V,以上四种情况其他初始变量设置均为0;
2)水平面回转能力考核:左右主推控制电压5 V、艏艉侧推控制电压5 V;左右主推控制电压5 V、艏艉侧推控制电压5 V、左右垂推控制电压5 V,以上两种情况其他初始变量设置均为0,两种情况下在ψ=±10°情况下,侧推就反转,共运动5个周期;
3)空间回转运动考核:θ=5°、左右主推控制电压5 V、艏艉侧推控制电压5 V;θ=5°、左右主推控制电压5 V、艏艉侧推控制电压5 V、左右垂推控制电压5 V,以上两种情况其他初始变量设置均为0,运动时间为1 500 s。三种仿真模式得到的仿真结果见图5~图7。

图5 最大航行速度仿真
图5可以看出,主推和垂推共同作用下载人潜器航速可达到1.51 m/s,主推单独作用下载人潜器航速可达到1.36 m/s,侧推作用下的载人潜器横移最大速度为0.463 m/s,垂推作用下的载人潜器升沉最大速度为0.380 m/s。
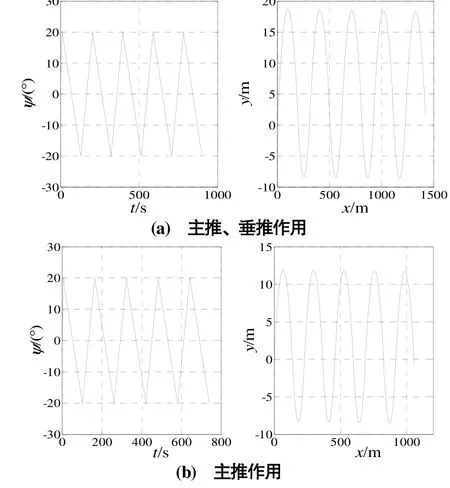
图6 Z形机动仿真
图6可以看出,在主推和垂推共同作用下,载人潜器运动周期199.3 s、侧向运动幅度为18.8 m、主方向前进距离308.2 m;在主推作用下,载人潜器运动周期162.6 s、侧向运动幅度为11.85 m、主方向前进距离224.9 m。
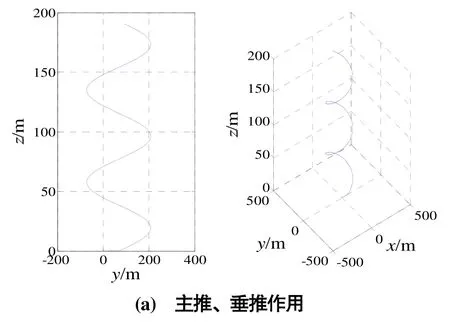

图7 空间回转运动仿真
图7可以看出,在主推和垂推共同作用下,1 500 s内载人潜器垂向运动距离为190.6 m、回转直径280.0 m、每个周期垂向运动距离77.9 m;在主推作用下,1 500 s内载人潜器垂向运动距离为171.6 m、回转直径204.8 m、每个周期垂向运动距离55.4 m。
5 结论
本文针对水下维修载人潜器的运动仿真系统的研究,通过系列典型运动状态的仿真,得到以下结论:
1)进退方向采用主推与垂推共同作用下的航速比主推单独作用下的航速略大,由于载人潜器所携带的能源有限,为节约能源,在巡航速度建议采用主推完成进退方面的运动,紧急情况下可采用主推与垂推共同作用模式;
2)横移速度和升沉速度都不是很大,水平运动时采用侧推转首,再利用主推作用完成横向运动,以弥补横移速度的不足;下潜状态优先考虑采用重力式下潜模式,也可采用纵倾式航行;
3)转首运动及空间运动时,为节约系统能源,优先考虑主推完成,特殊情况采用主推和垂推共同作用模式。
[1]汤国伟,邱中梁,王璇.深海载人潜水器压载水箱注排水系统研究[J].液压与气动,2008(3):7-9.
[2]谢俊元.深海载人潜水器动力学建模研究及操纵模拟器研制[D].江南大学博士学位论文.2009.
[3]刘小峰.海洋探测机器人操纵性及运动仿真研究[D].哈尔滨工程大学硕士学位论文.2007.
[4]韩晓宝,高维杰,刘海强.船舶旋回运动的建模与仿真[J].中国水运.2007,8(5):22-24.
[5]A.Alan,B.Pritsker.Compilation of Definition of Simulation[J].Simulation Transactions of the Society for Modeling & Simulation International,1979,33(2):61-63.
[6]谢俊元.一种虚拟现实的深潜器运动仿真系统[J].船舶力学.2005,9(4):53-61.
[7]潘瑛,徐德民.自主式水下航行器空间运动矢量建模与仿真[J].系统仿真学报.2003,15(4):538-539.
[8]杨新平,徐鹏飞,胡震.深海机器人视景仿真系统研究[J].海洋工程.2012,30(1):137-144.
[9]谢俊元,马岭,胡震.载人潜器运动操纵模拟[J].中国造船.2006,47(2):62-69.
[10]王波.微小型水下机器人运动仿真研究[D].哈尔滨工程大学硕士学位论文.2008.
Motion Simulation of Underwater Repair HOV
Zhu Xiao-huan1,Liu Feng2,Zhang Ding-guo1,Han Duan-feng2,Peng Xiao-jia1
(1.Offshore Oil Engineering CO.,Ltd.,Tianjin 300456,China; 2.College of Shipbuilding Engineering,Haerbin Engineering University,Harbin 150001,China)
Maneuverability is an important property of HOV (Human Occupied Vehicle).The HOV motion simulation for underwater repair HOV can give assessment to maneuverability.Taking underwater repair HOV as a research object,based on establishing HOV space six free degree space motion mathematical model,the Matlab S-function is used to construct the control motion simulation system for HOV.The motion simulation is carried out,which provides important basis for the design of motion control system.
underwater repair HOV; six free degree; mathematical model; motion simulation
U661.4
A DOI:10.14141/j.31-1981.2016.05.005
大型油气田及煤层气开发项目27,子课题五“深水水下应急维修装备与技术”,课题编号:2011ZX05027-005。
朱晓环(1967—),女,高级工程师,研究方向:船舶与海洋工程仿真。

