蛟龙号载人潜水器无动力潜浮运动分析系统开发
潘彬彬,崔维成,叶 聪,刘正元
(中国船舶科学研究中心,江苏 无锡 214082)
1 引 言
基于气球原理设计的第一代和第二代载人潜水器,均是采用无动力下潜和上浮的方式[1-3]。这样做获得的最大好处就是可以大大地节省潜水器上的能源,但需要解决无动力潜浮过程中的水动力学问
题[4]。
在“蛟龙”号设计阶段,刘正元等就开始研究载人潜水器的无动力下潜上浮运动[5-6],给出了一套简化分析方法并应用于“蛟龙”号载人潜水器的无动力潜浮设计。为了更精确和方便地进行海试和今后应用下潜的配载,我们在“蛟龙”号载人潜水器3 000米级海试数据的基础上,曾经建立了一个理论上更为精细的载人潜器无动力上浮下潜运动模型,并根据该模型开发了一个运动分析系统[7],用于预报“蛟龙”号5 000米级海试的配载和速度。但是由于3 000米海试所有潜次的海试数据中都存在开动推进器和调节压载水舱的操作,没有真正意义上的无动力上浮下潜数据用于标定模型参数,因此,所建立的无动力潜浮运动分析系统并不十分可靠。在2011年7-8月间进行的5 000米级海试过程中发现该模型预报值比实际值偏大了约80kg。在这次的5 000米级海试中,D44潜次首次实现了全程无动力上浮下潜运动,为改进载人潜器无动力上浮下潜运动模型提供了宝贵的数据。本文将对D44潜次的数据进行分析,在此基础上改进潜器无动力上浮下潜运动模型,期望开发出真正可靠的“蛟龙”号载人潜水器的无动力潜浮运动分析系统,为2012年的7 000米级海试以及今后的应用提供可靠的手段,同时,本文所建立的精细分析方法也可以应用于我国正在进行的4 500米载人潜器无动力潜浮运动的设计。
2 载人潜水器无动力潜浮运动模型
在文献[7]中详细给出了载人潜水器的无动力潜浮运动分析精细模型,在该模型中,认为无动力潜浮运动过程中潜器所受的外力只有重力W、浮力B及流体阻力Fd。此外考虑到稳态运动时其角速度为零等因素,模型建立在固定坐标系内,如下图1所示。
潜器在固定坐标系中oz0方向的力平衡方程为:

其中M=潜器的质量与z0方向附加质量之和;0=潜器垂向(z0方向)加速度;W=重力;B=浮力;Fd=潜器在铅垂方向运动时受到的 (z0方向)的阻力。潜器无动力下潜上浮的大部分时间中潜器的运动可以近似为平稳运动,即近似认为平稳阶段潜器的加速度为零:

图1 坐标系Fig.1 Coordinate system

但(2)式中各部分力与文献[7]中的模型有所变化,所以本文将对每个部分力重新介绍。
2.1 阻力项Fd
如图1所示,潜器运动时存在一定的纵倾角θ,文献[6]推导了潜器速度方向(攻角)α和纵倾角θ的关系为:

其中:Cx(α)为潜器纵向(x轴方向)运动阻力系数,Cz(α)为潜器垂向(z轴方向)运动阻力系数,两个方向的阻力试验结果见文献[7]。
3 000 米和5 000米级海试的数据显示纵倾角θ接近零度,而由上式(3)可知,当纵倾角θ接近零度时攻角α可表示为θ的函数,采用数值算法可近似求出该函数,与文献[7]类似,阻力项写为:

0
2.2 浮力项B
随着潜器所处深度不同,海水密度和压力都会不同。一方面密度的变化会使潜器浮力发生相应变化;另一方面潜器的各耐压部件、密封部位和压力补偿部件的排水体积也会随着海水压力变化而变化。所以为了较准确地计算潜水器在各个深度的浮力,需要采用对应深度处的密度代入计算,而且需要较准确地计算潜器排水体积的变化量,潜器的浮力项可写为:
B=ρg (V-ΔV)
(5)其中:ρ=ρ (depth)为深度depth处的海水密度;ΔV为深度depth处潜器排水体积减少量,ΔV的变化分为两个大的阶段,第一阶段是潜器压载水箱注水或者排水阶段,此阶段ΔV变化速度较快;第二阶段是潜器压载水箱注满水后的阶段,此阶段潜器的排水体积变化主要是由于海水压力导致的,本文主要分析第二阶段的ΔV;所以V为潜器的压载水箱注满水后的排水体积。
根据水池均衡实验结果[7],潜器在水池平衡时总重20 807kg,而此时除了潜器本身的排水体积外,还有27kg铅块(密度11 700kg/m3)。此时潜水器在水池中平衡,有:

其中:Vm=潜器本体的排水体积。由(6)式可求得:

除了潜器本体,潜器携带的固定压载、可抛压载和作业工具等也产生一定的排水体积,这部分排水体积称为可变排水体积Vc。则潜器刚潜入水面以下时的排水体积(未考虑体积变化量)为:

对于排水体积变化量ΔV,如前所述,在海水压力下潜器排水体积发生变化的主要是耐压结构、密封部位和压力补偿部件,下面分两部分进行分析。
2.2.1 耐压结构排水体积变化
“蛟龙”号载人潜器上的主要耐压结构按外形可以分为两类:
(1)球壳:载人舱、可调压载水舱、高压气罐;
(2)圆柱壳:计算机罐、水声通信机罐、测深侧扫声纳罐、配电罐。
根据设计规范,可知潜器的耐压结构主体的材料在工作压力下还属于弹性范围内,所以可以采用理论公式计算排水体积变化量。
2.2.1.1 球壳耐压结构
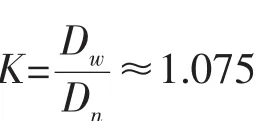

表1 “蛟龙”号主要球壳耐压结构Tab.1 Large spherical pressure hull of “JiaoLong”
球壳在下潜开始时内压已经存在,此时球壳的排水体积为:

其中Δr0为球壳径向变形量:

(10)式中:P1=球罐的内压,Ri=球壳内半径,t=壳厚,E=材料杨氏模量,μ=材料泊松比,各参数值可见表1。
当潜器下潜到某深度时,设海水压力为P2,此时潜器上的各个球壳同时受外压P2和内压P1,球壳的排水体积为:

其中Δr1为球壳径向变形量:

则各个球壳的排水体积减小量为:

2.2.1.2 圆柱壳耐压结构
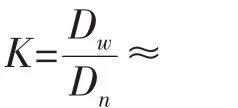

表2 “蛟龙”号主要圆柱壳耐压结构Tab.2 Large cylindrical pressure hull of “JiaoLong”
圆柱壳在下潜开始时内压已经存在,此时球壳的排水体积为:

其中Δr0和Δl0分别是圆柱壳的径向和轴向变形量:

(15)式和(16)式中:r2=圆柱壳外半径;r1=球壳内半径;l为圆柱壳轴线长度;其他参数的定义同(10)式。各参数的取值见表2。
当潜器下潜到某深度时,设海水压力为P2,此时潜器上的各个圆柱壳同时受外压P2和内压P1,圆柱壳的排水体积为:

其中Δr1和Δl1分别是圆柱壳的径向和轴向变形量:

则各个圆柱壳的排水体积减小量为:

则整个潜水器的耐压结构排水体积减小量为:

需要注意的是,圆柱筒形耐压结构的封盖可能是平封头,也可能是半球封头,且封头上一般有穿舱件和密封结构,所以封盖的变形量不能用理论公式方便地求出,这部分的变形量将并入下一类。
2.2.2 其他排水体积变化
除了主要的耐压结构,潜器上存在大量的密封部件和压力补偿部件,例如载人舱观察窗有机玻璃和观察窗基座之间存在摩擦,需要通过有限元接触分析才能计算观察窗有机玻璃的变形量。又例如潜器的耐压结构上的封头和耐压结构主体的装备处往往采用O型圈等密封措施。在这些密封部件处,装配体之间往往存在间隙,当海水压力小于某个值时,装配部位通过密封圈接触而装备体互相之间不接触,由于密封圈材料比较软(通常密封圈材料为橡胶),此时变形量随海水压力增加而有较大的增加;当海水压力大于某个值时,密封圈变形量已经足够大,使得装配体之间开始互相直接接触,此后变形量随海水压力增加的速度明显减小。这样的现象在压力筒试验中已经观察到了数次。例如模型球压力筒试验中密封端盖的变形量在约25MPa处存在明显的拐点。此外潜器上存在的许多压力补偿的部件和设备,例如充油电池箱、充油管路和电缆线等,这些设备和部件的内部承压部件往往外形复杂且包含多种材料。例如充油电池箱中承压的是一块块的电池,而这些电池的外形比较复杂,电池的等效杨氏模量也未知,所以采用结构分析来计算变形量变得不切实际。本文将所有不能通过球壳和圆柱壳理论公式计算变形量的部件的体积变化归为“其他排水体积变化”,且假设这一变化量为潜器所受的海水压力的函数,即:
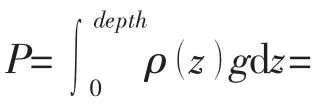
则潜器总的体积变化量为:

2.3 重力项W
根据水池均衡试验和海试的经验,潜器的重量可分为潜器本体重量和可变重量两部分组成。
根据水池均衡试验,潜器在水池中均衡时重量为20 807kg[7],此时除了潜器本体重量外,还包含有潜航员重量240kg、舱内耗材(包括二氧化碳吸收剂)13kg和可调压载水舱中140kg的淡水,则潜器本体重量为:

需要注意的是正常情况下潜器上安装的钛制采样篮是不会变动的,采样篮将算作潜器本体的一部分,故M0中包括了20kg的钛合金制采样篮,而D44潜次中改为重量约25kg的钢制采样篮,所以将D44潜次中钢制采样篮比原装钛制采样篮多出的5kg归入作业工具。因此,在计算作业工具的排水体积时,需要扣除更换采样篮带来的排水体积变化。潜器的重量可以划分为如表3所示的几个部分。将除了M0外的潜器可变重量之和记为MC,则潜器下潜时的重量M为:


表3 重量组成Tab.3 Weight components
2.4 潜器无动力潜浮运动平衡方程
潜器无动力潜浮运动遵守牛顿第二定律,运动方程如(1)式所示,在文献[7]中,潜器的下潜和上浮运动划分为以下几个阶段:
(1)压载水箱注水阶段;
(2)平稳下潜阶段;
(3)抛掉P1后减速阶段;
(4)潜器靠底阶段;
(5)抛掉P2后加速阶段;
(6)平稳上浮阶段;
(7)压载水箱排水阶段。
在文献[9]中,对本文模型的7个阶段均进行了详细的分析,出于篇幅考虑,此处只给出平稳下潜阶段和平稳上浮阶段的分析结果。
2.4.1 平稳下潜阶段
压载水箱注水完成后潜器排水体积不再有大的变化 (除了由于海水压力导致的排水体积减小),此阶段潜器的运动也是动态平衡的,即随着重力与浮力阻力之差程减速—加速—减速—加速……的过程,但是通过分析3 000米海试和5 000米海试的数据可见每个减速—加速循环的周期不长,且潜器的速度随着下潜深度的增加会逐渐降低,D44潜次从潜航员关闭压载水箱上阀门到抛载P1的下潜过程的速度—深度曲线如图2所示。

图2 D44平稳下潜阶段速度—深度曲线Fig.2 The velocity curve of the steady descent stage of dive 44
为了简化分析,本文将这一阶段潜器的运动近似为平稳运动,即认为加速度项为0,加速度为零则不考虑附加质量,此阶段潜器的各项力为:

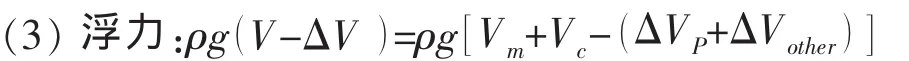

2.4.2 潜器平稳上浮阶段
潜器的重力、浮力和阻力达到动态平衡后,潜器的上浮运动可看成平稳运动,此阶段前期的运动称为平稳上浮阶段,此阶段潜器的各项受力为:

则潜器这一阶段的运动可以近似描述为平衡方程:
则潜器这一阶段的运动可以近似描述为平衡方程:
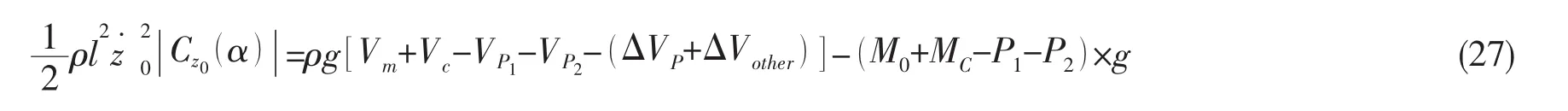
3 D44潜次数据分析
D44潜次实现了完全的无动力下潜上浮运动,其速度曲线相对没有实现无动力上浮下潜运动的潜次来说规律性比较明显,为了确定已经建立的无动力运动模型中的未知参数,本文对D44潜次的配载情况、航行记录和潜浮运动数据进行了详细的分析。
3.1 D44配载情况
D44潜次实现了无动力上浮下潜运动,其配载较合理,根据水池均衡试验结果和D44潜次的记录,D44潜次潜器的配载情况如下表4所示。

表4 D44配载情况Tab.4 Weight of dive 44
3.2 D44无动力潜浮运动数据
与无动力潜浮运动相关的D44潜次的海水密度—深度曲线、深度—时间曲线、速度—深度曲线如下图3-5所示。
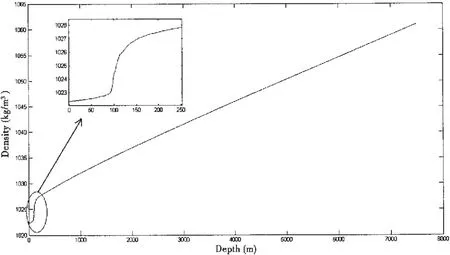
图3 海水密度—深度曲线Fig.3 Density curve
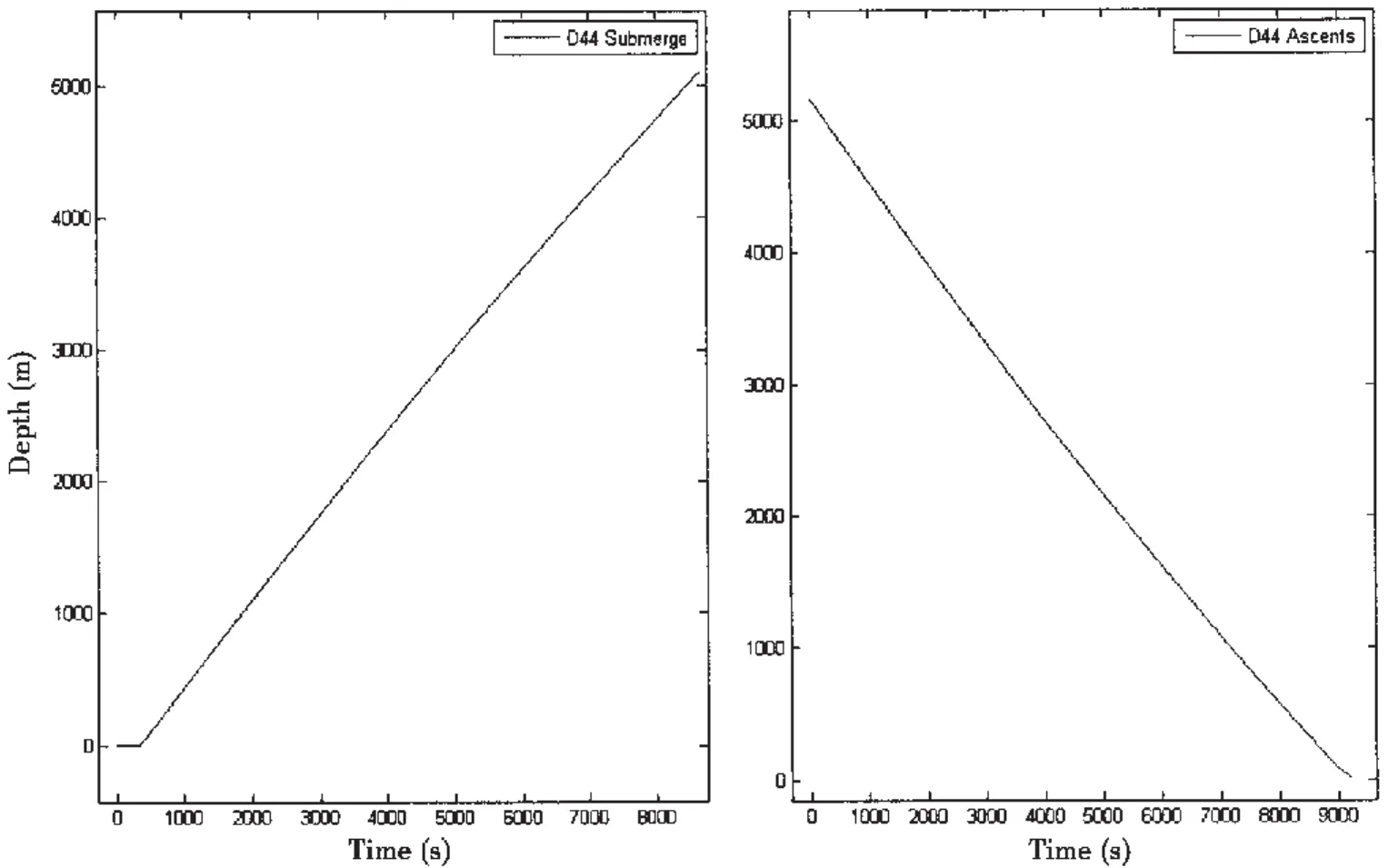
图4 D44下潜和上浮的深度—时间曲线Fig.4 The depth curve of submerge and ascent stage of dive 44
需要说明以下几点:(a)从图3中可看到深度大于1 000米后,海水密度随深度的变化呈线性,所以本文经将D44潜次的海水密度曲线外推至7 500米,且将该曲线和3 000米海试的海水密度曲线比较后发现,1000米以深的海水密度曲线差别较小。(b)图4和图5中的下潜曲线包括了从压载水舱开始注水到抛掉P1的整个下潜过程;而上浮曲线包括了抛掉P2到压载水舱开始排水的整个上浮过程。(c)与上浮至3 600米左右控制潜器上浮的操作记录相对应,可看到图5中平稳上浮阶段的速度曲线在3 600米附近有一个“尖刺”。
而本文主要分析潜器下潜和上浮的平稳运动阶段,故将加速度值较大的曲线段去除,仅对平稳阶段的曲线进行分析,由于潜器是动态平衡的,所以速度曲线存在较多小幅的加速—减速振荡,本文对D44平稳下潜阶段和平稳上浮阶段的速度曲线进行了光顺处理,以抓住平稳运动的规律,D44平稳下潜阶段的速度曲线和光顺后的曲线见图6所示,同理D44平稳上浮阶段的速度曲线和光顺后的曲线见图7所示。

图5 D44下潜和上浮的速度—深度曲线Fig.5 Velocity curve of submerge and ascent stage of dive dive 44
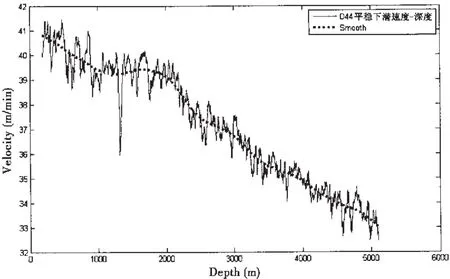
图6 D44平稳下潜阶段速度—深度曲线及光顺后曲线Fig.6 The smoothed velocity curve of the steady descent stage of dive 44

图7 D44平稳上浮阶段速度—深度曲线及光顺后曲线Fig.7 The smoothed velocity curve of the steady asscent stage of dive 44
4 模型参数辨识
4.1 平稳下潜阶段
由平稳下潜阶段的平衡方程式(26)可知,无动力运动模型中的“其他排水体积变化量—ΔVother”是未知的,需要由5 000米海试D44潜次的平稳下潜阶段的曲线求得。D44下潜的ΔVother对海水压力P的曲线见图8所示,由光顺后曲线可看到在约20-26MPa之间潜器的排水体积变化量存在明显的拐点,可认为潜器上大部分设备的密封部位和补偿部位在20-26MPa时达到紧实,此后ΔVother随P增长的速度降低(表现为图上的曲线斜率降低)。
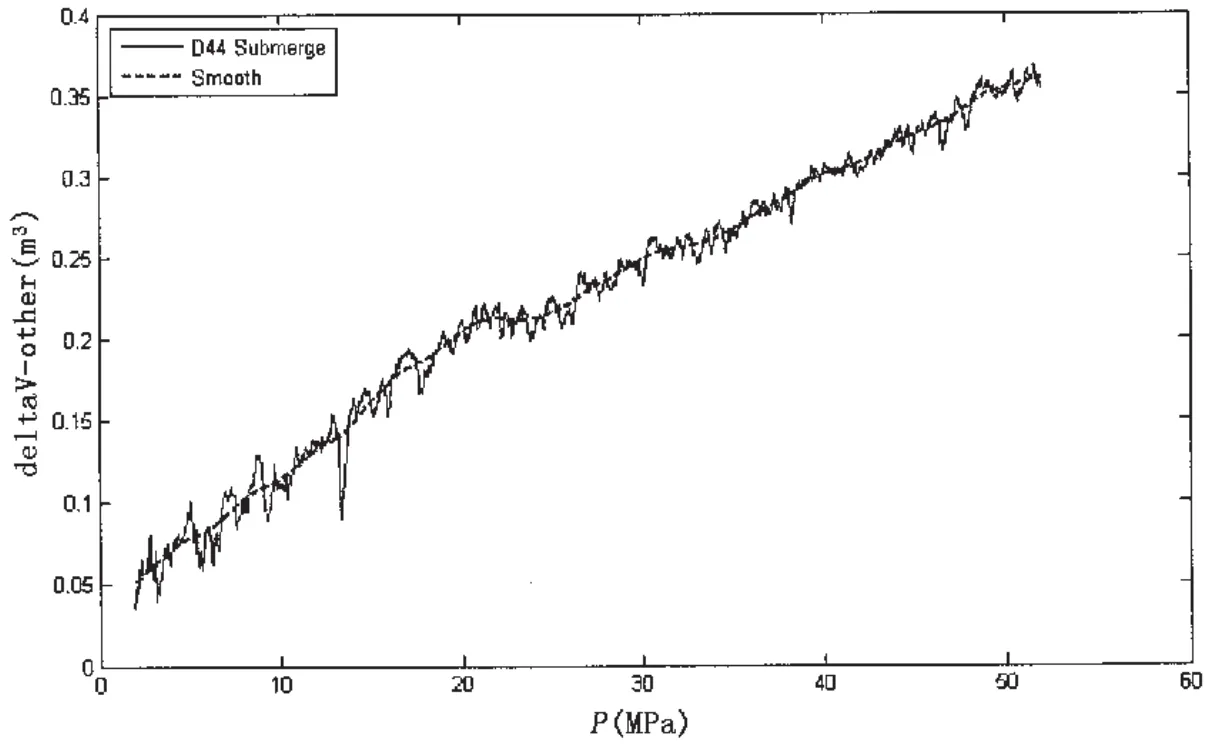
图8 D44平稳下潜阶段ΔVother随海水压力P变化曲线Fig.8 The ΔVothercurve of the steady descent stage of dive 44
4.2 平稳上浮阶段
平稳上浮阶段的平衡方程见(27)式,ΔVother同样是未知的,需要由5 000米海试D44潜次的平稳上浮阶段的曲线求得,需要注意的是由于压缩量恢复有一定的滞后,上浮阶段的ΔVother和下潜阶段的ΔVother可能不同。ΔVother随P变化的曲线见图9,可见当海水压力大于6MPa时潜器ΔVother随P的变化可近似为直线,而P在4.5MPa至6MPa之间曲线存在明显的拐点,当P小于4.5MPa时ΔVother减小的速度明显加快,可认为在4.5~6MPa之间潜器密封部件的密封面脱离闭合状态,当然,仅由D44潜次一个潜次的数据还不能下充分的结论。
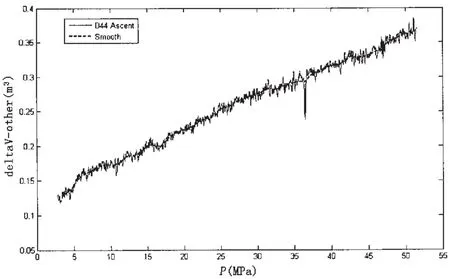
图9 D44平稳上浮阶段ΔVother随海水压力P变化曲线Fig.9 The ΔVothercurve of the steady ascent stage of dive 44
4.3 参数取值
将图8和图9中的D44下潜和上浮求出的ΔVother随海水压力P变化的光顺后的曲线取出放在同一张图中比较,如图10所示。可见:随着下潜深度增大,下潜和上浮的ΔVother值逐渐接近,这个现象和实际情况较符合,因为D44潜次最大潜深为5180米,在较深的深度处,例如5 000米处,潜器下潜和上浮至该深度处的压缩量应该差别不大,因为潜器下潜超过5 000米深度只有180米,在最深的5 180米处作业接近2小时,这2个小时内潜器相当于处在保压状态,ΔVother将随着作业时间增加而略有增加,但是从5 180米上浮至5 000米时的压缩量和下潜至5 000米时的压缩量不应有大的差别。

图10 D44航次下潜和上浮ΔVother随P变化曲线(光顺后)比较Fig.10 Comparison of smoothed ΔVothercurve of the steady descent stage and ascent stage of dive 44
为了将5 000米海试的结果外推至7 000米,需要对图10中的曲线进行分析和外插。由图10,下潜的ΔVother-P曲线可近似为三段:
(1)P<13MPa时,此阶段潜器的ΔVother随P的变化可近似为直线;
(2)13MPa<P<33MPa时,此阶段潜器的ΔVother随P的变化出现拐点,直接取由D44下潜数据反求出的光顺后的曲线段;
(3)P>33MPa时,ΔVother随P的变化也可近似为直线,将该直线段外插至76.7MPa(约7 500米),以便于估算7 000米处的ΔVother。
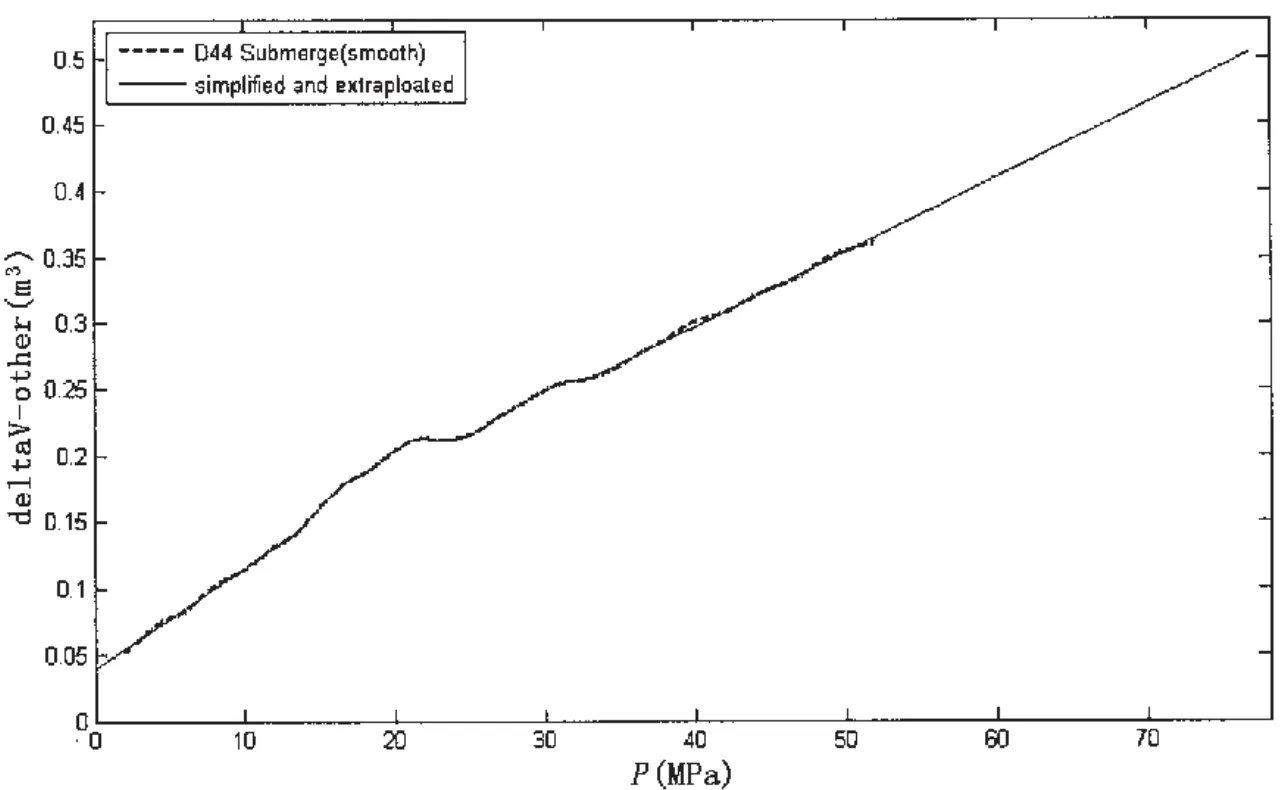
图11 下潜ΔVother-P曲线的处理和外插Fig.11 Extrapolation of ΔVothercurve of the steady descent stage of dive 44
近似结果如上图11所示。
类似的,上浮曲线也可分为三段:
(1)P<3MPa时,此阶段潜器的ΔVother随P的变化可近似为直线;
(2)3MPa<P<7.6MPa时,此阶段潜器的ΔVother随P的变化出现拐点,直接取由D44上浮数据反求出的光顺后的曲线段;
(3)P>7.6MPa时,ΔVother随P的变化也可近似为直线,将该直线段外插至76.7MPa(约7 500米)。
上浮近似结果如下图12所示。
将处理并外插后的下潜和上浮ΔVother-P曲线置于同一张图中,如图13所示,可看到下潜和上浮曲线的交点在约5 736米处,与最大下潜深度5 180米差556米,一方面可能是由于潜器在高压下作业的过程中ΔVother会存在少量增加,另一方面也可能是由于上浮和下潜的数据存在误差等导致。

图12 上浮ΔVother-P曲线的处理和外插Fig.12 Extrapolation of ΔVothercurve of the steady ascent stage of dive 44

图13 上浮和下潜的ΔVother-P曲线Fig.13 Used ΔVothercurve
可见,在前述模型的基础上,为了更准确地描述潜器上浮阶段的运动,需要增加新的变量:作业阶段(保压阶段)体积压缩量ΔVwork—反应潜器在底部作业过程中,即保压状态下排水体积减小量。对指定的潜器,ΔVwork是作业压力和作业时间的函数,由于“蛟龙”号的作业时间基本固定,且还没有足够的数据支持,本文在此暂时假设ΔVwork只是作业压力的线性函数:

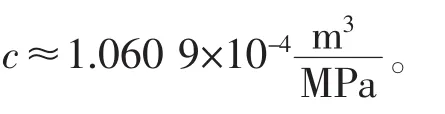
则平稳上浮阶段平衡方程改为:
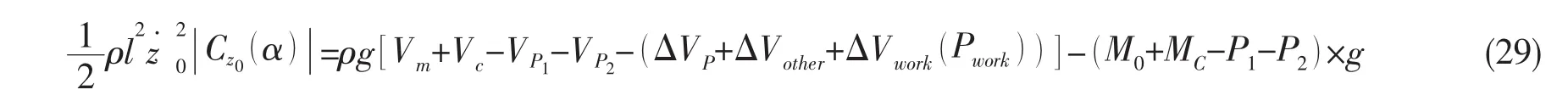
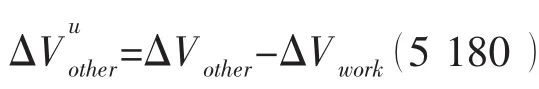
4.4 程序修改
根据以上计算模型和参数取值,对原有程序进行了修改,界面也进行了改进,如图14所示。计算输入分为两个部分,第一部分是预计作业深度Z0、上浮抛载、下潜抛载及密度曲线选择;第二部分是潜器重量和排水情况。计算结果将输出Z0处的均衡情况、下潜速度曲线和上浮速度曲线,同时也给出下潜/上浮的速度均值以及时间估算。
程序的大部分操作和原程序类似,但是存在以下不同:
(1)程序要求较准确地输入潜器各部分重量以及排水体积情况。注意“舱内耗材”、“舱内人员”和“压载水箱注水”三项的排水体积为0;浮抛载和下潜抛载需要根据计算均衡结果人工进行调整;

图14 程序界面图14 GUI of the program
(2)程序的“参考密度曲线”为5 000米海试得到的密度—深度曲线拓展至10 000米的密度曲线;“实测密度曲线”为下潜海区的实测密度—深度曲线,数据格式见程序目录下的 “深度密度曲线.csv”文件,且要求“深度密度曲线.csv”中的第一个深度是0,最后一个深度大于程序输入的Z0(大深度下密度-深度曲线可近似为直线,所以操作者可将实测密度-深度曲线的后半段 (例如对于Z0=7 000米,而实测曲线只有6 000米的数据,则操作者可以对3 000米以深的密度—深度曲线进行线性拟合,操作者可以根据具体曲线形状在excel中方便地进行线性拟合和外插操作,本程序不再提供该功能)线性外插拓展至需要的深度 (一般可外插至10 000米),并将拓展后的曲线保存至 “深度密度曲线.csv”中)。
(3)程序的输出调整为下潜深度Z0处的均衡情况。如果要求Z0处潜器达到均衡,则应调整下潜抛载P2(因为潜器下潜至Z0处时P1已经被抛掉,所以P1不影响均衡位置)使结果接近于0;如果要求Z0处潜器具有足够的坐底力,则应调整下潜抛载P2使结果接近于设计坐底力(“蛟龙 ” 号 设 计 坐 底 力 ≈40)。
4.5 D44潜次计算结果
采用修改后的程序,将D44潜次的载荷数据填入后采用程序进行计算,计算结果如图15所示。
可见5 180处潜器重力浮力差(即坐底力)为35kg,与40kg比较接近,且速度曲线和图6及图7类似。
5 结 语
本文根据“蛟龙”号5 000米海试的D44潜次无动力潜浮海试数据对“蛟龙”号无动力潜浮运动模型进行了再分析,改进了3 000米海试后提出的分析模型,主要是采用了可变的体积压缩率的概念,且对程序进行了修改,开发出了更为可靠的蛟龙号载人潜器无动力潜浮运动分析系统,使得计算结果更接近实际情况,程序界面更加符合实际应用,为2012年的7 000米级海试做好了准备,也为4 500米载人潜器无动力潜浮运动的设计打下了基础。
[1]Busby,Frank.Manned Submersibles[M].Arlington,VA:Office of the Oceanographer of the Navy,1976.
[2]Allmendinger,Eugene E.Submersible Vehicle Systems Design[M].ill.Jersey City,NJ:Society of Naval Architects and Marine Engineers,1990.
[3]朱继懋主编.潜水器设计[M].上海:上海交通大学出版社,1992.
[4]崔维成,马 岭.潜水器设计中所要解决的水动力学问题[C].第九届全国水动力学学术会议暨第二十二届全国水动力学研讨会文集,吴有生,刘 桦,许唯临,周连第,杨显成主编,海洋出版社,北京,2009:9-29.
[5]刘正元.7000米载人潜器无动力潜浮运动研究[R].无锡:中国船舶科学研究中心科技报告,2004.
[6]刘正元.潜水器大攻角范围内运动的仿真[J].船舶力学,2005,9(2):54-59.Liu Zhengyuan.Simulation of submersible motion in large attack angle[J].Journal of Ship Mechanics,2005,9(2):54-59.
[7]刘正元,潘彬彬,崔维成.7000m载人潜器海试试验数据整理和分析[R].无锡:中国船舶科学研究中心科技报告,2010.
[8]范欣珊.压力容器的应力分析与强度设计[M].北京:原子能出版社,1979.
[9]潘彬彬,崔维成,叶 聪,刘正元.7000m载人潜器无动力潜浮运动分析[R].无锡:中国船舶科学研究中心科技报告,2011.

