潜器在冲击载荷下的运动和控制研究

程嘉欢，连 琏，刘可峰

(上海交通大学海洋工程国家重点实验室，上海 200240)

低速潜器往往会受到冲击载荷的作用，从而产生比较复杂的运动响应，影响任务执行和航行安全。因此，对其进行研究在潜器运动和操纵性领域有比较重要的意义。

拟研究潜器在水下受到冲击载荷时的运动响应与控制。潜器水下发射火箭是一个两相流动和箭体运动耦合的复杂问题。火箭出筒过程中，燃气射流会对发射筒底产生显著冲击。火箭出筒后，发射筒内的高温高压混气溢出，由于惯性使筒内压强低于筒外静水压强，导致海水倒灌形成“水锤”冲击筒底。之后在发射筒内形成一系列压缩波与膨胀波在筒底与筒口之间来回振荡，造成潜器受到周期性脉动压力，即水锤效应。水锤效应会在火箭出筒后的一段时间内仍对潜器的姿态产生持续影响。

这一课题国内研究与公开资料较少。在水下发射火箭领域，鲁传敬等［1］提出了火箭水下发射时箭体与水、燃气的耦合计算方法。李杰等［2］用Rayleih-Plesset方程对火箭尾部燃气泡进行建模和模拟。傅德彬等［3-4］利用动网格和VOF模型求解燃气、水和水蒸气之间的耦合，计算了燃气和海水倒灌对筒底的冲击压强。倪火才［5］通过实验数据定性地分析了水锤效应的机理和规律。徐新琦等［6］用四元数方法建立了火箭的水下运动轨迹模型。在潜器的运动响应与控制方面，陈建军［7］根据水锤压力实验数据简单分析了潜器在水锤效应下的升沉运动。李文龙等［8］用Gertier六自由度方程，对潜器受到发射冲量后的运动控制进行了仿真。由文立等［9］利用DDAM方法计算了潜器在冲击载荷中的响应。刘正元等［10］对低速大攻角运动的潜水器建立了非解析式数学模型。这些研究着重把载荷描述为冲量，忽略了水锤效应的后续影响。至今还尚未发现有论文系统分析计算完整发射冲击载荷下潜器的运动规律与控制。

通过建立模型潜器在水下的六自由度非线性运动方程，对潜器基本运动进行仿真，并通过仿真结果和实验数据的比较，验证了数学模型的准确性和有效性。根据这一模型，系统计算潜器在水下发射火箭时在完整冲击载荷下的运动响应和控制，并分析机理和规律。

1 数学模型的建立

1.1 潜器六自由度非线性运动模型

采用ITTC推荐和SNAME术语公报的坐标体系［11］，在格特勒潜器标准运动方程［12］的基础上，建立潜器六自由度非线性运动方程组，具体如下。

轴向力方程:

侧向力方程:

垂向力方程:

横摇力矩方程:

纵倾力矩方程:

偏航力矩方程:

以上各式中:m为潜器的质量，W=mg为潜器在空气中的重量，B为所受浮力;(xG，yG，zG)为质心坐标，(xB，yB，zB)为浮心坐标;u，v，w 为纵向、横向、垂向速度，p，q，r为横摇、纵倾、回转角速度;φ，θ，ψ 为横摇角、纵倾角和首向角，δr，δb，δs分别为方向舵、首水平舵和尾水平舵的舵角，Ixx，Iyy，Izz为潜器在动坐标中的惯性矩;T为螺旋桨推力，ΔWadjust为潜器浮力调整水舱的注排水量，xadjust为潜器浮力调整水舱的纵向坐标，ΔW为发射火箭时产生的静载差，MΔW为静载差引起的纵倾力矩，P为潜器所受发射载荷力，MP为潜器受到的发射载荷力矩;其余为潜器的水动力系数，为潜器自身固有属性。

螺旋桨推力T由螺旋桨的水动力性能和转速计算得到，对应下文2.2中的推力模块，有:

式中:ρ为水的密度，D为螺旋桨直径，Ct为螺旋桨推力系数，n为转速。方向舵与首、尾水平舵舵角δr，δb，δs由下文2.2中的方向舵与水平舵两个模块计算得出，它们满足:

式中:δrd，δbd，δsd为期望舵角，R1，R2，B1，B2，S1，S2为操舵系统固有属性。由于火箭自重往往与发射筒进水后的重量不同，因此产生静载差ΔW。

式中:k为发射火箭总数，Pwi为发射第i枚火箭后的进水量，Pmi为第i枚火箭自重。潜器通过浮力调整水舱的注排水来平衡静载差，注排水量ΔWadjust满足时间t的线性关系:

式中:vadjust为注排水速度，TP为火箭发射的时间点。

1.2 潜器的受力分析

在发射火箭的过程中，潜器的受力主要包括静力、艇体水动力和发射载荷。前两者在文献［13］中有详细描述;这里描述发射载荷，包括发射反冲力，燃气负压区和水锤压力。

1.2.1 发射反冲力

火箭点火之后，高温高压燃气由喷口进入发射筒，产生发射反冲力。发射反冲力作用于发射筒底，时间短，一般仅为数百毫秒;压强大，达到4～8 MPa;随着火箭出筒迅速衰减。

式中:XT1，YT1，ZT1和 KT1，MT1，NT1分别是反射冲击力和力矩在 x，y，z轴上的分量;冲击力 cj(r，t)是离发射筒中心的距离r和时间t的函数;A1是冲击力在发射筒底的作用范围;xT1，yT1分别是ZT1在x和y方向上的作用力臂。

1.2.2 高压燃气造成的负压区

火箭出筒以后，由于惯性，筒内的高温高压混气(燃气和水蒸气)迅速向外扩散，使得发射筒口附近出现一个低于周围静压的负压区。该负压区随着远离筒口而逐渐衰减。

式中:XT2，YT2，ZT2和 KT2，MT2，NT2分别是负压区压力和力矩在 x，y，z轴上的分量;负压区压力 fy(r，t)是离发射筒中心的距离r和时间t的函数;A2是冲击力在发射筒底的作用范围;xT2，yT2分别是ZT2在x和y方向上的作用力臂。

1.2.3 水锤压力

在发射筒口形成负压区之后，在重力和发射筒内外压力差的共同作用下，海水倒灌入发射筒，并形成“水锤”冲向筒底，形成水锤压力。之后形成压缩波与膨胀波在筒底与筒口来回振荡，使潜器受到脉动压力，如图1所示［5］。水锤压力曲线是脉动的。海水倒灌入发射筒后的第一个压力峰值最大，甚至超过了火箭发射时燃气射流对发射筒的冲击压力。随后压力峰值明显衰减，第二个峰值压力相当于第一个峰值压力的一半，之后压力峰值的衰减减慢，并最终趋向于当地的平衡压力。每个压力峰值之间的时间间隔大体相等，称之为压力脉动周期。

2 实验模型与仿真模型

采用模型实验的方式验证数学模型的有效性。导入实验模型的水动力参数，建立实验潜器的运动仿真模型。通过对潜器基本运动的仿真结果和实验数据进行比较，验证仿真模型的有效性。在此基础上进一步研究发射火箭时潜器的运动响应与控制。

2.1 实验模型介绍

采用的实验验证模型利用Thunder Tiger公司的潜器模型改装而成，参见图2。

图1 水锤压力实验曲线Fig.1 Test data of water hammer pressure

图2 实验模型示意Fig.2 Perspective view of the test model

该模型采用电机推进，单桨，安装有艏舵和十字形艉舵，分别各有一台伺服电机控制尾方向舵和首尾水平舵，安装电罗盘和深度计用于测量航向和深度。模型的主要数据参见表1。

表1 实验模型的主要参数Tab.1 Principal parameters of test model

该模型潜器的推进器是直流电机，螺旋桨转速n由电机的Md和螺旋桨扭矩Q决定的:

方向舵和水平舵均视为一阶线性时不变系统，且首尾水平舵同步操作，R1=11.53，R2=10.377，B1=S1=7.69，B2=S2=6.921，根据式(8)，其传递函数计算如下:

2.2 仿真模型的建立与验证

水动力系数是仿真模型中的关键参数。根据文献［12］第六章的近似计算方法和文献［14］的数据，测绘并导入实验模型的相关参数，估算其水动力系数，主要结果参见表2。

表2 实验模型的主要水动力系数Tab.2 Key hydrodynamic coefficient of the test model

利用Simulink软件，建立了潜器的运动仿真模型，如图3所示。仿真模型中，推进模块输出推力T，水平舵和方向舵模块分别输出控制舵角δb，δs，δr。首尾水平舵同步操作，由于实验模型上舵的转动速度较快，因此其初始操作简化为阶跃操舵形式，饱和舵角为30°。推进系统、方向舵和首尾水平舵均采用PID控制方式。因此控制舵角的响应方程满足:

式中:δb，δs，δr是输出的控制舵角;ψd，θd是目标姿态角;ψ，θ是目前的姿态角;KD1，KP1，KI1，KD2，KP3，KI2为PID控制器的参数。

图3 潜器仿真模型Fig.3 Perspective view of the simulation model of the vehicle

为了验证仿真模型的有效性，对六自由度基本运动进行了运动仿真和模型实验。经过大量实验确定该实验模型控制系统的最佳PID参数，参见表3。在同样的PID参数下，用仿真模型对相应运动进行模拟，并将两组结果进行对比。

表3 PID控制器参数Tab.3 Parameters of the PID controller

第一组为水平面运动:定向航行实验。取目标航向为160°，航速3 kn，仿真结果和实验数据如图4所示。由图可见，从40 s开始，两者结果中潜器首向角均在目标航向160°附近作小幅振荡。仿真结果与实验数据匹配较好，该仿真模型的水平面运动与真实情况较为接近。

图4 潜器定向航行下的时间—首向角曲线Fig.4 Time-heading angle curve of the submarine under constant-bearing course

第二组为垂直面运动:定深航行实验。取航速为3 kn，目标深度为1 m，仿真结果和实验数据如图5所示。如图，两者均在60 s左右初次达到目标深度，超调量在0.1 m左右，仿真结果收敛速度较快，但两者的匹配仍然较好。因此仿真模型在垂直面上的运动也较有效。

图5 潜器定深航行下的时间—深度曲线Fig.5 Time-depth curve of the submarine under fixed-depth-way

3 潜器在冲击载荷下的运动响应与控制研究

假设模型潜器在水下热发射一枚火箭，发动机喷口总压8 MPa，燃气温度3 200 K，点火时发射筒内充满与外界静水压平衡的空气，火箭在TP=200 s时从直径0.55 cm的发射筒中点火发射，发射筒形心位于中纵剖面上，在动坐标系原点艇艏方向0.1 m处。发射静载差ΔW=0.4 kg。参照文献［4-5］中的受力规律，发射单枚火箭时的载荷曲线如图6所示。第一个压力峰值表示点火时燃气射流对潜器的冲击压力，第二压力峰值为水锤效应产生的第一个水锤压力峰值，其大小与发射时燃气冲击压力值近似，随后的波动是水锤压力在发射筒内形成的压缩波与膨胀波来回传播振荡引起的周期性脉动压力。

3.1 潜器的运动响应

潜器在受到如图6的冲击载荷之后，将产生运动响应，包括速度损失、深度变化和纵倾角变化。分别设定潜器的初始速度为2 kn到4 kn，分别计算其运动响应和姿态变化。

图7所示为潜器的速度损失情况。在火箭点火发射之后，潜器的速度会有损失，但在水锤效应第一个压力峰值之后开始恢复。潜器原有的航速越大，速度损失越小，恢复速度越快。

图8所示为潜器的深度变化情况。火箭点火时潜器受到巨大的发射反冲力，产生较大的升沉速度，下潜深度迅速增加;之后由于艇体上方负压区的产生和随之而来的海水倒灌，深度变化曲线产生较大振荡;随着水锤压力峰值的衰减，深度曲线振荡幅度减小，最后潜器在一个新的深度稳定下来。由图可知，潜器原有的航速越高，深度变化越小，稳定深度需要的时间越少，对深度保持越有利。

图9所示为潜器纵倾角变化曲线。在火箭点火时，巨大的燃气射流冲击使得潜器迅速产生较大的首倾角，水锤压力的第一、第二个压力峰值更进一步加剧了这一现象。迅速产生的首倾角使潜器受到较大的反向水动力矩的作用，其回复作用在载荷较大时并不明显。在水锤压力第二个峰值之后，载荷迅速衰减，潜器的首倾角便在水动力的作用下迅速变小，并由于惯性产生尾倾。随后，在艇体水动力和残存的水锤压力的共同作用下，纵倾角的振荡幅度逐渐衰退。潜器的初始航速越高，首尾倾的幅度越小，艇体姿态保持越好。

图6 发射火箭时潜器受到的冲击载荷曲线Fig.6 Impact load curve of the vehicle during the process of rocket launching

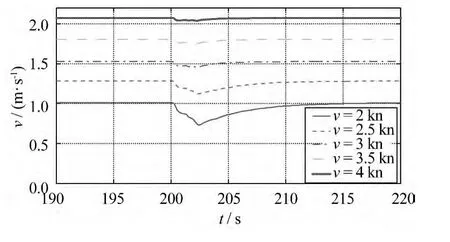
图7 潜器在水锤效应下的速度变化曲线Fig.7 Velocity curve of the vehicle under water hammer pressure

综上所述，潜器的航速越高，发射载荷对潜器运动的影响越小，这符合现有对潜器水下发射火箭的认识和规律总结［12］。但是，潜器航速越高，对火箭水下运动轨迹和出水姿态的影响越大，所以潜器在发射火箭时的航速选择是一个需要平衡的问题。

图8 潜器在水锤效应下的深度变化曲线Fig.8 Depth curve of the vehicle under water hammer pressure

图9 潜器在水锤效应下的纵倾角变化曲线Fig.9 Pitch curve of the vehicle under water hammer pressure

3.2 潜器的运动控制

潜器在受到如图6的载荷之后，使用舵和浮力调整水舱对运动和姿态进行控制，水舱注排水速度vadjust=2.96×10-2m3/s。设定潜器的速度为2 kn到4 kn，分别进行仿真分析。

图10 潜器在控制下的深度变化曲线Fig.10 Depth curve of the vehicle under control

图10所示为潜器深度变化曲线。由图可见，在受到发射冲击载荷的扰动之后，通过及时的操控，相比无控制时深度变化值明显减少，在50 s左右的时间基本恢复了原来的深度，控制方式比较有效。潜器的航速越低，控制效果越差，恢复深度需要的时间越长，反向上浮的深度越大。

图11所示为纵倾角变化曲线。由图可见，在进行控制以后，纵倾角的变化值缩小，能较快恢复水平状态。由于水下火箭发射对潜器纵倾角有很高的要求，因此有利于迅速进行下一轮发射。与深度控制类似，潜器原有的航速越低，控制效果越差，恢复水平所需时间越长。

图12为水平舵舵角的变化曲线。由图可见，为了达到较好的控制效果，需要舵角作频率较快的操作。这在模型潜器上比较容易实现，但是对于真实潜器，实现难度较高。因此，需要辅助动力帮助潜器更好的进行控制，比如槽道螺旋桨。

综上所述，可以通过操作水平舵和浮力调整水舱对潜器的运动进行较为满意的控制。在低速状态下，控制效果随着航速递增。

图11 潜器在控制下的纵倾角变化曲线Fig.11 Pitch curve of the vehicle under control

图12 潜器水平舵的变化曲线Fig.12 Diving plane curve of the vehicle

4 结语

通过建立模型潜器在水下的六自由度非线性运动模型，对潜器的六自由度基本运动进行仿真，通过仿真结果和水池实验数据的对比，验证了模型的准确性和有效性。根据这一数学模型，计算分析了潜器在完整火箭发射后效(发射冲击与完整的水锤效应)作用下的运动响应和运动控制。结果表明，发射载荷对潜器的运动有较长时间的显著影响，潜器的初始速度越大，影响程度越小，影响时间越短。通过操舵和压载水舱的调节，可以对潜器的运动进行较满意的控制，在一定范围内控制效果随着初始航速递增。对于真实的潜器，则建议需要加装辅助动力帮助潜器更好的进行控制。

［1］ 鲁传敬，陈 芳，樊 泓，等.导弹水下点火的流体动力研究［J］.航空学报，1992，13(4):B124-B130.(LU Chuan-jing，CHEN Fang，FAN Hong，et al.The fluid dynamic research on the under-water ignition of missile［J］.Acta Aeronauticaet Astronautica Sinica，1992，13(4):B124-B130.(in Chinese))

［2］ 李 杰，鲁传敬.潜射导弹尾部燃气后效建模及数值模拟［J］.弹道学报，2009，12(4):6-8.(LI Jie，LU Chuan-jing.The model of combustion gas bubble of submarine-launched missile and numerical simulation［J］.Journal of Ballastics，2009，12(4):6-8.(in Chinese))

［3］ 傅德彬，于殿君，张志勇.气密条件下水下热发射流场数值研究［J］.固体火箭技术，2011，34(2):135-160.(FU De-bin，YU Dian-jun，ZHANG Zhi-yong.Numerical simulation of complex flow field for missile launched under-water under gas proof conditions［J］.Journal of Solid Rocket Technology ，2011，34(2):135-160.(in Chinese))

［4］ 傅德彬，于殿君，张志勇.潜射导弹离筒后海水倒灌效应数值分析［J］.固体火箭技术，2012，35(2):157-160.(FU De-bin，YU Dian-jun，ZHANG Zhi-yong.Numerical simulation of hydrodynamic impact effect after submarine launched missile leaves the launcher［J］.Journal of Solid Rocket Technology，2012，35(2):157-160.(in Chinese))

［5］ 倪火才.潜载导弹水下垂直发射时的“水锤”压力研究［J］.舰船科学技术，2000(5):46-49.(NI Huo-cai.Research on water-hammer pressure of under-water missile launching［J］.Ship Science and Technology，2000(5):46-49.(in Chinese))

［6］ 徐新琦，田 兵，李兵尚.潜地导弹水下弹道建模与仿真［J］.弹箭与制导学报，2010，30(5):149-152.(XU Xin-qi，TIAN Bin，LI Bing-shang.The model and simulation of submarine to surface missile underwater trajectory［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2010，30(5):149-152.(in Chinese))

［7］ 陈建军.潜载导弹垂直发射对耐压壳体结构的冲击响应分析［D］.哈尔滨:哈尔滨工程大学，2008.(CHEN Jian-jun.The dynamic response of submarine structure acting by missile impact loads in vertical launch［D］.Harbin:Harbin Engineering University，2008.(in Chinese))

［8］ 李文龙，徐亦凡，李 博.水下连续发射导弹时潜艇与姿态控制仿真［C］//中国控制与决策学术年会.2004.(LI Wen-long，XU Yi-fan，LI Bo.Simulation of controlling the gesture and depth of ssbn while project in series［C］//Proceeding of 2004 Chinese Control and Decision Conference.2004.(in Chinese))

［9］ 由文立，周方毅，詹发民，等.舰艇导弹发射装置冲击仿真［J］.舰船科学技术，2010，32(9):107-110.(YOU Wen-li，ZHOU Fang-yi，ZHAN Fa-min，et al.Simulation of resistant shock capability of missile launcher［J］.Ship Science and Technology，2010，32(9):107-110.(in Chinese))

［10］刘正元，沈明学，刘 涛.深水潜器运动的非解析式数学模型［J］.中国造船，2010，51(2):92-98.(LIU Zheng-yuan，SHEN Ming-xue，LIU Tao.A non-analytic mathematical model of deep-sea submersible［J］.Shipbuilding of China，2010，51(2):92-98.(in Chinese))

［11］ Nomenclature for Treating the Motion of a Submerged Body Through a Fluid［R］.SNAME Technical and Research Bulletin 1-5，1952.

［12］施生达.潜艇操纵性［M］.北京:国防工业出版社，1995.(SHI Sheng-da.Submarine Maneuverability［M］.Beijing:National Defence Industry Press，1995.(in Chinese))

［13］刘 鹰，赵 琳.潜艇仿真数学模型的推导求解［J］.哈尔滨工程大学学报，1999，20(2):26-33.(LIU Ying，ZHAO Lin.The derivation of submarine simulation math model［J］.Journal of Harbin Engineering University，1999，20(2):26-33.(in Chinese))

［14］尚桂杨.移动式水下观测网验证平台［D］.上海:上海交通大学，2011.(SHANG Gui-yang.Development of a testbed of underwater moblie sensing network［D］.Shanghai:Shanghai Jiao Tong University，2011.(in Chinese))