舰船气泡尾流分布的BPBE表征方法研究

王桂军，闫雪飞，金良安，苑志江

(海军大连舰艇学院 航海系，辽宁 大连 116018)

水面舰船在航行过程中会在其尾部一定区域内留下一条长达数千米的具有特殊性质的尾流，其中的气泡尾流由于可以被尾流自导鱼雷探测到，具有重要的军事和民用价值，是国内外相关领域的一个研究热点［1］。气泡尾流可以按离舰船尾部的距离长短划分为近程尾流和远程尾流，其中关于远程静尾流中气泡动力学特性的研究屡见不鲜［1］，而专门针对近程湍流尾流的研究报道却很少见诸文献。

目前对舰船尾流的气泡特性研究还主要考虑气体的传质因素，而很少有系统考虑聚并影响的。Stewart采用大涡模拟技术(LES)和拉格朗日粒子跟踪方法(LPD)对尾流环境下的气泡动力学进行了研究，重点分析了气体传质与扩散对气泡群尺寸演变的影响［2］。陈圣涛采用气液两相流模型分别对近程和远程气泡尾流含气量的时间分布特征做了比较全面的数值模拟和实验研究，指出进程气泡尾流含气量以乘幂形式衰减，而远程尾流基本以指数形式衰减，然而陈的方法过于复杂，体现在占有大量运算内存和时间，一个算例需要在集成计算机上运算3 400个CPU小时［3］。朱东华［4］曾以MINER［5］的初始值生成方法为依据，对尾流的气泡数密度分布进行了三维数值模拟，基于波尔兹曼型气泡输运方程和雷诺平均方程计算出了尾流中不同尺寸的气泡数密度分布特征，结果表明气泡尾流主要位于10～200 um之间。刘慧开建立了海洋表层气泡运动和半径变化的数学模型，发现小于临界半径(74.1 um)的气泡会迅速溶解，而大于临界半径的气泡会上升到水面破裂，由此得出海水中的气泡主要以50～74 um之间居多［6］。Carrica采用气液两相流技术对舰船尾流中不同位置处的气含量及气泡数密度分布进行了数值模拟［7］，但没有对聚并这一重要因素进行必要的深入分析，而且Carrica的算法同样要占大量存储和运算时间(200CPU h)，普通电脑上根本无法实现，难以达到实时应用的要求。

综上可知，当前关于气泡尾流的特征研究还存在很多缺陷，对气泡聚并因素的认识不足。1946年，美国国防研究委员会第六局用声呐测量了以航速15 kn航行的驱逐舰产生的尾流气泡分布规律，发现尾流中气泡直径为0.08～1.07 mm的气泡数密度高达5.98×106/m3，如此高的数密度会不可避免导致聚并的发生［8］。此外，Smirnov在对对非动力船只的近程尾流的研究中，也着重分析了气泡聚并在近程尾流中发生的可能性，提出了气泡聚并的重要作用，但并未对此进行深入研究［9］。这里在对BPBE方程修正的基础上，首次将其运用于对气泡尾流数密度和气含量的研究上，重点探究了聚并因素的作用，且模型具有简单，可操作性强的特点，还可节省大量的计算时间(完整模型对3 000 m长度尾流的推演时间不超过4 s)。

1 模型的构建过程

1.1 模型构建的思想与基础

1.1.1 基本思想

传统对气泡尾流的数值模拟将尾流速度与气泡运动耦合在一起进行求解，大大的增加了模型求解的复杂性和难度，无法满足军事应用的实时性要求。鉴于此，采用BPBE方程进行相关求解，可将尾流速度的求解和气泡特性的计算分开而来，只要有一组准确的速度场，即可模拟其中的气泡动力学特性，实践表明，这种思想是可行的，并且可大大的节省时空复杂度。

1.1.2 基础模型

气泡群模型是尾流流场的气泡群聚并模型构建的重要基础，一个典型的波尔兹曼型气泡群平衡方程［10］:

式中:n(z，d，t)为与空间(z)、气泡尺寸(d)、时间(t)有关的单位体积气泡数密度函数;u是对应的(z)方向的气泡速度;d(z，d)为与空间(z)、尺寸(d)有关的表示气泡尺寸因气体传质而引起变化的函数;与气泡聚并和破裂有关的源项S(z，d，t)可以如下表示:

其中，

分别表示体积小于Vi的气泡与体积为(Vi-Vj)的气泡聚并为体积为Vi的气泡速率，气泡Vi与其它气泡聚并而导致气泡Vi消失的速率，体积为2Vi的气泡分裂产生两个气泡Vi的速率，气泡Vi本身分裂消失的速率。

与普通的波尔兹曼型输运方程［4］相比，气泡群平衡方程的优势在于不仅包含传质与扩散项，还包括聚并与分裂项，因此对于气泡群尺寸的分布与变化描述将更加精确，考虑到实际情况，尾流气泡尺寸太小几乎不会分裂，因此文中将忽略分裂的影响。下面将基于气泡尾流模型对方程(1)进行适当的化简和离散处理，使其可以用于对舰船尾流的数值模拟。

1.2 模型建立的相关求解

1.2.1 模型的化简和离散

首先建立尾流场二维坐标系，与航向平行的方向为x，垂直水面向下的方向为y。仅考虑气泡数密度在轴向x和竖直方向y的变化，空间项可以表示:

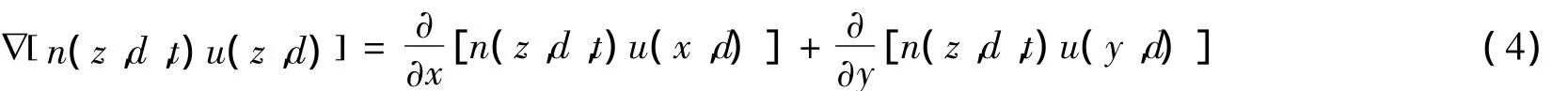
注意到以下两个关系式:

则有:

对于方程(1)中的扩散与传质，有:

由式(7)可知，时间项可以被消去，因此式(9)可以化简为:

其中，ψ(d)表征扩散与传质，是关于直径d的一元函数。

联立式(1)、(4)、(7)、(8)、(10)，且考虑到气泡尺寸小到可以忽略分裂项，最终得到如下模型:

气泡群平衡方程最终化为只与坐标x和气泡尺寸d有关的二维偏微分方程，在求解前需要对轴坐标x和气泡尺寸d进行离散化处理，采用差分法离散后的数值模型:

其中，n(i，j)表示x=iΔx处尺寸为d=jΔd的单位体积气泡数密度;u(i，j)表示x方向尺寸为d=jΔd的气泡速度。下面分别给出聚并模型Ω与传质模型ψ的求解。

1.2.2 聚并模型及其修正

体积分别为Vi和Vj的气泡集合聚并速率Ωc等于各自密度乘以碰撞概率乘以聚并概率］11］:

其中，碰撞概率θij等于湍流诱导的碰撞概率θijT加上浮力诱导的碰撞概率θijB。上述模型只适用于气泡数密度小的实验室水箱或鼓泡塔，而对气泡数密度巨大的尾流则无能为力，因为ninj后其结果之大完全可以超乎想象，导致碰撞的发生会远远大于实际存在的气泡数，这是与实际明显相悖的，为此，将其修改为:

湍流诱导的碰撞概率:

浮力诱导的碰撞概率:

聚并概率:

其中接触时间［11］:

聚并时间［11］:

上式思想来源于液膜排水模型，其中初始膜厚度h0=5×10-4，破裂液膜厚度hf=1×10-8。两气泡的特征尺寸dij:

1.2.3 传质模型

应用田恒斗［1］建立的舰船尾流气泡上浮传质模型:

其中，CA为海水中的气体质量浓度，CI为气液界面处的气体质量浓度。

当深度h固定时，对式(23)化简并对d求偏导即可得到ψ(d)的一元函数表达式。

2 计算与讨论

求解尾流场的流动参量的方法可采用MINER［5］提出的方法，在给定船型参数和附件参数(如船长、船宽、吃水、船速、螺旋桨盘面尺寸、桨轴位置等)的情况下，可近似得到尾流空间各点的初始速度、湍动能、湍动能耗散率。根据理论分析和测量经验，湍流尾流的速度发展变化可以用以下乘幂曲线近似表达［13］:

图1 模拟的尾流速度沿x方向的变化Fig.1 The change of simulated wake speed along x

其中，u0为初始尾流速度，k为待定系数(文中设为5.0)。使用上述方程拟合的尾流速度如图1所示。由图可知拟合曲线光滑、连续、稳定，与实际情形较为接近。

计算实例取文献［3］给出的美国某实船模型，其中各参数具体:船长为86.9 m，船宽为14.6 m，吃水3.6 m，船速为12节，螺旋桨直径2.44 m。为了进行数值计算，气泡尺寸需要按照大小进行分组，采用文献［7］的分组方法，如表1所示。

这样共得到15个相互耦合的差分方程组。由于要求解气泡群尺寸沿x方向的分布，又由于气泡的速度可以用流场速度U近似，因此有u(x，d)=U。模型将在普通台式机上运行，完整模型的运行时间不超过4 s，相对以往文献的数值模拟方法大大提高了计算效率，可以达到实时监测的要求。

表1 各组分气泡数密度的初始化Tab.1 Initialization of the bubble-group BND

2.1 沿尾流流向的气含量分布

首先对沿尾流流向的气含量分布特征进行求解分析。用于计算气含量的公式:

这里，由于差分步长Δx设为1 m，因此单位体积VL=1 m3，尾流中总的气含量表达式:

图2为只考虑传质、聚并及二者综合情形下的尾流中气含量沿尾流流向的分布。可以看出三种情形下的气含量总体分布均以乘幂形式进行衰减。相对于传质因素，聚并作用在近尾流区(小于1 800 m)更加明显，这是由于近尾流区的船壳、螺旋桨搅动、湍流等因素作用非常强烈，大大增加了气泡碰撞的几率，促进了聚并的发生，在聚并的影响下，气含量衰减曲线更显陡峭。当进入远程趋于静止的尾流区(大于1 800 m)后，气泡间的影响减弱，聚并作用不再明显，这时传质因素开始发挥主要影响，使得气泡含量继续以直线方式缓慢减少。

将完整模型的计算结果与文献［3］的实验数据进行对比，在比较前，需要将长度单位换算为时间(min)，近似为:

其中，L为尾流长度，U为船速。

此外，由于初始值不同，文中的结果大小会与文献［3］有所不同(相差约0.1)，因此，为了在同一幅图中比较，还需各自进行归一化，归一化后将文中计算结果与文献［3］进行对比，如图3所示。由于文献［3］的研究分为近程尾流(小于1 800 m)和远场尾流(大于1 800 m)，因此测量曲线没有连续，但仍可将其结果与文中气含量计算值的相应区间进行比较。由图可知文中计算结果与文献［3］中气含量实验结果曲线的走向吻合较好。

图4为文中计算的BND沿尾流流向分布与文献［4］的计算结果的对比。可以看出，虽然增加了考虑聚并因素，仍与文献［4］吻合较好，进一步表明了文中计算模型的有效性，同时说明聚并对BND的变化影响不大。

图2 气含量沿x方向的变化Fig.2 The change of air content with x

图3 气含量随时间的变化Fig.3 The change of air content with time

图4 气泡数密度沿x方向的变化Fig.4 The change of bubble BND with x

2.2 气泡尾流尺寸的相对分布

下面对气泡尾流不同尺寸的相对气含量及BND分布特征进行计算分析。图5是在分别考虑传质因素、聚并因素及二者综合情形下，位于尾流充分发展的远场尾流区(x=3 000 m)的不同尺寸气泡BND的相对值分布。由图可知只在聚并作用下的气泡数密度值与气泡尺寸成反比，这主要是由于大气泡在湍流诱导下的碰撞概率更高，因此聚并消失的速率更大，密度下降也最快。而在传质作用下，小气泡由于迅速溶解而消失，大气泡由于迅速上浮至水面破裂而消失，致使尺寸约为70～80 um的气泡数密度最大。根据以上结论，综合情形下的相对BND分布与只有传质影响下的相对BND分布区别不大。

图6是位于尾流充分发展的远场尾流区(x=3 000 m)的不同尺寸气泡气含量的相对值分布。由图可知尺寸200 um的气泡气含量最大，这与文献［7］针对气泡气含量相对分布的研究结论是基本一致的。与图5相比，可知对于只有聚并因素的情形，虽然小气泡的密度较大，但是由于体积较小，因此气含量就会相对变小(由表1也可明显看出)。同时可以看出虽然只在传质作用与综合情形下的气泡相对BND分布比较接近，但是二者气含量的相对分布却有较大差异，这说明聚并在气泡尾流的气含量分布与变化中发挥着主要作用，不能忽视。

图5 不同尺寸气泡相对数密度Fig.5 Relative BND of bubble with different dimensions

图6 不同尺寸气泡相对气含量Fig.6 Relative air content of bubble with different dimensions

3 结语

气泡尾流以其强大的制导作用而一直被各国军界作为研究的重点来对待，鉴于以往对气泡尾流特征参数的分布研究方面存在的不足，基于BPBE方程提出了可以同时将传质与聚并作用包含在内的用于气泡尾流特征分布研究的新思想，并使用数值方法对模型进行了仿真求解，分别对传质因素、聚并因素以及二者综合因素情形下气泡气含量以及BND的特征进行了分析研究，结果表明聚并在近尾流区作用强烈，而在远程尾流区传质起主要作用。聚并对BND的分布变化影响不大，但对气含量的影响则作用明显，不可忽视。模型大大提高了计算效率，达到了军事应用的实时性需求，且结果与相关文献及实验数据吻合较好，表明了该模型的有效性。

符合说明:ξ为湍动能耗散率;g为引力常数，10 m/s2;σ为表面张力，0.074 N/m;ρL为海水密度，1 200 kg/m3;Patm为标准大气压，105Pa;R为气泡半径，m;ρg为气体密度，1 kg/m3;vb为气泡上浮速度，m/s;DAB为气体扩散系数，1.8×10-9m2/s;v为流体粘度，0.001 kg/ms。

［1］ 田恒斗，金良安，迟卫.船舶远程尾流场中气泡上浮运动模型［J］.船舶力学，2010，14(11):1195-1201.(TIAN Heng-dou，JIN Liang-an，CHI Wei.Rising process model of bubble in the far wake of ship［J］.Journal of Ship Mechanics，2010，14(11):1195-1201.(in Chinese))

［2］ Stewart M B，Miner E W.Bubble Dynamics in a Turbulent Ship Wake［R］.NRL Memorandmm Report，6055，1987.

［3］ 陈圣涛，王慧丽，王运鹰，等.舰船气泡尾流特性的数值模拟和实验研究［J］.船舶力学，2012，16(4):342-349.(CHEN Sheng-tao，WANG Hui-li，WANG Yun-ying，et al.Numerical simulation and experimental study of a ship's bubble wake［J］.Journal of Ship Mechanics，2012，16(4):342-349.(in Chinese))

［4］ 朱东华，张晓晖，顾建农，等.舰船尾流及其气泡数密度分布的数值计算［J］.兵工学报，2011，32(3):315-320.(ZHU Dong-hua，ZHANG Xiao-hui，GU Jian-nong，et al.Numerical calculation of ship wake and its bubble number density distribution［J］.Acta Armamentarii，2011，32(3):315-320.(in Chinese))

［5］ Miner E W，Ramberg S E.Method for Approximating the Initial Data Plane for Surface Wake Simulation［R］.US:RL-MR-6376，1988.

［6］ 刘慧开，张劝华，杨 立.海洋表层气泡运动规律的研究［J］.海洋科学，2009，33(1):34-38.(LIU Hui-kai，ZHANG Quan-hua，YANG Li.The study on the motion of bubbles near the ocean surface［J］.Marine Sciences，2009，33(1):34-38.(in Chinese))

［7］ Carrica P M，Drew D，Bonetto F，et al.A poly disperse model for bubbly two-phase flow around a surface ship［J］.International Journal of Multiphase Flow，1999，25(2):257-305.

［8］ 高 江，张静远，杨 力.舰船气泡尾流特性研究现状［J］.舰船科学技术，2008，30(4):27-32.(GAO Jiang，ZHANG Jing-yuan，YANG Li.The present situation of research on shipwake characteristic［J］.Ship Science And Technology，2008，30(4):27-32.(in Chinese))

［9］ Smimov A，Celik I，Shi S.LES of bubble dynamics in wake flows［J］.Computers＆ Fluids，2005(34):351-373.

［10］Ryszard P W，Moniuk W l，Bielski P，et al.Modelling of the coalescence/redispersion processes in bubble columns［J］.Chemical Engineering Science，2001，56:6157-6164.

［11］Prince M J，Blanch H W.Bubble coalescence and break-up in air-sparged bubble columns［J］.A.I.Ch.E.Journal，1990，36(10):1485-1499.

［12］徐麦容，刘成云.水中浮升气泡的半径和速度变化［J］.大学物理，2008，27(11):14-17.(XU Mai-rong，LIU Cheng-yun.The change of radius and velocity of the rising bubble in water［J］.College Physics，2008，27(11):14-17.(in Chinese))

［13］James K E，John R D，Brian A M.The radar image of the turbulent wake generated by a moving ship［J］.London Research and Development，1993，755:343-346.