基于最小二乘法的弦振动的研究

张松锋　张鸿辉　周小东

摘要：弦振动的研究是大学物理实验中研究驻波的经典例子，对实验数据的处理一般都是利用Origin软件进行，用最小二乘法对数据进行处理比较少见。 本文利用最小二乘法对实验数据进行处理，并用Origin进行线性拟合，结果表明：弦上横波波长的对数和弦线张力的对数成线性关系，和Origin拟合结果相符；利用两种方法计算波速时，误差很小，只有质量在120g时误差稍大，但也在允许的范围内；振动的实际频率和理论频率和波速误差相似。

关键词：弦振动；最小二乘法；Origin；波速；频率

中图分类号：TP391 文献标识码：A文章编号：2095-2163（2015）06-

Abstract： String vibration research is the classical example of a standing wave in university physics experiment， the experimental data processing are generally using Origin software， using least square method are relatively rare. This paper using least square method to deal with the experimental data， and linear fitting with the Origin， the results showed that a linear relationship with logarithm of wavelength and string tension，whichagrees with Origin fitting results； Using two methods to calculate the wave velocity， the error is very small， only at 120 g larger quality， but also in allowed range； The error of actual frequency and theoretical is similar with wave velocity.

Keywords： String Vibration；Least Squares Method； Origin；Wave Velocity； Frequency

0 引言

物理学的几乎每一个领域都涉及到波动的研究。 不同性质的波动传播机制虽然各异，但却具有共同的规律性，这种规律性可以用统一的数学表达式来进行提炼和呈现，所区别之处则在于数学公式中各个量所代表的物理意义不同[1]。物理学中有关波动的论述，大多以弦线上的驻波为例[2]。弦振动的研究是大学物理实验中研究驻波最典型的例子，是帮助学生理解波的形成、传播和干涉的一个重要实验[3]。

基于当下成果的研究分析可知，很少有采用最小二乘法处理弦振动实验数据的。 本文利用最小二乘法对实验数据进行了处理，研究了弦上横波的波长与弦线张力的关系，并与Origin拟合结果进行了对比， 对波速和频率及其误差也进行了计算。

1 实验原理[1，4-5]

将细弦线的一端固定在电振音叉顶端，另一端绕过一个位置固定的滑轮悬挂砝码。 当电振音叉以固有频率f0振动时，适当调节细弦线的长度l，沿细弦线会产生一列向前传播的横波，横波的振动频率亦为f0，当横波沿细弦线传播到滑轮处时会产生一列反射波，此反射波的频率、振幅与原波完全相同，原波与反射波在细弦线上发生干涉，实际在细弦线上观察到的是两列波相干涉叠加以后的波形。 当l正好等于弦上横波半波长的整数倍时，即：

利用（4）式计算弦振动时的实际频率，与理论频率进行比较.

2 实验内容及原始数据记录

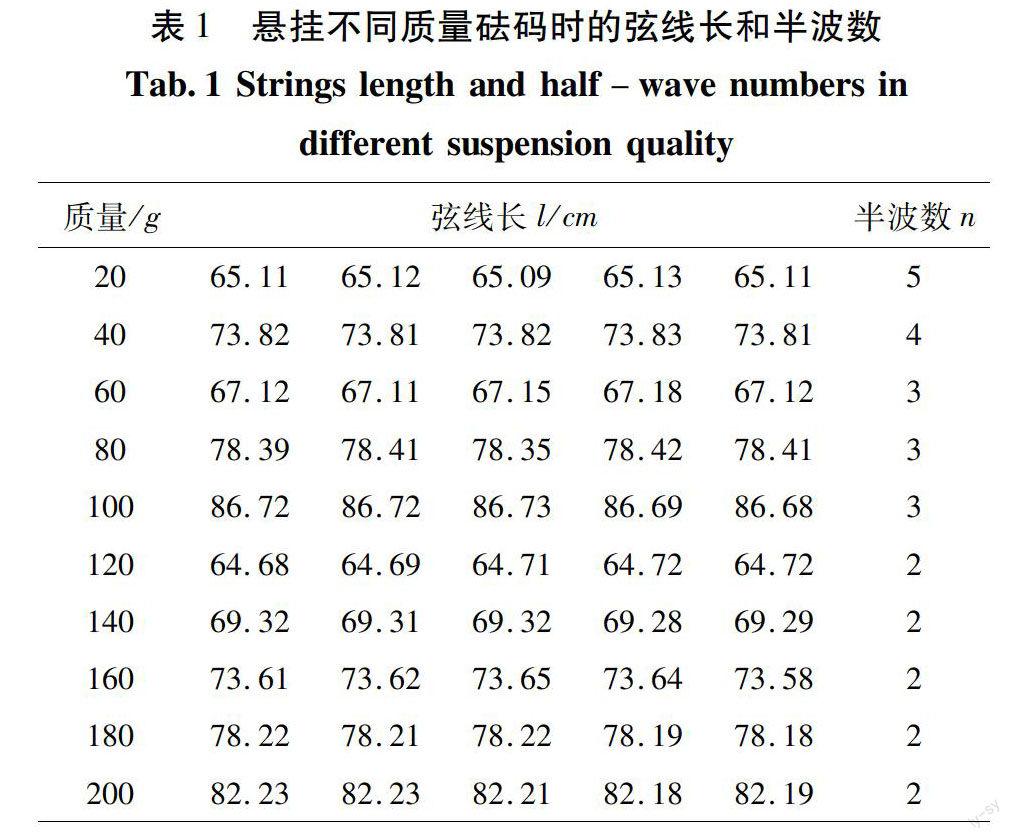
将砝码质量依次取为20g、40g、60g、80g、100g、120g、140g、160g、180g、200g，调节细弦线的长度l，使弦线上出现振动情况稳定的驻波，记录半波区的个数n值，用米尺测量l大小，测量5次，数据如表1所示。

3 数据处理及结果分析

3.1 验证波长与张力的关系

根据实验原理中所述公式，计算波长λ、lnλ和lnFT，如表2所示。

3.1.1 最小二乘法處理数据

根据最小二乘法处理数据的原理，设直线方程为y=a+bx，通过计算得出b=0.501169，a=-0.52878，关联系数γ=0.999855。Eγ=0.0145%，Eb=0.2338%. 从结果上看，关联系数接近于1，说明lnλ、lnFT具有良好的线性关系，b的数值和理论值1/2的误差仅为0.2338%，在误差允许的范围内，说明实际值和理论值符合得较好。

3.1.2 Origin软件处理数据[5]

打开Origin软件后，界面上会出现两列空白数据表格A（X）、B（Y），分别输入表2中的lnFT和lnλ，以lnFT作为横坐标X的数据，lnλ作为纵坐标Y的数据，通过Origin软件进行线性拟合，结果如图1所示，拟合报告如表3所示。

从图1和表3中可以看出实际曲线和拟合曲线具有贴切良好的跟随性，更加印证了lnλ和 lnFT是线性关系。 这和利用最小二乘法算出的结果是一致的。

3.2 波速和振动频率的计算

利用（2）式计算V，利用（3）式计算V？，利用（4）式计算f，并计算EV和Ef，其中f0=100Hz。计算结果如表4所示。

利用Origin软件作m-EV图和m-Ef图，分别以m为横坐标，EV和Ef为纵坐标. 如图2、图3所示。

从表4和图2、3中可以看出，两种方法计算波速的误差大部分都在1%以内，最低达到0.00878%，只有质量在120g时出现大于1%的情况，频率的误差和波速的误差相似。 另外不同质量下EV和Ef几乎相等，也很好的印证了两种计算方法得出的结果是一致的. 即如果令V？=λf，EV的比值就是Ef的比值。

4 结束语

本文用最小二乘法对弦振动的实验数据进行了处理，并用Origin对lnλ-lnFT进行线性拟合，计算结果和线性拟合结果呈现出优质的现实一致性，得出lnλ、lnFT具有良好的线性关系；用两种方法计算波速，误差大都在1%以内，当质量在120g时误差较大，但也在允许范围内；频率的误差和波速的误差相似。

参考文献：

[1] 吴定允，常加忠. 大学物理实验[M]. 河南：河南科学技术出版社，2014：134-138.

[2] 赵艳，王春兴. 弦线上的驻波研究[J]. 山东师大学报：自然科学版，2000，15（3）：320-321.

[3] 苗锟，黄育红，李康等. 弦振动形成驻波的规律和数据的MATLAB处理[J]. 大学物理实验，2010，23（4）：75-79.

[4] 崔群. “弦振动的研究”实验强化偏微分方程的感性认知[J]. 鞍山师范学院学报，2014，16（6）：21-26.

[5] 李生仁，白琼燕，杨军等. 利用Origin分析弦振动形成驻波的规律[J]. 科技创新，2014，2月（上）：191-193.