求解旅行商问题的动态邻域差异演化算法改进研究

刘永军　孔佑琳

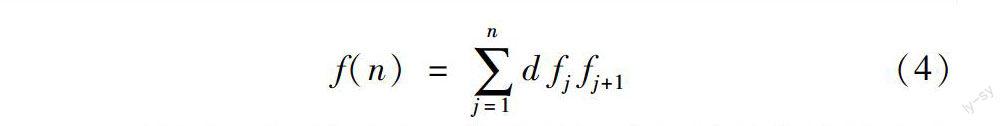
摘 要：旅行商问题（Traveling Saleman Problem，TSP）是一个典型的组合优化问题，针对该问题主要采用动态规划和智能优化等算法。为了有效求解TSP问题，设计了一种带邻域操作的差异演化算法。为了克服差异演化算法容易收敛于局部最优的弱点，通过引入簇和邻域的概念，将种群中的个体归入距离其最近的子种群，用个体的当前邻域极值替换群体的当前最佳。同时，算法在进化过程中动态调整邻域大小。通过在多个TSP问题的上的仿真实验表明，该算法在求解TSP问题时鲁棒性强，求解精度高。

关键字：旅行商问题；差异演化；动态邻域搜索；自适应

中图分类号：TP391 文献标识码：A 文章编号：2095-2163（2015）06-

Abastract：Traveling Saleman Problem is a classical Combinatorial Optimization Problem. Dynamic design and intelligence optimization are usually used to solve it. In order to overcome the differential evolution algorithm converges to a local optimum easily weakness by introducing the concept of clusters and neighborhood， the population of individuals classified as its nearest sub-population groups， and replace the current individual neighborhood the most good.. At the same time with extreme values，the number of neighborhood is adjust from two to the size of population. Some experiments on classical TSP problem show that this improved DE algorithm is effective and robust to solve TSP and has higher precision.

Keywords：TSP； Differential Evolution； Dynamic Neighborhood Search； Self- adaptive

0引 言

旅行商问题（Traveling Salesman Problem，TSP）源于EULER提出的骑士旅行问题，在我国又被广泛称为“货郎担问题”、“邮递员问题”等，是计算机科学、管理学、运筹学中的一个重要内容，属于典型的组合优化范畴。Gaery通过理论方法证明了该问题是一个典型的NP难问题。由于NP难问题具有一定的类归属和研究成果扩展性，在TSP问题上取得的理论或者实验成果，可以用于指导求解其它的NP难解问题，又由于TSP问题具有形式简单、易于描述的特点，在组合优化问题中具有一定的代表性，因此该算法经常被用于作为研究组合优化的典型实验和验证平台，而获得了学界多方广泛且深入的研究。

TSP问题的研究具有非常广泛的工程应用背景和学术研究价值，在工程领域中非常多的工程问题其实质就是TSP问题，亦或可以转换为TSP问题，如：网络通讯、电路板钻孔、交通调度、管道铺设、电网规划等等，因此，快速、有效地实施对TSP问题的研发处理将会具有较高的实际应用价值。

为了有效求解TSP问题，文献[1]针对萤火虫算法的特点，提出了一种离散型萤火虫算法，针对TSP问题专门设计了算法的更新方式、种群初始化方式、个体的编解码方式，为了增强算法的局部搜索能力，加快其收敛速度， 在算法中使用了2-opt优化算子。通过实验显示，该算法的求解要较自适应萤火虫算法具有更高的执行精度；文献[2]通过研究蚁群算法的特点，提出了蚁群算法求解TSP问题的方案，并令蚁群算法根据启发函数 信息素进行算法性能优化，提高了算法的收敛速度；文献[3]同样利用蚁群算法来求解TSP问题。在该论文中，针对蚁群算法容易早熟的弱点，算法中引入“优胜劣汰”的进化策略，对每次迭代的随机进化因子大于进化漂变阈值的路径信息素进行二次更新，加快算法的收敛速度；同时利用随机进化因子的增强算法跳出局部最优解的概率基础，得到相对优化的问题求解；文献[4]提出了应用遗传算法求解TSP的方案。初始种群使用贪婪机制来构造，并使用融合轮盘赌方法和最佳保存策略进行选择操作，针对交叉操作则应用两点三段随机交叉的方法。

文献[5]采用遗传算法和文献[6]的基本邻域机制以及文献[7-8]的差分演化思想，为TSP问题求解提出了较好的思路和方法，为了更有效的求解TSP问题，本文设计一种基于动态邻域机制的差异演化算法求解TSP问题。给出了差異演化算法的编码机制，并定义了算法中个体之间的距离和邻域等概念，通过在差异演化算法中引入个体邻域的概念，用个体当前的邻域极值替换种群的全局极值，保证种群多样性，提高算法全局收敛能力。

1 TSP模型和差异演化算法

定义1 存在n个结点 ，任意两个结点之间都存在直接的路径关联，对于任意两个结点 之间的消耗为 。假定从其中任意的某一个结点 出发，每一个结点只能经过1次，在经过全部的结点之后重新回到 ，消耗的费用是 。问如何规划一条合适的路径 ，使 的值最小，并确定该最小值。

定义2.组合优化问题 ，存在两个决策向量 ，定义这两个决策向量之间的距离为不同时属于 和 的元素的个数，即：

2 求解TSP问题的动态邻域差异演化算法

2.1个体编码方式

根据TSP问题的描述，采用整数编码机制。将鱼群的个体设置为长度30的整数串，代表了一个循环长度。例如：某个体编码为（3-20-18-9-0-1-2-5-……16），则代表从节点3开始依次经过节点20、18、9、0、1、2、5…16，形成一条路径。

2.2适应度函数的设计

显而易见，采用如下公式：

描述最短路径是最直接的表达方式。TSP问题的目的就是求解公式（4）的最小值。

2.3种群初始化方式

鉴于所求问题为最短路径，所以种群内的个体模式表达两个城市之间的距离越短，对于后续的寻优工作就会更加有利。为此，本文依据两个城市间的距离，利用轮盘赌的机制来初始化种群，这一方式使得种群中所包含的解已经比较接近最优解。

2.4 动态邻域差异演化算法

由于差异演化算法的趋优性，在后期个体往往容易聚集于局部最优个体的周围，使算法趋于早熟。为了克服原始差异演化算法的这一弱点，在运算过程中有必要依据一定的标准对群体或部分个体进行再组织，以维持种群的多样性。文献[3]中有Kennedy为粒子群算法提出了一种新的组织结构，该结构增加了空间邻域和环形拓扑方法，称为social stereotyping，作者设计了确定搜索空间的粒子簇的方法，并通过实验证实了如果使用该粒子所在簇中心值替换个体最优值将会提高算法的性能。围绕这一思想，同样将邻域机制引入差异演化算法，来指导差异演化算法的收敛过程。针对求解TSP问题，将差异演化算法中涉及的数个概念定义如下。

定义3个体距离 根据TSP问题的描述以及定义2，设图 中具有顶点 个，则定义个体表达模式为 ，如果任意两个结点 之间存在连接通路，则定义差异演化算法中个体之间的距离 为 之间互不相同的边的数目。

据此定义，若存在三个个体 ，则可得到如下定理。

定义4 对于组合优化问题 ，定义 为 的 邻域， 称为 的邻居。

由以上定义3、4可对TSP问题搜索空间的邻域得到相应定义如下：

定义5.设差异演化算法中某个体 代表一个TSP问题的一个特定解，其 邻域定义为 ，并且， 为大于或等于2的整数。由此可知，在求解TSP问题中，某个个体 的邻域集合应该是包含种群中所有与 互不相同的边数小于或等于2r的个体。

定义6 对于TSP问题某个解 ，如果 且 ，则环路 是邻域 的局部最优解。

根据上述的簇定义和距离等的定义，可知在带有邻域操作的差异演化算法中，可将此时最佳使用群体中个体的当前邻域极值进行替换。取邻域值，在该邻域内随机抽取一个解 ，使用邻域差异演化算法搜索到问题的局部最优解 ，则 ，若 ，将 更新为 ，重复此过程；若 ，说明尚未找到比 更优解，重复搜索。

为了提高差异演化算法的搜索能力，参考文献[9]，将其参数F、CR修改为自适应调整方式，公式为（5）、（6）。

这里的 为均匀分布在[0，1]上的随机数， 为其上界值， 为其初值。

算法2 动态邻域差异演化算法（DNDE）

Step1 在解空间内随机初始化m个个体组成一个种群，并设定最大迭代次数为Maxiter；

Step2 设置算法的各个参数，个体当前邻域范围 ；

Step3 计算全部个体的适应度值；

Step4 对于种群中所有的个体 ，设其邻域内局部最优为 ，如果 ，则用 更新 ；

Step5 设当前种群最佳 ，对于种群中所有的个体 ，如果 ，则用 更新 ；

Step6 根据定义动态改变邻域范围， ，至种群最大维数为止；

Step7 执行交叉、变异、选择操作；

Step8 利用公式（5）和（6）调整F和CR；

Step9 如果满足结束条件，则输出最终结果，结束程序；否则返回step3。

3 仿真实验与分析

为了验证算法的有效性，采用C语言进行编程，并在开源软件Code：：Block上进行了实现。DNDE算法参数设置为：种群规模100， ， ，CR=0.6，选择两侧的两个相邻个体为临近个体。算法的最大迭代次数为3 000次。

3.1仿真实验1

首先针对Burma14、Ol iver30、Ei l51三个算例进行实验对比，将DNDE算法运行20次，并与文献[1]提供的两个算法DGSO与 SAPSO进行对比，实验结果列于表1。从表1 的实验数据可以看出，对于14个点的TSP问题，DNDE算法与文献[1]的两个算法取得的结果是一样的，20次全部得到最短的路径。而对于30个结点的Oliver30问题，DNDE算法同样能够完整得到当前已知的最佳解，与DGSO是一样的，但比SADPSO的解要更加优质。而在51个结点的Eil51问题上的求解上，差异演化算法的高效性在此得意清晰展现，求得的结果与文献[1]的算法相比则具有显著优越性。

3.2仿真实验2

为了更好地验证DNDE算法的计算效率，另外选取了其它的5个TSP问题，再将本算法运行20次，并与文献[2]提供的优化ACO算法进行对比，实验结果列于表2。从实验结果对比分析可以看出，本文所提出的NDDE算法在5个典型的TSP问题上，无论是最优解、最差解还是平均解方面都明显胜出于优化的ACO算法。从表2列出的DNDE算法平均解可以看出，该算法的平均解更接近于最佳解，说明算法运行20次所获得解之间的离差比较小，算法稳定性较高。

4 结束语

针对TSP问题的特点，定义了差异演化算法的編码方式、适应度函数以及种群距离等，提出了一种求解TSP问题的改进差异演化算法。在此基础上，为了提高该算法的全局收敛能力，引入了簇的概念和邻域机制，从而使算法的后期仍然能够较好的保持种群多样性。本次研究和设计在多个典型TSP问题中的仿真实验表明，该算法求解精度较高、鲁棒性强。

参考文献：

[1] 周永权，黄正新，刘洪霞.求解TSP问题的离散型萤火虫群优化算法[J]，电子学报，2012，40（6）：1164-1170.

[2] 夏小云，李云浩，汪峰. 基于蚁群优化算法的TSP问题求解[J]， 江西理工大学学报，2009，4（8）：37-39.

[3] 吴华锋，陈信强，毛奇凰等.基于自然选择策略的蚁群算法求解TSP问题[J]，通信学报，2013，4（4）：165-170.

[4] 周泽岩，张喜. 基于改进遗传算法的TSP问题求解的研究[J].物流技术，2012，31（9）：220-223.

[5] ITOH H. The method of solving for travelling salesman problem using genetic algorithm with immune adjustment mechanism [A].Traveling Salesman Problem， Theory and Applications[C]. Switzerland：Intech Press， 2010：97- 112.

[6] DAS S，ABRAHAM A， et al.Differential evolution using a neighborhood- based mutation operator[J].IEEE Transactions on evolutionary computation，2009，13（ 3）： 526 -553.

[7] 张大斌，杨添柔，温梅.基于差分进化的鱼群算法及其函数优化应用[J]，计算机工程，2013，39（5）：18-22.

[8] 王永皎.改进自适应差分进化算法求解大规模整数任务分配[J]，计算机应用，2012，32（ 8） ： 2165-2167.

[9] 王培崇，钱旭. 基于改进鱼群算法的路径测试数据生成[J]，计算机应用，2013，33（4）：1139-1141.