对一道教材练习题的思考

张永静

【摘要】教材内容设置看似简单，注重基础，但是教材内容所涵盖的深邃内容需要研究发掘，进行拓展，才能够拓展学生思维，提高学生的综合素质和能力，如果引导学生进行深入思考，得出一些有价值的东西，既可以提高学习兴趣，又能够为后续学习提供更多的理论基础。

【关键词】源泉  探索  等积分形

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2015）08-0103-01

教材是学生学习的源泉，我们应该抓住其精髓，比如对一些习题，如果能够进行细致的思考，经过探索，会发现别有一番洞天。如果引导学生进行深入思考，得出一些有价值的东西，既可以提高学习兴趣，又能够为后续学习提供更多的理论基础。义务教育课程标准实验教科书《数学》八年级（下）第86页有这样一道练习题：

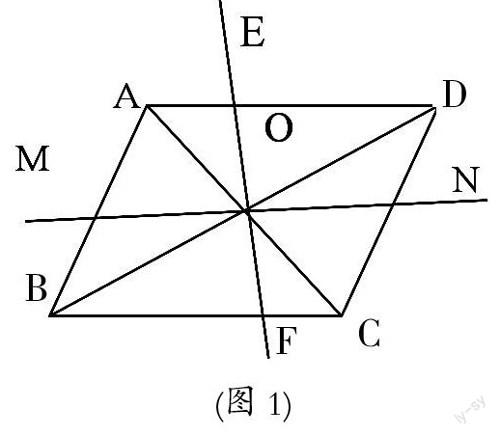
已知：如图1，？荀ABCD的对角线AC、BD交于点O，直线EF过点O且分别交AD、BC与点E、F，求证：OE=OF

該题证明过程如下：

证法一（证三角形全等）：

∵四边形ABCD是平行四边形

∴∠EAO=∠FCO，OA=OC

在△OAE和△OCF中

∠EAO=∠FCO

OA=OC

∠AOE=∠COF

∴△OAE≌△OCF

证法二：（用中心对称性质证之）：

∵？荀ABCD是中心对称图形

∴点E关于点O的对称点必在BC上

又∵点E关于点O的对称点在直线BF上

∴点E关于点O的对称点是直线BC与直线BF的交点

即点E关于点O的对称点是点F

∴OE=OF

根据证法二做进一步思考可得：

①点A与点B关于点O对称，点C与点D关于点O对称，点E与点F关于点O对称，故而四边形ABFE与四边形CDEF关于点O对称。

②由①根据中心对称性质可得四边形ABFE全等于四边形CDEF，故而有S四边形ABFE=S四边形CDEF。

综上所述可得：直线EF将？荀ABCD分为面积相等的两部分。

思考：如图1，直线MN是否也将？荀ABCD分成面积相等的两部分呢？

答案是肯定的，我们可以仿照上述过程证得直线MN将？荀ABCD分成面积相等的两部分，这里不再赘述。

由于直线EF与直线MN具有任意性，综上所述可得：

经过平行四边形对角线交点的任一直线把该平行四边形分成面积相等的两部分（等积分形）。

我们可以利用这一结论将梯形用一直线分成面积相等的两部分。其思路是将梯形转化为与其等面积的平行四边形，再利用上述结论将其分成面积相等的两部分。

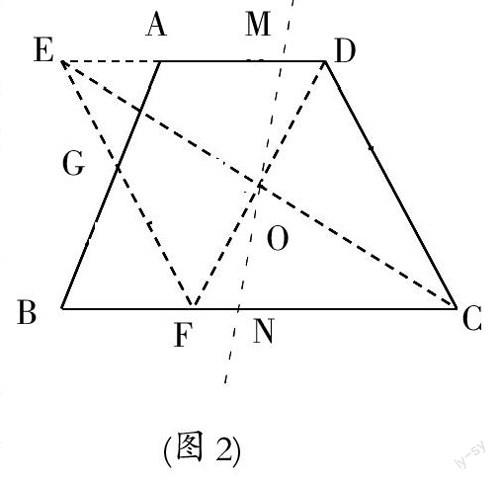
如图2过梯形ABCD一腰AB的中点G，作EF∥CD交BC于F，交DA的延长线于E，则△AEG≌△BFG，从而有

S梯形ABCD=S？荀EFCD，连接CE、DF交于点O，再过点O作一直线MN，使之与梯形两底AD、BC分别交于点M、N，则S四边形MNCD=S四边形NMEF，由于△AEG≌△BFG，进而可以说明S△AGE+S五边形AGFNM=S△BGF+

S五边形AGFNM，即S四边形NMEF=S四边形MNBA，故而S四边形MNCD=S四边形MNBA.

这样我们可以成功地将梯形ABCD分成面积相等的两部分。

由此看来，只要引导学生善于思考，经过探索研究，可以不断地从教材中汲取营养，踏进更加美妙的数学殿堂。