导引头跟踪点跳变对制导精度影响分析

中国空空导弹研究院 马 刚 梁雯洁

在导弹末制导过程中，跟踪点位置的跳变会导致制导性能的下降。例如对于雷达制导体制进行双目标攻击，在角度门分辨出目标时，会发生跟踪点位置的变化；对于红外制导体制末端抗干扰时，干扰与目标分离过程，也会引起跟踪点位置的变化。本文重点分析跟踪点跳变对制导系统的影响及最终脱靶量与各参数之间的关系，如跟踪点位置变化量、弹体制导时间常数、剩余飞行时间、有效导航比系数等。

1 跟踪点位置变化对制导系统影响分析

1.1 简化理想动力学模型闭合解

使用简单的线性模型来分析，假设弹体环节为理想环节，导引头测量无延迟、噪声等，建立的简单线性化模型如图1所示[1]。图中，Vc为相对速度，tgo为剩余飞行时间，N′为有效导航比，λ为视线角，y(tF)为脱靶量，tF为飞行时间。

图1 简化理想制导回路Fig.1 Ideal guidance loop

假设目标不机动，仅分析目标跟踪对象位置变化ymyt对脱靶量的影响。在目标不机动、目标无指向误差等情况下，弹目相对机动可以描述为：

对上式一次积分得到：

式中，C1是积分常数。

将视线角λ表达式代入公式(2)，得到线性时变一阶微分方程：

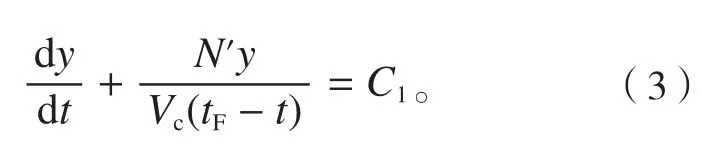
可以求解相对轨迹的微分方程闭合解，对于目标位置突变，可以认为初始条件

根据公式可以求取脱靶量、控制指令与时间的关系：

可见，当假设制导系统无滞后、纯理想环节的情况下，脱靶量恒为零。由公式(6)可以得到，过载指令的需求与位置突变的大小成正比，与飞行时间的平方成反比。

1.2 弹体环节为一阶惯性环节闭合解

根据1.1节可以得到，若制导系统具有足够的机动能力及无动力学环节的情况下，则脱靶量肯定衰减到零[2]。进一步将所有动力学环节集成一个惯性环节[3]，具有惯性时间常数T，模型框图如图2所示。

图2 一阶滞后制导系统Fig.2 First-order lag guidance system

对上述系统进行转换，将两个积分环节移到系统输入之前，变换后系统框图如图3所示。

图3 变换后的系统框图Fig.3 Alternated system block diagram

其中

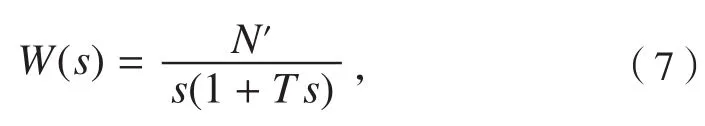
构建伴随系统(见图4)，并进行变换。

图4 伴随系统构成图Fig.4 Adjoint system bolck diagram

根据图4，利用卷积公式，有：

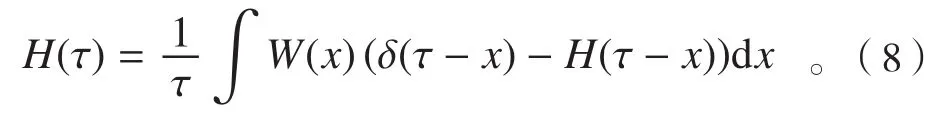
对式(8)进行拉斯变换，从时域变换到频域[4]，得到：

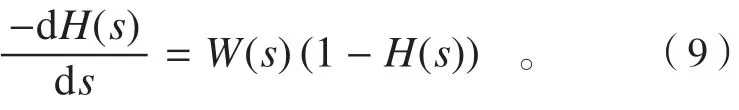
采用变换方法，得到：

根据公式(7)，求得：

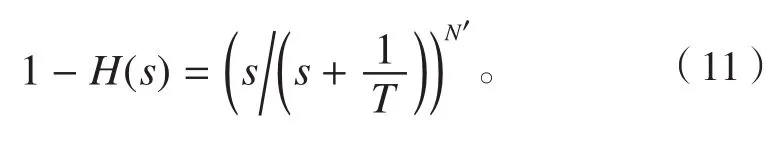
根据框图，可以求解得到目标单位位移造成脱靶量的响应(频域)：

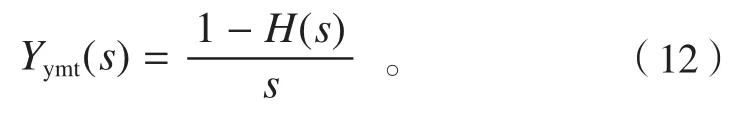
根据公式(11)、公式(12)求得脱靶量与飞行时间、位置突变量之间的关系：

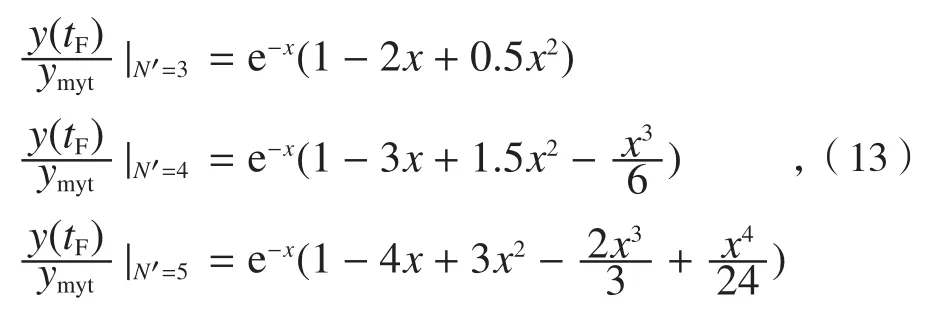
式中，x=tF/T 。

脱靶量与跟踪点变化大小、剩余飞行时间、制导时间常数等之间的归一化曲线如图5所示。

图5 制导系统一阶惯性环节脱靶量归一化曲线Fig.5 Miss distance normalization curves of first-order lag adjoint system

1.3 实际动力学环节的仿真分析

与1.2节相同，仅将制导系统动力学环节变换成实际的情况，具体参数为：相对接近速度1000m/s,制导滤波器时间常数0.1s，导引头时间常数0.0216s，弹体频率30rad/s,阻尼系数0.7，导引头测量噪声0.0015rad，得到跟踪点变化所导致的脱靶量影响曲线，如图6、图7所示。

由仿真曲线可以看出：

(1)若无噪声、扰动存在的情况下，剩余飞行时间是制导时间常数的5倍以上时，脱靶量收敛到零。

图6 有测量噪声情况下跟踪点变化对脱靶量影响Fig.6 Effects of trackpoint changing on miss distance with measurement noise

图7 无测量噪声情况下跟踪点变化对脱靶量影响Fig.7 Effects of trackpoint changing on miss distance without measurement noise

(2)有效导航比越大，位置突变的影响越大。

上述仿真结果可以支持抗干扰情况下有效导航比降低对制导精度有好处的结论。考虑到跟踪过程导引头测量噪声和其他扰动因素，跟踪点变化引起脱靶量的结果会更为恶劣，但是分析的结论能够定性地描述跟踪点变化对脱靶量的影响。

2 跟踪点变化影响的抑制

由前文的分析结果可以看出，由于跟踪位置的突变而导致制导系统中视线角的瞬变会对制导精度造成不利影响。为了探讨制导系统对跟踪点变化影响的抑制策略，假设剩余飞行时间已知，当导引头探测到跟踪位置突变，制导系统可将其当作缓变信号处理。这时导引头不是即刻跟踪上目标，而是缓慢变化，视线角跟踪不是阶跃输入而是线性变化或以二次抛物线变化。

视线角的变化使用斜坡信号或抛物线信号处理，跟踪目标位置变化可以表示为：

或

式中，t=0表示跟踪目标位置变化的时刻，tF为遇靶时间。

由图8可以看出，在相同导航比和目标位置变化条件下，不同处理策略对末制导精度具有不同的影响特性。当采用阶跃变化时，所引起的脱靶量振荡大，收敛慢；当采用抛物线变化策略时，虽然较快地收敛到零附近，但是初始段下降较慢；采用线性变化策略，在大约0.3s以后，影响系数可以收敛到0.2以内。综合仿真结果可以得出，采用线性变化策略最为有效。

图8 跟踪策略对制导精度影响的分析Fig.8 Analysis of effects of different methods on guidance precision

3 结论

本文首先采用不同模型分析了跟踪点变化对制导系统精度影响，得出脱靶量的大小与跟踪点位置变化量、制导时间常数、剩余飞行时间等有关系。分析得出末制导过程中跟踪对象的变化对制导系统精度有较大的影响，特别是在弹道末端，剩余时间较小时影响更为剧烈；减小有效导航比可以降低对象位置的变化对制导系统带来的影响分析；最后讨论了抑制跟踪对象变化对末制导系统精度影响的策略。分析仿真表明，采用跟踪位置线性变化的方式可以有效抑制影响。

[1] 彭绍雄，王海涛，安进，等. 基于统计线性化伴随法的导弹制导系统精度分析. 飞行力学，2014(1): 43-47.

[2] 蒋瑞民，周军，郭建国.导弹制导系统精度分析方法研究.计算机仿真，2011(5)： 76-79.

[3] 毕开波. 飞行器制导与控制及其仿真技术. 北京: 国防工业出版社，2009.

[4] Paul Z. Tactical and strategic missile guidance (sixth edition).American Institute of Aeronautics and Astronautics,Inc,2012.