大偏载情况下双马达同步驱动控制建模及研究实现

中国人民解放军91336部队 徐东东 孙志朋 韩红斌 刘少强

液压传动系统由于具有结构轻巧、传动比大、运行平稳、有效防止过载，易于实现无级调速和自动化、自动控制及远距离操纵等显著优点，在科研实验室、武器装备、工程机械中广泛应用[1]。三轴飞行姿态液压仿真转台是由外框、中框和内框组成的一种高精度的试验设备，在航空、航天等军工行业有着广泛的应用。不论是卧式还是立式液压三轴飞行仿真转台，在其结构设计中，为减轻其框架重量，缩小液压马达的结构尺寸，增加框架组件的结构强度，提高转台总体的动静态性能指标，大多数转台的中框架或外框架会采用双液压马达同步驱动方式。因此，双马达同步驱动技术就成为三轴液压飞行仿真转台研制中的一个关键技术[2-3]。

1 双马达同步控制系统建模

三轴飞行仿真转台电液位置伺服系统控制精度和动态特性都要求较高[4]，而且对于某型三轴液压仿真转台，由于特殊的应用需求，内框滚动轴系为中空液压马达结构，整个偏离俯仰轴线10多厘米，造成俯仰轴偏载较大，提升了同步控制难度。

对于以中空液压马达为负载的双马达同步控制系统，同步的一个重要目标是要使系统运动时中空液压马达的变形达到最小，从而避免中空液压马达因为变形导致泄漏加剧、卡死等故障的发生[5]。

为了直观地考察双马达同步系统负载的变形，建立如图1所示简化的单弹簧双惯量系统模型。

参照文献[6]阀控中空液压马达系统的建模过程，得到两阀控马达的数学模型如下：

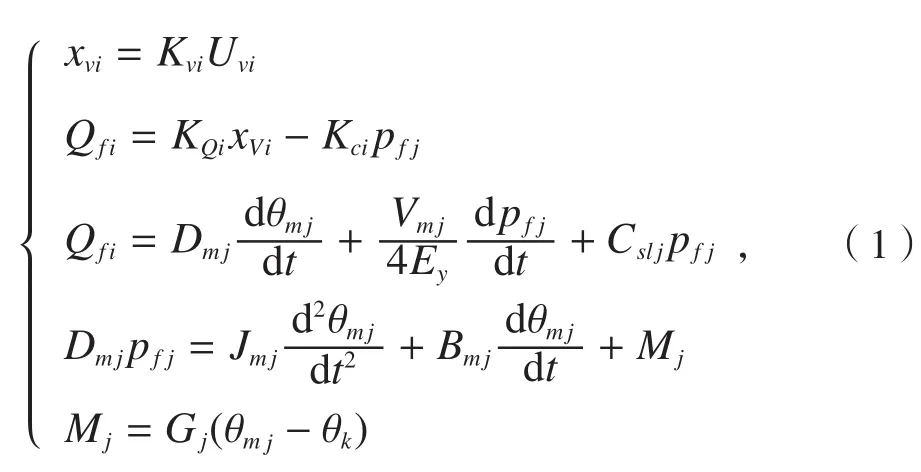
式中，Uvi、xvi、Qfi分别为伺服阀 i的输入信号、阀芯位移与输出流量；θmj、pfj、Mj分别为阀控马达j的角位移输出、负载压力与输出扭矩；θk为惯量块k的角位移，其余符号参照表 1，i，j，k=1，2。

负载的动力学模型为：

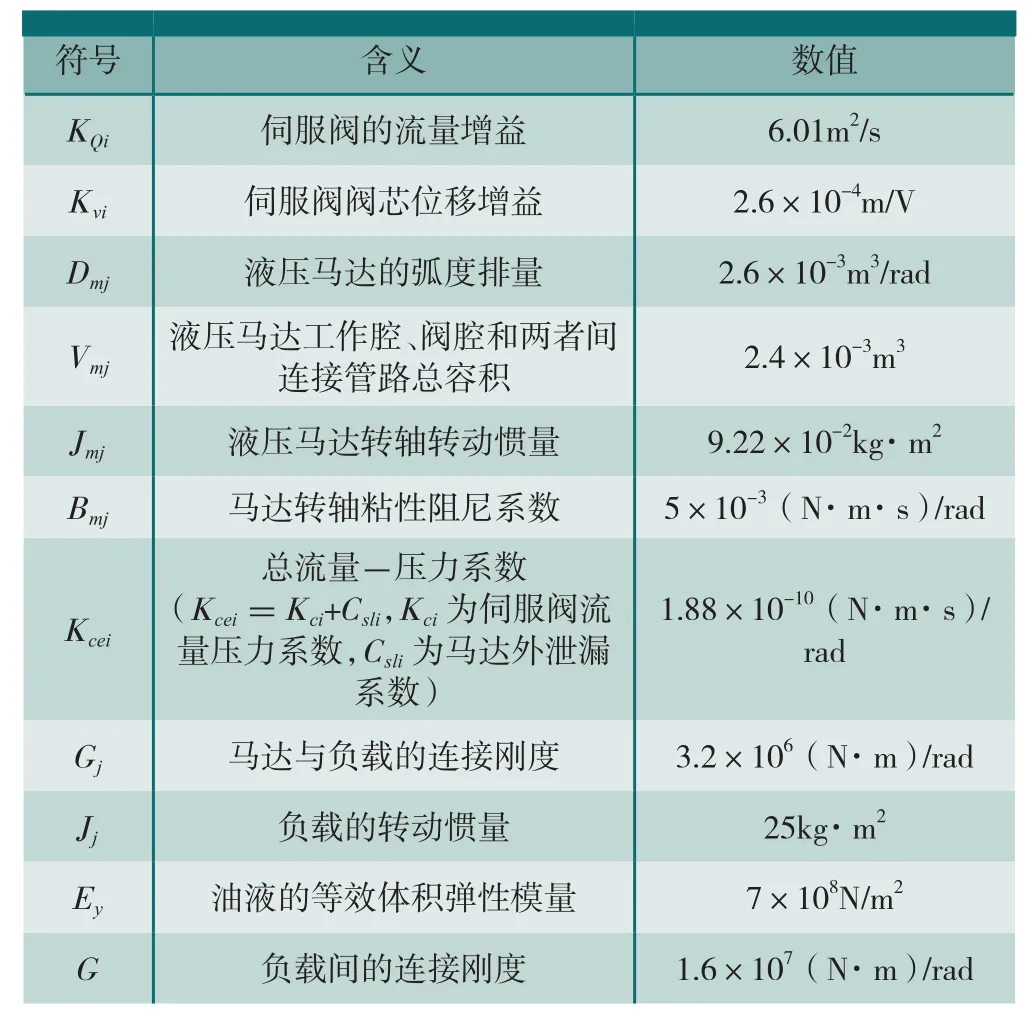
表1 双马达同步控制系统参数名义值

由式(1)、(2)得双马达同步系统方框图，如图2所示。

2 同步控制律设计

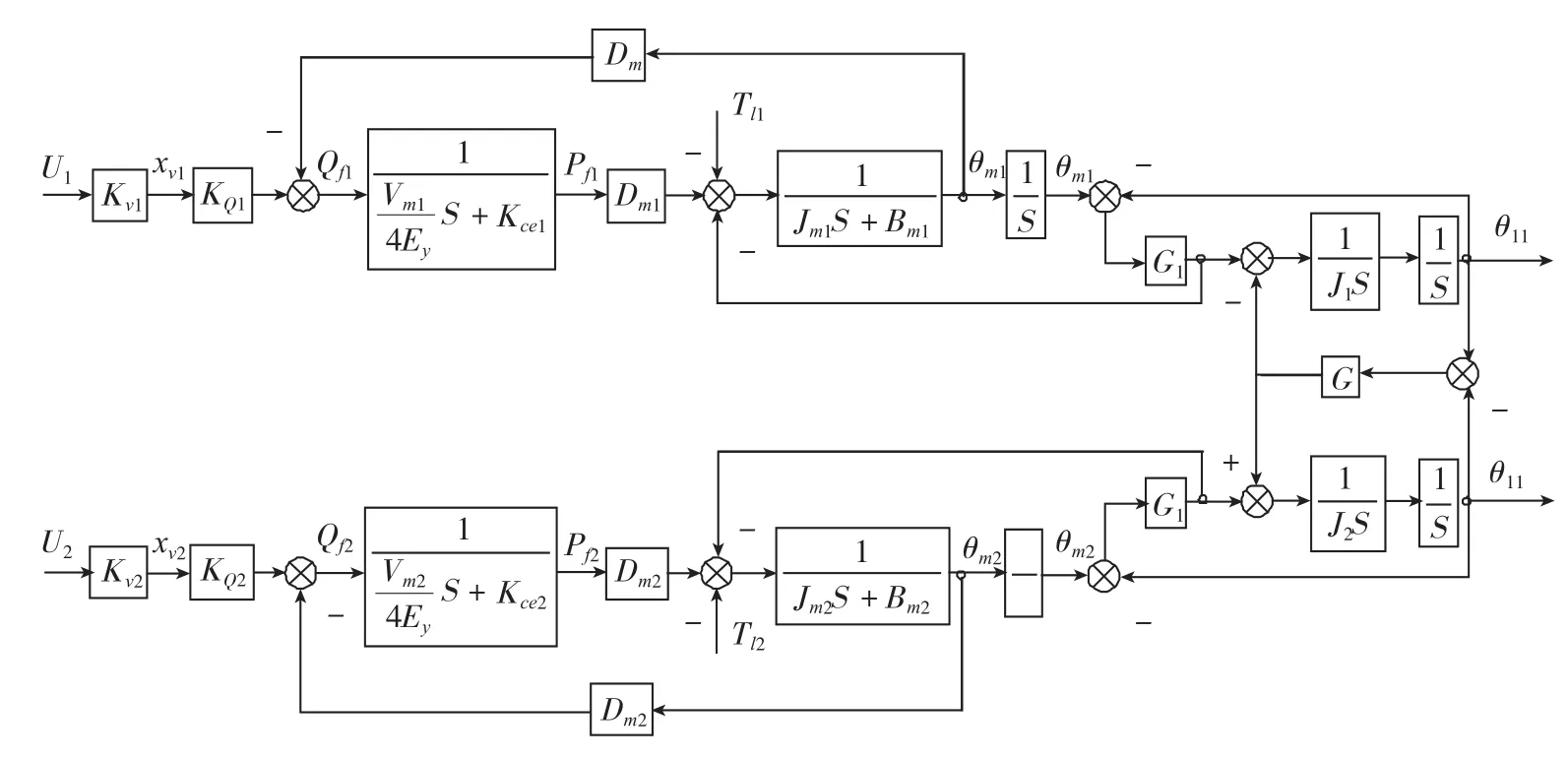
图2 双马达同步控制系统方框图Fig.2 Block diagram of DMSC

同步控制方案的设计目的是为了消除两个马达运动状态(位移、速度、加速度)或输出力的差异，即使θ1=θ2。对于负载为中空液压马达的同步系统，还有一个重要设计目标是使中空液压马达的变形最小[6]。基于这样的设计目标，选择马达运动状态差值和负载变形作为反馈，采用双马达同步精度、同步误差校正的控制方案。该方案在理论上是合理的，但在工程实践上，测量马达运动状态差值和负载变形量却不太实际。

另外，考虑到双马达同步系统两个通道不对称特性主要来自阀控马达的内泄漏，因此，采取如下同步控制策略：

(1)以马达压差差值为同步信号补偿两个通道泄漏特性的不对称；

(2)以马达1角位移信号为主反馈信号，采用PID控制改善同步系统的品质。硬件配置如图3所示。

图3 实际配置的双马达同步控制系统Fig.3 Actual configuration of DMSC

马达1和马达2的控制信号为：

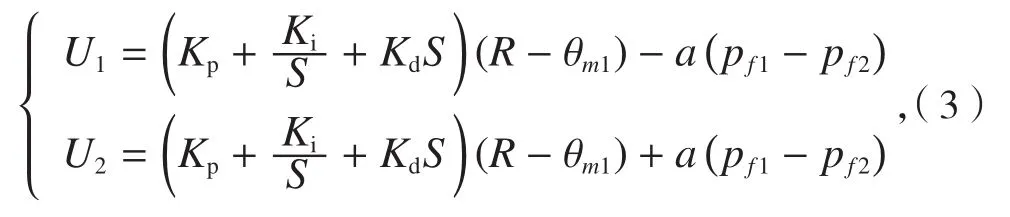
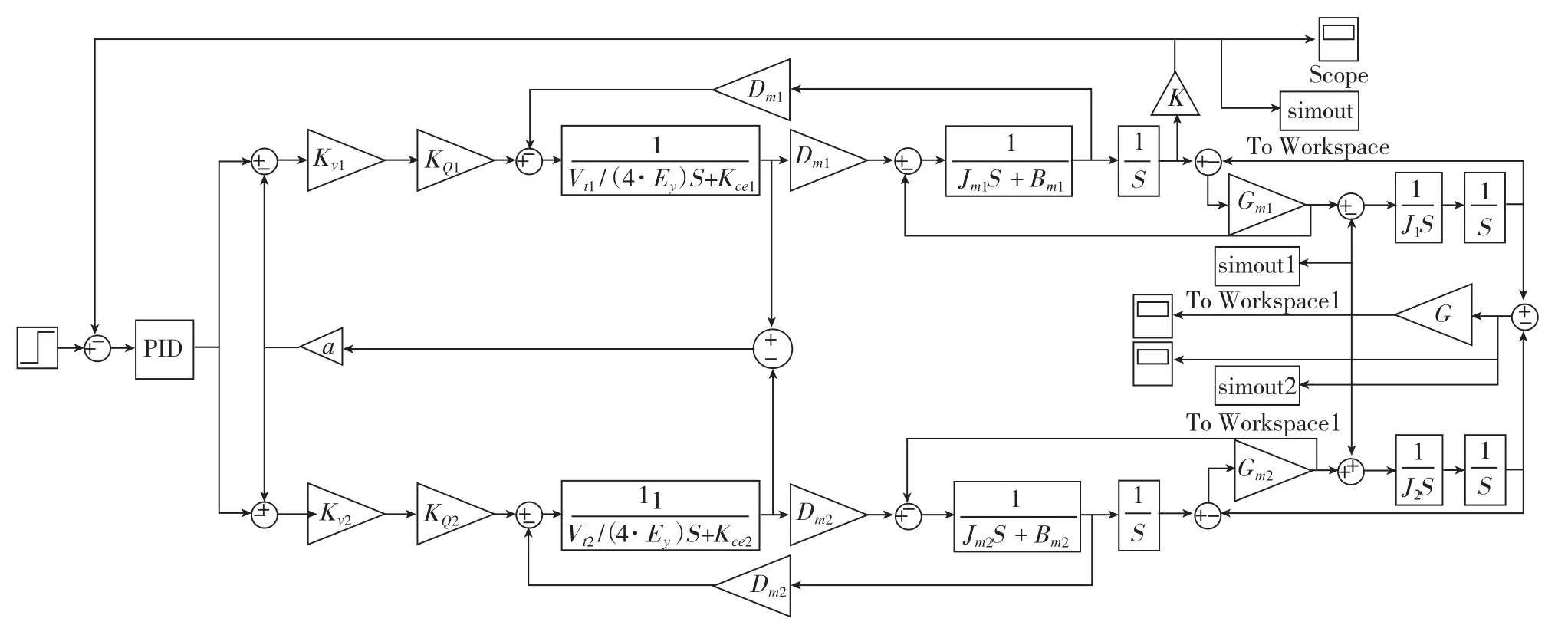
图4 双马达同步控制系统Matlab仿真方框图Fig.4 Block diagram of matlab simulation of DMSC

式中，R为指令信号；Kp、Ki、Kd分别为比例、积分、微分系数；a为马达压差差值反馈系数。

3 仿真分析

为了评价PID＋压差均衡控制策略对系统品质与负载变形指标的影响，通过系统阶跃响应曲线进行数值仿真。Matlab仿真框图如图4所示。

图4为空载工况下列车主被动头车的脱轨系数。曲线轨道上，刚性轮和弹性轮的脱轨系数均超过了限值，其中刚性轮的脱轨系数最大值为4.79，超过限值1.0的最大作用时间为23 ms，而弹性轮的脱轨系数最大值为2.69，超过限值1.0的最大作用时间为17 ms。相比于刚性轮，弹性轮的脱轨系数最大值降低了43.84%，超过限值的最大作用时间降低了26.09%。直线轨道上，刚性轮和弹性轮的脱轨系数都没有超过限值，弹性轮的脱轨系数最大值为0.31，略小于刚性轮的0.34。

PID 参数Kp=4、Ki=0、Kd=0.01，根据图4模型分别对下列几种情况做数值仿真。

(1)参数不对称的影响。取压差均衡参数a=0，令KQ2、Kce2、G2、J2分别为名义值的 80%、90%和 100%，按同等幅度变化，可得出结论：KQ2的变化对系统快速性和负载变形的影响最为明显；其次是G2和J2，Kce2的影响最弱。

(2)压差均衡对负载变形的影响。取KQ2、Kce2、G2、J2为名义值的90%，分别令压差均衡参数a为0和1×10-5进行仿真，可得出结论：系统作阶跃响应时，压差均衡参数a对KQ2、Kce2、G2引起的负载变形有明显的抑制作用，其中对KQ2引起的负载变形抑制最为明显；对J2引起的负载变形，压差均衡参数a使得最大负载变形略有增大，但收敛速度加快。

(3)PID对负载变形的影响及压差均衡对快速性的影响。取定PID参数Ki=0、Kd=0.01，KQ2为名义值的90%，压差均衡参数a为1×10-5，令Kp等于2和4进行仿真，可得出结论：利用PID参数的比例系数改善系统快速性，将使负载变形加剧，即系统整体性能与负载变形之间存在矛盾。

取定 PID 参数Kp=4、Ki=0、Kd=0.01，KQ2为名义值的 90%，令压差均衡参数 a分别为 0、1×10-5、1×10-4进行仿真，可得出结论：压差均衡参数a对系统快速性有细微的改善作用，但可以明显地抑制负载的变形。

仿真结果表明：

(1)通道主要参数不对称，将使负载产生变形；各参数中，伺服阀流量增益失配对负载变形的影响最大；相比较而言，与伺服阀流量-增益及马达泄漏系数相关的阀控马达系统的总压力流量系数的失配对负载变形影响比较小；

(2)压差均衡参数 a对KQ2、Kce2、G2引起的负载变形有明显的抑制作用，但会加剧J2引起的负载变形，因此双马达同步系统负载惯量应尽可能对称；

(3)压差均衡控制策略对系统快速性有微弱的改善作用，但对抑制主要参数失配引起的负载变形作用明显；PID控制策略中比例系统对系统快速性有改善作用，但会加剧主要参数失配引起的负载变形。

4 试验应用

双马达同步驱动的精度最终体现在三轴飞行转台系统的低速性能和频率响应、最大速度、最大加速度等动态指标上。将双马达同步驱动控制技术应用于某三轴液压转台上，并进行试验验证。

试验条件为油源压力9.5MPa，油温30℃，恒压泵的额定流量为400L/min，角位移传感器采用海德汉RON786增量式编码器，模拟负载转动惯量74kg·m2，偏心转距735N·m，重量484kg。

两通道同时输入幅值1°、频率为6Hz的正弦信号，系统的频率响应满足双十指标要求，如图5所示；系统0.001°/s的低速响应曲线比较平滑。输入幅值为20°的阶跃信号，对输出位置曲线分别进行一次和二次求导，得到最大速度和最大加速度响应曲线，最大响应速度达到 300°/s，最大加速度达到 35000°/s2，静态、动态性能都满足技术指标要求。图6为双马达同步驱动控制在某三轴液压转台上的成功应用。

图5 双十指标(6Hz)曲线Fig.5 6Hz curve

图6 双马达同步驱动控制在某三轴液压转台上的应用Fig.6 Application of DMSC on three-axis hydraulic motion simulator

[1] 徐东东，万红坡，孙志朋，等.基于LabVIEW的液压泵站远程监控系统设计与实现.液压气动与密封，2011(8)：41-43.

[2] 李尚义，赵克定，吴盛林.三轴飞行仿真转台总体设计及其关键技术 .宇航学报，1995，16(2)：63-66.

[3] 李军伟，赵克定.液压仿真转台中框等同式同步控制系统的研究 .液压与气动，2004(12)：31-32.

[4] 于双，王旭永，陶建峰.三轴转台中框双马达驱动控制技术研究 .液压与气动，2006(8)：46-49.

[5] 陶建峰，王旭永，刘成良，等.负载变形敏感双马达同步驱动系统建模与仿真.系统仿真学报，2007，19(7)：1574-1578.

[6] 陶建峰.电液伺服转台及其关键技术研究[D].上海：上海交通大学，2008.