机械传动空回对伺服性能的影响分析

陶 忠，鲁亚飞，贠平平，庞 澜，杨远成

（1.西安应用光学研究所，陕西 西安710065；2.国防科技大学 机电工程与自动化学院，湖南 长沙410073）

引言

典型伺服系统由驱动电机、传动机构、执行机构、传感器以及控制系统等组成，而传动机构作为伺服系统的重要组成部分，它的性能的好坏，直接关系到整个伺服系统工作品质的高低［1－3］。

新一代精密指向机构高精度、高动态特性等技术特点对机械传动机构提出了高刚度、无空回、高精度、小惯量的特性需求，而典型齿轮传动、带传动以及链传动等存在的固有空回、摩擦等非线性因素制约了精密指向机构伺服性能的提高［4－7］。

1 传动空回模型

传动空回又称为传动回程误差，主要由传动系统间隙、传动链弹性变形以及机械构件受载变形等因素组成［8］。

随着控制要求不断提高和空回非线性研究逐步深入，空回非线性模型也经历了不断地出新和完善。描述空回非线性的模型主要以迟滞模型、死区模型及“振－冲”模型最为广泛［9］。

假设动力传递过程中2个机械部件的传动示意图如图1所示，图中θm为驱动端输出转角，θL为从动端输出转角，K为刚性系数，c为阻尼系数，2j为传动空回，i为传动比，τ为系统传递转矩。

图1 机械传动部件传动空回示意图Fig.1 Schematic diagram of transmission backlash of mechanical transmission assembly

1.1 空回迟滞模型

空回非线性的迟滞模型可表示如下：

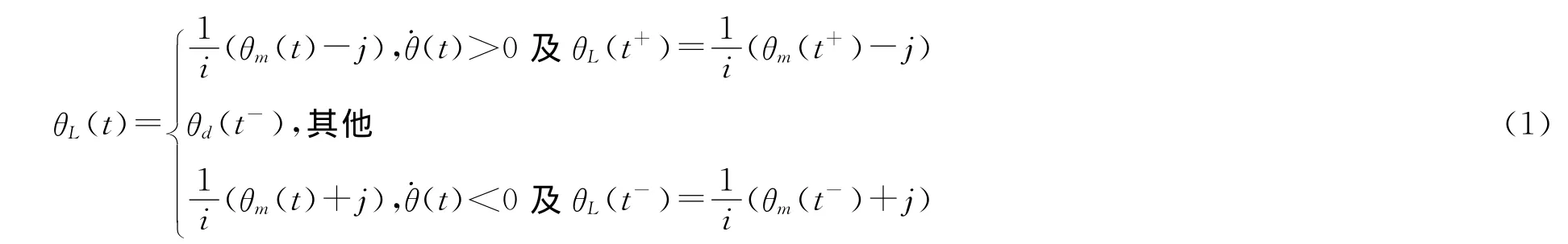
式中，t－、t＋分别表示控制过程发生的前后时刻。

空回非线性迟滞模型假设系统驱动部分在空回期间从动部件输出恒定，即从动部件由于存在大阻尼而在齿隙期间静止不动，或者由于驱动部分的转动惯量及阻尼比较小，在控制信号作用下可以很快跃过齿隙与从动部分接触。

1.2 空回死区模型

空回非线性的死区模型广泛应用于描述控制系统中的齿隙非线性。其模型描述如下：

式中z＝θm（t）－iθL（t）。

死区非线性模型通过系统驱动与从动部分的传递力矩来描述齿隙，它包含了系统刚性和阻尼的影响。对比发现迟滞模型的输入是位置，反映了输入与输出的位移关系，没有考虑阻尼，且假设传动是纯刚性的，而死区模型的输入是相对位置，输出是力矩，反映了系统驱动和从动部分的力矩传递关系，同时考虑了系统刚性及阻尼的影响。实际系统中，空回非线性只与输入和输出的相对位置有关，因而死区模型更符合实际情况。

1.3 基于Sigmoid函数的近似死区函数

由于迟滞模型和死区模型是不可微的，使得控制器的设计变得比较复杂，因此提出了一个连续的微分方程建立空回模型。

传统的死区近似函数如图2（a）所示，它的数学表达式如（3）式［10－11］：

图2 机械传动部件传动死区模型Fig.2 Transmission dead zone model of mechanical transmission assembly

为了替换上式中的分段连续不可微函数，采用一个连续可微函数来近似表示死区函数，如图2（b）所示。其由线性部分L＝z和非线性部分D＝η（z）两部分组成，表达式如下：

代入理想空回死区模型，得到连续的近似空回死区模型如下：

式中z＝θm－iθL。

（5）式即连续的近似死区模型，它反映了系统中驱动和从动部分的力矩传递关系，它的输入是相对位移z，输出是力矩τ，采用该可微模型虽然引入了有界误差，但由于误差较小，且克服了传统死区模型不可微的硬特性，方便了控制器的设计，并能改善系统的控制性能，增强使用性。

2 基于可微近似空回模型的机电伺服系统建模

针对典型的机电位置伺服系统，假设电机通过传动比为i的减速器驱动负载以指定的速度转动到目标位置。

设θm，θL分别为主、从动轮轴的转角、、Jm、JL、bm、bL分别为主、从动轮轴的角加速度、角速度、转动惯量和粘性摩擦系数，c和k为主从动轮结合部的阻尼系数和刚性系数，Ma为系统的输入转矩，τ为主从动轮接触时的传递力矩，空回为2j，则该伺服系统的动力学方程为

式中，Kd是电机扭转常数。

采用近似齿隙死区模型，则（6）式中τ（t）可表示成：

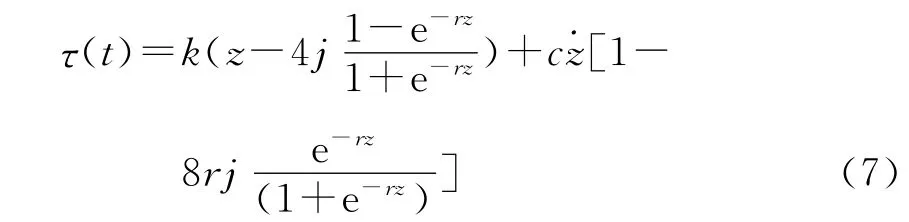
式中z＝θm－iθL。

令

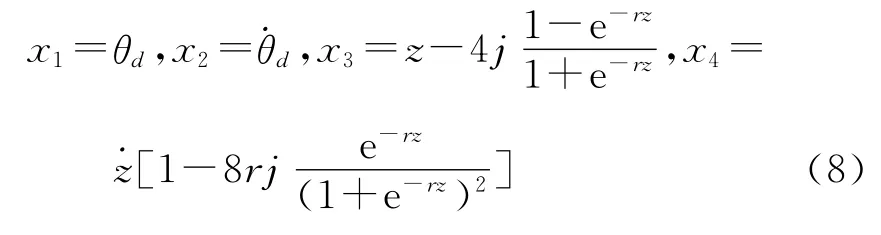
则τ（t）＝kx3＋cx4，它表示受空回非线性影响的传递力矩。系统的状态方程可写为

利用该伺服系统的状态空间方程，即可分析空回特性对系统伺服特性的影响。图3即考虑传动空回影响的伺服系统控制框图。

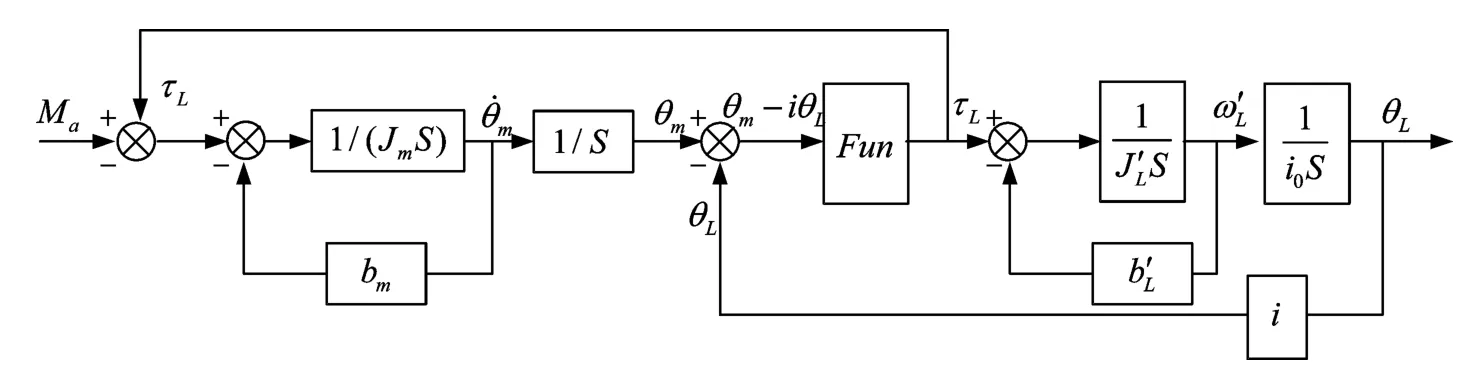
图3 考虑传动空回的机电伺服系统控制框图Fig.3 Control block diagram of considering transmission backlash of mechatronic servo system

图3中Fun即近似齿隙死区模型，它以相对角位移z＝θm－iθL为输入，传递负载转矩τL。基于考虑传动空回的机电伺服系统控制框图，可以对传动空回对伺服性能的影响进行进一步的分析。

3 传动空回对伺服性能影响的仿真实例

为了更加直观地分析传动空回对伺服性能的影响，基于可微近似空回模型在Matlab／Simulink环境下对传动空回对某典型伺服回路的特性进行仿真，Simulink模型如图4所示，仿真参数如下：

图4 基于可微近似空回模型的机电伺服系统Simulink仿真模型Fig.4 Simulink simulation model of mechatronic servo system based on approximation differentiable backlash model

1）传动空回对系统稳定性能的影响

在传动链的输入端输入一个幅值为1°的正弦信号φm＝sin（ωt）时，由于传动空回的存在，其输出波形为截顶的正弦波，并产生一个β角的相位滞后，如图5所示。2个图通过不同形式表征传动空回存在系统稳定性的影响，右边图为输入转角和输出转角随时间的变化，可以直观表现产生的相位滞后，左边图表征这个过程中输入转角和输出转角的关系，可以直观表征滞回曲线。这种滞后随着输入信号幅值的减小而增大。在输入信号较小时，甚至可以造成90°的相位滞后，造成系统不稳定。

图5 传动空回引起的伺服系统相位滞后Fig.5 Lag phase of servo system caused by transmission backlash

2）传动空回对系统控制精度的影响

对图4中基于可微近似空回模型的机电伺服系统Simulink仿真模型，在位置闭环情况下，施加幅值为1°，频率为0.2Hz的方波激励信号，同时测出负载端的角位置响应信号，如图6所示。由图6可以发现，伺服系统出现明显的极限环振荡。振荡过程是一个动态过程，造成了自振静态误差。

传动空回引起极限环振荡产生自振静态误差的物理过程：在伺服系统实现特定位置调转θm的过程中，由于空回的存在，起始状态下，电机需要转动一个空回的相应角度，而在空回范围内，电机轴上的负载几乎为零，电机带动传动链的输入轮会以很大的加速度撞击传动链的输出轮，而后带动负载运动，冲击的作用会使得负载以较大的速度冲过预定角度θm，形成反极性的误差电压，使得电机反转。而在反转过程中，由于空回的存在，电机仍以极大的速度和加速度转过空回的相应角度后才重新拖动负载反转，如此反复，就产生了极限环振荡。这种振荡不完全是由于负载的惯性作用产生，还附加了在空回范围内所积累的动能作用，因此，即使有足够的阻尼，也不能阻止由空回引起的系统的持续振荡。

图6 传动空回引起机电伺服系统自振静态误差Fig.6 Vibration and static error of electromechanical servo system caused by transmission backlash

4 结论

作为伺服系统中的重要组成部分，传动系统的刚度、传动误差、空回、摩擦等因素对伺服系统的静动态特性产生较大的影响。处在控制闭环内的传动空回对伺服系统的影响主要表现在2个方面：一是引起相位滞后，影响系统的稳定性；二是引起极限环振荡产生自振静态误差。

改善或消除传动系统非线性对伺服控制性能的影响途径可以分为2个方面：

1）通过控制手段，采用自适应补偿或者提高控制器增益等方法提高伺服系统的控制精度。然而，由于传动系统特性带来的固有非线性误差，采用控制方法往往难以有效地提升伺服性能，且在一定程度上增加了系统的复杂性和设计成本。

2）研究新型传动方式，从原理上降低或者消除传动系统固有的空回、摩擦等非线性因素。该方法从传动系统本身着手，可以从根本上消除传动因素对伺服控制性能的影响。

［1］ Zhang Lisong，Hu Youde，Xu Lixin.Principle and design of the servo system［M］.Beijing：Beijing Institute of Technology press，2008.张莉松，胡祐德，徐立新.伺服系统原理与设计［M］.北京：北京理工大学出版社，2008.

［2］ Zhang Jianwei，Zhang Lijun.Mechanical transmis－sion components affecting the performance factor of servo mechanism［J］.Mechanical Design and Manufacture，2001（1）：76张建伟，张莉军.机械传动部件影响伺服机构性能的因素［J］.机械设计与制造，2001（1）：76.

［3］ Baek J H，Kwak Y K，Kim S H.On the frequency bandwidth change of a servo system with a gear reducer due to backlash and motor input voltage［J］.Archive of Applied Mechanics，2003，73（5）：367－376.

［4］ Gutierrez H L.Performance assessment and enhancement of precision controlled structures during conceptual design［D］.USA：Massachusetts Institute of Technology，1993.

［5］ Townsend W T.The effect of transmission design on force－controlled manipulator performance［R］.USA：Dept.of Mechanical Engineering，Massachusetts Institute of Technology，1988.

［6］ Ma Yanling.Control and compensation of servo systems with backlash［D］.Xi'an：Xidian University，2008.马艳玲.含齿隙环节伺服系统的补偿控制［D］.西安：西安电子科技大学，2008.

［7］ Wu Yujing，Ji Ming.Compensation technology for high velocity tracking of electro－optical pod［J］.Journal of Applied Optics，2006，27（4）：293－297.吴玉敬，纪明.光电吊舱大速率平稳跟踪补偿技术研究［J］.应用光学，2006，27（4）：293－297.

［8］ Yang Qian，Shi Zhongxiu，Cheng Qiang.Research on dynamic simulation of linkage mechanisms with clearances based on Simulink［J］.Journal of Qingdao University：E ＆ T，2005，20（3）：16－21.杨倩，师忠秀，程强.基于Simulink的含间隙机构动力学仿真研究［J］.青岛大学学报：工程技术版，2005，20（3）：16－21.

［9］ Zhao Jianzhou，He Chao，Zhang Yuhe.An experimental study of compensation algorithms for backlash nonlinearity of servo systems［J］.Journal of Beijing Institute of Technology，2000，20（3）：317－321.赵建周，何超，张宇河.伺服系统间隙非线性补偿算法的研究［J］.北京理工大学学报，2000，20（3）：317－321.

［10］Liu Weiming.Influence of backlash on the natural frequency of the antenna system structure［J］.Radio Engineering，1998，28（4）：5－9.刘维明.间隙对天线结构系统固有频率的影响［J］.无线电工程，1998，28（4）：5－9.

［11］Cao Haizhou.PID control based on neural network of backlash nonlinear study［D］.Xi'an：Xidian University，2009.曹海舟.基于神经网络PID控制的齿隙非线性研究［D］.西安：西安电子科技大学，2009.