一种改进的模糊C-均值聚类算法*

郭华峰，洪年松，范渊

（浙江工贸职业技术学院 信息传媒学院，浙江 温州 325003)

0 引言

自从Jiulun Fan提出抑制式模糊C-均值聚类（简称S-FCM）算法以来[1]，其抑制式的思想就得到了广泛和深入的研究[2-4]，范九伦在综述文献[5]中较为详细的阐述了这一点。在众多研究文献中，文献[6]引入抑制门限，提出了半抑制式模糊C-均值聚类算法（简称HSFCM），改善了S-FCM算法的聚类效果。然而，该算法由于多添加了一个抑制门限的参数，所以其可操作性变得较差。针对这个问题，我们引入面向隶属度修正的模糊聚类参数选择方法，提出了改进的半抑制式模糊C-均值聚类算法。仿真实验表明，改进后的算法具有较好的可操作性，其参数选择方法具有较好的自适应效果，对于低维数据集和高维数据集都是有效的。

1 半抑制式模糊C-均值聚类算法

2003年，针对模糊C-均值聚类算法收敛速度慢的问题，Jiulun Fan引入抑制因子α（0≤α≤1），提出了抑制式模糊C-均值聚类算法。其算法步骤如下：

Step 1取模糊度1＜m＜∞，分类数2≤c≤n，迭代终止门限ε＞0，迭代次数l=0，抑制因子0≤α≤1，给定聚类中心点的起始值Z(0)。

Step 2根据(1)式计算隶属值 μij。

Step 3使用以下方法更新 μij，i=1,...,n，j=1,...,c： 如 果 μis=max1≤j≤cμij， 那 么 μis=1-α+αμis，

S-FCM算法由于对除最大隶属度之外的其它隶属度进行了抑制，加快了最大隶属度的增长，从而提高了算法的收敛速度。然而S-FCM算法具有聚类效果不佳的缺点，文献[6]引入了抑制门限β（0≤β≤1），提出了半抑制式模糊C-均值聚类算法。该算法步骤如下：

Step 1取模糊度1＜m＜∞，分类数2≤c≤n，迭代终止门限ε＞0，迭代次数l=0，抑制因子0≤α≤1，抑制门限β（0≤β≤1），给定聚类中心点的起始值Z(0)。

Step 2根据(1)式计算隶属值 μij。

Step 3使用以下方法更新 μij，i=1,...,n，j=1,...,c： 若 μis=max1≤j≤cμij， 如 果 μis＞β ， 那 么μis=1-α+αμis， μis'=αμis'（s'≠s），否则不作更新。

Step 4根据(2)式计算中心点Z(k+1)。

相比较S-FCM算法，HSFCM算法在Step3中对隶属度的抑制更新添加了一个条件，只有最大隶属度大于抑制门限，才进行抑制操作，这样就阻止了过小最大隶属度的不合理增长，改善了聚类的效果。然而，HSFCM算法由于在抑制因子参数的基础上又加入了抑制门限参数，使得在算法的初始化阶段step1需要设定两个参数的值，这降低了算法的可操作性。此时，如何提高HSFCM算法的可操作性就成了必须探讨的问题。

2 半抑制式模糊C-均值聚类算法的改进

相对于S-FCM算法，HSFCM算法难以操作是因为有抑制因子α和抑制门限β两个参数的值需要确定，所以可以从降低待选择的参数个数方面着手。借鉴文献[7]面向隶属度修正类模糊聚类算法提出的参数选择方法，对抑制因子α进行参数选择，我们得到了α的自适应取值公式：

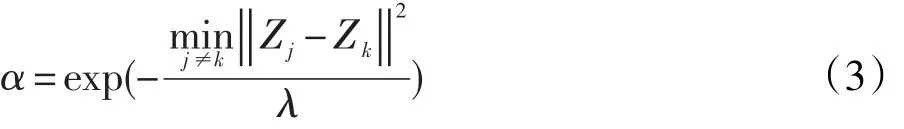
Step 1取模糊度1＜m＜∞，分类数2≤c≤n，迭代终止门限ε＞0，迭代次数l=0，抑制门限β（0≤β≤1），给定聚类中心点的起始值Z(0)。

Step 2根据(1)式计算隶属值 μij，根据(3)式计算抑制因子α。

Step 3使用以下方法更新 μij，i=1,...,n，j=1,...,c： 若 μis=max1≤j≤cμij， 如 果 μis＞β ， 那 么μis=1-α+αμis， μis'=αμis'（s'≠s），否则不作更新。

Step 4根据(2)式计算中心点Z(k+1)。

观察算法步骤可知，相对于HSFCM算法，I-HSFCM算法不需要在算法初始化阶段设置抑制因子的值，只是在Step2中加入了对抑制因子的自适应计算，这减少了HSFCM的参数选择，提高了算法的可操作性。为了验证I-HSFCM算法的有效性，进行以下实验。

3 仿真实验

实验一，随机生成4堆正态分布的数据点，每堆50个数据，共200个数据点，如图1所示。

图1 随机生成的正态分布数据点

在图1所示的数据集中使用新提出的I-HSFCM算法和抑制因子α分别为0、0.2、0.4、0.6、0.8和1的HSFCM算法，取抑制门限β=0.5，同时设置各种算法的模糊度m=2，分类数c=4，其他的初始条件也设置相同，执行上述算法20次，取其平均，得到如表1所示的结果。

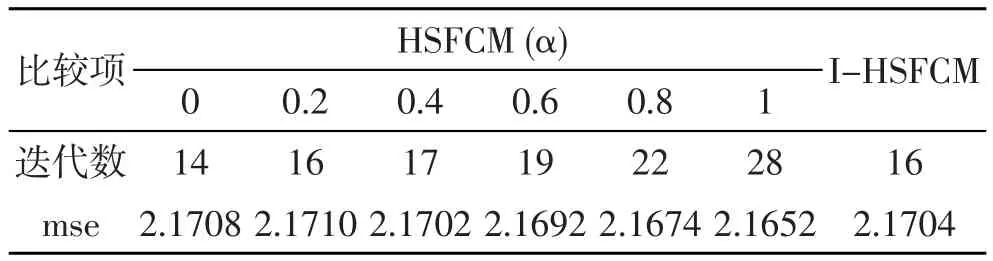
表1 I-HSFCM算法和HSFCM算法对图1数据的聚类结果

从表1可以发现，相对于不同抑制因子的HSFCM算法，I-HSFCM算法在迭代数和mse方面取得了较好的平衡，迭代数处于较少的水平，这表示收敛速度得到了较好的提升，同时mse也处于较小的水平，这说明收敛效果也得到了较好的维持。从表1的结果可以看出，I-HSFCM算法对于抑制因子的参数选择取得了较好的自适应效果。同时我们也得到了I-HSFCM算法在不同抑制门限β的情况下对图1数据的聚类结果，如表2所示。

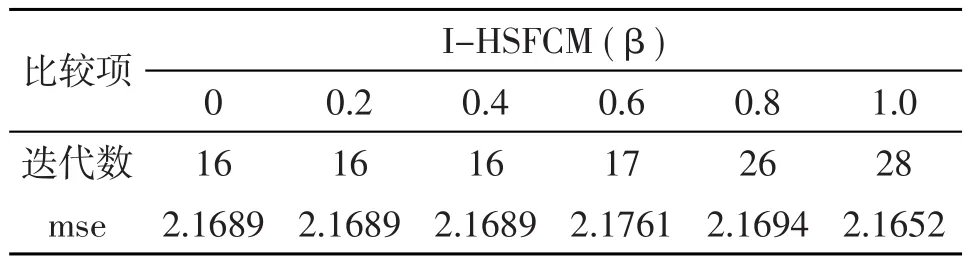
表2 不同抑制门限的I-HSFCM算法对图1数据的聚类结果

由于β=1时I-HSFCM算法等价于FCM算法，所以表2的数据表明，I-HSFCM算法对于抑制因子的自适应选择并没有降低收敛速度的提升，相对于FCM算法，I-HSFCM算法保持了S-FCM算法和HSFCM算法在收敛速度提升上的优势，且收敛效果不差，这说明I-HSFCM算法是有效的。以上是算法在二维数据集的表现，下面进行高维数据集的实验。

实验二，为了更好的检验I-HSFCM算法的性能，采用模糊聚类中经典的高维数据集Iris和Wine[8]。与实验一相同，使用I-HSFCM算法和抑制因子α分别为0、0.2、0.4、0.6、0.8和1的HSFCM算法，取抑制门限β=0.5，同时设置各种算法的模糊度m=2，分类数c=3，其他的初始条件也设置相同，执行上述算法20次，取其平均，得到如表3所示的结果。

表3 I-HSFCM算法和HSFCM算法对Iris、Wine数据集的聚类结果

表3的结果表明，在高维数据集中I-HSFCM算法也取得了收敛速度和聚类效果的平衡，其总体表现处于较优水平。另外我们也发现，在维数越高的Wine数据集中，I-HSFCM算法对于收敛速度的提升更明显。这说明I-HSFCM算法在高维数据集中也同样有效。

4 结论

针对HSFCM算法由于初始化参数过多而可操作性差的问题，引入面向隶属度修正模糊聚类的参数选择方法，得到了改进的I-HSFCM算法。I-HSFCM算法使用迭代公式对抑制因子进行自适应选择，减少了HSFCM算法的参数选择个数，提高了算法的可操作性。仿真实验表明，该算法在收敛速度和收敛效果方面取得了较好的平衡，对低维数据集和高维数据集，都具有较好的自适应效果，这说明算法的改进是有效的。

[1]Jiu-Lun Fan,Wen-Zhi Zhen,Wei-Xin Xie.Suppressed fuzzy c-means clustering algorithm[J].Pattern Recognition Letters,2003,24:1607-1612.

[2]F.Zhao,J.L.Fan,H.Liu.Optimal-selection-based suppressed fuzzy c-means clustering algorithm with self-tuning non local spatial information for image segmentation[J].Expert Systems with Applications,2014,41(9):4083-4093.

[3]W.L.Hung,D.H.Chen,M.S.Yang.Suppressed fuzzy-soft learning vector quantization for MRI segmentation[J].Artificial intelligence in medicine,2011,52(1):33-43.

[4]L.Szilágyi.Lessons to learn from a mistaken optimization[J].Pattern Recognition Letters,2014,36:29-35.

[5]范九伦.抑制式模糊C-均值聚类研究综述[J].西安邮电大学学报,2014,19(3):1-5.

[6]黄建军,谢维信.半抑制式模糊C-均值聚类算法[J].中国体视学与图像分析,2004,10(2):109-113.

[7]郭华峰,陈德华,陆慧娟.面向隶属度修正模糊聚类的参数选择方法[J].计算机系统应用,2015,24(1):166-170.

[8]C.L.Blake,C.J.Merz.UCI repository of machine learning databases.[http://archive.ics.uci.edu/ml/].Irvine,CA:University of California,Department of Information and Computer Science,1998.