随机子空间法在谐波电能计量中的应用

马 亮

（山东省电力公司安丘供电公司，山东 潍坊 262100）

电力系统中，由于电力电子设备的广泛应用，很容易对电网造成谐波污染[1]。谐波污染在一定程度上严重影响企业的安全生产以及居民用电安全，且在谐波情况下，很难保证电能计量的准确性。当负荷为线性负荷，电网存在多次谐波，电能表的计量是基波电能加上电网注入负荷的谐波电能，将会为用户造成经济损失；而当负荷为非线性负荷并向电网中注入谐波时，电能表的计量是基波电能减去注入电网的谐波电能，会对电网造成经济损失[2]。故而如何在电网中存在谐波的情况下实现准确计量显得尤为重要。

目前电能计量方法中应用较为广泛是基波电能和谐波电能分别计量，然后计算总和以得到总的电能消耗量。准确得到谐波电能是准确电能计量的前提，快速傅里叶变换（Fast Fourier Transform，FFT）[3-4]是比较成熟的谐波检测方法，但此方法一般只可得到谐波频率和幅值，对于谐波相位很难准确检测出。文献[5]提出利用小波来分析电能计量中的谐波问题，但小波存在基波选取困难的问题。

为了准确分析电网中的谐波，本文提出采用随机子空间法（Stochastic Subspace Identification，SSI）[6-7]来分析电能计量中的谐波问题，SSI 通过构造Hankle矩阵，进行奇异值分解（Singular Value Decomposition，SVD），通过SVD 可得到奇异值，根据奇异值的大小可确定系统模态阶数，使SSI 算法具有一定的抗噪能力，在实际电网中更能准确辨识出谐波参数。本文应用SSI 对谐波电流、电压信号进行分析，通过对谐波参数的准确辨识，以实现谐波电能的高精度计量。

1 基本原理

电力系统中的谐波信号可拟合为

式中，Ri为幅值，fi为频率，φi为初相。

1.1 随机子空间理论

SSI 的通过构造Hankle 矩阵，前i个采样点作为“过去”采样点形成一个矩阵，第i个采样点之后看做“将来”采样点形成另一个矩阵，“将来”的输出行空间投影到“过去”的输出行空间，投影结果是保留了“过去”的全部信息，并用此预测“将来”的信息。“将来”和“过去”的矩阵组成一个新的矩阵并乘以一个系数的形式。SSI 复杂度低，因为只运行一次SVD 分解，故而运算效率高。

对于白噪声激励的线性系统，随机状态空间模型可以表示为

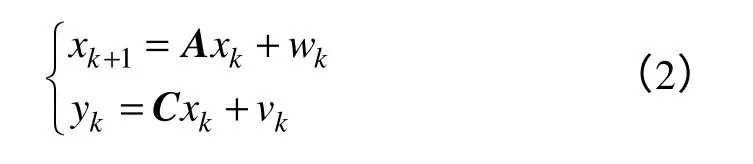
式中，yk∈Rl×l为第l个测点，在第k（k∈N）个采样间隔（Δt）的输出向量；xk∈Rn×l为系统的状态向量，n为系统的阶数；A∈Rn×n为系统矩阵；C∈Rl×n为输出矩阵；wk∈Rn×l为系统噪声污染；vk∈Rl×l为测量噪声；wk和vk互不相关。

根据系统输出yk构造Hankel 矩阵H

式中，Y0/2i-1的下标0/2i- 1表示Hankel 矩阵第一行块和最后一行块；下标p和f分别表示“过去”和“将来”。

定义输出yk自协方差矩阵Ri为

由协方差序列组成的Toeplize 矩阵T1/i为

对矩阵T1/i进行奇异值分解，秩为非零的奇异值个数，即为系统阶数。

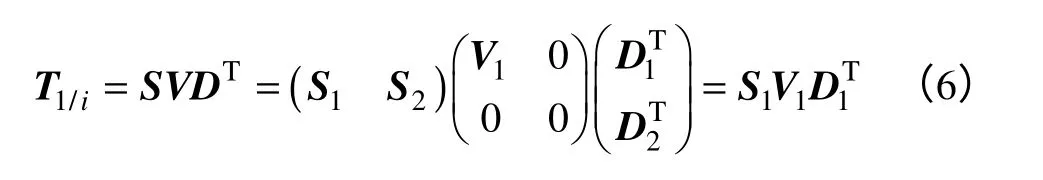
式中，S1∈Rli×n；V1∈Rn×n；D1∈Rli×n；n表示系 统阶数，阶数可用SVD 分解法确定。

T1/i可分解为

式中，Oi为可观矩阵；Γi为反转随机可控矩阵。

根据上式可得到系统矩阵A和C。

1.2 谐波参数辨识

对系统矩阵A做特征值分解

式中，Λ=diag [λ1,λ2,… ,λi,…,λn]∈Cn×n，λ i为系统特 征值；Ψ=[ψ1,ψ2,…,ψn]∈Cn×n为 系 统特征向 量矩阵；n表示系统阶次。

可通过式（10）计算出谐波的频率和衰减系数

式中，λic表示系统特征值，λic和λic*互为共轭，Δt表示采样时间间隔，fi为频率。

进而通过最小二乘得到各次谐波的幅值和相角对于N个采样数据存在

其中

式中，n表示得到的谐波个数。

则P的最小二乘解为

则各变量的幅值Ri和相角φi可求得为

由此已经求得各谐波量的幅值、频率、相角。

1.3 谐波功率计算

在电网中存在谐波的情况下，谐波电流和谐波电压分别表示为

式中，n表示谐波次数，Ij和Uj分别表示谐波电流和谐波电压的幅值，φi和φu分别表示谐波电流和谐波电压的相位。

谐波的有功功率可用瞬时功率来计算

同理，谐波的无功功率可表示为

由式（17）和式（18）即可计算得到相应的谐波电能。

1.4 谐波电能计量方案

通过SSI 方法准确的辨识出电网中的谐波电流和谐波电压参数后，进一步求出谐波功率，从而实现了谐波电能的准确测量。流程图如图1所示。

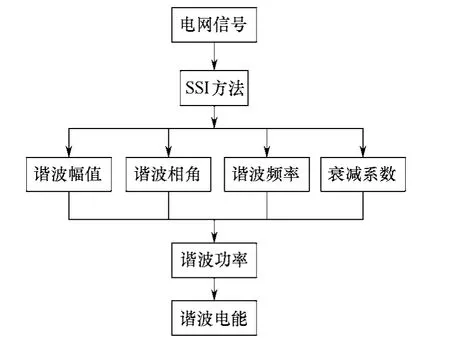
图1 SSI 辨识谐波流程图

2 仿真分析

2.1 理想信号分析

为了验证SSI 方法在谐波参数估计方面的有效性，构造如下理想信号进行分析。

其中

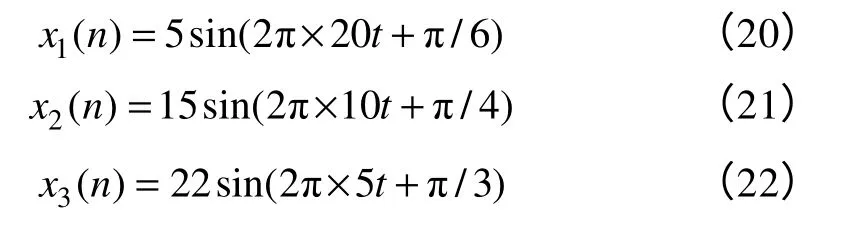
首先利用FFT 算法对式（19）所示的理想信号进行分析，分析结果如图2所示。

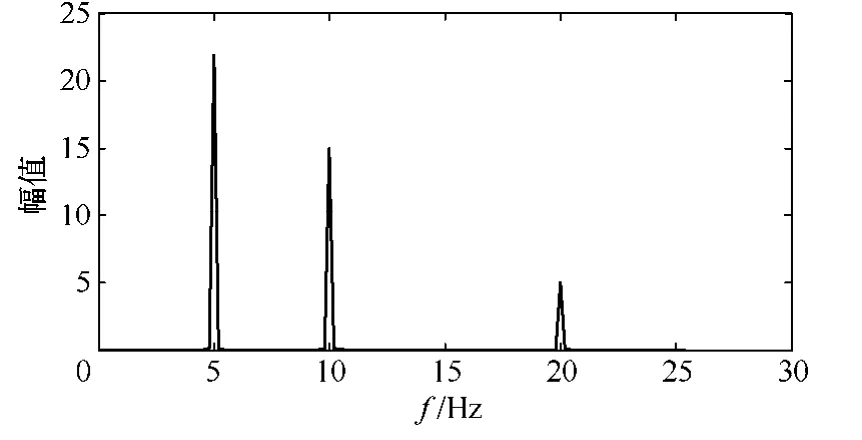
图2 FFT 分析结果

由图2可知，通过FFT 无法分析得出谐波的相位。FFT 的分析结果和SSI 的分析结果对比见表1。

由表1知，同FFT 方法相比，SSI 方法具有更高的辨识精度，且能获得相位信息，更能满足实际系统电网中电能计量的需要。

2.2 PSCAD 仿真算例

在PSCAD/EMTDC 仿真软件中搭建六脉动换流阀接理想电源的拓扑图，换流阀的主要构成为晶闸管电力电子设备，在实际运行当中会向电网输入6k±1 次特征谐波，其中k=0,1,2,…,n。本算例通过仿真得到谐波的时域仿真结果，并用SSI 算法对谐波电流进行检测。系统拓扑结构图如图3所示。

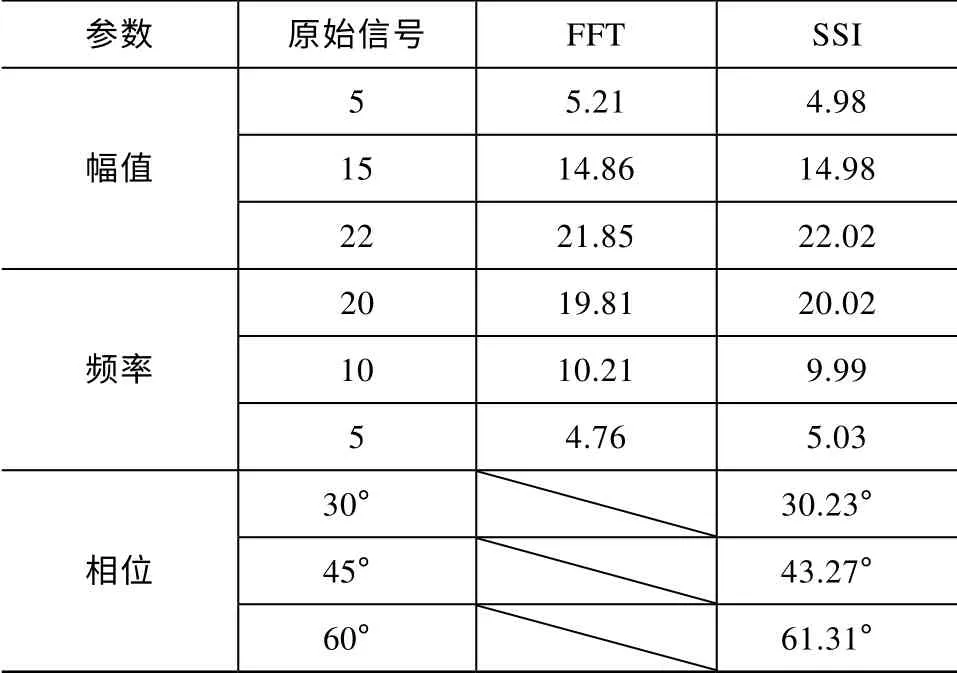
表1 FFT 和SSI 的对比结果

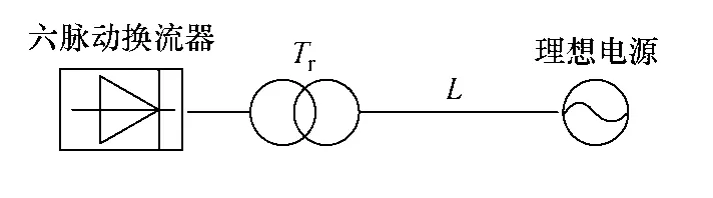
图3 仿真拓扑结构图

图3中，L为输电线路，理想电源的机端电压为0.2kV，六脉动换流器经过一个0.2kV/0.2kV 的变压器与理想电源相连，此变压器仅作为换流器与电源间的接连变压器使用，接线方式为输电线路电压有效值为200V，电流有效值为100A。系统基波频率为50Hz，信号采样频率为100000Hz。

经过PSCAD 时域仿真，得知换流器向电网注入5、7、11、13 次谐波。谐波电流仿真波形图如图4所示。

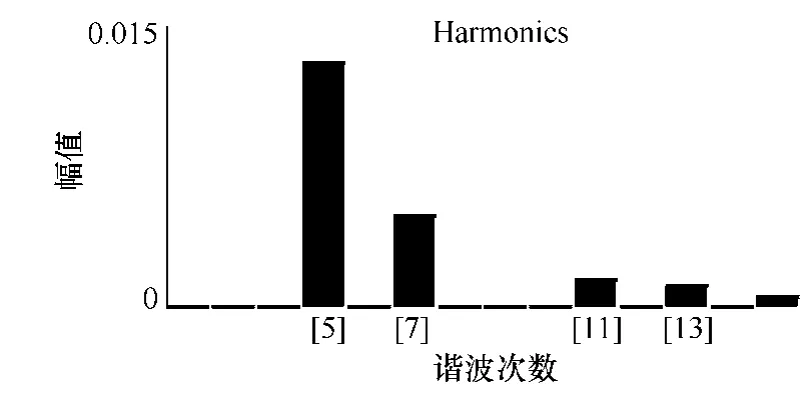
图4 谐波次数仿真图

取出线路中三相电流信号，如图5所示。

图5 线路电流时域仿真图

由图5可知，电流中存在谐波电流，严重影响基波电流。

采用SSI 算法对线路中的谐波电流进行辨识，辨识结果见表2。

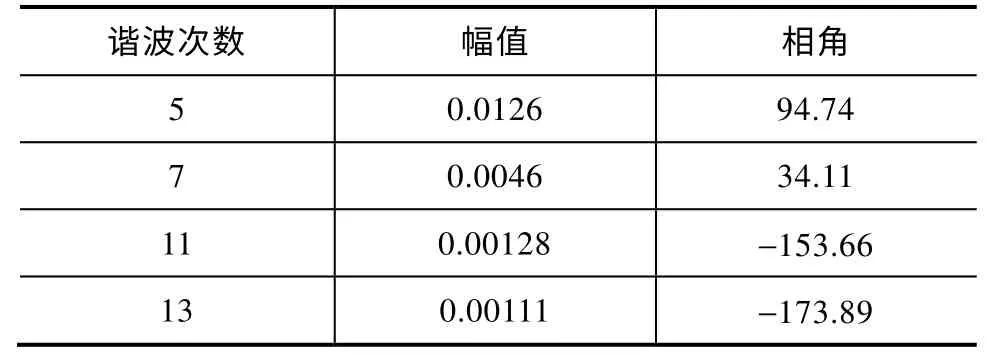
表2 谐波电流辨识结果

同理，谐波电压的辨识结果见表3。

表3 谐波电压辨识结果

故而可根据表2和表3的辨识结果计算出相应谐波次数的电能消耗，相应谐波次数的电能消耗见表4。

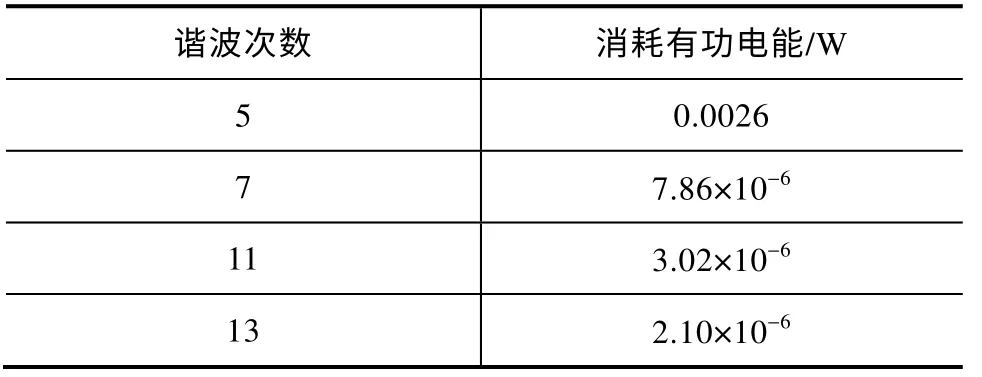
表4 谐波次数电能消耗

由表2至表5可知，通过SSI 准确辨识出线路中的谐波电流和谐波电压的幅值、相位后，即可通过式（18）、式（19）计算出谐波电流、电压消耗的功率。

3 结论

鉴于FFT 无法辨识出谐波量的相位，小波分析谐波时存在小波基波选取困难的问题，本文提出利用随机子空间法来分析电网中的谐波电流和谐波电压参量。

本文通过理想算例将SSI 与FFT 对比分析，验证了SSI 算法可准确辨识谐波参量，在得到准确的谐波参量前提下，进一步通过成熟的谐波功率计算方法得到较为准确的谐波功率。

在实际电网中，通过随机子空间法分析谐波电流和谐波电压的详细参量可计算出谐波消耗的电能，进一步提高了电能计量的准确度，保证了用户和电网的利益。

[1] (美) Francisco C.De La Rosa,赵琰,孙秋野译.电力系统谐波[M].北京: 机械工业出版社,2009.

[2] 刘座铭,吕项羽,常学飞,等.电力谐波对电能计量的影响及治理措施[J].吉林电力,2013,41(2): 32-34.

[3] 曹健,林涛,张蔓,等.电力系统间谐波检测方法[J].高电压技术,2008,34(8): 1745-1750.

[4] 庞浩,李东霞,俎云霄,等.应用FFT 进行电力系统谐波分析的改进算法[J].中国电机工程学报,2003,23(6): 50-54.

[5] 胡智宏,杜晓冉.小波分析在谐波电能计量中的应用[J].郑州轻工业学院学报（自然科学版）,2013,28(3): 79-82.

[6] 刘洋,田石柱.基于随机子空间的结构参数识别及振动台试验验证[J].地震工程与工程振动,2004,24(2) : 111-117.

[7] 徐良,江见鲸,过静珺.随机子空间识别在悬索桥实验模态分析中的应用[J].工程力学,2002,19(4): 46-49.