基于中心流形理论的风力发电系统 非线性控制策略研究

刘 军 段 韬

（西安理工大学自动化学院，西安 710048）

由于永磁同步风力发电系统具有机械损耗小、运行效率高、安全可靠、便于维护等优点，近年来，得到了广泛的运用。

永磁同步风力发电系统的最大风能跟踪通常采用PI 控制器，虽然PI 控制对系统内部参数的变化和外部干扰具有一定的适应能力，但是由于控制器参数是固定值，所以当外部干扰较大时，系统的性能会受到较大影响，甚至不稳定[1]。

在现代控制理论与应用中，线性系统占据非常重要的位置，其基本理论已发展得相当完善。但是实际的系统绝大多数都是非线性的，对外部扰动和参数变化也比较敏感，控制效果往往不理想。

近几十年来，以微分几何和微分对策为基础的非线性控制理论快速发展，其中非线性系统的零动态线性化设计方法，因其构思比较巧妙，往往能得到较好的设计效果[2]。

由于滑模变结构控制具有对干扰的不变性和降阶特性等特点，越来越受到人们的重视。在常规的反馈控制器上加上滑模变结构控制，可以提高系统的抗干扰能力。

因此，本文把两种方法相结合，运用于永磁同步风力发电机最大风能跟踪控制上，既可以减少系统对精确数学模型的依赖性，同时线性化也有助于建立线性滑模函数。

1 风力发电系统模型

1.1 风速模型

风力发电系统中，组合风速可以较好的反映自然风速的特性，尤其是在风速突变时，能够全面地检验风力发电系统的性能，乃至整个系统的抗干扰性[3]。

组合风速中，可将自然风速v分为基本风速vb、阵风vg、渐变风vr和噪声风vn。其数学模型为

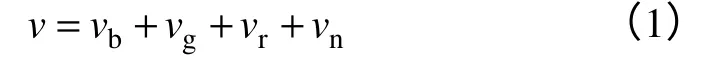
1.2 风力机模型

风力机是用来捕获空气动能并转换为机械能，其工作性能决定了整个风力发电系统的有效输出功率且直接影响到机组的安全稳定运行。

永磁同步风力发电机转子的运动方程为

式中，J为发电机转子和风力机的总转动惯性系数；Tωt为发电机输入的机械转矩；Tg为发电机输出的电磁转矩；ωg为电机转速。

风力机输入的机械转矩为

式中，ρ为空气密度；R为风轮半径；v为风速；Cp为风能利用系数；λ为叶尖速比；Cq为风机非线性转矩系数；β为桨距角。

文献[4-5]指出风机的非线性转矩系数Cq可以用叶尖速比λ的六次多项式拟合来表达。Tωt的六阶表达式比较复杂，计算量大，为了计算方便，忽略启动过程，可用一个二阶多项式近似代替。

二阶方程已经很好的描述了最佳工作状态附近λ的特征[6]。

发电机输出的电磁转矩为

式中，p为极对数；Φd、Φq为d、q 轴的磁通；Ld和Lq为定子d 轴和q 轴电感，同时Ld=Lq=L；id和iq为定子d 轴和q 轴电流；Φm为永磁同步电机磁通。

1.3 风力发电系统模型

在dq 同步旋转坐标系下，永磁同步发电机的模型如下

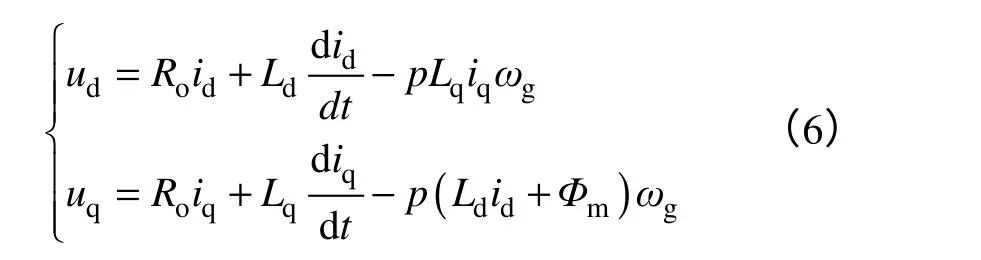
式中，Ro永磁同步电机定子电阻。

设永磁同步风力发电系统的简化结构如图1所示。

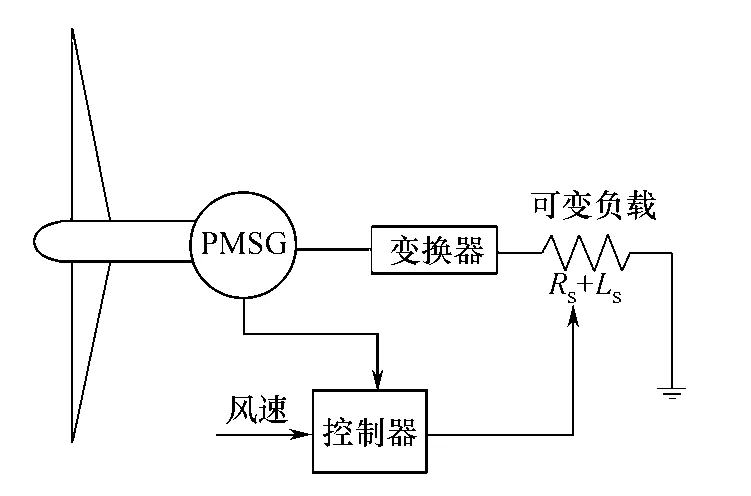
图1 永磁直驱风电系统等效模型

该控制系统的简化结构基于以下考虑[7-8]：

1）本文研究的重点在于最大风能跟踪控制，并且假设其他部分都正常工作。

2）风电系统的电气动态远远比机械动态快，根据奇异摄动系统理论[9]，各子系统的动态响应速度相差较大时，研究的“慢”动态子系统时，可以忽略“快”子系统的动态影响，认为其响应瞬间完成，其值始终处于“准稳态”。

3）风力发电系统的功率经过变流后，网侧相当于负载，故简化为等效阻抗Rs和Ls表示。

根据式（2）～式（6），直驱永磁风力发电系统的整体动态特性数学模型为

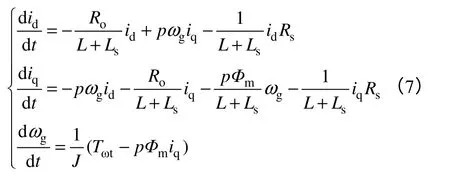
式中，Rs和Ls为等效阻抗，Rs为可变电阻，Ls为定电感。

2 系统的控制策略

2.1 PI 控制

风力发电系统的机侧控制主要有转速环PI 控制和功率环PI 控制，其具有设计简单和适应性好等特点，但永磁同步电机的强非线性使PI 参数难以整定，给实际运用带来了一定困难[10]。风力发电系统机侧转速和功率PI 控制系统结构图如图2和图3所示。 图中，G(s)发电机和变流器动态简化为的传递函数。

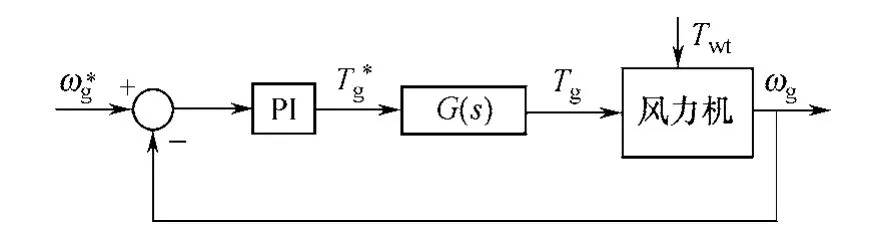
图2 转速PI 控制框图

图3 功率PI 控制框图

2.2 中心流形理论

如果S是一个光滑的子流形，且局部不变，S在x=0 的切空间恰为由A 的零实部特征值所对应的特征向量所张成，则称流形S是系统所在的中心流形。对中心流形定理介绍如下[11]：

考虑非线性系统（8）

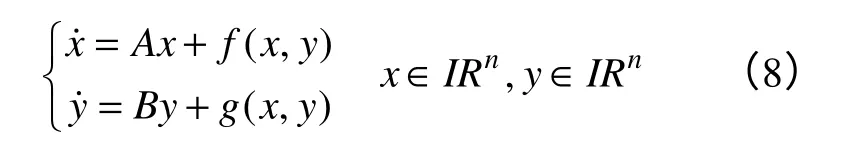
式中，f、g为充分光滑函数。

f(0,0)=0,g(0,0)=0,Dx(0,0)=0,Dfx(0,0)=0,Dfy(0,0)=0,Dgx(0,0)=0,Dgx(0,0)=0。A，B 分别为n×n,m×m矩阵，其的特征根分别有零实部和负实部，(0，0)是系统的一个平衡点。

定理1：如果f(x,y)和g(x,y)属于Ck（k次可导函数，k≥2），那么存在一个中心流形y=h(x)使之属于Ck-1。将中心流形y=h(x)带入式（8）中得到n维约化系统：

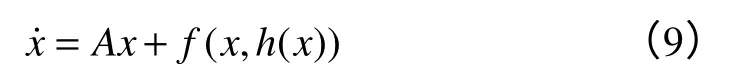
定理2：如果约化系统式（9）的平衡点是局部稳定（不稳定、渐进稳定）的，那么原系统式（8）的平衡点也是局部稳定（不稳定、渐进稳定）的。将式（8）代入式（9），得到h(x)，应满足方程

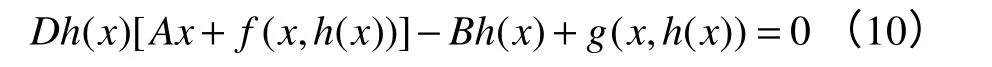
同时，h(0)=0,Dh(0)=0。

实际运用当中，h(x)不能由式（10）精确求解，但是通过定理3 能得到h(x)一定精度的近似解。

定理3：假设有C1函数φ：IRn→IRm，它满足φ(0)=0，Dφ(0)=0，且有某个常数p＞1，使得N(φ(x))=O(|x|p)在x→0 时，h(x)=φ(x)+O(|x|p)。

2.3 基于中心流形理论的零动态原理及其设计[12]

在非线性系统零点平衡状态问题上，中心流形理论可以为非线性系统在临界情况下进行稳定性设计。而实际工程中，传统的零动态设计方法难以使系统的输出量在任何时刻都保持在零值。所以为了克服传统零动态设计方法的缺点，采用中心流形理论并结合状态反馈线性化方法，设计新的零动态。

文献[13]在推导出永磁同步电动机数学模型的基础上，应用中心流形定理，得到了其简化的中心流形方程，并在此基础上讨论了其稳定性及其分支情形。

考虑系统（8），输入函数

y=h(x)相对于系统输入u的关系度r小于系统阶数n。通过坐标变换z=φ(x)和反馈v=a(ε,η)+b(ε,η)的作用，可以把系统(11)变换为

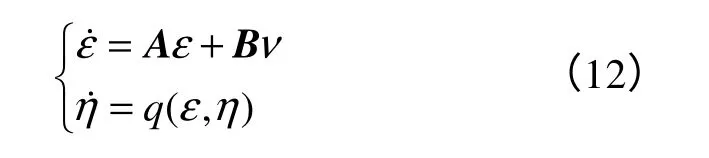
式中

同时，若零动态=q(0,η)在η=0 处渐进稳定，则在线性控制律u*中，线性系统=Aε+Bv可以在(ε，η)=(0，0)处镇定系统（11）。

选取状态变量x=[x1,x2,x3]T=[id,iq,ω]T，控制输入为u=Rs，输出为转速y=ωg，对式（4）化简

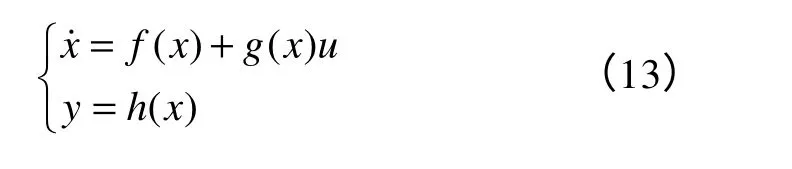
其中

对函数h(x)进行李导数递推运算，则有

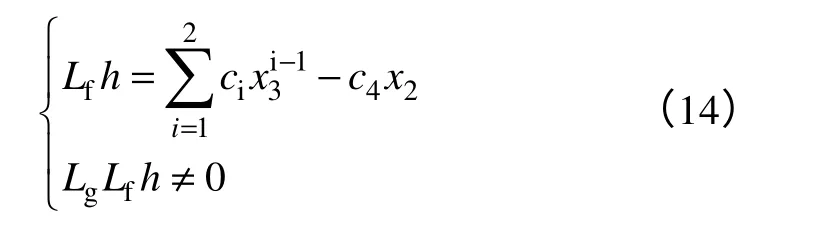
系统的相关度为2＜3，只能实现部分线性化，故采用零动态设计原理。

先进行Z坐标变换z=Φ(x)

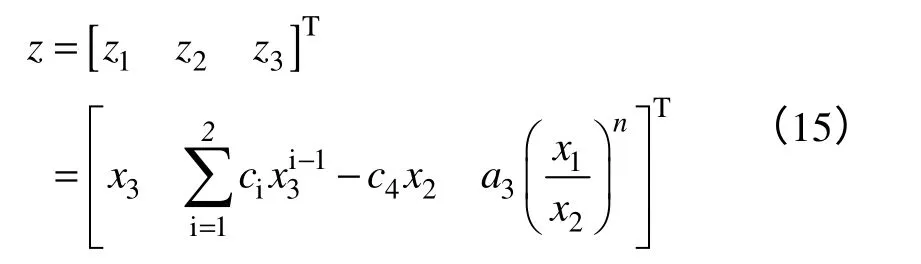
式中，幂次n可以取任意值。

采用基于中心流形理论的零动态计算方法，原非线性系统状态方程式（13）经过变换得到线性系统状态方程式（16）：

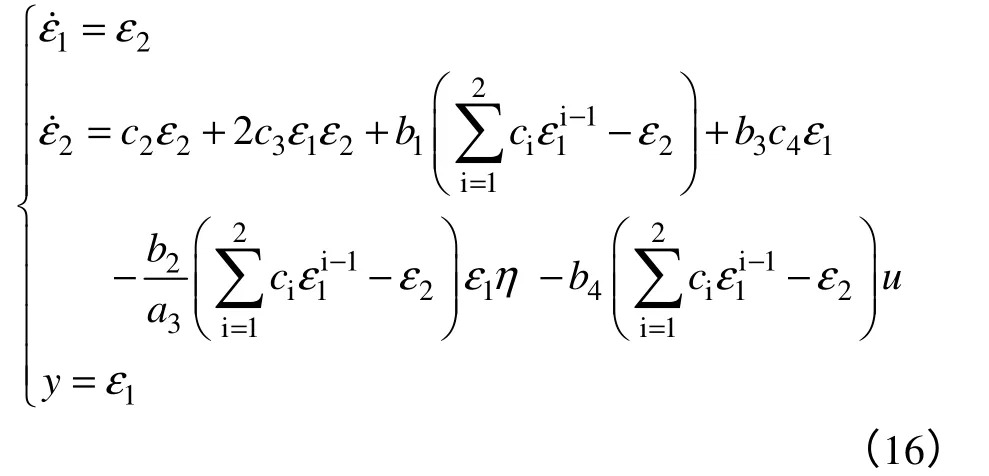
式中，ε1=z1,ε2=z2,η=z3。若记ε=[ε1,ε2]T，则上述线性系统可进一步写为

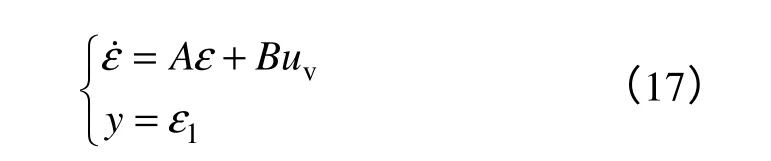
式中，非线性系统的输入变量u与线性系统的输入变量uv具有以下关系

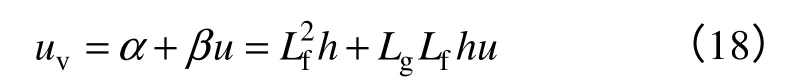
其中

2.4 滑模控制器设计

针对系统

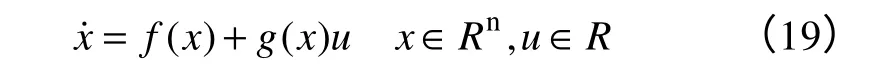
其中x满足=xi+1,i= 1,… ,n-1。滑模面设计为

式中，x为状态向量，C=[c1…cn-11]T。

参数ci应该满足多项式pn-1+cn-1pn-2+…+c2p+c1，其中p为Laplace算子[14]。

风力发电机一般以发电机转速ωg作为控制目标，风电系统根据风速和输出功率等条件可以得到发电机参考转速ωref，设为转速误差，则有

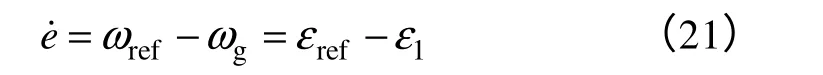
可取线性切换函数为

则可以得到滑动模型运动方程

因此，只要保证ki＞0，i=0,1，即可保证滑动模态渐进稳定，调节k的取值，可调节滑动模态的动态品质。

取Lyapunov 函数为

则

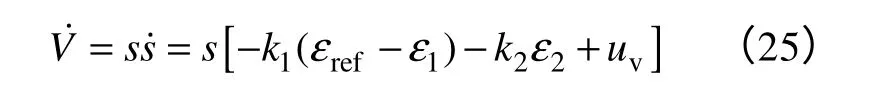
采用新型指数趋近律，有

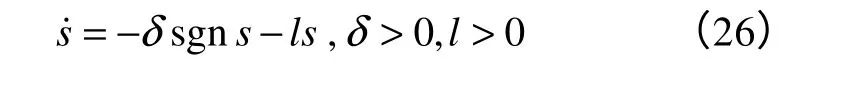
可得到线性系统的输入变量uv：

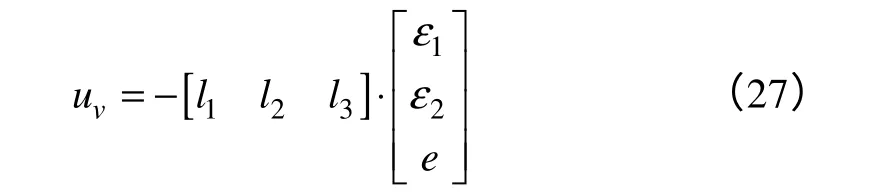
所以由式（18）可得到

上述分析可作出最大风能跟踪的控制框图4。

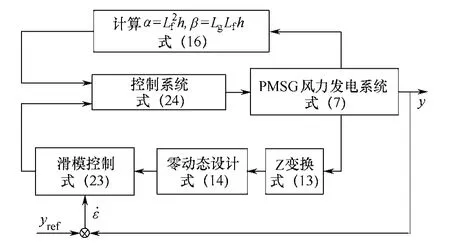
图4 风力发电系统控制系统框图

3 仿真结果分析

为了验证提出算法的有效性，本文基于Matlab/Simulink 建立了仿真模型，主要参数见表1。

表1 系统主要参数

3.1 阶跃风下的仿真图

阶跃风下，初始时，风速v=6m/s在30s后阶跃到v=9m/s，在65s后下降到v=8m/s。

图5为最大风能利用系数Cp在两种控制方法的对比仿真图。其中，虚线为PI控制，实线为基于中心流形理论零动态设计的滑模控制。

图6为基于两种控制方法下实际转速和参考转速的对比仿真图。

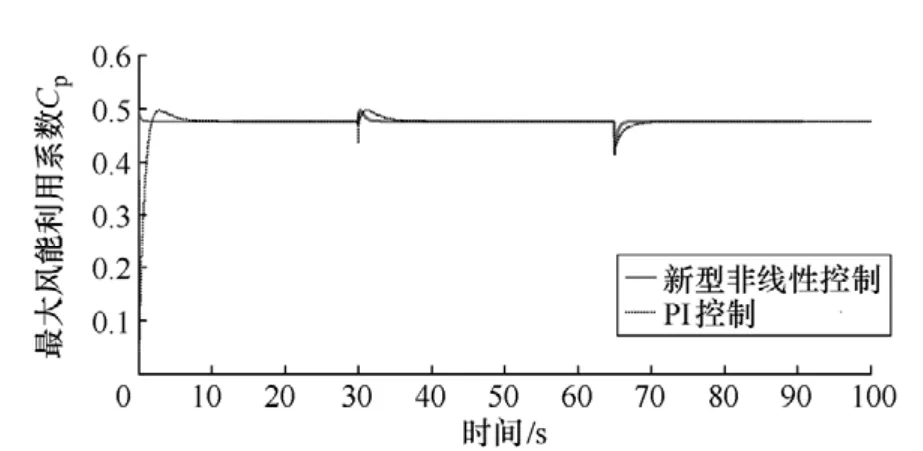
图5 最大风能利用系数Cp 在两种控制方法的 对比仿真图

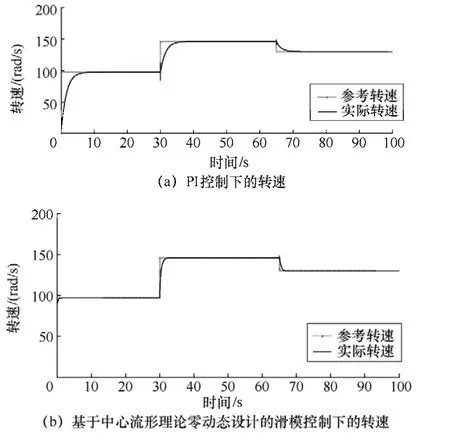
图6 两种控制方法在阶跃风下的转速对比

从图中可以看出，在PI控制中，其转速响应时间明显滞后于基于中心流形理论零动态设计的滑模控制的响应时间。

3.2 组合风下的仿真图

在组合风速中，设基本风速vb=6m/s 阵风的最大值vgmax=2m/s、渐变风vrmax=2m/s 和和噪声风的变化范围vn=±2m/s。其风速曲线如图7所示。

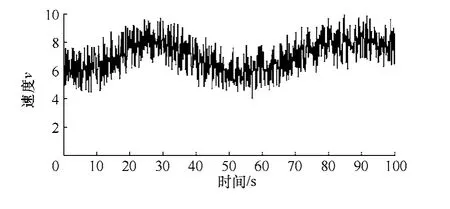
图7 组合风

在组合风速下，两种控制方法的转速曲线如图8所示。

图8 两种控制方法在组合风下的转速对比

图中可以看出，在组合风速下，与PI 控制相比较，基于中心流形理论零动态设计的滑模控制下的电机转速震荡较弱，且波动较小，恢复速度快，充分说明了该新型非线性控制方法具有良好的动态性能和鲁棒性。

3.3 转速与输入阻抗关系

在本文中，网侧相当于负载，简化为等效可变电阻Rs和定电感Ls表示。Rs的不同也会影响着转速的变化。

图9是基于中心流形理论零动态设计的滑模控制下，转速与输入电阻Rs关系。

图9 转速与输入阻抗关系

从图中可以看出，由于风机重负载的阻碍作用，控制输入Rs越大时，转速的波动越小，抗干扰能力越强。

综上，通过仿真可以验证本文针对直驱永磁同步电机，提出的基于中心流形理论的零动态设计滑模变结构控制方案是正确可行的，该控制方案不仅具有响应速度快，超调小等优点，而且具有较强的抗扰性能。

4 结论

本文针对实现最大风能跟踪的问题，提出基于中心流形理论的零动态设计与滑模变结构相结合的控制策略。阶跃风和组合风下，与PI 控制相比，该控制器明显提高了系统的动态性能，而且阶跃响应迅速，超调较小，抗扰动性能好，具有较强的鲁棒性。

[1] 李建林.风力发电系统低电压运行技术[M].北京: 机械工业出版社,2009: 67-69.

[2] 乐江源,谢运祥,洪庆祖,等.Boost 变换器精确反馈线性化滑模变结构控制[J].中国电机工程学报,2011,31(30): 16-23.

[3] 孙永清,张超,翟俊峰,等.永磁同步风力发电系统最大功率跟踪控制策略及仿真分析[J].水电能源科学,2012,30(9): 192-194,157.

[4] Savaresi S M.Exact Feedback Linearization of Fifth Order Model Synchronous Generators[C].IEEE proceedings.Control theory and applications.1999,146(1): 53-57.

[5] 陈思哲,吴捷,姚国兴,等.基于微分几何的风力发电机组恒功率控制[J].控制理论与应用,2008,25(2): 336-340.

[6] Cutululis N A,Ceanga E,Hansen A D.Robust multi- model control of an autonomous wind power system[J].Wind Energy,2006,9(5): 399-419.

[7] 王利兵,毛承雄,陆继明,等.基于反馈线性化原理的直驱风力发电机组控制系统设计[J].电工技术学报,2011,26(7): 1-6,20.

[8] Nicolas Antonio Cutululis.Feedback linearization control of wind power system 2004 ISSN 1221-454X.

[9] Hassan K K.Nonlinear systems[M].Third Edition.New Jersey,USA: Prentice Hall,2002: 430-438.

[10] 耿华,许德伟,吴斌,等.永磁直驱变速风电系统的控制及稳定性分析[J].中国电机工程学报,2009,29(33): 68-75.

[11] Carr J.Application of center manifold theory[M].NewYork: Springer-VerlagBerlin: Heidelberg,1981.

[12] 卢强,孙元章.电力系统非线性控制[M].北京: 科学出版社,1993: 94-99.

[13] Li Zhong,Zhang Bo.Bifurcation analysis of the Permanent-Magnet synchronous motor models basedon the center manifol theorem[J].Control Theory and Applications,2000,17(3): 317-320.

[14] 刘金琨.滑模变结构控制Matlab 仿真[M].2 版.北京 : 清华大学出版社,2008: 83-87.