交直流电力系统暂态过程中同步发电机 阻尼转矩系数的计算
吴学苹 江宁强
(南京理工大学自动化学院电气工程系,南京 210094)
同步发电机的阻尼转矩系数对电力系统的暂态稳定性有重要影响。多摆失稳与阻尼转矩的联系在稳定研究中已引起关注。利用BCU 法(Boundary of stability region based on Controlling Unstable Equilibrium Point method)分析系统的暂态稳定性时,需满足单参数横截性条件,而该条件是否成立与阻尼大小有关[2]。阻尼系数存在一个临界值,当大于临界值时,系统完全稳定。因此暂态过程中阻尼转矩系数的研究具有重要意义。
由于计算速度的要求,大规模电力系统稳定分析中部分发电机需采用简化模型。模型中阻尼系数设置为常数,来模拟阻尼绕组、网络耗散特性、负荷、稳定控制装置等多种阻尼因素的影响。而阻尼系数的取值往往根据经验选取[1],其准确值尚难以确定。这是因为即使发电机选用详细模型,阻尼转矩蕴含在电磁转矩中,仍难以准确获得阻尼转矩。
电力系统所经受的扰动可分为小扰动和大扰动。小扰动情况下,系统分析时可将系统方程线性化。其稳定平衡点不会发生变化。而大扰动下系统方程是非线性的,扰动前后稳定平衡点可能不同。 早期阻尼转矩系数的研究主要针对小扰动模型。文献[3]设同步转矩系数和阻尼转矩系数为常数,提出了一种转矩分解方法—breaking algorithm。文献[4-5]将电磁转矩增量分解为阻尼转矩增量和同步转矩增量,通过仿真或实验数据求取同步转矩系数及阻尼转矩系数。文献[6]利用Prony 分析法计算了多机系统的阻尼转矩系数。
由于大扰动情况下电力系统是高阶非线性的,故小扰动分析法已不适用。暂态过程中关于阻尼系数计算的研究较少。文献[7]利用派克方程推导了单机无穷大系统暂态过程中阻尼系数的解析表达式。文献[8-9]假设功角作稳态正弦大振荡,分解得到同步发电机的阻尼转矩系数,指出阻尼转矩系数不是常数。文献[10]利用多项式逼近定理得到暂态过程中发电机的阻尼转矩系数。
上述研究都是以交流系统为研究对象,由于电力系统已经由纯交流系统发展为交直流混合电力系统。本文在文献[10]的基础上利用多项式逼近法求取交直流电力系统暂态过程中同步发电机的阻尼转矩系数。并利用文献[4-5]中的方法来检验本文方法的正确性。
1 大扰动下同步发电机阻尼转矩系数计算
1.1 阻尼转矩系数的数值分析方法
多项式逼近定理可实现对有界闭区间上连续多变量函数的有效逼近。文献[10]给出了利用多项式逼近法(Weierstrass 逼近定理)计算阻尼转矩系数的详尽过程。在此不再详述,直接给出暂态过程中电磁转矩Te的逼近表达式。
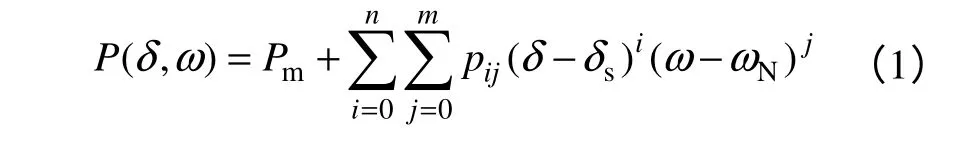
式中,Pm为机械功率,δs为稳定平衡点角度,ωN为额定角速度。n、m分别为角度差和角速度偏差的最高指数,pij为相应的多项式系数,且p00=0。
当n、m和pij确定后,可得到电磁转矩的近似表达式,并使逼近误差满足:

如果式(2)中的ε足够小,则令Ps=P(δ,ωN),可近似得到同步转矩Ts,进而可以获得阻尼转矩的近似值,并计算出阻尼转矩系数:
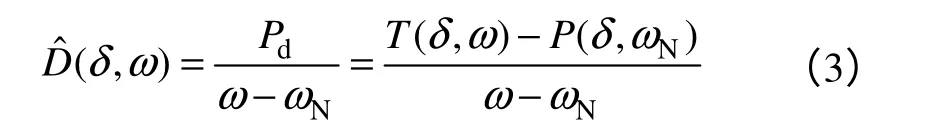
由以上分析可知,计算阻尼转矩系数需要设定够小的逼近误差ε,然后确定式(1)所示多项式函数的指数n和m,以及多项式系数pij。
下面介绍大扰动后,沿故障后轨线计算阻尼转矩系数的步骤。设故障清除时间为tcl:
(1)在故障中轨线上取2k1+1 个点作为故障后轨线的起始点,即xh01=x(tcl+h1Δt1),h1=-k1,…,-1,0,1,…,k1,Δt1=tcl/100。
(2)通过仿真获得2k1+1 条故障后轨线,在每 条故障后轨线上采样k2个点,记录每个采样点的转子角、转子角 速度和电磁转矩,即
(3)确定多项式系数pij。对于给定的一组指数n、m,可由采样值得到(2k1+1)×k2个方程
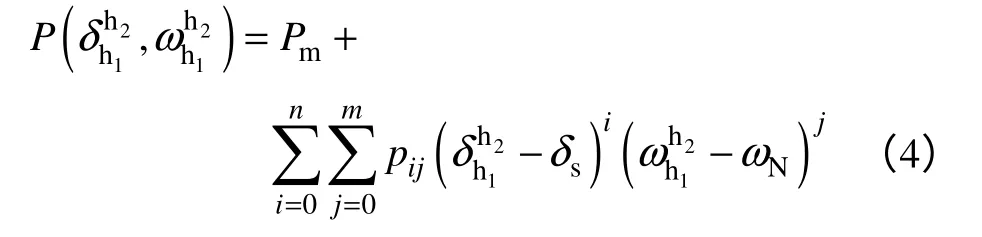
通过解式(5)所示的最小值问题,可确定(n+1)×(m+1)-1 个多项式系数pij。
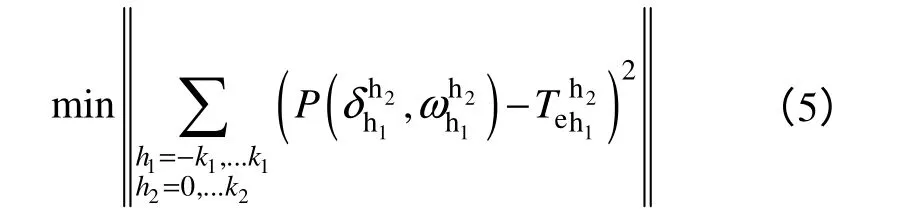
设x=[p01,…,p0m,p10,…,p1m,…,pn0,…,pnm],上述最小值问题利用最小二乘法求解可得
式中,矩阵A、b示于本页底部。
(4)系数pij确定后代入式(1)得到电磁转矩的逼近值P(δ,ω),判断逼近误差是否满足式(2)。若满足,则第(3)步中给定的指数n、m可作为电磁转矩逼近多项式(1)中的最大指数。如果不满足则返回第(3)步,重新设定新的n、m值。
(5)n、m确定后,对于给定的故障切除时间,采用故障后仿真数据,通过式(1)计算P(δ,ω)。
(6)令多项式(1)中的角速度为额定角速度,得到Ps,作为同步转矩Ts的近似值。
(7)从Te中减去Ps,得到阻尼转矩近似值Pd。
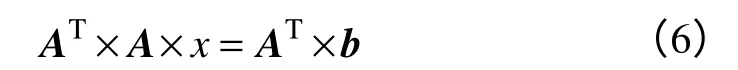
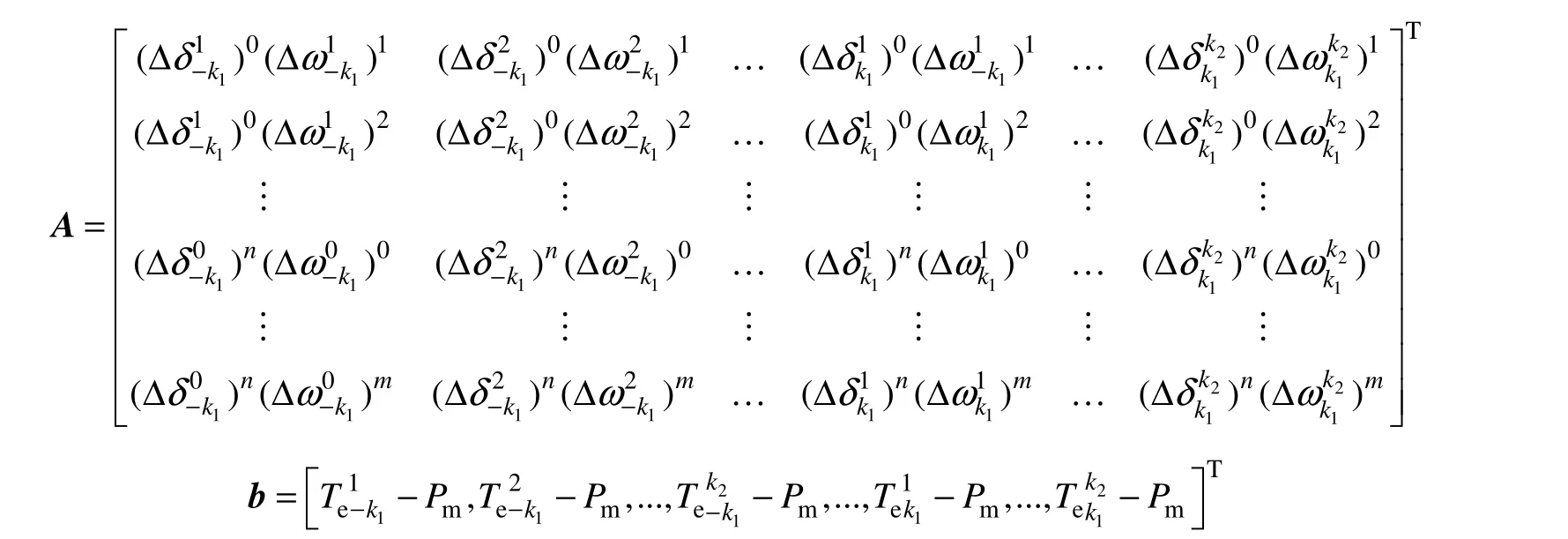
(8)用阻尼转矩近似值除以角速度差,得到暂态过程中的阻尼转矩系数D。
1.2 算例分析
本文研究的交直流系统如图1所示。发电机通过两条并联线路,经理想变压器与无穷大母线相连,一条直流线路与交流输电线路并联。系统中交流部分参数见文献[1]。发电机初始电压V=1.05,输入机械功率Pm=0.8。负荷p=0.6,q=0.4,为恒功率负荷。发电机模型采用七阶模型,考虑一阶励磁系统作用。直流输电系统参数见文献[11]。直流输电系统采用准稳态模型。整流侧采用定电流控制Ids=0.1,逆变侧采用定熄弧角控制,γ=22°。定电流控制调节器的比例和积分参数为:K1=0.5,T1=2。定熄弧角控制调节器的比例和积分参数为:K2=0.5,T2=2。
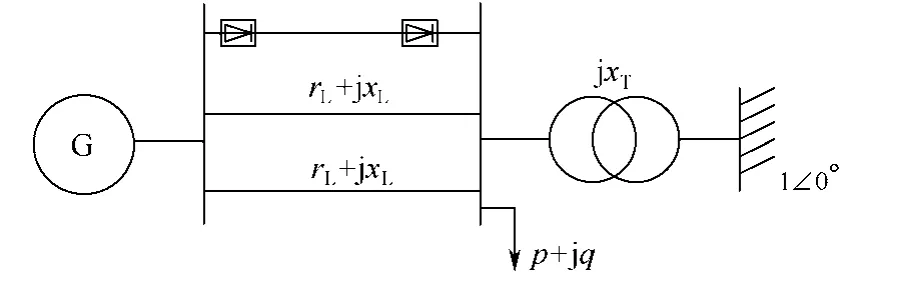
图1 单机无穷大交直流电力系统
上述系统经受快关气门扰动,扰动持续时间为0.05s,故障后仿真15s。仿真计算得到系统的电磁转矩Te、功角δ、角速度ω曲线如图2所示。
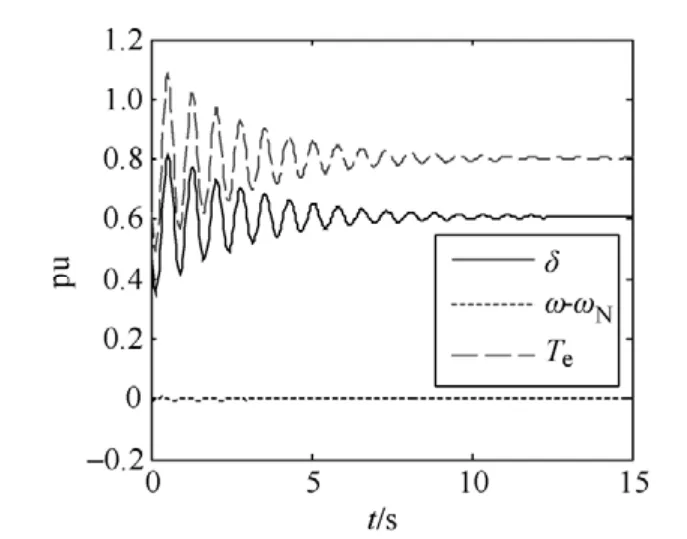
图2 交直流系统电磁转矩、功角、角速度差的仿真曲线
由图2可知系统在上述扰动下是暂态稳定的。系统各物理量均恢复到原平衡点。
利用多项式逼近法对电磁转矩进行分解,最终得到发电机的阻尼转矩系数如图3所示。
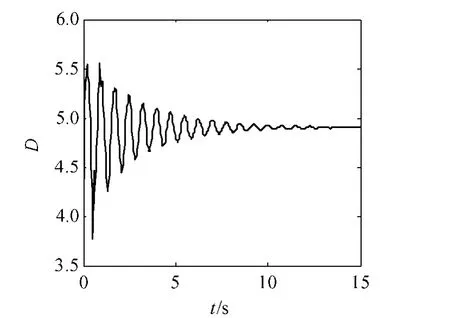
图3 交直流系统暂态过程中发电机的阻尼转矩系数
由图3可知在暂态过程中发电机的阻尼转矩系数D是变化的,在暂态初期波动范围较大,最大值为5.6,最小值为3.8。t>5s 后波动范围较小,随着系统的稳定阻尼转矩系数最终值稳定在4.9 附近。由分析可得暂态稳定系统的阻尼转矩系数在暂态过程结束后其值趋向于常数。
本文所采用的多项式逼近法没有采用线性化假设,故其可用于大扰动和小扰动的阻尼转矩系数计算。因尚无其他算法检验暂态过程中发电机阻尼转矩系数计算的正确性。由图2可知t>5s 后发电机各物理量波动较小,可视5s后的动态过程为小扰动。利用小扰动的阻尼转矩系数方法计算该算例t>5s后发电机的阻尼转矩系数,与本文方法得到的结果比较。间接验证本文方法的正确性。
2 阻尼转矩系数计算结果的讨论
文献[4-5]提出了系统受到小扰动时电磁转矩系数的算法。在系统动态过程中将电磁转矩增量分解为阻尼转矩增量和同步转矩增量。阻尼转矩增量与角速度变化成比例,同步转矩增量同功角变化成比例。并假设阻尼转矩系数和同步转矩系数均为常数。因此,转矩增量可表示为

式中,ΔTe为电磁转矩变化量;Ks、Kd分别为同步转矩系数和阻尼转矩系数;Δδ、Δω分别为功角变化量和角速度变化量。
利用最小二乘法通过动态仿真或实验数据求取电磁转矩系数。Ks、Kd由式(8)、式(9)求得
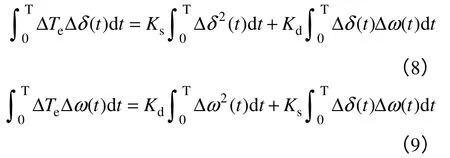
通过对时域仿真得到的ΔTe、Δδ、Δω进行数值积分得到式(8)、式(9)中的各积分项。进而得到同步转矩系数Ks和阻尼转矩系数Kd。
上述算法能够计算出小扰动下发电机的同步和阻尼转矩系数。采用本文提出的方法对大扰动和小扰动情况均适用,故对小扰动的计算结果应当与上述方法一致;否则,难以保证大扰动下阻尼转矩系数计算结果的正确性。
下面首先采用上述算法计算大扰动振荡基本平息后的电磁转矩系数。利用故障清除后5~15s 的仿真数据,计算本文2.2 节算例中同步发电机的阻尼转矩系数。其结果示于图4。由图4可得5~15s 之间Kd的值基本一致,其值大小在4.9 左右。说明该算法对本文算例是有效的。
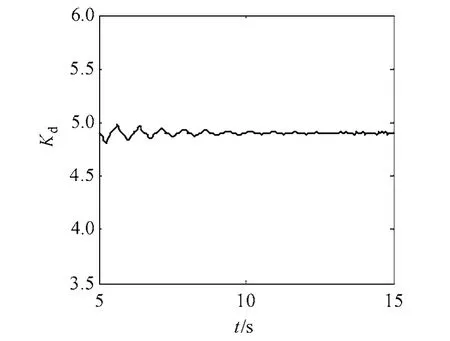
图4 小扰动算法得到的t>5s 后的阻尼转矩系数
将图4与图3中t>5s 后的阻尼转矩系数进行比较。由图3可见,t>5s 后的波动范围较小,并逐渐趋于4.9。两种算法得到的结果相差小于0.01,可以认为结果是一致的。间接验证了该文方法在暂态过程中发电机阻尼转矩系数计算的有效性。
3 结论
本文利用多项式逼近法求取交直流电力系统暂态过程中同步发电机的阻尼转矩系数,结果显示,暂态过程中阻尼转矩系数不是常数。对于稳定系统,随着振荡逐渐平息,阻尼转矩系数也趋于一个稳态值。采用多项式逼近法计算得到的阻尼转矩系数的最终值,与利用小扰动模型阻尼系数计算方法计算暂态基本平息后的阻尼转矩系数基本一致,验证了本文方法的正确性。
[1] Kundur P.Power system stability and control[M].New York: Mc Graw-hill,1994.
[2] Alberto L C,Bretas N G.Required damping to assure multiswing transient stability:The SMIB case[J].International Journal of Electrical Power&Energy System,2000,22(3): 179-185.
[3] De Mello F P.Concordia C.concepts of synchronous machine stability as affected by excitation control[J].IEEE Transaction on Power Apparatus and System,1969,88(4): 316-329.
[4] Alden R H,Shaltout A A.Analysis of damping and synchroning torques part I-A general calculation method[J].IEEE Transactions on Power Apparatus and Systems,1979(5): 1696-1700.
[5] Alden R H,Shaltout A A.Analysis of damping and synchroning torques part II-A general calculation method[J].IEEE Transactions on Power Apparatus and Systems,1979,PAS-98(5): 1701-1708.
[6] 李鹏,余贻鑫,孙强,等.基于Prony 分析的多机系统电磁转矩系数计算[J].电网技术,2006,30(10): 39-44.
[7] 张钰,王英.杜阿美尔积分法求阻尼转矩和阻尼功率[J].太原理工大学学报,1998,29(2): 90-93,97.
[8] 汤蕴璆,王艳萍.功角作正弦大振荡时同步电机的整步转矩和阻尼转矩系数[J].哈尔滨电工学院学报,1990,13(1): 1-14.
[9] 王艳萍.功角作正弦大振荡时定子电阻对同步电机整步转矩和阻尼转矩系数的影响[J].哈尔滨电工学院学报,1991,14(2): 129-132.
[10] Jiang Ningqiang,Chiang HD.Numerical investigation on the damping property in power system transient behavior[J].IEEE Transactions on Power Systems,2013,28(3): 2986-2993.
[11] 徐政.交直流电力系统动态行为分析[M].北京: 机械工业出版社,2004.

