微网故障检测关联规则挖掘算法研究

朱文灏 郭其一

（1.同济大学电子与信息工程学院，上海 201804；2.上海施耐德低压终端电器有限公司，上海 201109）

在电力电子和现代控制理论的发展背景下，微电网第一次被R.H.Lasseter 教授于2001年提出[1]。这是一种新型的基于信息网络的能量供应和管理技术，有利于能源可持续发展、需求侧管理和各种能源最大限度地使用[2]。计算机凭其快速的计算能力被广泛用作微网故障分析，它能快速的、准确的给出分析结果，并为调度决策提供合理的操作参考[3]。

微网系统故障往往具有复杂性，传统的数学方法不能描述具有多重故障类型的模型[4]。随着人工智能技术的发展，尤其是在仿真人类处理各种问题的能力方面的发展，使其被许多学者广泛接受，并成功应用于电力系统故障检测领域。C.A.Petri 发展了Petri 网络数学模型，这个模型适用与小范围内具有稳定结构电网的故障检测[5]。但同时，这个模型在设备数量经常变化的大范围电网应用上存在许多局限性。为了减少故障样本记录和无价值的条件特征，Z.Pawlak 将粗糙集理论应用于电网故障检测[6]。LA Zadeh 提出了一种基于模糊理论的电网故障检测模型，来处理非确定性问题[7]。但当存在许多不确定性因素时，问题仍很难求解。Pitts 将人工神经网络应用到故障检测中，该方法便于将故障类型和故障信号的逻辑关系分清楚[8]。但人工神经网络在应用前需要进行训练，此训练的收敛速度缓慢。该方法只有在系统结构不变的情况下适用。Lee 提出一种基于贝叶斯网络的模型[9]，和传统故障检测方法相比，这个模型具有清晰的逻辑和快速的处理速度，以及强壮的学习能力和良好的容错性。但它也存在缺点，比如，每个节点的条件概率分布不是由贝叶斯网络定义，而是由来自经验的统计分析技巧所决定。在传统故障检测方法的基础上，本文提出了一种基于贝叶斯网络的关联规则挖掘和频繁项集优化的算法。

1 关联规则挖掘算法改进

1.1 Aprior 算法简介

Apriori 算法是一种用于搜索频繁项集的基本算法，该算法采用逐层搜索的迭代方法，也就是用k-项集搜索(k+ 1)-项集[10]。该算法通过频繁项集属性中的先验知识，首先生成频率1-项集L1，然后生成频率2-项集，直到生成某频率的r项集Lr为空。

在第k次循环中，候选的k-项集第一次生成了Ck集。每个候选项由一个(k- 2)-节点生成，此节点处在两个只有一个不同项（此项属于Lk-1）的频繁项集中。在Ck中的项集就是频繁项集的候选项，并且最后的频繁项集Lk一定是Ck的子集。为了决定其是否可加入Lk，须在数据库事务中核实每个元素，该算法由于存在可观的输入、输出计算量，因而其性能得到限制。

Apriori 算法基本步骤是：首先，迭代识别所有的频繁项目集，要求频繁项集的支持率不低于用户设定的最低值；其次，从频繁项集中构造支持度和可信度不低于用户设定的最低值的强关联规则。

1.2 Apriori 算法改进

在生成项集Ck的每步前，Apriori 算法有赖于相应频繁k- 1项集，并搜索数据库来计算每个候选项集的支持度，以便生成频繁项集，这需要花费许多时间和空间。因此，生成很小的候选项集的过程在提高频繁项集搜索效率方面起到重要的作用。而且，在Apriori 算法中，候选集Ck和Lk-1会在Ck具有很大可能性的地方同步生成。Hash 技术能去除那些不需要的候选项来降低Ck的可能性，因而可以降低时间和空间消耗并增强算法的效率。

在Apriori 算法中，当在D中的事务和在I中的项目数据量很大时，在L1中的项目数也会变的很大，假设为m，那么联合生成的候选2-项集C2生成数为因此，支持度的计算量会变得十分巨大。

运用Hash 技术的主要目的是解决这个冲突。本文采用二维Hash（散列）函数来避免这个冲突。在项目集I= {I1,I2,… ,Ik,… ,Im}中的每个项目I k(k= 1,2,… ,m)具有一个顺序值：1,2,… ,k,… ,m。order(x)和order(y)表示为在候选项集2-中的项目x和y的顺序值。则二维散列函数为，

此处，

p1≠p2，且其是相对质数。

若p1和p2的值很大，散列表能覆盖更多空间；若它们很小，则会导致冲突。因而，p1和p2须根据项目数调整并定义最小支持度。

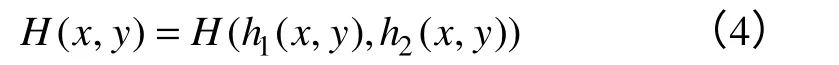
h1(x,y)和h2(x,y)为H(x,y)下标。当散列数映射出1 个单位，则计数值增加1。

在扫描数据库和生成L1的同时，每个2-项目集在每项事务中被二维散列函数计数。在数据库扫描完后，L1和二维散列表均被获得，且表内每个单位的值是一个事项的累积值。如果事项数值等于或大于最小minsup，则2-项目集属于L2，否则它不为2-频繁项集。

2 基于贝叶斯方法和关联规则挖掘算法的微网故障检测

2.1 基于贝叶斯网络的样本训练

若有一个新的训练样本，则能在现有样本数据集中学习并将新数据归类。此贝叶斯理论和本文的任务需求一致。

此公式能表达成贝叶斯等式。

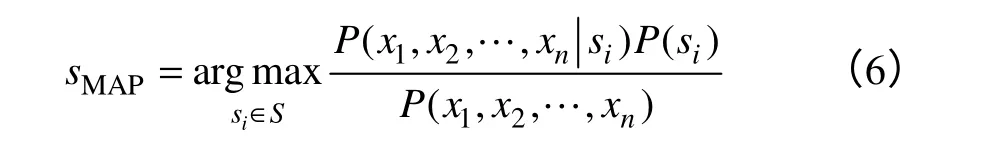
可以通过式（6），根据训练数据得到估计值。其实，预测出每个P(si)较容易，只要从训练数据中计算每个目标值si的频率即可。然而，如果没有收集相当大数量的训练数据，则不能通过此方法预测 不同的因为此项数量等于可 能的例子数和可能的目标值的乘积，此方法需要大量的训练项集。为了获得合理的估计，每个样本须在样本空间出现多次。

贝叶斯算法有一个简单假设：若给定样本的目标值，则x1,x2,… ,xn的共同概率等于每个单一属性的概率乘积。

将此式代入式（6），则可得在贝叶斯算法中的公式

此处sNB是从贝叶斯算法计算得到的目标值。在贝叶斯算法中，从训练数据中估计得出的不同的的项目数只是不同的目标数和特征值的乘 积，这个数比的总数小很多。

如果用此方法计算的某一条件概率为0，则无论其它特征概率值为多少，其值始终为0。这些特征是独立的，所以目标值会被它们的连续乘积所影响。为避免在有限样本中存在的概率为0 的问题，采用m-估计法进行优化，以便使得分类更精确。m-估计定义如下：

此处，v表示为分类ni中样本数，vx表示为mi的样本数（同分类ni样本相似）；u表示为与样本相关的特征；p为测试器指定的参数。如果训练集为 0，则因而，在分类ni中特征mi的先 验概率为p。样本的等价值决定了概率p和v x/v之间的关系。

2.2 微网故障检测具体过程

本文采用基于关联规则挖掘和贝叶斯网络算法的微网故障检测方法，同时考虑早期故障数据冗余和由于微网故障检测不确定性导致的偏差。具体流程如图1所示。

图1 微网故障检测流程图

根据此流程图，具体算法如下：

1）从保护器或断路器处采集的动作信息作为条件特征，故障元件作为决策特征，选取训练样本集，并根据过去的故障样本建立初始决策表S；将其输入输入数据库，以生成关联规则挖掘目标的数据资源。

2）运用关联规则交互挖掘初始决策表，减少多余目标和特征。应注意到，当支持度和可信度门限值低时，会生成大量的弱关联规则并且挖掘时间会变长。反之，则一些有价值的关联规会被忽略。实际上，可采用较小的样本数量进行交互挖掘迭代，通过不断地调节门限值来确定合适的门限值。然后，将此方法用于以支持度和可信度为目标的大数据处理。

3）贝叶斯网络初始化。

4）采用改进后的Apriori 算法对新生成的特征集进行数据挖掘，得到符合支持度限值的频繁项集；对每个频繁项集建立关联规则，并选取其最小可信度和关联度大于1 的强壮项集。忽略支持度小于最小值的项集，从而减少搜索空间。

5）建立基于步骤（2）关联规则的贝叶斯模型：

对于每条规则，X⇒C并且从NewRules中依次提取；提取与X相应的可信度，并将X⇒C加入贝叶斯网络。

6）将故障区域值C(c1,c2,… ,cn)（指决策表内的决策特征）作为贝叶斯网络的父节点，并将已减 少的关联规则组Rmai(x1,x2,… ,xn)中的条件特征作 为子节点，建立贝叶斯网络。

7）训练每个节点，并计算每个父节点的先验概率和每个子节点的条件概率。

8）实时故障检测。

给出的实时故障检测信息为X(x1,x2,...,xn)，包 括完整的信息、非完整的信息、甚至错误的信息。采用已训练的贝叶斯网络，对这些信息进行诊断，并计算可能的故障区域的概率。

最后，对得到的可能的故障区域概率进行筛选，并将最大概率的故障区域Ck作为最终诊断结果输出。

3 仿真实验

为验证此改进算法的有效性，本文进行了仿真实验。实验选用7 个电网故障样本，此样本分别具有条件特征：断路器B1、B2、B3；过电流保护C1、C2、C3；距离保护R1。每个特征值为0 或1，分别代表断路器的合和分状态。决策特征为故障区域，通常表示为线路S1、S2、S3，见表1。

表1 初始微网故障检测决策表

上述故障信息经基于贝叶斯网络和关联规则的检测模型进行数据挖掘后，得到的结果见表2。

表2 微网故障检测结果表

图2记录了当前模型检测结果和实际结果之间的误差。

从表2和图2可见，基于贝叶斯网络和关联数据挖掘的检测模型能较好地应用于微网故障检测，并且检测误差远远低于Apriori 算法和贝叶斯算法。

图2 诊断误差的统计结果比较

4 结论

微网具有电流双向贯通和局部短路承受能力低的特点，传统的配电网技术不再适用于微网的发展。鉴于此，本文提出了一种改进的基于贝叶斯模型和关联规则挖掘的检测模型。仿真实验结果表明此模型能有效地且大量地减少传统算法在配电网故障检测中产生的误差。

[1] 周建萍,朱建萍,徐司聪.微网孤岛运行时短路故障检测的仿真研究[J].中国电力,2014,47(3): 85-89.

[2] 杜敏杰,马善钊,王建国,等.基于核密度估计的实时SVDD 算法与电路故障检测应用[J].计算机测量与控制,2014,22(4): 1039-1041,1045.

[3] 张哲军.引入推理模型的大型电网设备的故障检测方法[J].科技通报,2014,30(2): 111-113,135.

[4] 杜华.基于关联规则的船舶供电系统故障检测方法研究[J].计算机测量与控制,2014,22(1): 233-235.

[5] 张咪.一种远端故障检测方案的设计与实现[J].电子技术应用,2013,39(12): 126-128,131.

[6] 张海涛,高锦宏,吴国新,等.蚁群优化算法在风电偏航故障检测中的应用[J].可再生能源,2013,31(11): 48-50,55.

[7] 原艳红.大型煤炭机电设备的故障检测方法研究[J].计算机仿真,2013,30(8): 380-383.

[8] 郑树松,李红梅.电动汽车PMSM 驱动系统的故障检测[J].微电机,2013,46(8): 55-59.

[9] 王娟,张瑾.高压电力计量系统故障诊断与应用研究[J].科学技术与工程,2013,13(19): 5617-5620.

[10] 杜敏杰,蔡金燕.基于样本约简的实时SVDD 算法与电路故障检测应用[J].微电子学与计算机,2013,30(7): 86-90.