民航应急救灾物资调度优化仿真研究

邵 荃，梁斌斌，朱 燕，张海蛟，张金石

(1.南京航空航天大学 民航学院，江苏 南京210016;2.中国民用航空新疆管理局，新疆 乌鲁木齐820016)

民航应急物资调度是指利用民航运输机进行应急物资调度的过程，因其速度快、航程远的特点在应急救援体系中起着重要作用。一般而言，民航应急物资调度需要多机场、多物资协同参与，利用有限运力将有限的物资运抵灾区。国外学者针对地面应急物资调度问题作了大量研究，普遍采用优化算法进行求解［1-4］;国内学者针对多目标调度问题进行了研究［5-6］，设计了不同的路径优化数学模型［7-8］。OZDAMAR［9］基于航路管理程序(RMP)对直升机应急物资调度问题进行求解。祁明亮等［10］研究了车辆与直升机联合调度问题。可以看出，现有研究大多是关于车辆或者直升机应急调度，对民航应急物资调度的研究十分有限。不同于前两种调度方式，在民航应急物资调度中，机场无法保障的机型无法飞往该机场，短航程机型无法进行远距离运输，飞行地面保障时间无法忽略，这些特点决定了有必要对民航应急物资调度进行单独研究。遗传算法是解决物资调度问题的常用优化算法之一，但其稳定性较差且容易早熟。由其衍生出的完整元胞遗传算法有较好的稳定性和抑制早熟的能力［11-12］。当前，少有研究采用元胞遗传算法求解应急调度问题，常用的元胞遗传算法极少考虑个体适应度对元胞状态演化的影响，在寻优能力和收敛性方面均有较大缺陷，有待进一步改进。

根据民航应急物资调度的特点，建立不同于地面车辆和直升机调度的多机场多物资联合调度模型，并基于适者生存的生态法则提出一种与个体适应度相关的元胞状态演化规则，可有效提高算法的寻优能力和收敛性能，便于更好地求解模型。实例表明，该模型合理可行，算法较标准遗传算法和传统元胞遗传算法均具有优势。

1 民航应急救灾物资调度原理

民航应急救灾物资调度问题可描述为：存在若干个救灾机场(运出物资)和若干个受灾机场(接收物资)。当灾情发生后，飞机在救灾机场装载物资，运输物资前往具有保障能力的受灾机场，卸载物资之后返回任一具有保障能力的救灾机场，如此往返直至救灾任务结束。为方便理论建模，假设物资为统一规格的包装单元，飞机总是装载整数个单元的物资;运输过程中飞机总是以巡航速度飞行。该问题的数学表达式如下：

救灾机场集合D={d1，d2，…，dn}，表示共有n个救灾机场，di表示第i个救灾机场;

受灾机场集合E={e1，e2，…，em}，表示共有m个受灾机场，ej表示第j个受灾机场;

应急物资种类集合C={c1，c2，…，cl}，表示共有l种应急物资，cI表示第I种应急物资;

救灾机场物资储备量矩阵，dmiI表示应急物资I在救灾机场i的储备数量：

受灾机场物资需求量矩阵，emjI表示应急物资I在受灾机场j的需求数量：

受灾机场物资需求紧要度矩阵，ujI表示物资I在受灾机场j的紧要程度，其中…，m。

可用飞机集合A={A1，A2，…，Ap}，表示共有p架飞机执行调度任务，Ah表示第h架飞机;

飞机载运量集合L={L1，L2，…，Lp}，Lh表示第h架飞机的载运量;

飞机航程参数集合R={R1，R2，…，Rp}，Rh表示第h架飞机的航程;

飞机巡航速度集合v={v1，v2，…，vp}，vh表示飞机h的巡航速度;

飞机地面保障时间t={t1，t2，…，tp}，th表示飞机h所需的地面保障时间;

机场飞机可用度矩阵：

(Oij=1 或0)，其中Oij=1 表示机场j可以保障飞机i，Oij=0 表示机场j不能保障飞机i。表示救灾机场i处飞机h的可用度，Oehj表示受灾机场j处飞机h的可用度;

航线距离集合r={rij|i=1，2，…，n;j=1，2，…，m}，rij表示救灾机场i到受灾机场j的航线距离;

飞机h的一次飞行任务τs包括出发的救灾机场、运载的物资种类及数量和抵达的受灾机场。飞 行 任 务表示飞机h在飞行任务τs中从救灾机场i向受灾机场j运载第I种物资的数量;

应急调度方案φ 由所有飞机的调度方案组成，即φ= {φ1，φ2，…，φp}，其中φh表示飞机h的调度任务序列，即φh= {τ1，τ2，…，τN}，表示任务序列φh由N次飞行任务组成;

应急调度方案φ 的完成时间为Tφ，飞机h执行其调度任务序列φh的时间为：

如果任务序列中存在无法保障飞机h的机场则对应的任务完成时间为无穷大(Th=∞)。由此可得到整个调度方案的完成时间Tφ=max{Th}(h=1，2，…，p)。

救灾效果满意度指数γ 表示运输方案能够满足受灾需求的程度。统计受灾机场物资需求量矩阵EM中各个物资需求元素被满足的程度。元素emjI被满足的程度可以通过物资运抵总量与机场物资需求量的比值进行衡量，即为其中i，j∈τs，I=0，1，…，l。

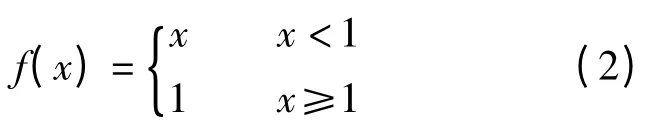
则有：

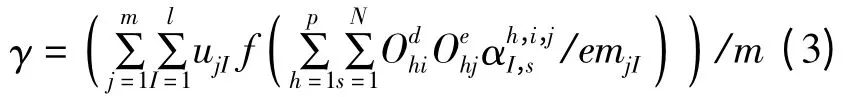
γ 反映不同物资需求紧要度约束下的物资需求满足程度。γ =0 表示所有机场的物资需求均不被满足，救灾效果满意度最低;γ =1 表示所有机场的物资需求均被满足，救灾效果满意度最高。

民航应急物资调度受到时间、物资储备数量和飞机性能的约束。一般认为，灾害发生后3 天内为黄金救援时间，因此要求调度方案的完成时间Tφ不能大于72 h。救灾点的物资储备量是有限的，从每个救灾点运出的应急物资总量不得超过救灾点的储备总量。同时，受制于飞机的运载能力，飞机每次运载的物资总量不得大于飞机的额定载运量。考虑飞机的有限航程，飞机h的调度任务序列φh中单次飞行的最远航线距离定为max{rφh}，则应有max{rφh}≤Rh。

应急调度有如下两个决策目标：

(1)要求应急调度方案的执行总时间最短，即F1=min { max{Th}}(h=1，2，…，p);

(2)要求应急调度方案的救灾效果最好，即F2=max{ γ} 。

为方便建立单目标数学模型，将F2变形为F2=min {1 -γ }。由此建立如下数学模型：

式(4)中，ω1，ω2分别为决策因子z1和z2的权重系数，设计如下权重系数：

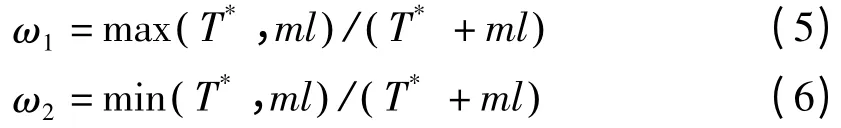
为确保决策因子受权重系数的约束，对决策因子进行归一化处理，得到单目标函数：

其中，T*=72，表示运输时间上限。

2 民航应急调度优化算法

2.1 算法流程

常用的元胞状态演化只与邻域内元胞的生死状态有关，而与个体适应度无关，这极有可能导致优秀个体的迅速消亡，从而降低算法的寻优能力。基于适者生存的生态法则，提出一种基于个体适应度的元胞状态演化规则，算法流程如图1 所示。

图1 算法流程图

2.2 遗传编码

将所有飞机的调度任务序列组成一条染色体。每架飞机的飞行任务序列组成一个基因片段，每个基因片段中的单次飞行任务为一个基因单元，每个基因单元中的救灾机场、物资运输量和受灾机场统称为基因位点。例如，现有救灾机场d1，d2，d3，受灾机场e1，e2和应急物资c1，c2，c3。则飞机h对应的染色体基因片段编码格式可以为表示飞机h从救灾机场d1出发前往受灾机场e2，运载的3 类应急物资数量分别为之后返回救灾机场d2，再运载物资前往受灾机场e1，运载的物资数量分别为直至任务结束。由此，整个应急调度方案可用如下编码表示：

其中，“||”将每架飞机的基因片段分隔开。

2.3 元胞空间初始化

初始元胞群体应随机选取，元胞空间不能太大，否则影响算法收敛速度;但也不能太小，否则可能引起早熟现象。为提高算法效率，应在种群生成时对染色体进行可行性验证，检验染色体是否满足约束条件。种群初始化后，将个体依次放置在元胞网格内，并随机确定元胞的生死状态。

2.4 元胞遗传操作

(1)选择。依次选择生存元胞作为中心元胞，并在邻域内选取适应度最大的生存元胞进行交叉和变异操作，得到新元胞的适应度，若其优于中心元胞适应度，则替代中心元胞，否则被舍弃。

(2)交叉。在双亲确定后，按照交叉概率pcross给每个基因片段分别选取一个交叉随机位，对换父代染色体和母代染色体中的每个基因片段上对应随机位点之后的基因单元，形成两个子代。例如，父代染色体为：

母代染色体为：

设定第一个基因片段的交叉随机位为2，第二个基因片段的交叉随机位为1，则交叉生成的两条子代染色体分别为：

子代染色体1：

子代染色体2：

对生成的子代染色体进行验证，如果满足验证要求，则进行后续操作;否则，将其舍弃，重新执行交叉操作。

(3)变异。生成子代染色体后，按照变异概率pmutate给每个基因片段分别选取一个变异随机位，将每个基因片段上变异随机位对应的基因位点数值突变为另一组数值，生成新的子代染色体。如果子代满足验证要求，则加入下一代种群;否则，将其舍弃，重新执行变异操作。

2.5 元胞状态演化

针对完整元胞遗传算法忽视个体适应度，降低了算法寻优能力的缺陷，笔者基于适者生存法则对元胞状态演化规则进行了改进。自然界中，个体存活取决于所处的生态环境和自身生存能力。生态环境越好，个体越容易存活;生存能力越强，个体也越容易存活。在元胞遗传算法中，生态环境可以通过生存元胞和死亡元胞的数量关系进行衡量。生存元胞越多，表明生态环境越好;反之，表明生态环境越差。同理，适应度越优，生存能力越强;适应度越差，生存能力越弱。将邻域空间(包含中心元胞)视为中心元胞的生存环境，将环境中的元胞分为生存(S=1 )和死亡(S=0 )两个群体，并设定如下状态演化规则：

当元胞(i，j)在t时刻状态为生存，即1 时，其在t+1 时刻的状态及概率为：

当元胞(i，j)在t时刻状态为死亡，即0 时，其在t+1 时刻的状态及概率为：

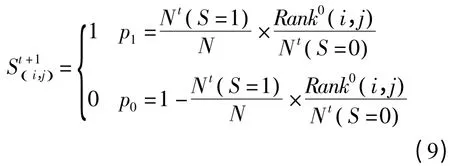
式中：S=1 或S=0 表示元胞处于生存或死亡状态;N为元胞个体生存环境中的元胞数量;Nt(S=1 )与Nt(S=0 )分别表示个体生存环境中状态为生存与死亡的元胞数量;Rank1(i，j) 为元胞(i，j) 的适应度在生存群体中的排名;Rank0(i，j) 为其在死亡群体中的排名，适应度从差到优进行排列。

2.6 控制参数及终止条件

元胞遗传算法的控制参数主要有邻域类型、种群规模ps、交叉概率pcross、变异概率pmutate和终止代数等。选定的邻域类型为Moore 类型，其模型包括中心元胞及周围8 个邻居元胞;群体规模ps=100，元胞空间大小为10×10;交叉概率pcross=0.9，变异概率pmutate=0.05。算法终止条件设为满足两个中的任意一个即可：①若迭代次数达到设定的最大值4 000;②若某代染色体的平均适应度达到这一代最佳染色体适应度的0.96。

3 实验结果及分析

3.1 初始条件设定

现有P1，P2，P3这3 种机型共7 架飞机从救灾机场d1，d2，d3运输药品、食品、生活用品3 种应急物资前往受灾机场e1，e2。已知机场d1无法保障P2机型，机场e2无法保障P1机型;救灾机场与受灾机场之间的航线距离如表1 所示。

表1 救灾机场与受灾机场航线距离 km

救灾机场的物资储备和受灾机场的物资需求如表2 所示;机型参数如表3 所示。

表2 物资储备和物资需求表 单元

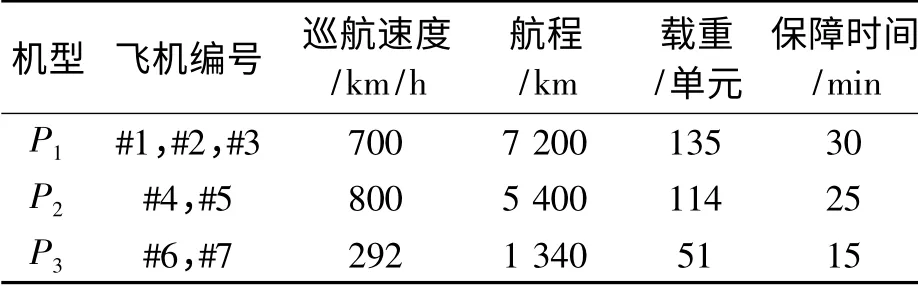
表3 机型参数表

3.2 调度方案分析

结合应急调度原理和数学模型的决策目标，将调度方案执行总时间和救灾效果满意度作为调度方案可行性评价参数。执行改进元胞遗传算法，迭代4 000 次得到最满意调度方案，如表4 所示。

表4 改进元胞遗传算法求解的最满意调度方案

该方案要求各架飞机执行任务的次数分别为9，9，8，11，11，6，7，运输效率较高的大机型P1和P2的任务次数较多，运输效率最低的小机型P3的任务次数最少。一般而言，机型越大，载重越大，速度越快，运输效率越高。因此，大机型被调用的优先级别高于小机型。受机场保障能力的限制，3 架P1型飞机#1，#2 和#3 只能前往受灾机场e1;两架P2型飞机#4，#5 只能在救灾机场d2和d3装载物资。受机型航程的限制，两架P3型飞机#6，#7 只能从救灾机场d2装载物资前往受灾机场e1，e2。执行该方案后各机场的物资量变动情况如表5 所示。

对比表2 和表5 可知，该方案的救灾效果满意度指数为1，各个受灾机场的物资需求均被满足，救灾效果达到最佳。最满意方案的执行总时间为52.551 h，明显低于72 h。实验结果表明，该数学模型合理可行。

表5 最满意方案下各机场的物资变动表 单元

3.3 不同算法下的方案求解及对比分析

将标准遗传算法(SGA)、完整元胞遗传算法(CEGA)和改进元胞遗传算法(MCGA)分别用于求解该算例。每个算法执行100 次，每次迭代4 000次并生成一组调度方案，每个算法均生成100 组调度方案。引入最满意函数值、整体平均值和函数值均方差作为执行一次算法的性能指标。对执行100 次算法的性能指标结果取平均值，得到如表6 所示的性能指标平均值对比表。

表6 3 种算法的性能指标平均值对比表

对100 组调度方案的最满意函数值取平均值，得到3 种算法的最满意函数值的平均值分别为0.787，0.746 和0.675，MCGA 算法搜寻出的最满意函数值明显优于SGA 和CEGA 算法。对100组调度方案中的所有迭代结果取平均值，得到3种算法的整体平均值分别为0. 815，0. 772 和0.698，说明MCGA 算法的寻优效率明显增强。前两组数据表明CEGA 和MCGA 在寻优能力和整体求解精度上较SGA 均有较大提高，而MCGA比CEGA 更胜一筹。对100 组调度方案得到的函数值均方差取平均值，得到均方差平均值分别为0.033，0.042 和0.037，说明MCGA 在进化收敛性上也比CEGA 略胜一筹。

4 结论

结合民航应急物资调度的特点，针对多机场民航应急物资联合调度问题，建立了以飞机性能和物资需求为约束，以运输时间最短、救灾效果最好为决策目标的数学模型。求解过程中提出一种改进元胞遗传算法，针对传统元胞遗传算法寻优能力不足的缺点，基于生态法则对元胞状态演化规则进行改进;最后设置算例进行求解。算例的最满意调度方案用时较短且取得了最佳的救灾效果，结果表明运输效率较高的大机型应优先调用，算例结果与实际情况相符，证明数学模型合理可行。对比标准遗传算法和完整元胞遗传算法，改进元胞遗传算法在寻优能力和收敛性两方面均有明显优势。

［1］ BERKOUNE D，RENAUD J，REKIK M，et al. Transportation in disaster response operations［J］. Socio -Economic Planning Sciences，2012，46(1)：23 -32.

［2］ LIU N，YE Y.Humanitarian logistics planning for natural disaster response with Bayesian information updates［J］. Journal of Industrial and Management Optimization，2013，10(3)：665 -689.

［3］ BOZORGI -AMIRI A，JABALAMELI M S，AL -E -HASHEM S M J. A multi -objective robust stochastic programming model for disaster relief logistics under uncertainty［J］.OR Spectrum，2013，35(4)：905-933.

［4］ SHEU J B.Dynamic relief-demand management for emergency logistics operations under large-scale disasters［J］. Transportation Research Part E：Logistics and Transportation Review，2010，46(1)：1 -17.

［5］ 文仁强，钟少波，袁宏永，等.应急资源多目标优化调度模型与多蚁群优化算法研究［J］. 计算机研究与发展，2013，50(7)：1464 -1472.

［6］ 王剑，王红卫.多目标资源受限的运输调度问题研究［J］.武汉理工大学学报，2008，30(5)：155- 158.

［7］ 梁勤欧.基于改进免疫算法的有能力约束车辆路径问题［J］. 武汉理工大学学报(信息与管理工程版)，2011，33(5)：763 -767.

［8］ 高鸿鹤，唐辰. 基于配送时间最短的应急物流路径规划［J］.物流工程与管理，2014，36(2)：75 -78.

［9］ OZDAMAR L. Planning helicopter logistics in disaster relief［J］.OR Spectrum，2011，33(3)：655 -672.

［10］ 祁明亮，秦凯杰，赵琰.雪灾救援物资车辆-直升机联合运送的调度问题研究［J］.中国管理科学，2014，22(3)：59 -67.

［11］ 黎明，王莹，陈昊，等.基于捕食机制的元胞遗传算法［J］.应用科学学报，2012，30(6)：669 -676.

［12］ KORNYAK V V. Symmetric cellular automata［J］.Programming and Computer Software，2007，33(2)：87 -93.