基于CCM+汽车排气消音器的分析与优化

袁守利，齐芸禾，黄 灿

(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉430070;2.武汉大学 物理科学与技术学院，湖北 武汉430072)

汽车排气消音器包括主消音器和副消音器，其主要功用是降低排气噪声。一般来说，排气背压越大，降噪效果越好，但降噪的同时，气阻的作用会导致排气不佳，使发动机功率降低，动力性衰减，促使降噪效果与背压形成一对矛盾体。因此应将噪声控制在一定值，通过对结构的优化，使背压值达到最小，这样既满足噪声的控制又满足动力性的要求，达到优化的目的［1-2］。

1 流场基本控制方程

由于催化器和副消音器背压阻力较主消音器小得多，故可将流场视为气体属性等同于主消音器内气体的常密度模型，其他模型选用三维、定常、粘性、湍流运动，其控制方程包括连续性方程、动量方程、能量方程、湍流动能方程和湍流耗散方程。

流体流动受物理守恒定律的支配，基本的守恒定律包括能量守恒定律、质量守恒定律和动量守恒定律，分别用能量守恒方程、质量守恒方程和动量守恒方程表示。如果流动处于湍流状态，系统还应遵守附加的湍流输运方程［3］。

1.1 质量守恒方程

根据质量守恒定律，单位时间内流体微元体中质量的增加等于同一时间间隔内流入该微元体的静质量。

由于选用常密度气体，密度不随时间变化，故方程变为：

式中：ρ 为密度;t为时间;u、v、w为速度矢量在x、y、z这3 个方向的分量。

1.2 动量守恒方程

动量守恒定律的物理意义是指微元中流体的动量变化率等于作用在该微元上各种外力之和。按照这一定律，可导出x、y、z3 个方向的动量守恒方程。

式中：μ 为动力粘度;Su、Sv、Sw为动量方程的广义源项。

1.3 能量守恒方程

能量守恒定律是包含有热交换的流动系统必须满足的基本定律，该定律可表述为：微元体中能量的增加率等于进入微元体的净热流量加上体力与面力对微元体所做的功。

以温度T为变量的能量方程为：

式中：cp为比热容;T为温度;k为流体传热系数;ST为流体的内热源及由于粘性作用而使流体机械能转化为热能的部分。

确定控制方程后，还需确定计算相关的初始条件，联立方程才可以计算。在此，初始条件设置参考出口边界条件，通过一个周期的计算，可以得到一个初始的压力场及速度场，再经过第二个周期的计算，压力和速度慢慢得以修正至最新值。

2 几何模型建立及网格划分

排气系统结构、副消音器结构、主消音器结构如图1 ～图3 所示。将原三维模型导入Hypermesh 中，利用Hypermesh 几何模块抽取模型的内表面作为流体域，封住进出口形成拓扑封闭的空间域后，导入STAR -CCM +，利用其进行面网格及体网格的划分。面网格采用三角网格，体网格采用多面体网格，并对腔内小孔周围进行局部加密。基本尺寸为8 mm，体网格数量为190万个。

图1 排气系统结构图

图2 副消音器结构图

图3 主消音器结构图

3 边界条件

分析选用常密度气体模型，由于整个系统背压阻力主要集中在主消音器，为使误差降到最低，故选用接近主消音器内部温度(900 K)对应的气体属性［4］，900 K 时的排放气体属性参数如表1所示，该数据来自GT -power 中的计算结果。由发动机的标定试验得出入口条件如表2 所示。

表1 900 K 时主消音器内部气体属性

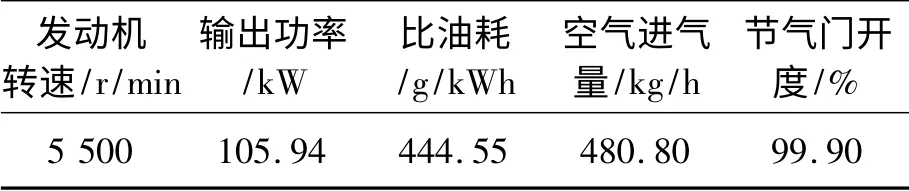
表2 5 500 r/min 时发动机输出特性

经计算得出入口质量流量为0.146 kg/s。

边界条件设置如下：

(1)入口边界条件。入口选用质量流量边界条件，质量流量为0. 146 kg/s，入口温度为1 011 K。

(2)出口边界条件。出口选用压力边界条件，出口相对压力为0 Pa，出口温度为733 K。

(3)壁面选用无滑移边界，粗糙度为0.5 mm，环境温度为300 K，对流换热系数为75 W/(m2·K)，催化器壁面设为绝热。

(4)初始条件。温度设为733 K，绝对压力为0 Pa;催化器采用多孔介质表示，其惯性阻力系数为100 kg/m4;粘性阻力系数为1 500 kg/(m3·s)。

4 计算结果与分析

4.1 压力分布

4.1.1 排气系统压力分布

排气系统压力云图如图4 所示，可以看出入口压力为最大值，总压力达到47.5 kPa。从入口到出口，压力逐渐递减，在主消音器位置压降尤为明显，其主要原因是从管流入腔截面积突然增大及主消音器内部带孔隔板节流作用，使原流体流动受到极大干扰和冲击，引起扩缩损失［5］。消音器的压力损失越大，产生的背压越大，排气系统的排气效率越低，使发动机的做功效率降低，从而影响发动机的动力性和燃油经济性［6］。

图4 排气系统压力云图

4.1.2 副消音器压力分布

副消音器压力云图如图5 所示。副消音器管路中压力明显大于膨胀腔压力，并沿管路递减。副消音器压力损失为1 kPa。

图5 副消音器压力云图

4.1.3 主消音器压力分布

主消音器压力云图如图6 所示。主消音器最大压力出现在进气管入口处，沿着管路压力逐渐减小，主消音器整体压力损失为29 kPa，主要集中在三、四、五腔，气流顺着五腔、四腔、三腔依次递减，各腔压力分布均匀。

图6 主消音器压力云图

4.2 速度分布

4.2.1 排气系统速度分布

排气系统速度云图如图7 所示。入口流速为119 m/s，气流从入口到副消音器出口，速度基本保持不变，再经中间管路，速度明显增加。在管路拐点处，其速度大于其他地方，这是因为管路截面的平均流速相等，但是由于弯管曲率过大，使截面内速度不均匀，造成局部流速过大。

图7 排气系统速度云图

4.2.2 副消音器速度

副消音器速度云图如图8 所示。从图8 可以看出，管路中速度明显大于各腔内速度，气流只在膨胀腔内稍有扩散，一、三腔内气流速度基本为0，可见副消音器对系统背压影响很小。

4.2.3 主消音器速度

主消音器速度云图如图9 所示。主消音器内气流速度最大值出现在连通管入口，这是因为截面积突然变小，使速度急剧增加。在连通管末端气流由于惯性产生射流，冲击第五腔壁面。射流内部压强低于周围静止气体的压强，射流周围气体被卷吸进入射流，因此射流体积逐渐增大，速度逐渐降低。气流经过带孔隔板，也会产生射流，因为截面积突然变小，速度明显增加，从图9 可以看出隔板小孔处速度梯度较大。

图8 副消音器速度云图

图9 主消音器速度云图

4.3 温度分布

4.3.1 排气系统温度分布

排气系统温度云图如图10 所示。由图10 可以看出，催化器内温度高于两端管路，催化器入口温度为993 K，由于催化器内部的摩擦作用，使催化器出口温度升高为1 001 K。在催化器之后，管路中温度明显高于腔内温度，而温度随着气流方向逐渐降低［7］。

图10 排气系统温度云图

4.3.2 副消音器温度

副消音器温度云图如图11 所示。在副消音器第二腔由于膨胀腔作用，气体在腔内扩散，温度逐渐降低，而一、三腔由于仅有较少气体流入，故温度都较低。

4.3.3 主消音器温度

主消音器温度云图如图12 所示。主消音器温度最大值出现在进气管入口处，由于第二腔截面变化使气体扩散，连通管中温度逐渐降低。在连通管出口处，局部温度过高。气流流经带孔隔板后，温度分布均匀。

图11 副消音器温度云图

图12 主消音器温度云图

4.4 速度流线图

副消音器速度流线图如图13 所示。由图13可以看出气体在膨胀腔产生湍流，由于流速较低，湍动并不剧烈。而一、三腔气体流入较少，由此可以解释上述一、三腔温度和压力较低的原因［8］。

图13 副消音器速度流线图

主消音器速度流线图如图14 所示。主消音器湍流主要出现在三、四、五腔，在连通管末端速度最大，湍流也最剧烈，因此造成压力损失也最大。而三、四、五腔由于两个带孔隔板的作用，气流穿过小孔产生的射流也是消耗湍动能的主要原因［9］。

图14 主消音器速度流线图

4.5 优化方案

(1)建议在四、五腔隔板上增加打孔数量，孔数由原来的144 个增加至160 个，孔径不变。

(2)缩短排气管插入第三腔长度至10 mm，使排气更流畅。

5 改进前后结果对比

5.1 CFD 分析

改进后主消音器压力云图如图15 所示，整体背压由46.5 kPa 降至41.7 kPa，主消音器背压由29 kPa 降至24.5 kPa，与改进前主消音器压力云图相比，进气管入口压力明显降低，差值为4.5 kPa。

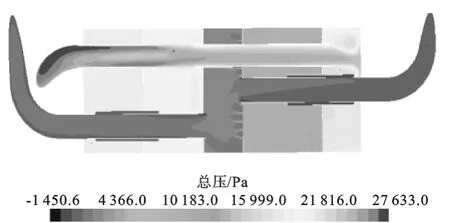
图15 主消音器压力云图

5.2 GT-power 分析

基于GT-power 对改进前后的背压及噪声曲线对比分析，图16 为转速-压力曲线对比图，图17 为转速- 噪声曲线对比图。由图16 和图17可以看出，改进后背压在最高转速时下降了4 kPa，与CFD 分析结果基本一致，而怠速噪声只增长了0.5 dB，最高转速对应噪声基本不变。综合而言，优化方案达到了预期效果，使背压降到理想区域内，对排气系统起到了改善作用［10-11］。

图16 背压对比曲线

图17 噪声对比曲线

6 结论

笔者通过对某1.5 T SUV 排气消音器的分析及优化，在保证降噪效果的前提下达到了减小背压的目的。说明利用数值分析的方法可以缩短开发周期，减少大量重复性试验工作，节约成本，使排气消音器设计更加合理。

［1］ ASHOK P，SHIVDAYAL P，UMASHANKER G. Commercial vehicles muffler volume optimization using CFD simulation［J］.SAE International，2014(9)：2-4.

［2］ HOCHEOL S，SEJONG P，KYOUNGSUK P.Numerical study on the flow noise generation in an automotive muffler system［J］.SAE International，2007(8)：1 -6.

［3］ 王福军.计算流体动力学分析［M］.北京：清华大学出版社，2004：36 -54.

［4］ 郭学敏.乘用车排气系统冷端内流场仿真及消声器再生噪声预测［D］.武汉：武汉理工大学，2011.

［5］ 王计广.基于Fluent 的汽车消音器压力场及温度场数值分析［J］.汽车工程师，2011(6)：30 -32.

［6］ 许建民.汽车消音器的流场和压力损失分析［J］.武汉科技大学学报，2011(1)：69 -71.

［7］ 金雪.乘用车排气系统流场的数值模拟［D］.武汉：武汉理工大学，2010.

［8］ 李洪亮，王海洋，王务林.汽车排气系统的流场分析与优化［J］.汽车技术，2010(1)：15 -16.

［9］ 王少康. 消声器内三维流动的数值模拟研究［D］.长春：吉林大学，2007.

［10］ 毕嵘. 汽车进排气消声器性能的数值仿真研究［D］.合肥：合肥工业大学，2007.

［11］ 刘伯潭，潘书杰.某车型排气系统总成的CFD 模拟研究［C］// 2008 中国汽车工程学会年会. 天津：［s.n.］，2008：34 -36.