基于PSODACCIW-VPMCD的滚动轴承智能检测方法
刘吉彪,程军圣,马利
(1.河南工业职业技术学院机械工程系,河南南阳473000;2.湖南大学机械与运载工程学院,长沙410082)
基于PSODACCIW-VPMCD的滚动轴承智能检测方法
刘吉彪1,程军圣2,马利2
(1.河南工业职业技术学院机械工程系,河南南阳473000;2.湖南大学机械与运载工程学院,长沙410082)
针对VPMCD中模型选择方法的不合理和小样本多分类时识别率降低的缺陷,结合动态加速常数协同惯性权重的粒子群(Particle swarm optimization with dynamic accelerating constantand coordinatingwith inertiaweight,PSODACCIW)算法的全局优化能力和加权融合理论,提出基于PSODACCIW-VPMCD的滚动轴承智能检测方法。首先对样本提取特征变量,然后采用PSODACCIW算法优化诊断融合权值矩阵,最后对滚动轴承的故障类型和工作状态进行分类和识别。实验结果表明,该方法能够有效地应用于滚动轴承的智能检测中。
动态加速常数协同惯性权重的粒子群算法(PSODACCIW);基于变量预测模型的模式识别(VPMCD);加权融合;滚动轴承;智能检测
对滚动轴承进行故障诊断,其本质上可以归结为对滚动轴承振动信号的模式识别过程[1]。目前应用较为广泛的有支持向量机、神经网络等,但这些方法都存在一定的局限性[2-3]。特别是这两种分类器都忽略了从原始数据中提取的全部或部分特征值之间的相互内在关系,另外,当故障类型和工作状态不同时,其相互内在关系有明显的不同。因此,Raghuraj与Lakshminarayanan提出一种新的模式识别法——基于多变量预测模型的模式识别(Variable Predictive Mode based Class Discriminate,VPMCD)法。该方法首先充分利用从原始数据中提取的全部或部分特征值之间的相互内在关系来建立数学模型,然后采用已知样本数据对模型参数进行估计,得到不同类型的预测模型,最后采用预测模型对测试样本进行分类[4-5]。
在VPMCD法中,如何选择变量预测模型成为模式识别过程中的关键问题。原方法以误差平方和最小为依据选择模型类型和对应阶数,使得在模型选择上存在绝对化而导致VPMCD法缺乏适应性,且计算量较大。另外,在模型参数的估计方面有待进一步提高,尤其是在小样本多分类情况下,VPMCD法由于缺乏大量的试验样本导致预测变量数目较少,变量间的线性相关性也相应降低,估计所得的模型拟合性变差,这样可能降低估计精度。因此,VPMCD法的应用存在一定的局限性,在实际应用中则是表现为识别精度低[6]。
为了将VPMCD法引入小样本多分类滚动轴承故障智能检测中,针对VPMCD法模型选择的问题,可以采用常见的智能优化算法对参数进行优化。遗传算法虽然具有简易快速和容错性强等特点,但是其自身仍然存在缺陷,如早熟收敛易陷入局部最优解,局部搜索能力不足导致无法收敛至全局最优解和无方向性降低遗传算法的进化速度等。鉴于遗传算法在系统优化方面的不足,提出了基于PSODACCIW-VPMCD(Variable predictive model based class discriminate and Particle swarm optimization with dynamic accelerating constant and coordinating with inertia weight,PSODACCIW-VPMCD)故障诊断法[7-8]。在PSODACCIW算法中,首先对粒子随机赋值,然后迭代更新寻找优化问题的最优解。优化问题的潜在解存在于搜索空间的所有粒子中,并且每个粒子均有由被优化函数确定的适应度值,然后粒子追随当前最优粒子在空间中进行搜索,最终寻找到最优解。PSODACCIW算法实现了惯性权重和动态加速常数随迭代次数的变化而变化,优化网络的收敛速度加快而不易陷入局部极值从而具有更高的全局搜索效率,因此在复杂系统优化方面具有较强的鲁棒搜索能力。鉴于此,将PSODACCIW算法用于优化VPMCD法,并应用于滚动轴承的故障智能检测中。
在使用PSODACCIW-VPMCD法进行故障诊断时,首先分别选择四种模型:线性模型、二次模型、交互模型、二次交互模型和不同的阶数进行组合对样本进行训练,相应地得到不同的弱变量预测模型,通过PSODACCIW算法的全局优化能力对建立的弱变量预测模型的权值进行优化,得到若干个弱变量预测模型的最优权值矩阵;接着在模型测试阶段,通过模型训练阶段建立的弱变量预测模型对测试样本进行预测,得到测试样本的预测值;然后利用加权融合思想,对最优权值矩阵和测试样本的预测值进行加权,得到测试样本的最优预测值;最后以同一类别下所有特征值的最优预测值和真实值的误差平方和最小为判别依据对测试样本进行分类[9-10]。
1 PSODACCIW算法
为了在优化前期使粒子遍历整个搜索空间,在优化后期提高趋于最优解的收敛率并有效地找到最优解,首先初始化PSODACCIW算法的参数,参数初始化数据见表1,使加速因子w随进化代数线性改变,惯性权值w随进化代数线性递减,粒子的速度V=[vi1,vi2,vi3,…,vid]和位置X=[xi1,xi2,xi3,…,xid]定义成在(0,1)之间的随机数。

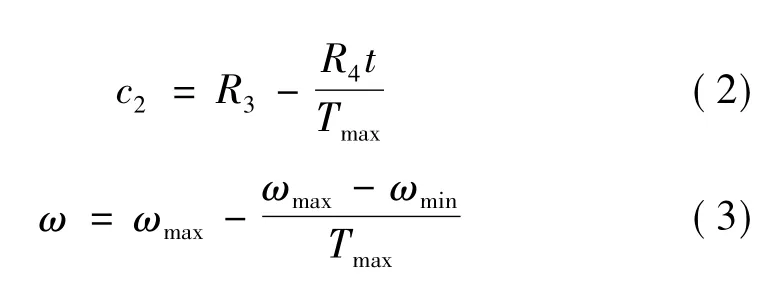
式中:自适应控制常数R1,R2,R3,R4是初始的定值;t,Tmax分别是当前迭代代数和最大迭代数,wmax和wmin分别是最大权重和最小权重。
其次在VPMCD中以测试样本的预测值和真实值的最小误差平方和最小为依据来对样本进行智能检测,因此在PSODACCIW算法中,以测试样本预测值和真实值误差的范数作为适应值,目标是最小化适应值,也就是使预测值和真实值的误差的范数达到最小值来实现对滚动轴承样本故障的分类。然后根据式(1)~式(5)对粒子的位置和速度进行迭代更新,直到找到搜索空间中的最优解。
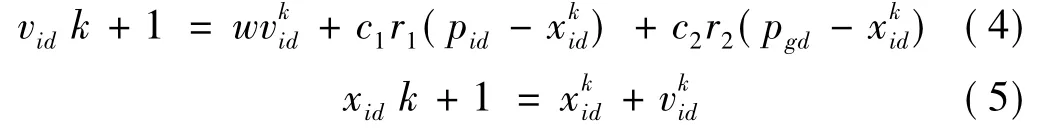
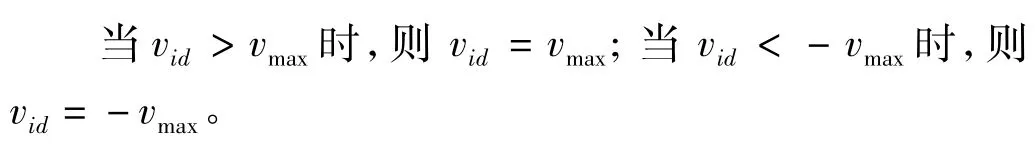
式中:r1和r2为服从[0,1]均布的随机数;和分别为第k次迭代第i个粒子速度矢量和位置矢量的第d维分量;pid和pgd分别为每个粒子的历史最优位置和所有粒子中的全局最优位置[11]。
2 PSODACCIW-VPMCD基本原理
首先由于PSODACCIW-VPMCD法避免了VPMCD法在采用最小二乘回归估计模型参数时存在的缺陷,即样本较少时模型回归拟合精度降低,从而PSODACCIW-VPMCD法能够适用于小样本多分类的滚动轴承故障智能检测;其次,PSODACCIW-VPMCD法避免了VPMCD法中模型选择方法不合理这一问题,通过模型的不同类型和不同阶数的组合对滚动轴承的故障类型和工作状态进行分类;然后,基于PSODACCIW算法的全局优化能力,对若干个弱VPM的权值进行优化得到的最优权值矩阵能够反映不同类型和阶数的模型对样本分类结果的贡献量,识别精度有了进一步的提高;最后采用加权融合的思想,用最优权值矩阵对测试样本的预测值进行加权从而得到测试样本的最优预测值,在一定程度上提高了预测模型的分类效果和识别精度。
在滚动轴承的故障智能检测中,通常采用特征向量[X2,X3,…,Xp],p表示特征值的个数来描述故障类别,由于提取的全部或部分特征值之间具有某种内在的变量关系,因此在不同的故障类别中,其他特征值[X2,X3,…,Xp]的变化会导致X1随之改变,而X1随其他特征值改变的关系有一对一的线性或者非线性关系X1=f(X2)或者一对多的关系X1=f(X2,X3,…)。为了识别系统故障,需要建立数学模型,特征值Xi定义的变量预测模型VPMi为一个线性或者非线性的回归模型,主要有四种数学模型:线性模型(L),二次模型(Q),线性交互模型(LI),二次交互模型(QI),以p个特征值为例,对四种数学模型中任意一个模型采用特征值Xj(j≠i)对Xi进行预测,得到:
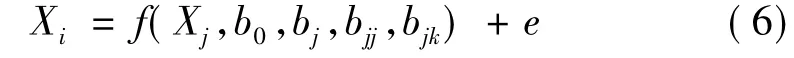
式(6)称为特征值Xi的变量预测模型VPMi,又称为弱变量预测模型。
其中:特征值Xi为被预测变量;Xj(j≠i)为预测变量;b0、bj、bjj和bjk为模型参数;e为预测误差,其中r≤p-1为模型阶数。
由于采用VPMCD法选择的最优变量预测模型存在绝对性,所以建立的预测模型只能在一定程度上反映特征变量之间的相互内在关系。因此,为了能够全面地反映特征变量之间的相互内在关系,提出了基于加权融合思想的PSODACCIW-VPMCD的滚动轴承故障智能检测方法。
2.1 PSODACCIW-VPMCD模型的训练
⑴对g类故障分类问题,收集n个训练样本,取每一类故障样本数为n1,n2,…,ng。
⑵提取所有的训练样本特征值X=[X1,X2,…,Xp]。
⑶对任意特征值Xi,选择模型类别、模型阶数以及预测变量。
在模型训练阶段,分别选取线性模型(L),二次模型(Q),线性交互模型(LI),二次交互模型(QI)之一和模型阶数r(r=1,2,3,…,p-1)组合。
⑷令k=1,对nk个第k类训练样本中的任意一个样本,对每一个特征值Xi建立其数学模型,所以对每一个特征值Xi都可以建立nk个数学方程,得到式(6)所示的特征值Xi的变量预测模型VP。
⑸令k=k+1,循环步骤⑷,直至k=g时结束。
2.2 PSODACCIW-VPMCD模型的分类
(1)选择测试样本后提取其特征值X=[X1,X2,…,Xp]。
(2)对测试样本的所有特征值Xi,i=1,2,…,p,分别采用在模型训练阶段得到的N个变量预测模型VPM对其预测,得到预测值表示第k类、第n个弱变量预测模型对第i个特征变量的预测值。
(3)采用动态加速常数协同惯性权重的粒子群优化算法(PSODACCIW)优化N个弱变量预测模型的权值,得到表示第n个弱变量预测模型对第k类,第i个特征变量优化的权值。

3 基于PSODACCIW-VPMCD的滚动轴承智能检测法
由于拾取的滚动轴承振动信号表现出非线性和非稳定性,因此采用局部特征尺度分解(Local characteristic scale decomposition,LCD)法进行信号处理,LCD能够将复杂信号分解成若干个瞬时频率具有物理意义的内禀尺度分量(Intrinsic scale component,ISC)之和。对振动信号进行信号处理过后,接着就要提取信号特征,根据矩阵论,奇异值是矩阵的固有特征,并且具有良好的稳定性,同时矩阵奇异值具有比例不变性和旋转不变性。因此,矩阵奇异值符合在模式识别中特征提取时所要满足的稳定性及比例、旋转不变性的要求,从而能够有效地描述初始特征向量的特征[12-13]。
基于PSODACCIW-VPMCD的滚动轴承智能检测法的步骤如下:
步骤1以采样率fs在一定转速下对滚动轴承正常、内圈故障、外圈故障三种状态进行采样,每种状态采集N个样本;
步骤2采用LCD法对振动原始信号进行分解,得到若干个内禀模态函数(ISC)分量。
步骤3提取前i个包含主要故障信息的ISC分量并进行奇异值分解,得到奇异值矩阵作为特征向量,每种状态下得到N×i阶的特征值矩阵。
步骤4每种状态取n个样本作为训练样本,将特征向量输入到不同模型类型和不同阶数组合的VPMCD分类器中对其进行训练,对所有故障状态下的所有特征值建立N个变量预测模型VP,其中k=1,2,…,g代表不同类别,i=1,2,…,p代表不同的特征值。
步骤5采用动态加速常数协同惯性权重的粒子群优化算法(PSODACCIW)优化弱变量预测模型的最优权值矩阵。
步骤6将剩下的样本作为测试样本,用训练好的N个预测模型对测试样本进行预测,将得到的预测值与⑸中最优权值矩阵Wik加权融合。
步骤7以最小误差平方和为依据,根据PSODACCIW-VPMCD分类器的输出结果来确定滚动轴承的工作状态和故障类型。
4 实验分析
滚动轴承在长期运行过程中通常会出现内圈故障,外圈故障和滚动体故障。为了验证改进VPMCD法的有效性,采用湖南大学现场实际数据,通过激光切割法分别在滚动轴承的内圈和外圈上开槽来模拟内圈故障和外圈故障,滚动轴承故障实验参数(见表1和表2)。由于实验条件的限制而未能在滚动体上设置故障。图1和图2分别为滚动轴承故障实验室装置及其实物图,振动信号由轴承座上的加速度传感器采集,调速电机为直流伺服电机,功率为600 W,采集正常状态下15组、外圈故障状态下25组、内圈故障状态下20组样本。其外圈故障状态下的滚动轴承振动信号时域图和对应包络谱图(见图3和图4)。

表1 PSODACCIW算法参数初始化Tab.1 PSODACCIW algorithm Parameters initialization

表2 滚动轴承故障实验参数Tab.2 Rolling bearingfault experimental parameters
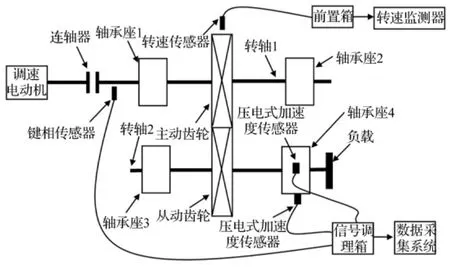
图1 滚动轴承故障实验装置Fig.1 Rolling bearing fault experiment device
将采集到的滚动轴承的振动信号经过LCD法分解得到从高到低不同频率段的单分量信号,由于滚动轴承故障振动信号的故障信息主要集中在高频段,所以选择前4个ISC分量组成矩阵,滚动轴承振动信号的前若干个包含主要故障特征信息的ISC分量构成的矩阵作为最初的矩阵,经过奇异值分解后得到的对角阵中的非负递减的奇异值构成的矩阵作为特征向量输入到PSODACCIW-VPMCD中进行模式识别。

图2 滚动轴承故障实验装置实物图Fig.2 Rolling bearing fault experiment device entity

图3 外圈故障状态下滚动轴承振动信号时域波形Fig.3 Rolling bearing vibration signalwaveform in time domain of the outer ring fault condition

图4 外圈故障状态下滚动轴承包络谱图Fig.4 Envelope spectral diagram of rolling bearing with outer ring fault
在小样本多分类的滚动轴承的故障智能诊断中,分别选取滚动轴承正常状态、外圈故障和内圈故障的振动信号15组,25组,20组数据,在正常样本和其余两类故障样本数据中各随机抽取7组数据作为训练样本数据,将剩下的8组,18组,13组数据作为测试样本代入变量预测模型中进行分类。首先采用VPMCD法,采用不同类型(L,LI,QI,Q)和阶数(r=1,2,3)的模型进行组合,从中选择r=3的线性模型(L)VPM(1,3),r=3的线性交互模型(LI)VPM(2,3),r=2的二次交互模型(QI)VPM(3,2)和的r=2二次模型(Q)VPM(4,2)这四种模型,然后对训练样本和测试样本采用随机抽样原则,模型诊断结果(见表3)。从表3可知,VPM (2,3)的识别率相较于其他三种模型最高,达到了82.06%,四种故障诊断模型的识别率有差异且识别精度不高,没有达到理想的诊断效果。
为了避免模型选择对识别精度的影响,采用PSODACCIW-VPMCD法对滚动轴承故障进行诊断和分类识别,分别采用r=3的线性模型VPM(1,3),r=3的线性交互模型VPM(2,3),r=2的二次交互模型VPM(3,2)和的r=2二次模型VPM(4,2)这四种模型对滚动轴承三种状态下小样本进行训练,得到每个特征值相应的四种弱变量预测模型,然后采用PSODACCIW算法对上述四种弱变量预测模型的权值进行优化,其中滚动轴承内圈故障状态下特征变量X4的四种弱变量预测模型和最优权值(见表4),再将测试样本的预测值和最优权值进行加权融合,最后得到测试样本的最优特征变量预测值,以测试样本的最优特征变量预测值和特征变量真实值的预测误差平方和值最小为判定依据进行分类识别,并且取得了较好的分类结果,为了进一步验证PSODACCIW-VPMCD法的优越性,采用遗传算法对四种弱变量预测模型的权值进行优化,其他实验过程保持不变,得到的基于GA-VPMCD的滚动轴承故障识别结果,两种改进VPMCD法的识别结果对比(见表5)。

表3 VPMCD法的滚动轴承故障识别率Tab.3 Fault identification accuracy rate based on VPMCD for rolling bearing

表4 滚动轴承内圈故障状态下特征变量的四种弱VPM的最优权值Tab4.The four weak VPM s and their weights of the rolling bearing vibration signal’s Feature variable w ith inner fault

表5 两种改进VPMCD的识别结果对比Tab.5 Recognition resu lt contrast of two kinds of im proved VPMCD
由表5可知,PSODACCIW-VPMCD比原VPMCD和GA-VPMCD法具有更好的分类效果和更高的识别率,虽然在正常状态下和外圈故障状态下的识别率相同,但是在内圈故障状态下的测试样本有2个未被正确识别,PSODACCIW-VPMCD法的综合识别率达到了97.44%,相比于表3中原VPMCD法的识别率有很大的提高。因此,PSODACCIW-VPMCD对滚动轴承故障的智能诊断具有明显的效果,实验结果证明了PSODACCIW-VPMCD法的有效性。
5 结论
针对原VPMCD法在模型选择方法的不合理和在小样本多分类条件下识别率降低的问题,提出了PSODACCIW算法优化的多变量预测模型(PSODACCIWVPMCD)的诊断法,将其应用于小样本多分类条件下的滚动轴承故障智能检测中,实验数据的分析结果表明了该方法的有效性,经分析得到如下结论:
(1)PSODACCIW-VPMCD法采用动态加速常数协同惯性权重的粒子群算法对弱变量预测模型的权值进行优化,并且将加权融合的思想引入到各种模型的预测结果中,避免了原VPMCD法在模型选择方法的不合理而导致其缺乏适应性。
(2)PSODACCIW-VPMCD法应用于小样本多分类的滚动轴承的故障诊断中,相较于原VPMCD法和GAVPMCD法,其诊断精度有很提高。
对滚动轴承的故障振动信号的分析结果表明,基于PSODACCIW-VPMCD的滚动轴承故障智能检测法可以准确、有效地对小样本多分类条件下的滚动轴承的工作状态和故障类型进行分类,从而为滚动轴承的故障诊断提供一种新的智能检测法。
[1]温熙森.模式识别与状态监控[M].北京:科学出版社,2007.
[2]Wang Hua-qing,Chen Peng.Intelligent diagnosismethod for rolling element bearing faults using possibility theory and neural network[J].Computer&Industrial Engineering,2011,60(4):511-518.
[3]Fei Sheng-wei,Zhang Xiao-bin.Fault diagnosis of power transformer based on support vector machine with genetic algorithm[J].Expert Systems with Applications,2009,36(8):11352-11357.
[4]Raghuraj R,Lakshminarayanan S.Variable predictive models:a new multivariate classification approach for pattern recognition applications[J].Pattern Recognition,2009,42(1):7-16.
[5]Raghuraj R,Lakshminarayanan S.Variable predictive model based classification algorithm for effective separation of protein structural classes[J].Computational Biology and Chemistry,2008,32(4):302-306.
[6]Wang Hua-qing,Chen Peng.Intelligent diagnosismethod for rolling element bearing faults using possibility theory and neural network[J].Computer&Industrial Engineering,2011,60(4):511-518.
[7]刘芬,潘宏侠.PSODACCIW优化的小波神经网络在传动箱故障诊断的应用[J].噪声与振动控制,2011,5:146-149.
LIU Fen,PAN Hong-xia.Study on application of PSODACCIW optimizing wavelet neural network for gear box fault diagnosis[J].Noise and Vibration Control,2011,5: 146-149.
[8]Bocaniala C D,Sa da Costa J L.Tuning the parameters of a classifier for fault diagnosis-particle swarm optimization vs genetic algorithms[J].ICINCO,2004(1):157-162.
[9]Eunju Kim,Wooju Kim,Yillbyung Lee.Combination of multiple classifiers for the customer's purchase behavior prediction[J].Decision Support Systems,2002,34:167-175.
[10]刘占生,窦唯,王东华.基于遗传算法的旋转机械故障诊断方法融合[J].机械工程学报,2007,43(10):227-233.
LIU Zhan-sheng,DOU Wei,WANG Dong-hua.Rotating machinery fault diagnosis combination of method based on genetic algorithm[J].Journal of Mechanical Engineering,2007,43(10):227-233.
[11]魏秀业,潘宏侠.粒子群优化及智能故障诊断[M].北京:国防工业出版社,2010.
[12]程军圣,郑近德,杨宇.一种新的非平稳信号分析方法——局部特征尺度分解法[J].振动工程学报,2012,25 (2):215-220.
CHENG Jun-sheng,ZHENG Jin-de,YANG Yu.A nonstationary signal analysis approach—the local characteristic-scale decomposition method[J].Journal of Vibration Engineering,2012,25(2):215-220.
[13]Jiang Yong-hua,Tang Bao-ping,QinYi,et al.Feature extraction method of wind turbine based on adaptive Morlet wavelet and SVD[J].Renewable Energy,2011,36(8): 2146-2153.
An intelligent detection method for rolling bearings based on PSODACCIW-VPMCD
LIU Ji-biao1,CHENG Jun-sheng2,MA Li2
(1.Department of Mechanical Engineering,Henan Polytechnic Institute,Nanyang 473000,China; 2.College of Mechanical and Vehicle Engineering,Hunan University,Changsha 410082,China)
Aiming at the unreasonablemodel selection method and the defect of lower recognition rate for smaller samples and multi-classification,combining the global optimization ability of the particle swarm optimization with dynamic accelerating constant and coordinating with inertia weight(PSODACCIW)algorithm and the weighted fusion theory,an intelligent detection method for rolling bearings based on PSODACCIW-VPMCD was put forward.Firstly,the characteristic variables of samples were extracted,then the PSODACCIW algorithm was used to optimize the diagnosis fusion weightingmatrix.Finally,the operation status and fault pattern of rolling bearings were classified and identified.The test results showed that the proposed method can be applied in o rolling bearing intelligent detection effectively.
particle swarm optimization with dynamic accelerating constant and coordinating with inertia weight (PSODACCIW);variable predictive model-based class discriminate(VPMCD);weighted fusion;rolling bearing; intelligent detection
TH165.3;TH132.41
A
10.13465/j.cnki.jvs.2015.23.008
国家自然科学基金(51175158,51075131);湖南省自然科学基金(11JJ2026)
2014-03-31修改稿收到日期:2014-11-06
刘吉彪男,硕士,副教授,1968年生

