一种基于WMUWD的液压泵振动信号预处理方法
孙 健,李洪儒,王卫国,许葆华
(军械工程学院,石家庄 050003)
一种基于WMUWD的液压泵振动信号预处理方法
孙 健,李洪儒,王卫国,许葆华
(军械工程学院,石家庄 050003)
针对轴向柱塞液压泵故障引起的振动信号非线性强、故障信息湮灭在噪声干扰的问题,提出一种基于加权形态非抽样小波分解(WMUWD)的振动信号预处理方法。首先,在形态非抽样小波分解的一般框架下,提出WMUWD方法,利用特征能量因子表征形态非抽样各分解层近似信号对故障特征的贡献量,并以此为依据进行加权融合,以提高有用信息比重,便于特征提取;在此基础上,对WMUWD方法的初始参数设置进行了分析,给出了一套比较系统的优选组合方法;最后,利用仿真信号以及液压泵实测振动信号验证了该方法的有效性。
信号预处理;形态非抽样小波分解;加权融合;液压泵
液压泵是液压系统的关键部件之一,其性能好坏直接影响着整个液压系统的可靠性。由于流体的压缩性、泵源与伺服系统的流固耦合作用以及自身所具有的大幅固有机械振动,液压泵在出现故障时振动信号呈现较强的非线性、非平稳性,传统的线性信号分析方法已不再适用[1]。因此,有必要寻求一种有效的液压泵振动信号预处理方法,以提高故障预测的准确度。
目前,常用的非线性信号处理方法主要有经验模态法[2](EMD)和小波分析法[3],但是EMD存在模态混叠现象,小波分析在重构过程中的采样操作,会导致部分信息的遗漏,而且对于基函数的选择也存在问题。为此,文献[4-5]提出了形态小波分解(Morphological Wavelet Decomposition,MWD)的概念,实现了大多数线性与非线性小波的统一,但是在信号逐层分解过程中会出现信息减半的问题,导致较高层信号信息量不足,影响了信号预处理效果;针对此问题,Zhang等[6]提出了一种形态非抽样小波分解方法(Morphological Undecimated Wavelet Decomposition,MUWD),省去了传统小波分解的下抽样和重构的上抽样,有效避免了因降噪引起的失真问题和信息遗漏问题,在振动信号处理方面取得了一定成果[7-8]。但是,通过分析MUWD算法的原理可知,其主要存在两方面问题:一方面,它是以信号最高分解层的近似信号作为预处理结果的,并未考虑其余分解层的近似信号,这样会导致部分故障信息的遗漏,影响特征提取的效果;另一方面,MUWD参数设置(分解层数以及结构元素长度的选择)大多是基于经验给出的,缺乏一套系统的优选方法,一定程度影响了信号预处理的效果。
针对上述问题,本文提出一种基于加权形态非抽样小波分解(Weighted Morphological Un-decimated Wavelet Decomposition,WMUWD)的液压泵振动信号预处理方法。首先,在MUWD的一般框架下,提出WMUWD方法,利用特征能量因子对各分解层近似信号进行加权融合,以解决传统MUWD方法存在的信息遗漏问题,更好地提高特征信息比重;在此基础上,对WMUWD初始参数的选择进行分析,利用所定义的特征能量熵对参数组合进行优选,以避免主观经验对信号预处理效果的影响;最后,利用仿真信号和液压泵松靴故障的实测振动信号对本文所提出的WMUWD方法的有效性进行验证。
1 基于WMUWD的振动信号预处理
1.1 WMUWD基础运算
设集合Vi和Wi分别为第i层信号空间和第i层细节空间,T()为形态算子,文献[9]给出了传统MUWD方法的基础运算框架:

通过分析MWUD的基础框架可知,其关键运算点在于形态算子T( )的选择[12]。常用的有平均组合算子、形态差值算子、形态梯度算子以及混合算子[13-14]。考虑到液压泵自身结构特点以及信号预处理需求,本文选择形态差值算子。形态差值算子同时包含黑Top-Hat和白Top-Hat变换,可以同时提取信号中的正负脉冲[15]。因此,WMUWD的基础运算可描述为:
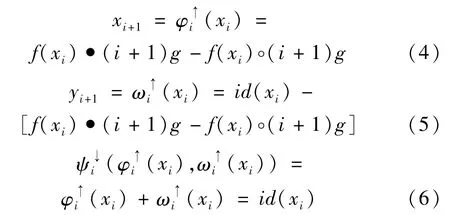
式中,f(x)为原始信号,“°”和“·”分别表示形态开和形态闭运算,g为结构元素,常用的有三角元素、扁平元素、半圆元素等,在无法或难以获得信号明显形态特征的情况下,常常选用形状最简单、运算速度最快的扁平元素用于提取冲击特征,因此,本文选用扁平元素进行研究。(i+1)g表示对结构元素进行i次膨胀操作。通过分析可知:在每一层的分解运算中,WMUWD通过式(4)中信号分析算子的形态差值运算,从前一层的近似信号中提取故障信息成分,保留在本层分解所得的近似信号中,作为下一层分解的原始信号。
1.2 WMUWD加权融合指标的构建
通过对WMUWD基础算法的分析,可以很清楚地看到,在每一层分解所得的近似信号中都不同程度地包含着特征信息,为了能够有效利用这些信息,首先需要确立相应的融合指标以衡量不同近似信号对特征的贡献程度,以计算WMUWD的融合权值。通过分析可知,每一层近似信号虽然包含了不同量的特征信息,但也或多或少的存在噪声干扰信息,因此需要选择对特征信息敏感度高的融合指标,以保证融合过程中提高故障信息含量的同时尽可能地减少噪声干扰。
通过查阅相关文献,常用的权重指标有均方根值、脉冲指标、峭度指标以及特征频率幅值。但是,均方根值对早期故障不敏感,脉冲指标和峭度指标的稳定性较差,特征频率幅值对故障后期敏感性不高。因此,从特征的敏感性与动态稳定性综合考虑,本文定义特征能量因子(FEF)为WMUWD的融合指标,它表示在频域内,特征频率前n倍频的局部能量占总能量的百分比值。其表达式为:
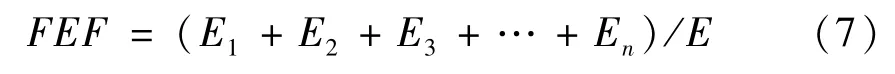
式中,En表示n倍特征频率处的能量值,本文取n=3(特征频率及其二、三倍频的能量在所有倍频中占有绝对的优势,因此具有代表性)。很显然,FEF对特征信息具有较高敏感性,能够较好地描述信号冲击脉冲的提取效果,其值越大,冲击成分的提取效果越好。
为了进一步分析FEF在特征敏感性和动态稳定性方面的优势,采用文献[16]的仿真信号对FEF与传统指标(均方根值z1、脉冲指标z2、峭度指标z3、特征频率幅值z4)的效果进行对比分析。WMUWD算法参数设置相同,随机选取某一层近似信号作为参考信号(以第三层为例),分别计算其不同退化阶段的FEF和z1-z4值,经标准化处理后,结果如图1所示。仍采用文献[16]的仿真信号,将噪声强度分别设置为1-10,随机选取其某个时间段数据(以第5s为例),计算FEF和z1 -z4值,结果如图2所示。

图1 加权指标随性能退化程度的变化Fig.1 Changes of weighting indexes along with aggravation
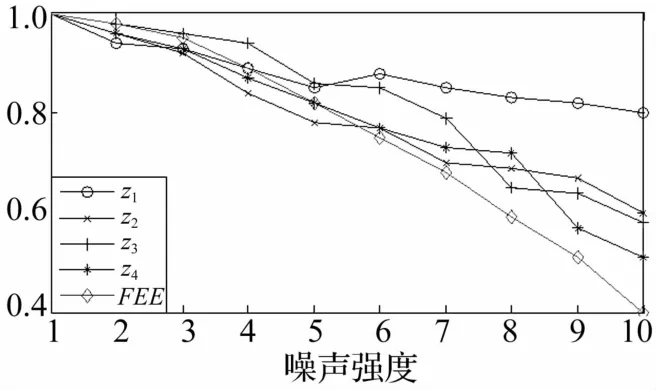
图2 加权指标随噪声强度的变化Fig.2 Changes ofweighting indexes along with noises
由图1可以看出,z1具有较好的稳定性,但对早期故障敏感性差;z2、z3对早期故障敏感性高,但随故障程度变化波动性大,整体稳定性不好;z4对故障后期敏感性不够高;与上述传统指标相比,FEF无论在对故障敏感性方面,还是在稳定性方面,都具有较明显的优势,这与前面分析所得到的结论是一致的。图2从噪声的角度描述了指标的动态特性,很明显,随噪声强度地提升,FEF呈现很平稳下降趋势,具有相对良好的动态变化特性。因此,以FEF作为加权融合指标,表征近似信号对特征贡献度,能够较好地保证对特征信息的充分利用。
1.3 基于WMUWD的振动信号加权重构
设形态非抽样小波的分解层数为N,振动信号各分解层近似信号为xi,i=1,2,…,N,对应的特征能量因子为FEFi,i=1,…,N,则可以得到其融合权值ki:

根据上一节对FEF特性的分析可知,对特征贡献大的近似信号其FEF也相对大,对应的其加权系数ki也大。加权融合重构的信号xFinal可描述为:
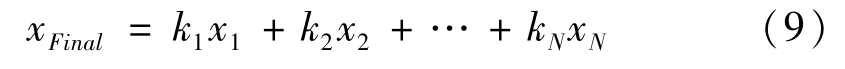
由于包含了对各分解层特征信息的综合利用,因此理论上讲,重构信号较融合前特征信息量得到了改善,信噪比得到了有效提高。基于WMUWD的液压泵振动信号预处理方法流程图如图3所示。
2 WMUWD参数优选
通过分析可知,WMUWD主要涉及两个参数:分解层数N和扁平结构元素初始长度L。对于参数N:①如果取值过大,则分解后的细节信号所含信息成分极少,近似信号的信息成分将不会随着N值继续增大而改变,导致运算复杂性增加;②若取值过小,则细节信号所包含的信息成分过于丰富,导致近似信号中的信息利用率不高,融合后的特征信息不明显。

图3 基于WMUWD的振动信号预处理流程图Fig.3 Flow chart for preprocessing of vibration signal based on WMUWD
对于参数L:①若取值过大,则能够提取的信号脉冲信息将会减少,导致部分特征信息的遗漏;②若取值过小,则在信号融合重构过程中很容易掺入噪声成分。
因此,不同组合会产生不同的预处理效果。针对此问题,本文提出融合能量熵(Fusion Energy Entropy,FEE)作为衡量不同参数组合下WMUWD预处理效果的指标。对于每一个参数组合(假设N=n,L=l),令Ei表示各层近似信号的能量值。则FEE可描述为:

由式(10)可知,FEE能够表征信号的复杂性,衡量对特征信息的利用程度。FEE越小,信息利用越充分,信号成分越单纯,特征信息越明显,预处理效果越好。
在此基础上,本文将给出一套完整的N与L优选方法,以避免基于主观经验选择对预处理效果的影响。具体步骤可描述为:
(1)利用局部极值间隔法确定参数N的范围:
①对信号序列进行搜索,得到局部极大值和极小值集合:
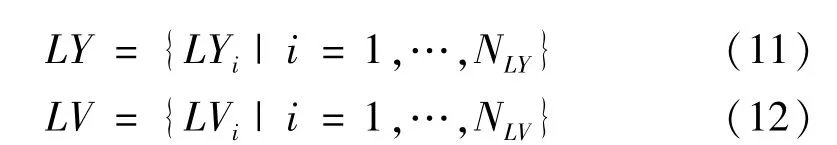
式中,NLY和NLV分别表示局部极大值点数和局部极小值点数。
②经过计算,得到局部极大值和极小值间距分别为:

式中,‘「·⌉'和‘⌊·⌉'分别表示向上取整运算和向下取整运算。
(2)由于经过多尺度变化后,L的最大值应不超过信号的脉冲周期[17]。结合参数N,可以确定L的取值:
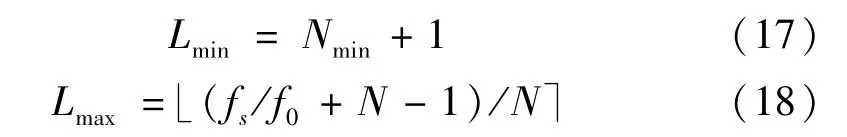
式中,fs表示采样频率,f0表示特征频率。
(3)根据所得取值范围,计算出N与L的组合数:

(4)根据公式(10)计算每个参数组合下的FEE值,选择最小FEE所对应的值,即为最优N和L组合。
3 仿真信号分析
为了验证所提出的WMUWD方法的有效性,本节将采用仿真信号[16]进行研究。设置采样频率fs=1 024 Hz,采样时间t=1 s,采集仿真信号x(t):
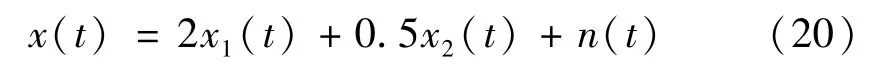
可以看出,x(t)主要由三部分组成:故障信号x1(t)、谐波信号x2(t)以及白噪声n(t)。x1(t)为模拟滚动轴承故障产生的周期性指数衰减冲击信号,冲击频率为f0=16 Hz,每周期内冲击函数为e-200tsin(2π× 256t),共振频率为256 Hz;x2(t)模拟谐波信号cos(2π×40t)+cos(2π×50t),包含40 Hz和50 Hz两个频率成分,差频为10 Hz。x(t)的时域和频域图(功率谱)分别如图4、图5所示。
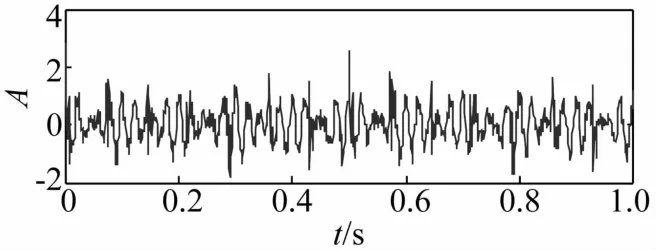
图4 仿真信号时域图Fig.4 Time domain of simulation signal
由图5可以看出,信号在共振频域256 Hz处有明显的调制现象,且故障特征频率16 Hz完全湮灭在噪声中。接下来,将利用本文所提出的WMUWD方法对信号进行预处理。
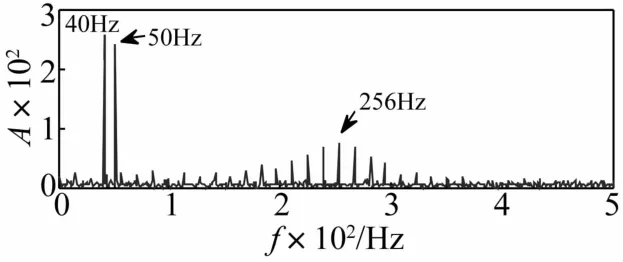
图5 仿真信号频域图Fig.5 Frequency domain of simulation signal
①分解层数N与结构元素L的优选
首先,确定N的范围:通过对信号序列局部间隔的分析,由式(11)~(16)可得:
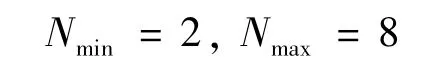
由前面分析可知,N的每一个值均对应L的一个取值范围,而fs=1 024 Hz,f0=16 Hz,根据式(17)~(18)计算得到的L取值见表1。

表1 分解层数与结构元素初始长度值Tab.1 The values of decomposition layers and initial length of structure element
由式(19)可得N与L共有97种组合。利用式(10)计算每种组合下WMUWD重构信号的FEE,结果如图6所示,图7为FEE在(0,0.05)取值区间的放大图。
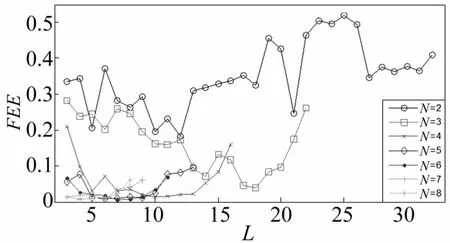
图6 FEE随参数N与L的变化曲线Fig.6 The curve of FEE with the changes of parameters of N and L
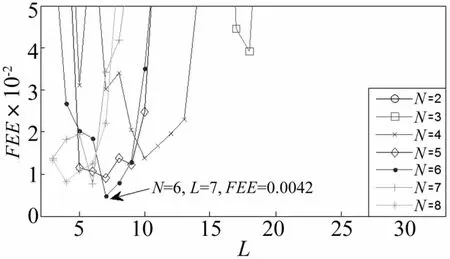
图7 FEE在0-0.05区间的变化情况Fig.7 Changes of FEE ranges from 0 to 0.05
图6给出了不同参数值组合下共97组FEE数值。每条曲线分别代表N取2-8时,FEE值随L取值的变化情况。每个N值所对应的FEE最小值分别为{0.184 0,0.038 9,0.013 5,0.009 1,0.004 2,0.007 9,0.008 4}。图7清楚地显示了(0,0.05)区间内FEE的取值情况,很明显,当N=6,L=7时,能够得到FEE的最小值0.004 2,表明此时的WMUWD预处理效果最佳,信号成分简单,特征信息成分突出。
②基于WMUWD的信号预处理效果分析
利用参数N=6,L=7的WMUWD方法对仿真信号进行预处理。设置结构元素g0=[0 0 0 0 0 0 0],分解层数N=6,由式(4)~(6)对信号进行分解。由式(7)对计算各层近似信号的FEF,结果为:{0.302 8 0.041 1 0.235 7 0.074 1 0.008 2 0.006 9}。因此加权融合权值为:k1=0.453,k2=0.061,k3=0.352,k4=0.111,k5=0.013,k6=0.010,根据式(9)对近似信号进行加权融合,重构信号为:
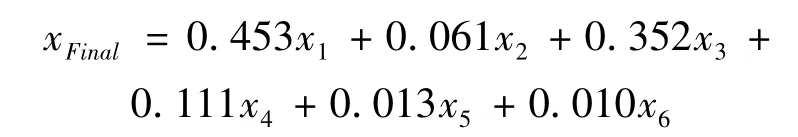
其频域效果如图8所示。
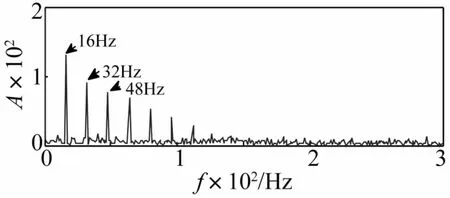
图8 WMUWD对信号的预处理效果Fig.8 Effect of preprocessing of the signal based on WMUWD
图8为WMUWD对信号预处理后的功率谱图,与原始信号相比,能够很清晰地看到特征频率16 Hz及其2、3倍频,而谐波干扰40 Hz、50 Hz得到了有效的抑制,且256 Hz处的调制现象也得到了改善。为了更好地说明该方法的优越性,对比加权融合前后的效果,分别计算第1~6层近似信号以及文献[9]所提出的传统MUWD方法预处理结果的信噪比参数SNR以及FEF结果见表2。
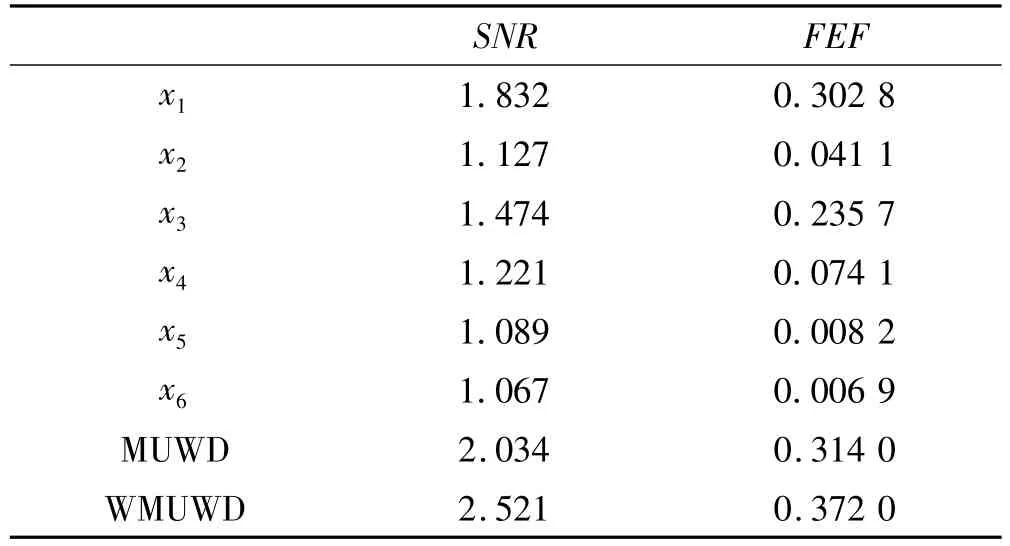
表2 预处理效果对比Tab.2 The comparison ofpreprocessing effects
通过对比表2的结果,可以看出,WMUWD预处理的信号效果优于任意分解层近似信号,与文献[9]的MUWD相比,无论是FEF还是SNR都有不同程度的提高,具有一定的优越性。
4 实验分析验证
为验证本文所提出方法的有效性与实用性,将该方法应用于液压泵松靴故障(如图9所示)振动信号预处理中。液压泵型号为力源L10V28,共有9个柱塞,驱动电机型号为YE2-225M-4,额定转速为1 480 r/min,周期为0.041 s。将振动加速度传感器安装在泵端盖处(如图10所示)。采集振动信号,采样频率为12 kHz,利用DH-5920动态信号测试分析系统将采集到的振动信号存入电脑。

图9 松靴故障Fig.9 The fault of loose slipper

图10 振动传感器的安装Fig.10 Installation of vibration sensor
所采集的松靴故障振动信号的时域和频域图(功率谱)分别如图11、图12所示。

图11 松靴故障信号时域图Fig.11 Time domain of loose slipper signal

图12 松靴故障信号频域图Fig.12 Frequency domain of loose slipper signal
通过分析可知:在时域上,每个周期内有9个冲击,这主要是由液压泵的结构决定的,与液压泵每旋转一周9个柱塞都冲击斜盘的情况相符;在频域上,故障信号存在明显的调制现象。由于液压泵轴的实际转速为1 480 r/min,转轴频率为1480/60=24.67 Hz,而柱塞泵有9个柱塞,因此,液压泵振动信号固有冲击频率为24.67×9=222 Hz;而对于单松靴故障,其特征频率理论上应该等于或接近转轴频率24.67 Hz。但是,从图可以看出,无论是固有频率还是故障特征频率均湮灭在噪声干扰中。因此,采用本文所提出的WMUWD方法对液压泵信号进行预处理。
首先,通过对信号序列局部间隔的分析,由公式(11)~(16)可得:Nmin=2,Nmax=10。因为fs=12 000 Hz,f0=24.6 Hz,根据公式(17)~(18)计算得到的L取值见表3。

表3 分解层数与结构元素初始长度值Tab.3 Values of decomposition layers and initial length of structure element
由公式(19)可得不同的N与L共有949种组合。利用公式(10)计算每种组合下的FEE,能够得到9条曲线及949组数值。N=2~10所对应的最小FEE值为{0.053 7,0.040 8,0.043 1,0.035 8,0.037 1,0.041 3,0.040 9,0.043 1,0.042 8}。图13为FEE在(0.03,0.05)取值区间的放大图。
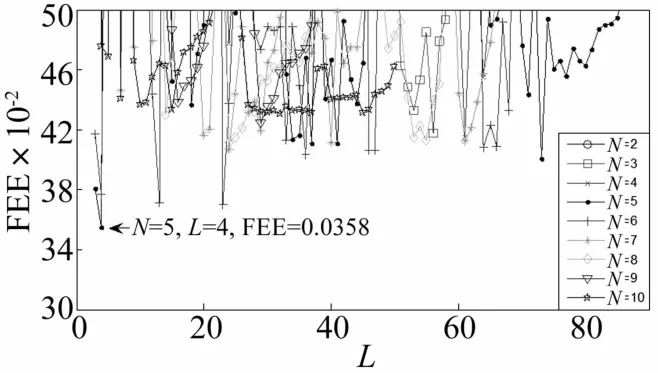
图13 FEE随N与L变化的曲线图Fig.13 The curve of FEE with the change of parameters of N and L
图13清楚地显示了当N=5,L=4时,FEE达到最小值0.035 8,表明此时的WMUWD预处理最佳,信号成分简单,特征信息成分突出。
因此,设置结构元素g0=[0 0 0 0],分解层数N=5,由公式(4)~(6)对信号进行分解。由式(7)对计算各层近似信号的FEF,结果为{0.028 7,0.022 6,0.030 9,0.035 6,0.026 8}。因此加权融合权值为:k1=0.198,k2=0.156,k3=0.214,k4=0.246,k5=0.186,根据公式(9)对近似信号进行加权融合,重构信号为:其频域效果如图14所示。
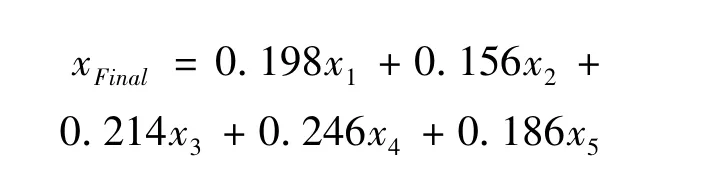
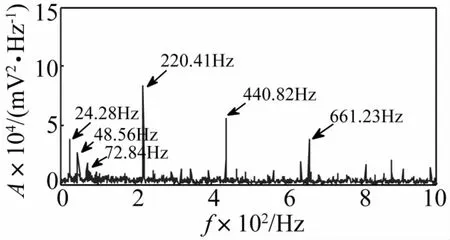
图14 WMUWD对液压泵故障信号的预处理效果Fig.14 The effect of preprocessing for fault signal of hydraulic pump based upon WMUWD
从图14可知,通过WMUWD对故障信号的预处理,可以很清晰地看到液压泵松靴故障特征频率24.28 Hz(24.28 Hz≈24.67 Hz)和其倍频以及液压泵的固有振动频率220.41 Hz(220.41 Hz≈222 Hz)和其倍频,原信号存在的噪声干扰以及调制现象得到有效解决。为了进一步验证算法的有效性,采用文献[9]中的传统MUWD方法对信号进行预处理,结果如图15所示。
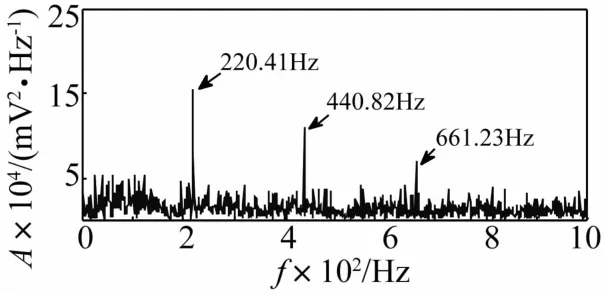
图15 MUWD对液压泵故障信号的预处理效果Fig.15 The effect of preprocessing for fault signal of hydraulic pump based upon MUWD
从图15可以看出,传统MUWD方法由于仅以最高分解层近似信号作为预处理结果,遗漏了部分特征信息,导致预处理后仅仅能得到固有频率220.41 Hz及其倍频,而松靴故障频率仍湮灭在噪声干扰中。分别计算图16MUWD方法预处理结果和图15WMUWD方法预处理结果的FEF值,与1-5近似信号FEF值汇总至表4。
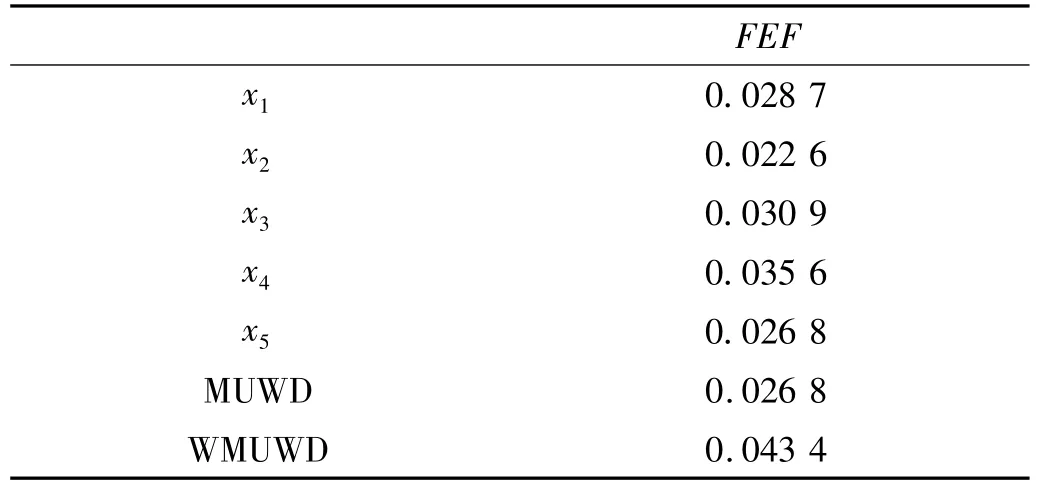
表4 预处理效果对比Tab.4 The comparison of preprocessing effects
通过分析表4可知,图16所应用的传统MUWD方法的预处理结果正好是本文WMWUD方法的第5分解层近似信号,特征信息比重相对较低,这主要是由于对其它分解层信息遗漏所致;而WMUWD方法由于采用了融合处理以及参数优选,能够有效地利用包含在各分解层近似信号的特征信息,因此,特征信息比重较传统MWUD方法以及各层近似信号都有了显著提高,取得了较好的预处理效果。
5 结 论
针对轴向柱塞液压泵振动信号非线性强、预处理效果不理想的问题,本文以MUWD框架为基础,提出了一种基于WMUWD的特征提取方法,通过对各分解层近似信号的融合,有效地提高了特征信息比重;在此基础上,给出了一套较系统的参数优选方法,避免了主观经验对预处理结果的影响。仿真信号以及液压泵实测信号的验证表明,该方法能够有效地利用特征信息,达到较理想的预处理效果,对实现基于状态的维修具有一定的促进意义。
[1]唐宏宾,吴运新,滑广军,等.基于EMD包络谱分析的液压泵故障诊断方法[J].振动与冲击,2012,31(9):44-48.
TANG Hong-bin,WU Yun-xin,HUA Guang-jun,et al.Fault diagnosis of pump using EMD and envelope spectrum analysis[J].Journal of Vibration and Shock,2012,31(9):44-48.
[2]Gan Yu,Sui Li-fei,Wu Jiangfei,et al.An EMD threshold de-noising method for inertial sensors[J].Measurement,2014,49:34-41.
[3]Yan Ru-qiang,Robert X.Gao.Wavelets for fault diagnosis of rotary machines:A review with applications[J].Signal Processing,2014,96:1-15.
[4]Goutsias J,Heijmans H J A M.Nonlinear multi resolution signal decomposition schemes,part 1:morphological pyramids[J].IEEE Transaction on Image Processing,2000,9(11):1862-1876.
[5]Heijmans H J A M,Goutsias J.Nonlinear multi resolution signal decomposition schemes,part1:morphologicalwavelets [J].IEEE Transaction on Image Processing,2000,9(11):1897-1913.
[6]Zhang JF,Smith JS,Wu Q H.Morphological un-decimated wavelet decomposition for fault location on power transmission lines[J].IEEE Transactions on Circuits and Systems,2006,53(6):1395-1402.
[7]黄兵峰,沈路,周晓军,等.基于形态非抽样小波分解的滚动轴承故障特征提取[J].农业机械学报,2010,41(2):204-207.
HUANG Bing-feng,SHEN Lu,ZHOU Xiao-jun,et al.Fault feature extraction of rolling element bearing based on morphological undecimated wavelet decompostion[J].Journal of Agricultural Engineering,2010,41(2):204-207.
[8]孙志辉,吕文泉.基于形态非抽样小波和S变换的轧机振动信号分析[J].北京科技大学学报,2013,35(3):366-370.
SUN Zhi-hui,LÜWen-quan.Signal analysis of rolling mill vibration based on morphological un-decimated wavelets and S-transform[J].Journal of University of Sceince and Technology Beijing,2013,35(3):366-370.
[9]章立军,阳建宏,徐金梧,等.形态非抽样小波及其在冲击信号特征提取中的应用[J].振动与冲击,2007,26 (10):56-59.
ZHANG Li-jun,YANG Jian-hong,XU Jin-wu,et al.Morphological undecimated wavelet and its application to feature extraction of impulsive signal[J].Journal of Vibration and Shock,2007,26(10):56-59.
[10]Morenilla A J,Carmona R M,Romero J L S.Mathematical morphology for design and manufacturing[J].Mathematical and Computer Modeling,2011,54(7):1753-1759.
[11]Cousty J,Najman L,Dias F,etal.Morphological filtering on graphs[J].Computer Vision and Image Understanding,2013,117(4):370-385.
[12]Li Bing,Zhang Pei-lin,Wang Zheng-jun.Gear fault detection using multi-scale morphological filters[J].Measurement,2011,44(10):2078-2089.
[13]HeWei,Jiang Zhi-nong,Qin Qiang.A jointadaptivewavelet filter and morphological signal processing method for weak mechanical impulse extraction[J].Journal of Mechanical Science and Technology,2011,24(8):1709-1716.
[14]Hao R J,Chu F L.Morphological un-decimated wavelet decomposition for fault diagnostics of rolling element bearings [J].Journal of Sound and Vibration,2009,4(1):1164 -1177.
[15]王冰,李洪儒,许葆华.一种多元素多尺度形态非抽样小波分解方法[J].轴承,2013(5):43-48.
WANG Bing,LI Hong-ru,XU Bao-hua.A kind of multelement and multi-scale morphological undecimated wavelet decomposition method[J].Bearing,2013(5):43-48.
[16]徐东,徐永成,陈循,等.基于EMD的灰色模型的疲劳寿命预测方法研究[J].振动工程学报,2011,24(1):104-110.
XU Dong,XU Yong-cheng,CHEN Xun,et al.Residual fatigue life prediciton based on grey model and EMD[J].Journal of Vibration Engineering,2011,24(1):104-110.
[17]Li Bing,Zhang Peilin,Wang Zheng-jun.Gear fault detection using multi-scale morphological filters[J].Measurement,2011,44(10):2078-2089.
Preprocessing algorithm for vibration signals of a hydraulic pum p based upon WMUWD
SUN Jian,LIHong-ru,WANGWei-guo,XU Bao-hua
(Ordnance Engineering College,Shijiazhuang 050003,China)
In allusion to the problem that the vibration of an axial piston pump is of strong nonlinearity,and the fault feature information is affected seriously by noises,a novelmethod for vibration signal preprocessing based on the weighted morphological un-decimated wavelet decomposition(WMUWD)was proposed.The WMUWD method was presented under the general frame of the morphological un-decimated wavelet decomposition.In order to increase the useful feature information content,approximate signals of various decomposition layerswere weightedly fused according to their contributions to fault features,they weremeasured with the feature energy factors.On this basis,the initial indexes ofWMUWD were analyzed and a systematic method for optimal selection was provided.The validity of the method was testified by using the data of simulated signals and real vibration signals.
signal preprocessing;morphological un-decimated wavelet decomposition;weighted fusion;hydraulic pump
TH212;TH213.3
A
10.13465/j.cnki.jvs.2015.21.017
国家自然科学基金资助项目(51275524)
2015-04-02 修改稿收到日期:2015-05-27
孙健男,博士生,1987年生
李洪儒男,教授,博士生导师,1963年生

