基于随机减量法的非平稳激励下模态参数识别

罗 钧，刘 纲，2，黄宗明，2

（1.重庆大学土木工程学院，重庆 400045；2.山地城镇建设与新技术教育部重点实验室，重庆 400045）

基于随机减量法的非平稳激励下模态参数识别

罗 钧1，刘 纲1，2，黄宗明1，2

（1.重庆大学土木工程学院，重庆 400045；2.山地城镇建设与新技术教育部重点实验室，重庆 400045）

针对现有结构模态参数识别方法平稳激励假定的不足，提出了一种非平稳激励下的结构模态参数识别方法。以白噪声调幅激励、调幅相关激励和频率幅值调制共三类非平稳随机激励为对象，采用演化谱理论推导了随机激励分段叠加后的均值和方差表达式，然后在此基础上对传统的随机减量法进行拓展，将非平稳激励下模态参数识别问题转化为结构自由振动曲线的模态参数识别，最后利用特征实现算法识别结构的模态参数。通过一个悬臂梁数值模型和两层实验室钢框架进行验证，识别结果表明运用该算法可以准确识别出非平稳激励下系统的固有频率和振型，且固有频率的识别误差在2%以内，具有较高的识别精度。

随机减量法，非平稳环境激励，模态参数识别，自由振动

桥梁、输电塔和高层建筑等大型实际结构模态参数的识别，是进行有限元模型修正、损伤识别和优化设计等工作的基础。传统的模态参数识别方法多采用人工在结构上施加激励，是在结构输入、输出均已知的情况下进行结构模态参数的识别。但对于大型土木结构而言，结构构件多、几何尺寸大，很难甚至无法采用人工激励的方式进行激振，因此，依靠车辆、脉动风、地脉动和地震动等随机激励方式（通常无法量测）识别出结构模态参数具有重要的理论意义和现实工程价值，现已发展为土木工程领域内一个重要的研究方向——工作模态分析。

经过30多年的研究，业界已提出了很多的工作模态分析方法，大致可分为基于频域、时域和时频域共三类方法。在频域内，基于白噪声激励下结构体系响应的互功率谱估计和奇异值分解，Brincker等［1］提出了频率域分解法；Guillaume等［2］在激励和响应均可测量的前提下，基于权矩阵分数模型提出了PolyMax方法；Peeters［3］将PolyMax的应用范围扩展到白噪声激励的情况下，推导了利用输出功率谱进行模态参数识别的PolyMax方法。在时域内，Van Overschee等［4］将LQ分解和SVD分解引入子空间识别，提出了适用于白噪声激励的随机子空间识别法。在时频域内，Sun等［5］提出了基于协方差驱动的小波识别方法，由于涉及协方差计算，该方法并不适用于非平稳激励情况。

为便于理论推导，以上方法均假设随机激励是具有时间不相关性的高斯白噪声，即空间上各点激励为互不相关的平稳随机过程。但这一假设与真实激励并不相符，例如胡强等［6］通过对大地脉动实测数据的分析，表明大地脉动含有丰富的低频周期分量，具有随机性和非平稳性。实测脉动风也有一定的主要频率和方向，且在时域具有明显的间歇性和非高斯性［7］。现有工作模态分析方法理论假设的不足，导致识别精度远小于已知激励的模态参数识别方法，限制了其在大型土木结构中的应用。

大量研究表明，地脉动、脉动风荷载和地震动等环境激励都可认为是均值为0，方差随时间改变的非平稳随机信号［7－8］。本文以土木结构中以上常用的非平稳随机激励为主要研究对象，从演化谱的角度，通过理论推导得出其统计特性，然后对传统的随机减量法进行扩展，并利用扩展后的随机减量法将结构非平稳响应转化为结构的自由衰减信号，再利用特征系统实现算法（ERA）识别结构的模态参数。通过对白噪声调幅、相关调幅和频率幅值调制这三类非平稳激励下结构模态识别算例表明，所提方法能成功实现非平稳随机激励下结构模态参数的识别，从而为大型土木结构模态参数的获取提供了一种有效的新方法。

1 非平稳随机荷载的统计特性

地脉动等随机荷载往往无法准确测量。但在理论分析上，演化谱作为平稳随机信号谱分解的推广，广泛应用于地震动、风荷载等非平稳信号的时频特性分析和数值模拟［9－10］，故以演化谱为工具，研究非平稳随机荷载的统计特性。

1.1 非平稳随机荷载的均值和方差

从信号的角度，非平稳随机荷载可视为非平稳随机信号。对演化谱而言，该非平稳随机信号可认为是白噪声信号通过某线性时变滤波系统所得的输出［11］，例如地脉动可理解为在场地土底部输入的白噪声通过场地土后的输出。当均值为0、方差为的白噪声e（t）通过一个线性时变滤波系统的输出为：

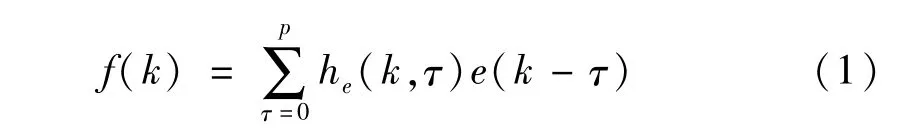
式中：f（k）表示k×dt时刻的非平稳随机荷载；he（k，τ）表示k×dt时刻线性滤波系统脉冲响应函数的第τ个时延值，e（k－τ）表示第（k－τ）×dt时刻的白噪音信号；p为整数，是时延的最大长度值；dt为离散采样的时间间隔。

如假定线性时变滤波系统为确定性系统，则根据白噪声信号在时间上具有相互独立的特性，可得非平稳随机荷载f（k）的均值和方差为：

1.2 非平稳随机荷载分段叠加的统计特性

将非平稳随机荷载f（k）分段叠加后求平均，即将f（k）分为长度为P的n段，然后将各段信号进行平均，即：

式中，kl为第l段数据的起始时间。考察平均后所得信号F的均值和方差：

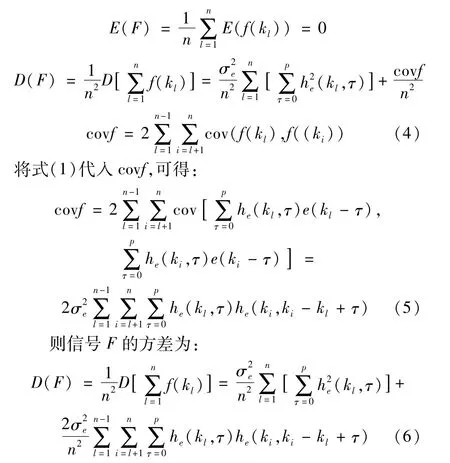
1.3 信号F在不同荷载形式下的方差特性

从式（4）、（5）可知，将非平稳随机荷载f（k）分段平均所形成信号F的方差是时间的变量，下面就线性滤波系统的脉冲响应函数he（k，τ）是否与时间相关来分析该方差的特性。

当脉冲响应函数he（k，τ）为时间的独立函数时，即脉冲响应函数满足：

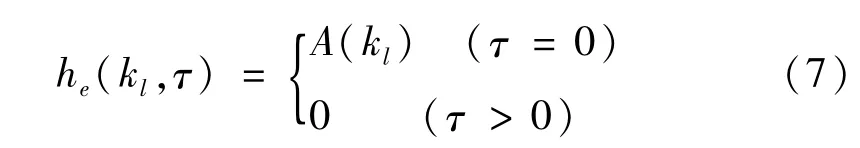
式中，A（kl）为调幅函数。此时，非平稳随机荷载f（k）为白噪声调幅信号。将式（7）代入式（4）、（5），可得叠加信号F的方差为：

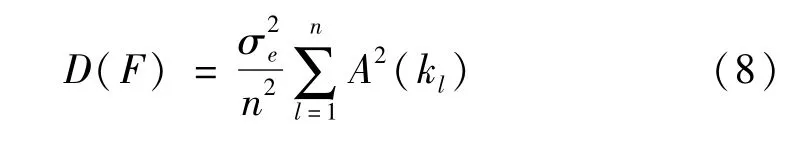
当脉冲响应函数he（k，τ）为时间相关函数时，则所得的非平稳随机荷载f（k）在各瞬时也是相关的，例如地脉动、脉动风荷载和地震动等激励均符合这一特性。此时若假设非平稳随机荷载f（k）分段时，各段信号之间的间隔大于线性滤波系统自由衰减振动的时间常数，则可得：

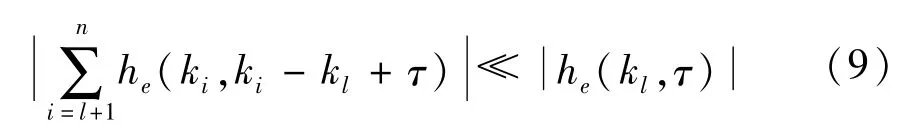
此时，公式（6）中的第2项将比第1项小得多，可以忽略，则叠加信号F的方差可简化为：

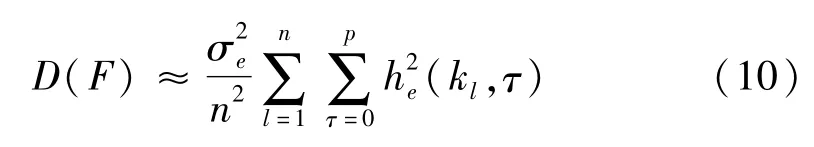
从式（4）、（9）和（10）可知，无论零均值非平稳随机荷载为白噪声调幅信号，还是时间相关信号，经过分段叠加后的信号F的均值为0，方差随着叠加次数n的增加将逐步减小。

2 基于扩展随机减量法的模态参数识别

2.1 随机减量法的扩展

对单自由度结构体系，随机减量法首先选取某一阈值A，去截取随机激励下体系的响应信号，得到起点时刻为tk（k＝1，2，…，n），长度为s的n段时间序列信号，如图1所示。然后再对这n段信号叠加后求平均，从而得出体系的自由振动信号，

当随机激励满足零均值的高斯分布时，理论推导表明该振动信号为结构系统在初始位移情况下的自由衰减振动信号［12］。

下面分析零均值非平稳随机荷载作用下，随机减量法所得多自由度体系的自由振动信号δ（s）。对多自由度线性土木结构体系，其运动微分方程可表述为：

式中：M，C和K分别为体系的质量矩阵、阻尼矩阵和刚度矩阵；x为位移向量；f（t）为零均值非平稳的外荷载向量。

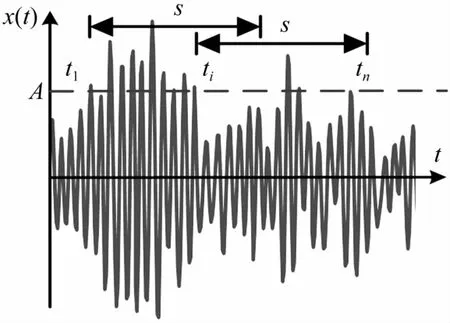
图1 随机减量法流程示意图Fig.1 Procedure of the Random decretion technique

由结构动力学基本原理，该线性结构体系第i自由度的位移响应可表示为多个模态位移响应的叠加，即：

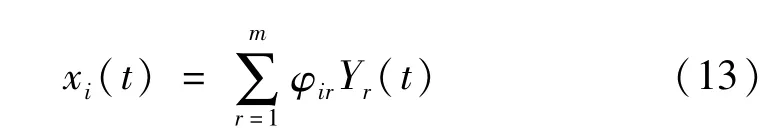
式中，φir为第r阶振型向量在第i个自由度上的数值；m为模态的阶数；Yr为第r阶模态位移响应。

按式（11）的方式截取信号进行平均，有：

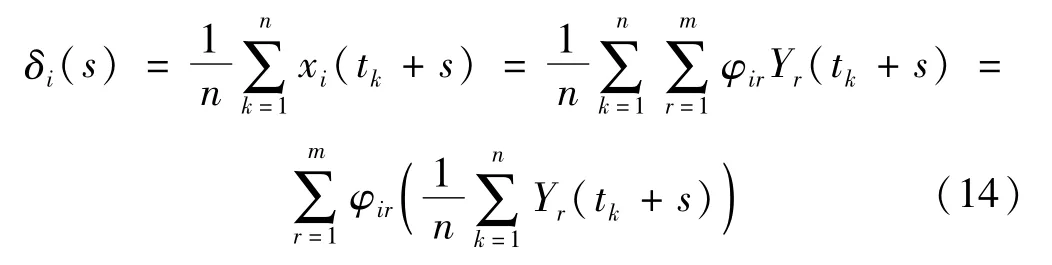
由式（14）可见，通过线性结构的模态分解，可将求第i自由度上的自由振动信号δi（s）转化为求各阶模态位移响应分段叠加再取平均。

因单位脉冲响应函数均具有衰减性，则可认为gr（t－τ）是有限长度的，同时考虑到模态荷载和模态脉冲响应函数具有单边性质，则有：

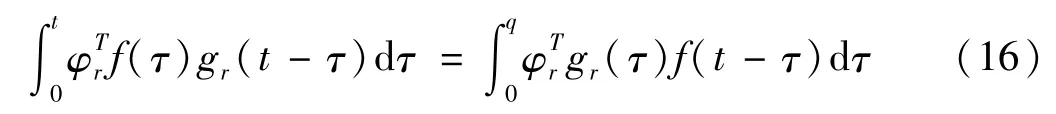
式中，q为模态脉冲响应函数的长度。

将式（15）和式（16）中的t换为tk+s，推导可得Yr（tk+s）的表达式：

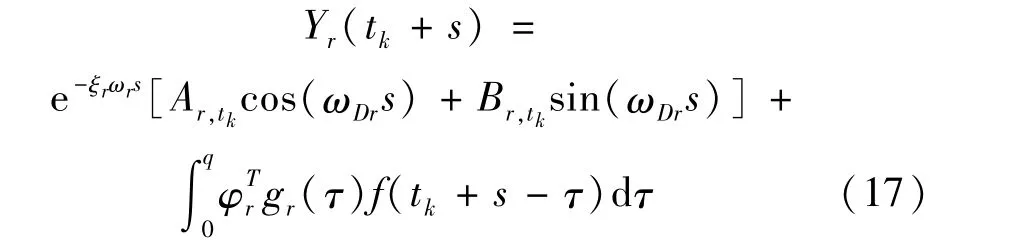
式中，Ar，tk，Br，tk分别为：

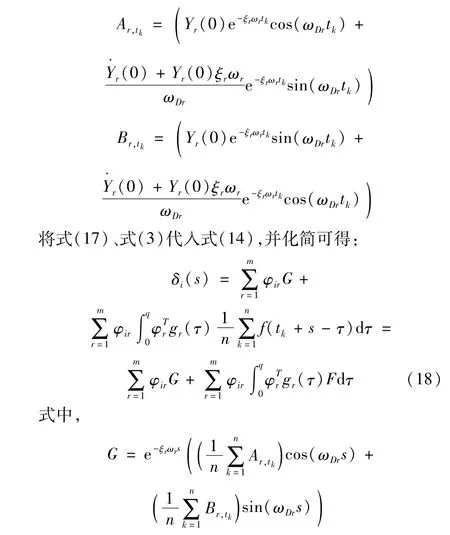
从式（18）可知，在零均值非平稳荷载作用下，随机减量法获得的信号可分为2项的叠加，第1项仅与结构自身及其初始模态位移和模态速度相关，第2项与非平稳外荷载相关。由第1节的推导，F的均值为0，方差随着随机减量法平均次数n的增加而趋近于0，故当n较大时，随机减量法信号δi（s）中第2项的值将趋近于0。

值得注意的是，当外荷载为平稳激励时，式（18）中的第2项中F的均值为0，方差随n增大趋近于0，故第2项的值在0附近极小范围波动；当外荷载为非平稳激励时，式（18）中的第2项中F均值为0，同时考虑到F的方差随n增大而逐渐减小，故可将第2项视为噪声项，则非平稳激励下采用随机减量法所得信号为包含噪声的自由振动衰减信号。本文将随机减量法从处理白噪音信号扩展到处理非平稳信号，称为扩展随机减量法。

2.2 模态参数的识别

为提高非平稳激励下扩展随机减量法所得信号的信噪比，本文首先采用奇异值消噪［14］对随机减量信号进行预处理，再利用文献［15］提出的改进特征系统实现算法进行土木结构体系模态参数的识别。进行非平稳激励下模态参数识别的流程如图2所示。

图2 非平稳激励下模态参数识别的流程图Fig.2 Procedure of themodal parameter identification under non-stationary excitation

3 算例及实验验证

3.1 数值算例

以一个悬臂梁模型说明扩展随机减量法在非平稳激励下的模态参数识别效果，如图3所示。梁总长为0.7 m，截面形状为矩形，宽取为30 mm，高取为3 mm。梁等间距划分为7段，模型采用模态阻尼假定，各阶阻尼比均为0.01。

在固定端分别施加白噪声平稳激励、白噪声调幅激励、相关调幅激励。白噪声调幅激励和相关调幅激励采用白噪声输入一个线性时变滤波系统的输出进行模拟。白噪声调幅激励模拟时采用的线性时变滤波系统脉冲响应函数为he1（t，τ），相关调幅激励模拟时采用的线性时变滤波系统脉冲响应函数为he2（t，τ），其表达式为：

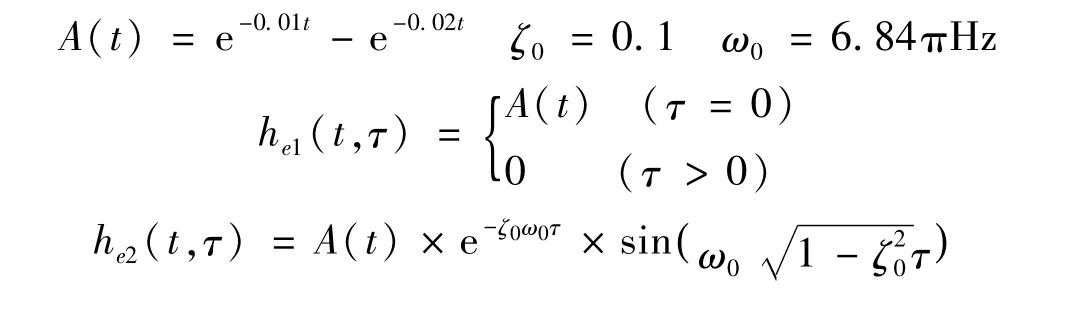
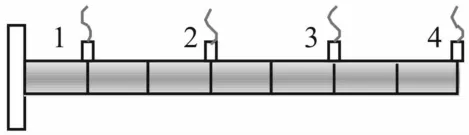
图3 悬臂梁计算模型Fig.3 The cantilever beam model

取图3中传感器位置处的加速度响应，采样频率为200 Hz，利用极值触发的随机减量法提取随机减量曲线。图4为参考测点为第2测点时，白噪声调幅激励和相关调幅激励下提取的第4测点随机减量曲线。图中右下角的小图为对应的激励曲线，横坐标为时间，单位为s，纵坐标为幅值，单位为m／s2。

值得注意的是，图4中图（a）和图（b）响应衰减规律有差别，这主要是由于自由衰减信号是多频率成分的组合信号，而在不同激励下将激起结构不同频率的信号，则自由振动的衰减信号主要表现为所激振频率的衰减规律。在相关调幅激励下，算例结构的自由振动响应以第一阶频率为主；而在白噪声调幅激励下，算例结构的响应在各阶模态处相差不大，加之一阶模态的衰减速率较其余模态阶次衰减速率明显偏小，因此频率成分较均衡的白噪声调幅激励下结构自由振动响应的衰减速率比以一阶频率为主的相关调幅激励下结构自由振动响应的衰减速率大，衰减快。

采用奇异值消噪技术处理后，截取前面信噪比较高的部分信号，利用特征系统实现算法识别悬臂梁的模态参数，频率、阻尼比、模态振型、模态能量容差分别取0.01、0.05、0.02、0.1。得到各激励形式下的识别结果如表1和图5所示。从识别结果可以看出，本文方法识别的频率和振型具有较高的精度，频率的最大相对误差仅为0.33%，振型的MAC值均为1。

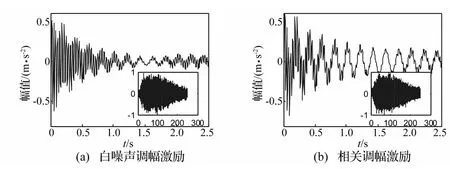
图4 不同激励形式下第4测点的随机减量曲线Fig.4 Random decrement curve of the fourth sensor under various loads

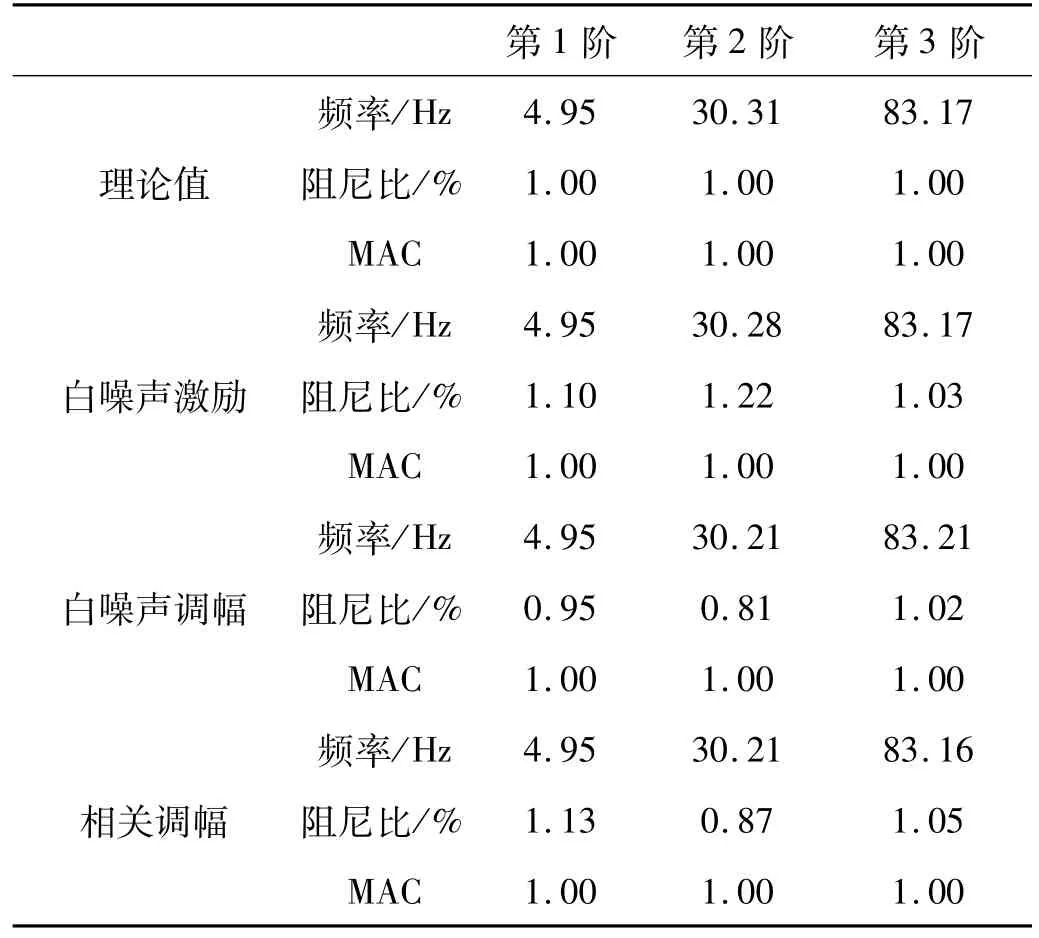
表1 各激励形式下悬臂梁的模态参数Tab.1 M odal parameters of cantilever beam under various loads

3.2 试验验证

采用宽65 mm，厚4 mm的钢板组成框架的梁和柱，并通过节点板和螺栓连接，每个节点板安装4颗螺栓，2颗与柱相连，2颗与梁或刚性基座相连，如图6所示。

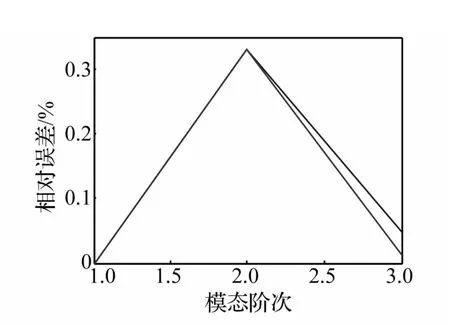
图5 各激励形式下识别的频率相对误差Fig.5 Relative error of frequency identified under various loads

图6 两层钢框架模型Fig.6 2－story steel frame

在梁柱节点处布置两个加速度传感器，下部的为测点1，上部的为测点2。为了采集较多的数据点，结构响应的采样频率为800 Hz。采用KDJ－50型电磁激振器在第一层右柱下侧输入激振信号。激励信号为白噪声调幅激励、相关信号调幅激励和地震动激励。白噪声调幅激励和相关信号调幅激励的构造方式与数值模拟相同，时间间隔取0.001 25 s。地震波选用1976 年7月27日我国唐山地震中密云水库台站地震记录，由于实际地震波的时间间隔为0.01 s，因此本文采用样条插值对地震波进行处理，使其时间间隔为0.001 25 s。

图7 不同激励形式下第2测点的随机减量曲线Fig.7 Random decrement curve of the 2th sensor under various loads

对采集的原始数据首先通过低通滤波，再利用极值触发的随机减量法提取随机减量曲线。图7为参考测点为第2测点时，白噪声调幅激励、相关调幅激励和地震激励下提取的第2测点随机减量曲线。由于试验中未测量激振力的大小，激励的大小由结构响应加以控制，故本图中右上角给出第2测点的响应信号，横坐标为时间，单位为s，纵坐标为幅值，单位为m／s2。

采用本文方法识别结构的模态参数，识别结果如表2所示。频率、阻尼比、模态振型、模态能量容差分别取0.01、0.2、0.02、0.1。由于模态参数的精确值未知，本文将脉冲激励下识别的模态参数作为精确值来衡量其余激励形式下的识别精度。从表2可以看出，本文方法可以较准确的识别出结构的频率和振型。然而阻尼比的识别误差较大，主要原因在于模态参数识别理论上的瑞雷阻尼假定、各阶模态成分的互相干扰、提取随机减量曲线的平均次数和噪声的影响。

表2 各激励形式下识别的模态参数Tab.2 M odal parameters of the steel frame under various loads

4 结 论

本文从演化谱的角度对随机非平稳激励荷载的非平稳特性进行分析，然后对传统的随机减量法进行扩展，将非平稳激励下模态参数识别问题转化为基于包含非平稳噪声自由振动曲线的模态参数识别，并利用特征系统实现算法（ERA）识别结构的模态参数。最后利用一个悬臂梁数值模型和两层钢框架实验讨论了激励为白噪声调幅、相关调幅和频率幅值调制下的模态识别精度，结果表明：

（1）作用于结构的随机激励可视为白噪声通过线性时不变系统的输出，通过假定线性时不变系统具有的不同特征，得到白噪声调幅、相关调幅和频率幅值调制三类具有零均值的非平稳激励（信号）。这三类信号分段叠加所得信号具有均值为0，方差随叠加次数增加而线性减小的特征。

（2）通过模态叠加法推导了非平稳激励下随机减量法的理论计算公式，结果表明在零均值非平稳随机激励下，随机减量所得结果为包含噪声的自由振动衰减信号。

（3）本文方法适用于零均值非平稳激励下工程结构的模态参数识别。数值算例和实验室模型的结构模态参数识别结果表明悬臂梁数值算例的固有频率的识别误差在1%以内，振型的MAC值为1.0；两层实验室钢框架结构的固有频率识别结果在2%以内，振型的MAC值为1.0。

（4）本文提出方法在实际高层建筑、大跨桥梁结构中的实际应用有待进一步研究。对高层建筑物和桥梁荷载输入及响应进行实测，研究输入、输出信号的特性并进行模态参数识别是本文后续研究的方向。

［1］Brincker R，Zhang L，Andersen P.Modal identification from ambient responses using frequency domain decomposition ［C］／／Proc.of，2000，18：625－630.

［2］Guillaume P，Verboven P，Vanlanduit S，et al.A polyreference implementation of the least-squares complex frequency-domain estimator［C］／／Proceedings of IMAC，2003，21：183－192.

［3］Peeters B，Vanhollebeke F，Van der Auweraer H.Operational PolyMAX for estimating the dynamic properties of a stadium structure during a football game［C］／／Proceedings of the IMAC，2005，23.

［4］Van Overschee P，De Moor B.Subspace identification for linear systems：theory，implementation，applications［C］／／status：published，1996.

［5］Sun Z，Chang C C.Covariance-driven wavelet technique for structural damage assessment［J］.Smart Structures and Systems，2006，2（2）：127－140.

［6］胡强，程耀东，齐津.大地脉动数据的分析及建模［J］.浙江大学学报，1997，31（6）：767－773.

HU Qiang，CHENG Yao-dong，QIJin.Analysis and modeling of earth pulsation data［J］.Journal of Zhejiang University，1997，31（6）：767－773.

［7］伊廷华，李宏男，王国新.基于小波变换的高层建筑脉动风速模拟与实测研究［J］.振动与冲击，2007，26（3）：13－18.

YI Ting-hua，LI Hong-nan，WANG Guo-xin.Expermental study and numerical simulation of fluctuating wind speed on top of a tall building based on wavelet transform［J］.Journal of Vibration and Shock，2007，26（3）：13－18.

［8］杜修力，陈厚群.地震动随机模拟及其参数确定方法［J］.地震工程与工程振动，1994，14（4）：1－5.

DU Xiu-li，CHEN Hou-qun.Random simulation and its parameter determination method of earthquake ground motion ［J］.Earthquake Engineering and Engineering Vibration，1994，14（4）：1－5.

［9］Failla G，Pappatico M，Cundari G A.A wavelet-based spectrum for non-stationary processes［J］.Mechanics Research Communications，2011，38（5）：361－367.

［10］丁幼亮，周广东，李万恒等.基于演化谱理论的桥梁风致响应非平稳性分析［J］.中国公路学报，2013，26（5）：54－61.

DING You-liang，ZHOU Guang-dong，LIWan-heng，et al.Nonstationary analysis of wind-induced responses of bridges based on evolutionary spectrum theory［J］.China Journal of Highway and Transport，2013，26（5）：54－61.

［11］王宏禹，邱天爽，陈喆.非平稳随机信号分析与处理［M］.北京：国防工业出版社，2008.

［12］李德葆，陆秋海.实验模态分析及其应用［M］.北京：科学出版社，2001.

［13］克拉夫RW，彭津J著.结构动力学［M］.2版.王光远等，译.北京：高等教育出版社，2006：177.

［14］孙鑫晖，张令弥，王彤.基于奇异值分解的频响函数降噪方法［J］.振动、测试与诊断，2009，29（3）：325－328.

SUN Xin-hui，ZHANG Ling-mi，WANG Tong.Noise reduction of frequency response function using singular value decomposition［J］.Journal of Vibration Measurement＆Diagnosis，2009，29（3）：325－328.

［15］章国稳.环境激励下结构模态参数自动识别与算法优化［D］.重庆：重庆大学，2012.

M odal parametric identification under non-stationary excitation based on random decrementmethod

LUO Jun1，LIU Gang1，2，HUANG Zong-ming1，2

（1.College of Civil Engineering，Chongqing University，Chongqing 400045，China；2.The Key Laboratory of New Technology for Construction of Cities in Mountain Area of the Ministry of Education，Chongqing University，Chongqing 400045，China）

Aiming at the shortcoming of the existingmodal parametric identification method with the assumption of stationary excitations，amodal parametric identification method under non-stationary excitation was presented here based on the radom decrementmethod.Firstly，the variance and the mean of the excitations were derived on the basis of the evolutionary spectral amplitude modulation theory for white noise amplitude modulation excitation，the related excitation with amplitude modulation and the non-stationary excitation with frequency and amplitude modulation.Then，the traditional random decrementmethod was expanded，and themodal parametric identification problem under non-stationary excitation was converted into a modal parametric identification problem based on free vibration response curves of structures.Finally，themodal parameters were identified using the eigen-system realization algorithms.The method was verified through a numerical model of a cantilevered beam and a two-story steel frame tests.The identification results showed that the proposed method can accurately identify natural frequencies and vibration modal shapes of the two structures under non-stationary excitation and the identification error for natural frequencies is less than 2%，it has a higher identification accuracy.

random decrementmethod；non-stationary environment excitation；modal parametric identification；free vibration response

TN911.7

A

10.13465／j.cnki.jvs.2015.21.004

中央高校基本科研业务费（CDJXS11200007）资助

2014－07－14 修改稿收到日期：2014－09－18

罗钧男，博士生，1986年5月生

黄宗明男，博士，教授，1957年5月生