基于层次分析法的青年人购房模型

张华

(山西建筑职业技术学院，太原 030006)

基于层次分析法的青年人购房模型

张华

(山西建筑职业技术学院，太原 030006)

为了解决青年人购房时难以决策的问题，根据所在城市情况，以首付款基本相同的楼盘为研究对象，应用层次分析法得到了购买商品住房的数学模型，从而用定量的方法解决了青年人购房决策问题.

层次分析法；数学模型；购房问题；决策

现在，青年人在购买商品住房时主要是通过定性分析的方法，凭借家人的意见以及楼盘在社会上的口碑主观判断做出决策方案.此处作者结合自身的购房考虑，利用层次分析法，对购房各考虑因素进行分析与讨论，依据建立的模型，用数学方法解决了青年人购房的决策问题.

1 购房影响因素的比较数据

通过对所在城市相关楼盘的了解以及购房知识的学习，结合自身，在首付款基本相同的情况下，对购房应考虑的因素做了以下几点归纳，主要有房屋地段、户型面积、质量与品牌、周边配套设施、物业管理情况、城市未来规划和生活设施配套情况等.将有购买意向的楼盘分为城市郊区楼盘、与工作单位同一城区楼盘、城市新建城区楼盘和与工作单位不同城区楼盘等类型，获得了以下调查分析数据(表格中分值为5分制，1表示一般，3表示满意，5表示非常满意，2，4表示界于以上相邻两者之间).

房屋所处地段比较(表1)，以相距工作单位的距离为重要依据；房屋户型面积比较(表2)，以付款基本相同的情况下面积越大越好；质量与品牌比较(表3)，以开发企业品牌与规模作为重要依据；周边配套设施比较(表4)，以周边有无学校、医院和大型超市等为重要依据；物业管理情况比较(表5)，以物业管理企业声誉与规模为重要依据；城市未来规划比较(表6)，以楼盘周边未来发展空间及出行交通环境变化趋势为重要依据；生活配套设施比较(表7)，以生活基础设施有无加入城市设施网络为重要依据.

表1 房屋地段比较

表2 户型面积比较

表3 质量与品牌比较

表4 周围配套设施比较

表5 物业管理情况比较

表6 城市未来规划比较

表7 生活配套设施比较

2 基于层次分析法的青年人购房模型

对购房决策问题应用AHP法，在以上调查分析分值数据的基础上，建立层次分析模型.

2.1 层次结构图(图1)

2.2 构造准则层对目标层成对比较矩阵对准则层中7个影响因素相对于目标层(选择的购房楼盘)做成对比较矩阵C，得到了比较结果.(表8).通过计算C的最大特征值［1，2］λmax＝7.1476，由文献［1－5］知RI＝1.32，所以

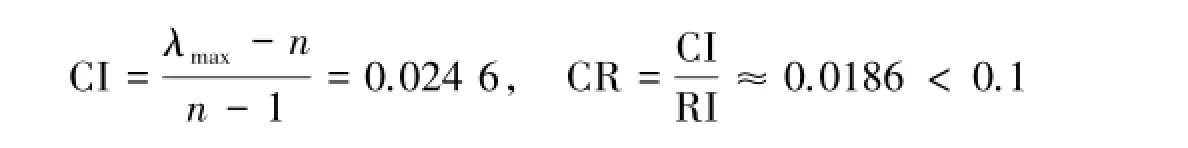
这说明准则层C相对于目标层的成对比较矩阵符合一致性检验要求，是可以接受的.利用和法［4］可得权向量为

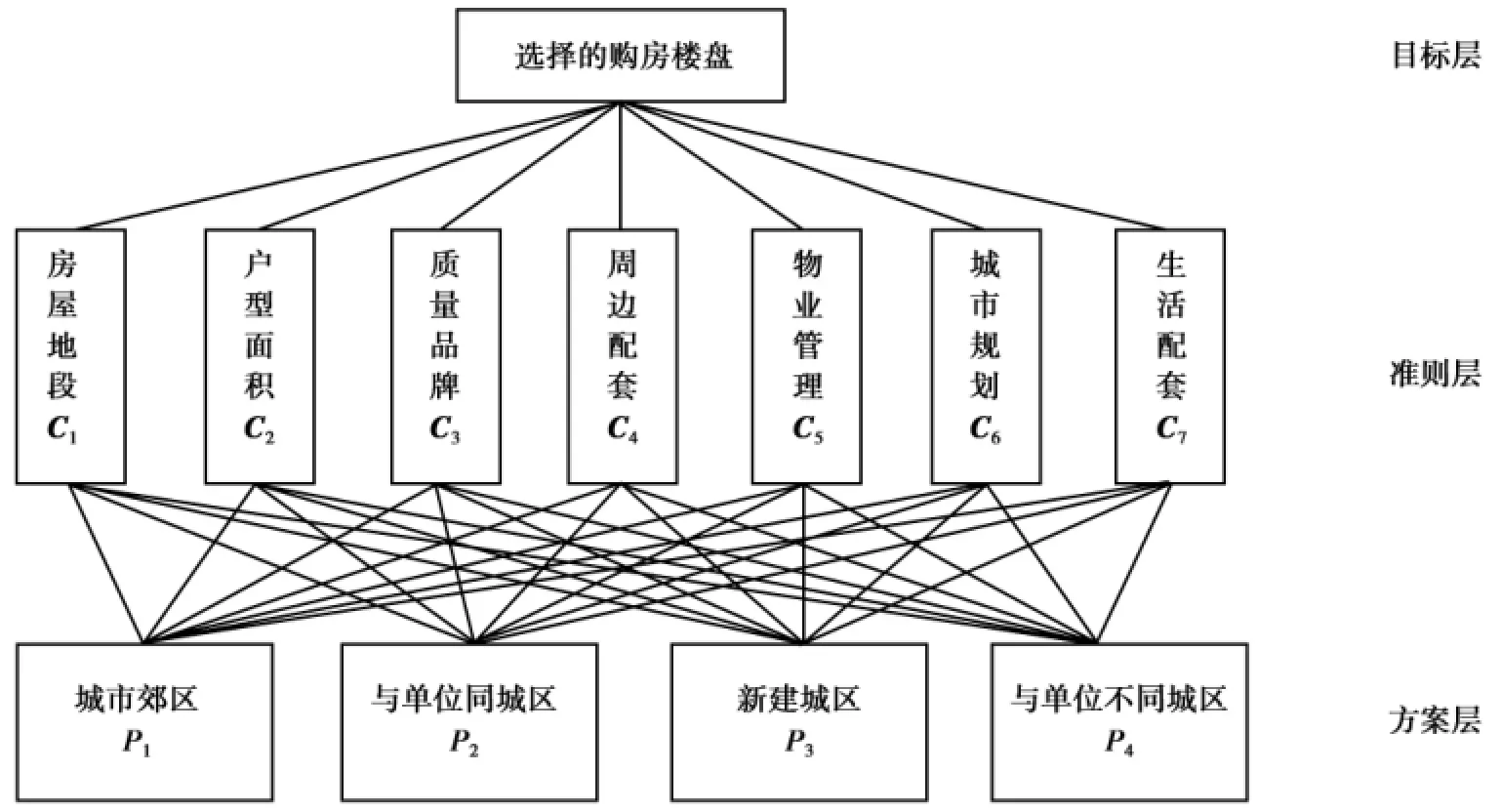
图1 层次结构图

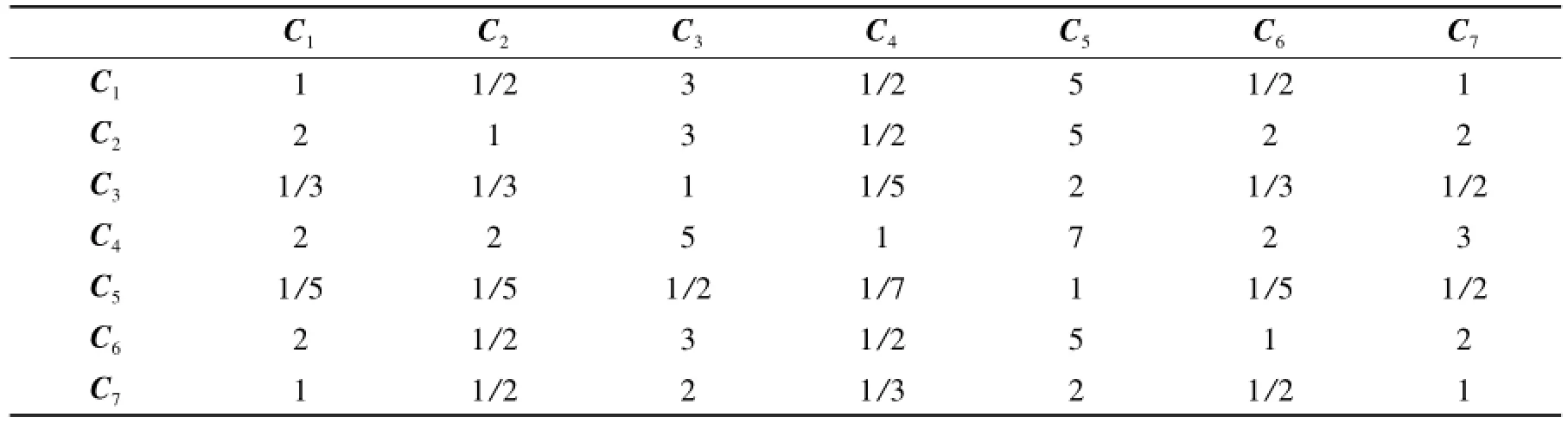
表8 准则层C相对于目标层的成对比较矩阵

2.3 构造方案层对准则层各影响因素的成对比较矩阵

1)针对房屋所处地段C1与方案层的比较结果(表9)．

C1的最大特征值［1，2］为λmax＝4．051 1，由文献［1－5］知:RI＝0．90，所以

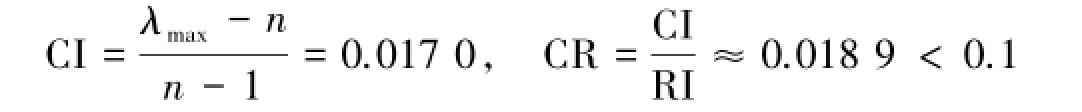
符合一致性检验的要求，是可以接受的．

利用和法［4］可得权向量为

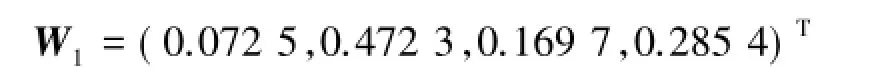
2)针对房屋户型面积C2与方案层的比较结果(表10)．C2的最大特征值为λmax＝4．014 5，由文献［1－5］知RI＝0．90，所以

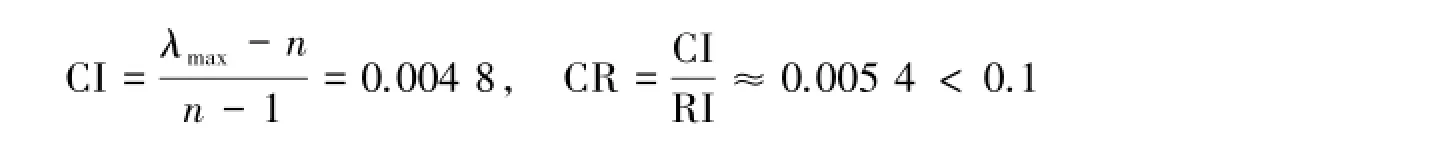
符合一致性检验的要求，是可以接受的．利用和法［4］可得权向量为

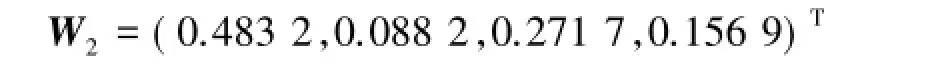
3)针对房屋质量与品牌C3与方案层的比较结果(表11)．C3的最大特征值为λmax＝4．250 6，由文献［1－5］知RI＝0．90，所以

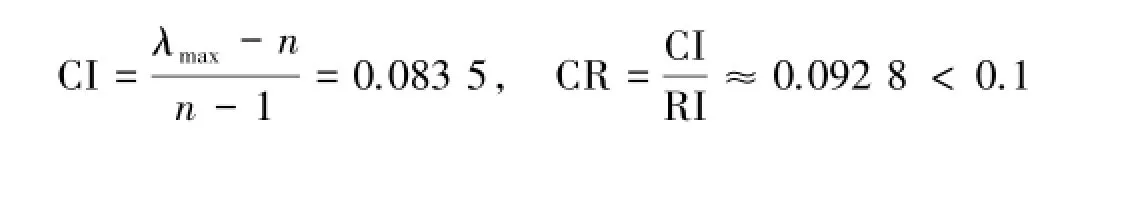
符合一致性检验的要求，是可以接受的.利用和法［4］可得权向量为

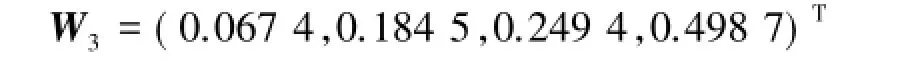
4)针对房屋周边配套设施C4与方案层的比较结果(表12).C4的最大特征值为λmax＝4.0042，由文献［1－5］知RI＝0.90，所以

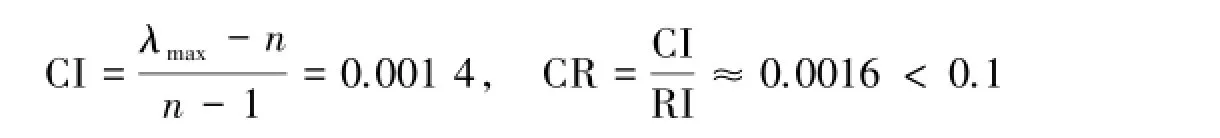
符合一致性检验的要求，是可以接受的.利用和法可得权向量为

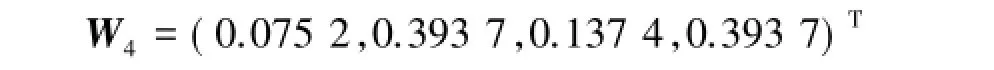
5)针对房屋物业管理C5与方案层的比较结果(表13).C5的最大特征值为λmax＝4.0812，由文献［1－5］知RI＝0.90，所以

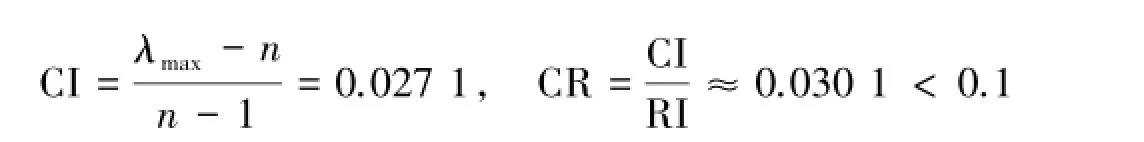
符合一致性检验的要求，是可以接受的.利用和法可得权向量为

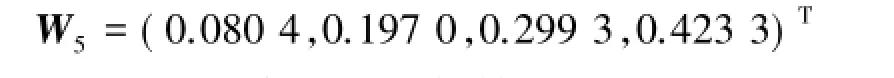
6)针对房屋周边未来城市规划C6与方案层的比较结果(表14).C6的最大特征值为λmax＝4.0206，由文献［1－5］知RI＝0.90，所以

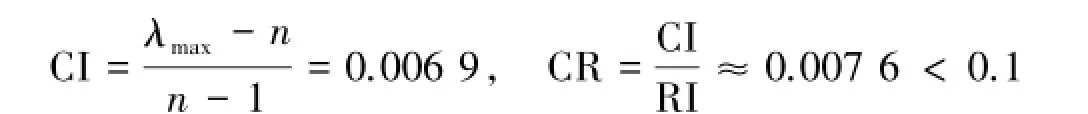
符合一致性检验的要求，是可以接受的.利用和法可得权向量为

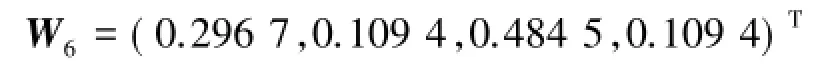
7)针对房屋生活配套设施C7与方案层的比较结果(表15).C6的最大特征值为λmax＝4.0206，由文献［1－5］知RI＝0.90，所以

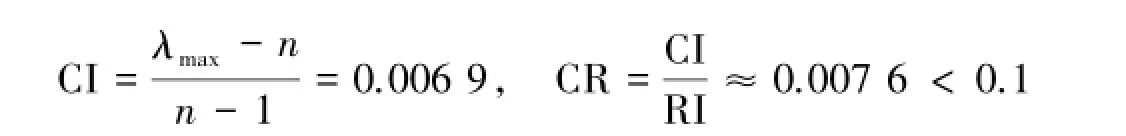
符合一致性检验的要求，是可以接受的.利用和法可得权向量为

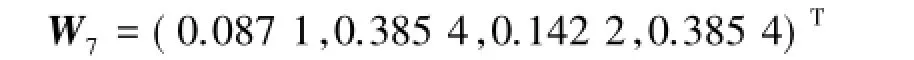
结合以上讨论，用(P1，P2，P3，P4)T表示方案层中4个备选方案在目标层中的比重，依据笔者购房考虑因素的要求，对方案层中个备选方案在目标层中所占比重的计算式［1］为

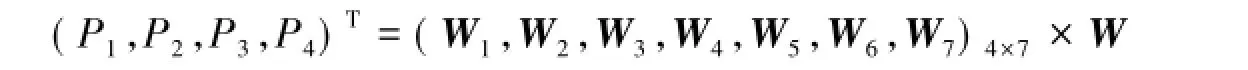
表9 房屋所处地段C1与方案层的比较

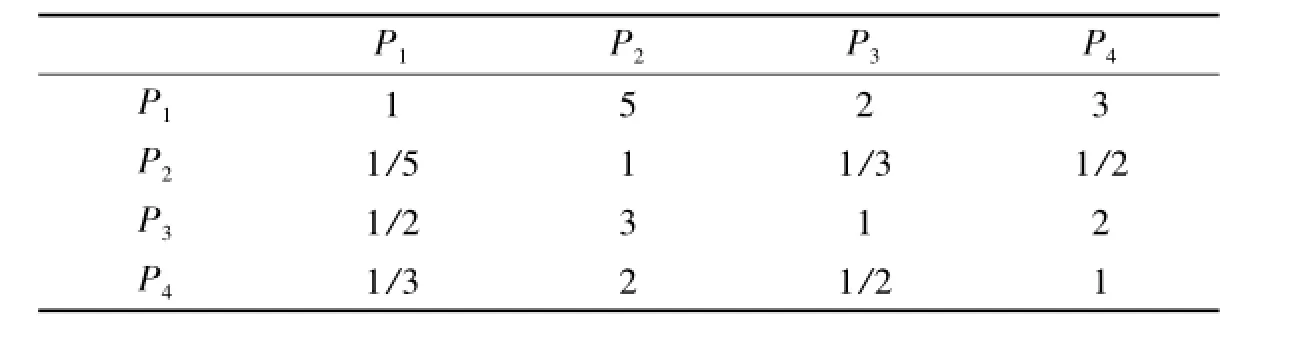
表10 房屋户型面积C2与方案层的比较

表11 房屋所处地段C3与方案层的比较

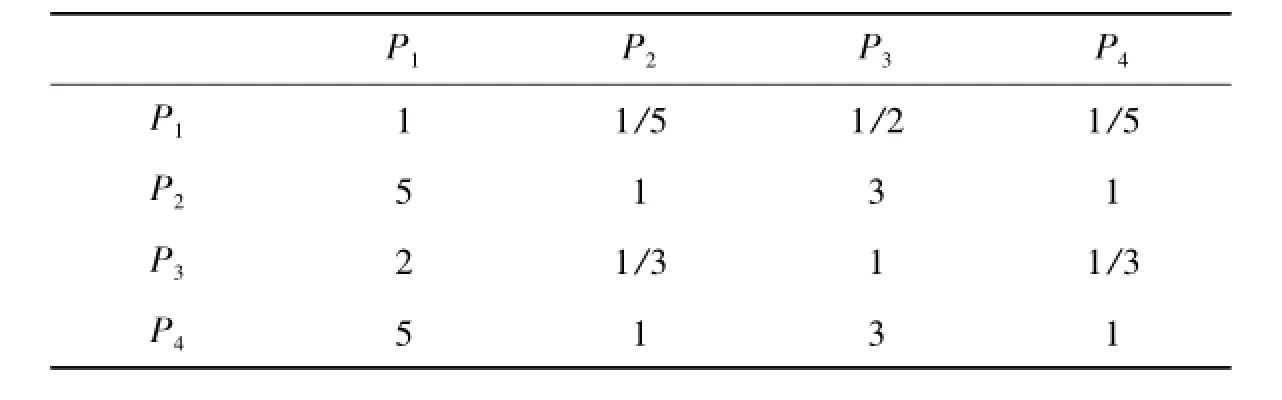
表12 房屋周边配套设施C4与方案层的比较

表14 房屋周边未来城市规划C6与方案层的比较

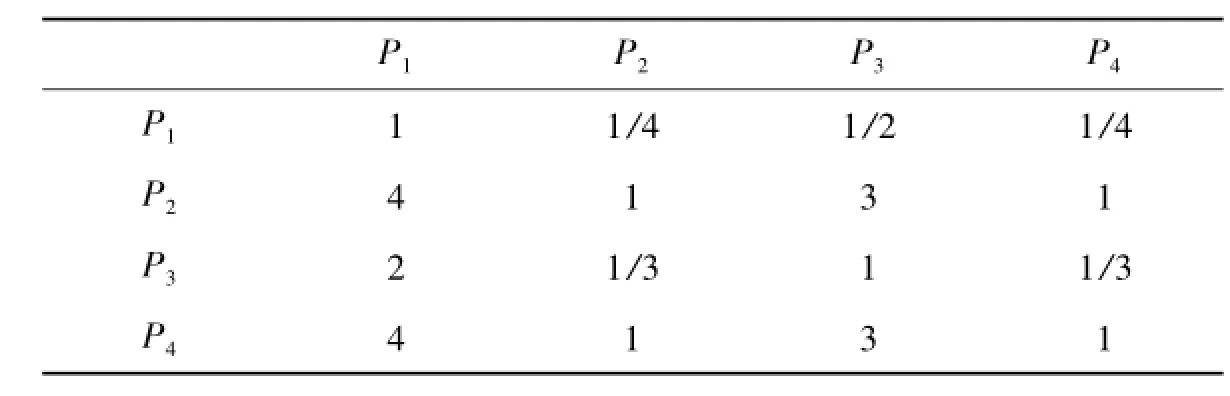
表15 房屋生活配套设施C7与方案层的比较

3 依据购房要求得出综合评价及购房建议

将相关数据代入上述购房决策模型，(P1，P2，P3，P4)T＝(W1，W2，W3，W4，W5，W6，W7)4×7×W可得

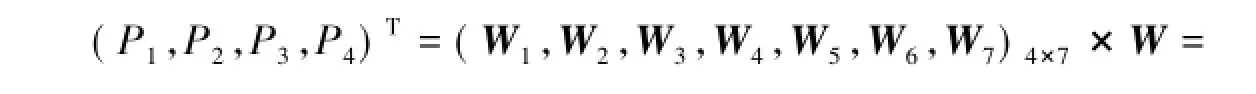
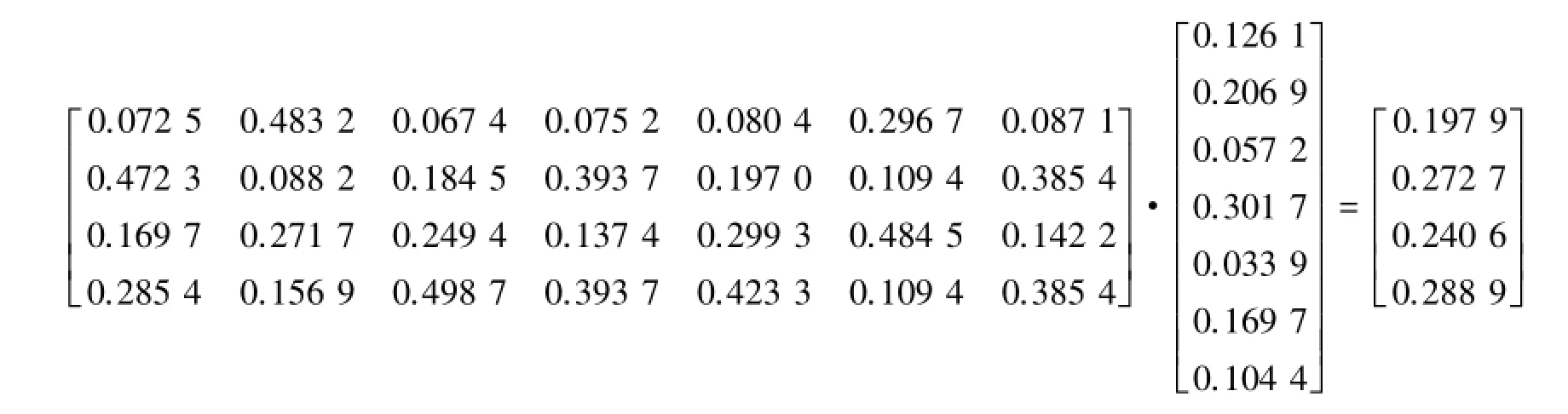
结合以上分析可得，购买城市郊区楼盘P1所占比重为0.1979，购买与工作单位同一城区楼盘P2所占比重为0.2727，购买城市新建城区楼盘P3所占比重为0.2406，购买与工作单位不同城区楼盘P4所占比重为0.2889.

应用层次分析法模型，结合笔者购房的考虑，对这4类在售楼盘可以做下列排序：第一选择与工作单位不同城区楼盘，第二选择与工作单位同一城区楼盘，第三选择购买城市新建城区楼盘，最后选择城市郊区楼盘.

［1］姜启源.数学模型［M］.2版.北京：高等教育出版社，1999

［2］陈义华.数学建模的层次分析法［J］.甘肃工业大学学报，1997，23(3)：92－96

［3］吴祈宗，李有文.层次分析法中矩阵的判断一致性研究［J］.北京理工大学学报，1999(4)：502－505

［4］唐焕文，贺明峰.数学模型引论［M］.3版.北京：高等教育出版社，2005

［5］吴小伟，陈彦，仲崇庆.基于AHP法滨海旅游资源定量评价——以连云港为例［J］.重庆工商大学学报：自然科学版，2013(6)：53－60

Young People’s House Purchasing Model Based on Analytic Hierarchy Process

ZHANG Hua

(Shanxi Architectural College，Taiyuan 030006，China)

In order to solue the problem of difficult decision making on husing purachase for young people，choosing houses of the same initial payment and using analytic hierarchy process，this paper constructs the mathematic model of house purchasing，and solves house purchsing decision problems for young people by quantitative method.

Analytic Hierarchy Process；mathematic model；house purchasing problem；decision

O157.5

A

1672－058X(2015)04－0085－06

10.16055/j.issn.1672－058X.2015.0004.019

2014－09－26；

2014－10－14.

张华(1980－)，男，山西太原人，讲师，硕士，从事应用数学研究.