高职数学课程中学生职业通用能力培养理论的建构与培养模式设计*

金秀岩

(广东松山职业技术学院基础部，广东韶关 512126）

高职数学课程中学生职业通用能力培养理论的建构与培养模式设计*

金秀岩

(广东松山职业技术学院基础部，广东韶关 512126）

在BTEC教学模式理念下，建构了高职数学课程目标与职业通用能力培养目标相融合理论和数学课程教育模式与职业通用能力培养模式相融合的理论，并描述了高职数学课程教育模式与职业通用能力培养模式相融合的基本框架；在该理论的基础上，设计了培养学生职业通用能力的模式以及学生职业通用能力培养的评价体系。

高职数学课程；学生；职业通用能力；培养

BTEC(Business＆Technology Education Council)是英国商业与技术教育委员会的简称，BTEC的教育理念概括起来就是“以能力为本位，以学生为中心”。人们在实际工作中，不仅需要职业技能知识，还需要合作能力、沟通能力、解决问题的能力和创新能力等通用能力。在职业生涯中，通用能力对职业技能的发挥以及个性的发展都有重要的作用，并且当面临就业、晋升、转岗等情况时，能使人们具有更强的竞争力。

BTEC认为培养学生发展专业技能的同时，还应特别重视对学生通用能力的培养，使学生成为岗位适应性强和积极上进的高素质劳动者。BTEC将学生应具备的通用能力归纳为自我管理和发展能力、合作能力、交往沟通能力、安排任务和解决问题能力、数字运用能力、科技应用能力、设计与创新能力等7个领域，并把通用能力的培养目标落实在所有课程的教学活动中，有计划、有步骤地培养学生。

BTEC教学模式理念中，将专业技能和通用能力的培养放在同等重要的位置上，并力求将通用能力的培养落到实处。在设计课业时，教师除说明完成的教学目标外，还要说明本课业要发展学生哪些领域的通用能力及获得哪些成果，在评估学生课业时，应特别注意评估通用能力的成果。

目前，关于BTEC教学模式的研究成果比较多，但多数局限在专业课或专业群，很少在数学课程的层面进行研究。众所周知，数学课程是高职院校各专业的公共基础课，作用主要表现在工具性和服务性上。然而数学课程在培养学生职业通用能力中的重要作用而被忽视了。因此，有必要探索高职数学课程中学生职业通用能力培养理论，来丰富和发展高职数学教育的理论和作用。特别是目前我国面临产业转移和产业升级的关键时期，对高职毕业生，不仅在知识、技能水平方面有较高的要求，而且要求能够应变和发展。为此，高职院校在培养学生职业技能的同时，应注重学生的职业通用能力的培养，这样才能使学生更好地适应未来社会发展需要。

1 相关概念的界定和研究方法、研究范围

1.1 相关概念的界定

“数学课程是指数学教学科目，以及在数学教学大纲(数学课程标准)和数学教材系列中所规定的数学教学的目的、内容、范围、分量和进程的总合［1］。”高职数学课程是指高等职业教育中适应培养生产、建设、管理、服务第一线所需要的高等技术应用性专门人才所设置的数学课程。

BTEC认为，职业通用能力是一种可迁移的、从事任何职业都必不可少的跨职业的关键性能力。因此，界定高职学生的职业通用能力为具备高等职业教育特点的，并为学生职业技能的提升和发展，适应转变角色，新的工作环境以及可持续发展提供必要基础的基本职业通用能力。

1.2 研究方法和研究范围

运用文献分析法，在高职数学课程的教育教学范围内，在BTEC教学模式理念下建构学生职业通用能力培养理论。在该理论的基础上，设计培养学生职业通用能力的模式以及评价体系。

2 学生职业通用能力培养理论的建构

2.1 课程目标与职业通用能力培养目标相融合理论

2.1.1 基本思想

高职数学课程目标应与职业通用能力培养目标相融合，与人才培养目标、人才培养层次以及社会对人才能力要求相适应。据此，提出高职数学课程目标与职业通用能力培养目标相融合的理论假设：以BTEC教学模式为基础，构建高职数学课程目标↔职业通用能力培养目标↔人才培养目标交互作用的理想理论模型，并将其作为培养学生职业通用能力的理论背景和方法论。

这两种目标要在相互支撑、相互补充、相互促进下，为有效提高学生的综合素质和能力承担起重要作用；要在实现高职数学课程目标的过程中，有目的、有计划、有组织地实现培养学生职业通用能力的目标；要在培养学生职业通用能力的过程中，有目的、有步骤、有意识地开展数学教学活动。

为了充分挖掘高职数学课程在培养高技能应用性专门人才中的功能，此处将高职数学课程的主要功能概括提炼为基础服务性和职业通用能力培养等两个方面。其中，基础服务性就是为学生顺利完成专业基础课和专业课程的理论知识的学习提供必要的数学基础和数学素养，为学生更好地学习新技能、新技术，提高创新能力以及可持续发展提供必要的数学能力；职业通用能力培养就是在数学课程目标和教学计划的制定、教学组织以及学业考核等方面，注重培养学生的职业通用能力，使数学课程目标的实现成为高职教育中人才培养的重要组成部分，在数学课程与职业通用能力培养之间搭建有效桥梁，使学生在学习数学的过程中得到职业通用能力的培养。

2.1.2 基本框架

高职数学课程目标与职业通用能力培养目标相融合，包括数学课程内容与职业通用能力的内涵的融合、数学学习特点与职业通用能力培养特点的融合、数学学习方法与职业通用能力培养要求的融合等，其中以数学课程内容与职业通用能力的内涵的融合为核心，组成集数学教育与职业通用能力培养于一体的高职数学教育教学模式，达到在数学教学中培养学生的职业通用能力的目的。

2.2 高职数学课程教育模式与职业通用能力培养模式相融合理论

2.2.1 基本思想

高职数学课程教育模式与职业通用能力培养模式相融合的关键是高职数学课程体系与职业通用能力培养体系的融合。据此提出高职数学课程教育模式与职业通用能力培养模式相融合理论假设：以人才培养层次为基础，构建高职数学课程体系↔人才培养层次要求↔职业通用能力培养体系交互作用的理想理论模型。

这两种模式之间相互支撑、相互补充、互相促进，是相辅相成的，在实现数学教育的过程中完成职业通用能力的培养，在职业通用能力的培养过程中完成数学教育的任务。在BTEC教学模式下，根据人才培养层次的具体要求和高职数学课程的实际特点，构建职业通用能力的培养模式，使之与数学教学规律、数学学习方法之间形成密切衔接。数学课程教育模式要在充分考虑培养职业通用能力培养要求的基础上，以兼顾数学特有的教学规律和学习方法的基础上，充分考虑培养职业通用能力培养要求，创设符合培养职业通用能力教学环境，使之与职业通用能力的培养有效融合。

2.2.2 基本框架

高职数学课程教育模式与职业通用能力培养模式相融合，包括数学教学目标与职业通用能力培养目标的融合、数学教学程序与职业通用能力培养程序的融合、数学教学的实现条件与职业通用能力培养要求的融合、数学课程的评价与职业通用能力的评价融合等4个方面。这4个方面要以实现数学教学目标和职业通用能力培养目标为核心，形成一个相互支撑的有机整体。

3 学生职业通用能力培养模式的设计

3.1 设计培养模式的依据

高等教育心理学依据。布鲁纳(J.S.Bruner)和舒赫曼(R.Suchman)认为，学生本能地对一切新奇的事物感兴趣，这种自发的好奇心促使人们在面对陌生现象时尽力寻找其发生的原因。教师在教学过程的作用是，积极为学生创设问题情境，鼓励学生自己提出问题、分析问题、提出假设并最终解决问题［2］。因此，构建培养模式时，注重设置引发学生兴趣和好奇心的情境，创建相对自由发挥的学习空间，调动学生自主学习和合作探索积极性，培养学生分析问题、解决问题的能力。

数学教育学依据。当代数学教学模式的基本特点是：以发展学生的智能为基点，突出教学的发展性；以学生的学习为中心，充分调动学生学习的主动性和积极性，突出教学的多边性；发挥非智力因素的作用，注重教学的情感性；优化组合教学方法，突出教学的综合性；把实验探索与理性思维训练结合起来等［3］。因此，构建培养模式时，要从实际中提出问题，并以多角度、多情景以及课内外相结合的方式，积极调动学生的参与意识和自主探索意识，促进数学教学质量和职业通用能力的提高。

问题中心课程论依据。根据问题中心课程理论，在高职数学课程中学生职业通用能力培养模式的构建中，以解决社会以及专业技能等实际问题为核心，以培养学生职业通用能力为目标，既强调内容，又强调学生的兴趣与活动，从问题出发，把社会需要、专业技能以及数学课程结合起来。

社会学理论依据。当代德国著名的社会学家哈贝马斯(Habermas)的“沟通行动理论”认为“从相互理解的角度来看，沟通行为是用来传播和更新文化知识的；从协调行为的角度来看，沟通行为起着社会整体化和创造团结互助的功能；最后，从社会化的角度的看，沟通行为是为了造成个人的独有的特征和本质。”由此可见，社会、文化、道德、理性及个性等一切重要社会问题都离不开沟通行动。为此，构建培养模式时，要注重学生在参与社会实践的过程中，通过各种有效沟通方式收集、整理、加工信息的环节的设计。

此外，培养模式的设计也是高职教育人才培养需要，辅佐专业教育的需要，数学学习方法的需要。

3.2 学生职业通用能力培养模式设计过程

3.2.1 设计目的

在BTEC教学模式理念下，将职业通用能力培养要素合理融入到数学教育教学的整个过程之中，培养具有沉着面对知识、技能、岗位种类变化，并能够获得新知识、新技能，善于应变和发展自己创新能力的高素质人才。

3.2.2 设计原则

(1)相融性原则。数学课程内容的设置上，根据课程特点将培养职业通用能力的因素融于其中，做到在讲授数学、学习数学的过程中培养学生的职业通用能力。

(2)适应性原则。数学课程的内容、教学组织形式、学习方式方法要适应培养学生职业通用能力的要求；适应高职学生学习专业知识和专业技能的要求；适应学生不断更新知识、技能和发展的需要。

(3)灵活性原则。数学课程的教学形式，根据培养职业通用能力的需要和学生的实际情况，结合专业特点采取灵活多样、丰富多彩的教学形式，促进学生的职业通用能力的形成。

(4)服务性原则。数学课程的内容要服务于高技能人才培养的需要，服务于学习专业课程与专业技能的需要，服务于学生可持续发展的需要。

3.2.3 模式的设计

(1)高职数学课程的设置。以学校人才培养方案为指导，根据职业通用能力培养要求充分考虑不同专业对数学知识的需要，合理设置数学课程。将数学课程内容分成若干个模块，供不同专业或专业群根据人才培养需求选用不同的模块，以增强数学课程的针对性和实效性，以我院电气系各专业为例，根据专业特点和人才培养需要设置了4个数学课程模块，分别是微积分、线性代数、傅立叶变换、MATLAB软件应用；微积分、线性代数、拉普拉斯变换、MATLAB软件应用；微积分、概率论、傅立叶变换、MATLAB软件应用；微积分、线性代数、MATLAB软件应用。

(2)教学组织形式。按照相融性、适应性、灵活性、服务性的原则，把BTEC职业通用能力的自我管理和发展、与他人合作共事、交往和联系、安排任务和解决问题、数字应用、科技应用、设计和创新等7个领域的内涵，分类嵌入到数学教学的每个环节之中，使数学教学与培养学生职业通用能力同步进行。

根据数学课程内容、特点以及培养职业通用能力的需要，以“首要教学原理［4］”为理论依据，实行“以问题为中心”的教学组织形式，以实践教学作为辅助教学手段，激发学生的学习兴趣和积极性，促进教学效果的提高。首要教学原理包括问题中心、激活、展示、应用、整合等5项教学原理，强调教学应该以问题为中心，而其他4项原理是对应有效教学4个阶段的。其主要教学组织形式分以下几种：

①引导探究形式，一般适用于培养职业通用能力之数字应用、设计和创新，获得多样性的技能来适应新环境。即学生在教师的引导下，根据实例分析，探究相关数学规律，利用已有的知识尝试性地定义新概念或得到新结论(定理)，获得新知识，以实现教学目的。其教学结构是创设情景——提出问题——探究规律——总结归纳——得到结论。

②协同操作形式，一般适用于培养职业通用能力之与他人合作共事、交往和联系。即根据教学内容的安排，将学生分成若干个由8～10人组成的学习小组，通过互相交流、讨论，协同完成学习任务，共同获得知识，达到教学目的。其教学结构是提出问题——协同合作——讨论交流——获得知识。

③合作实践形式，一般适应于培养职业通用能力之自我管理和发展。即以课外数学建模竞赛、数学兴趣小组、生产实训的形式，为学生营造自主学习、自主收集信息、自由探索、自由发现的教学情景，使学生在实践和探索中获得知识，实现教学目的。其教学结构是提出问题——分工收集信息——讨论交流——优化方法——得到结论。

3.3 学生职业通用能力培养的评价

3.3.1 评价目的

评价是为了诊断和检验所建立的“高职数学课程中学生职业通用能力培养模式(以下简称“模式”)”的实施效果，适时调节和控制实施过程，使“模式”的实施效果得到最优化，促使“模式”有效运行，使广大学生达到掌握数学知识，提高职业通用能力的目的。

3.3.2 评价原则

(1)科学性原则。遵循教育规律，以科学、实事求是、客观公正的态度，制定评价指标和评价方法，并用合理的手段进行评价。

(2)可行性原则。评价标准体现全面客观具有代表性，评价方法科学合理具有可操作性，评价结果可信度高，有利于指导“模式”的改进与升级。

(3)普遍性原则。评价对象和结果具有一定的普遍性，能够比较全面反映客观事物的普遍特点。(4)客观性原则。评价结果和过程都应该符合客观实际，尊重客观事实，事实求是。

3.3.3 评价指标体系的建立及评价方法

(1)评价指标体系建立。以BTEC职业通用能力的内涵作为评价学生职业通用能力的因素，建立多层次结构指标体系(表1)。

表1 学生职业通用能力评价指标层次结构

由表1知，评价指标体系分为3个层次，第一层为目标层，只有1个指标A；第二层为准则层，有7个指标P＝(P1，P2，P3，P4，P5，P6，P7)；第三层为指标层，分7组，分别对应准则层的7个指标集。

(2)评价方法。

①数据采集办法。在教学实践过程中，施教者或管理者(教师、辅导员、指导教师)对每个学生填写《学生职业通用能力评价表》(见表2)，评价时对相应项目的表现只作优、良、中、一般、差5个等级的评定。

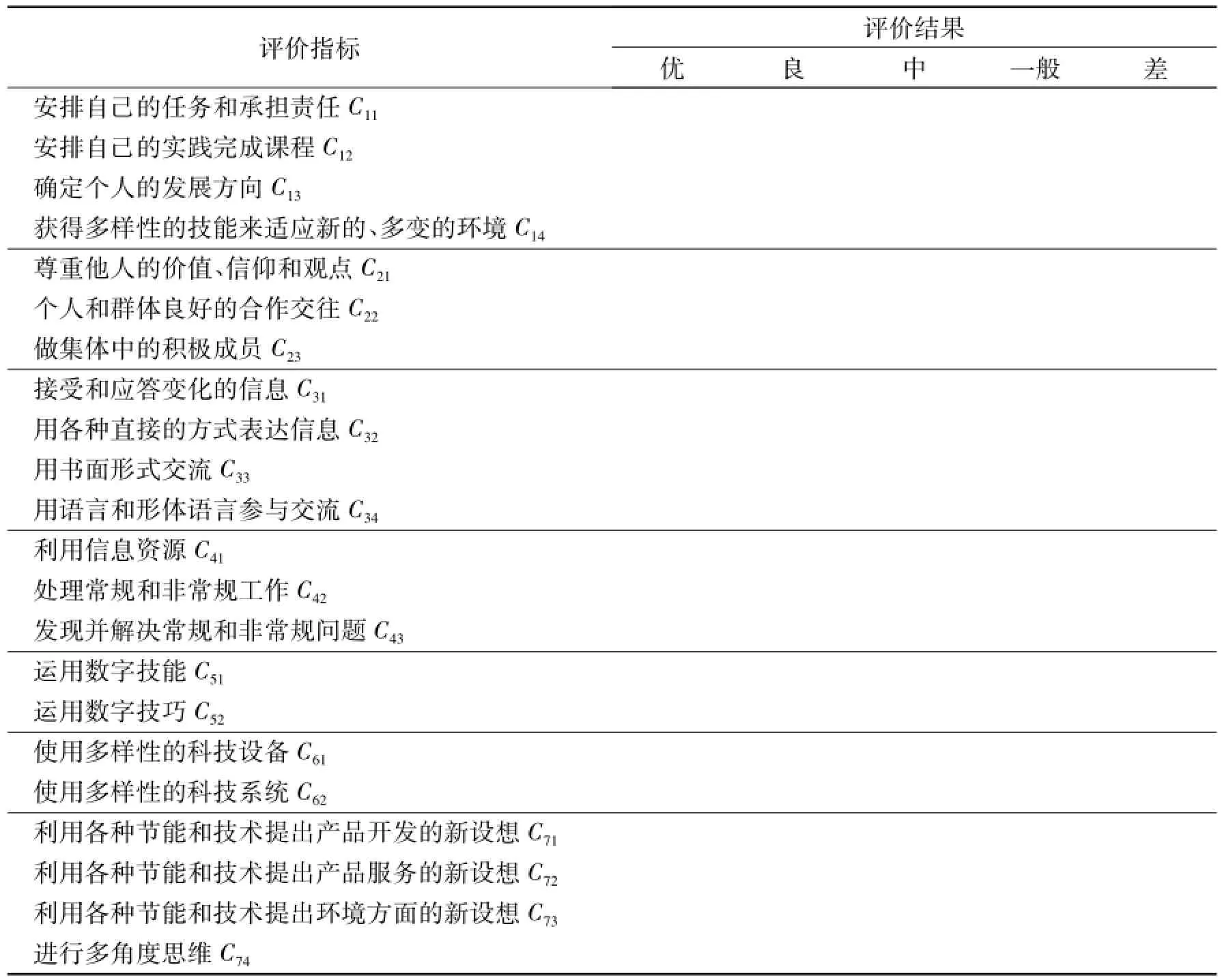
表2 学生职业通用能力评价表

②研究方法的选择与数据处理方法。研究方法的选择。由上述评价指标体系不难看出，当给被测试者评价结果时，很难用具体的量化指标予以评价，更多的是比较模糊的、非确定性的评价。而模糊综合评价法是一种基于模糊数学的综合评标方法，它具有结果清晰，系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决。因此，选用模糊综合评价法评价是取得相对客观公正、公平结果的好办法。

数据处理方法及结果。根据表1建立的二级模糊综合评判模型，并由表2所获得的相关数据对被测评者予以综合评价。具体办法是：

1)分别设立各层指标对应于上一级指标的权重向量。权重向量的计算，根据职业通用能力内涵的实际意义，认为每个评价指标对上一级指标同等重要，故权重是均等的。于是，可以设准则层P对应于目标层A的权重向量WP＝(1/7，1/7，1/7，1/7，1/7，1/7，1/7)；指标层C对应于准则层P的权重向量分别为

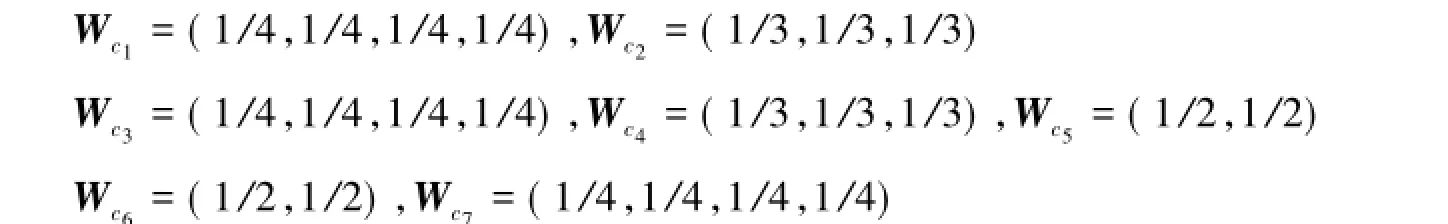
2)确定评价等级的加权向量。对每一指标设立一组模糊评价值：优、良、中、一般、差，评价集合记为V＝{v1，v2，v3，v4，v5}，评价等级的加权向量是评价等级在不考虑模糊边界条件下的值，反映的是各个评价对最终结果的影响程度，一般采用百分制。如评价集V的权重可取为V＝{96，80，70，60，40}。

3)根据评价标准和指标体系形成各级指标集的评价矩阵和各指标的评价向量。首先，建立指标Cij的评价向量和指标集Ci的评价矩阵。在评价集V上对第三指标层中的每一个指标Cij作评价，其中评价为优、良、中、一般、差的数量分别为由此得每一个指标Cij评价向量Rij＝再由评价向量Rij作为行向量分别构造该指标集Ci(i＝1，2，3，4，5，6，7)的评价矩阵R1＝(R11，R12，R13，R14)T，R2＝(R21，R22，R23)T，R3＝(R31，R32，R33，R34)T，R4＝(R41，R42，R43)T，R5＝(R51，R52)T，R6＝(R61，R62)T，R7＝(R71，R72，R73，R74)T。

其次，建立指标Pi的评价向量和指标集P的评价矩阵。评价矩阵Ri(i＝1，2，3，4，5，6，7)与对应指标集的权重向Wci(i＝1，2，3，4，5，6，7)相乘，可计算出上一级指标Pi(i＝1，2，3，4，5，6，7)的评价向量，即指标Pi(i＝1，2，3，4，5，6，7)的评价向量为Di＝Wci·Ri(i＝1，2，3，4，5，6，7).由Di(i＝1，2，3，4，5，6，7)构造指标集P的评价矩阵D＝(D1，D2，D3，D4，D5，D6，D7)T。

再次，建立指标A的评价向量。指标集P的评价矩阵与其权重向量WP的乘积即为指标A的评价向量H＝WP·D。

最后，根据各指标的评价向量和评价等级的加权向量V得到各指标的评价值。

目标层(职业通用能力)A的综合评价值：

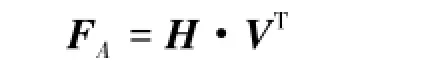
准则层(有7个指标)Pi的评价值：

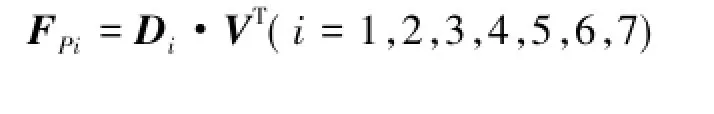
［1］田万海.数学教育学［M］.杭州：浙江教育出版社，1993

［2］教育部人事司.高等教育心理学［M］.北京：高等教育出版社，1999

［3］周春荔，张景斌.数学学科教育学［M］.北京：首都师范大学出版社，2001

［4］DAVIDM.首要教学原理［J］.盛群力，马兰，译.远程教育杂志，2003(4)：20－27

Construction of Student Vocational General Ability Training Theory and Its Training Mode Design in Higher Vocational Math Course

JIN Xiu-yan

(Department of Basic Courses，Guangdong Songshan Polytechnic College，Shaoguan 512126，China)

For high vocational colleges，teaching mode of BTEC constructs the theory of converging mathematics curriculum objectives and vocation general abilities training objectives and the theory of integrating mathematics course teaching mode and vocation general abilities training mode，describing the basic framework of mathematics course in Higher Vocational Education and the general vocational abilities training mode in combination.Based on this theory，this paper designs student vocational general abilities training mode and its evaluation system.

Mathematics curriculum in higher vocational colleges；student；vocational general abilities；training

G714

A

1672－058X(2015)04－0097－08

10.16055/j.issn.1672－058X.2015.0004.021

2014－08－16；

2014－09－25.

*课题项目：广东省教育科研“十二五”规划2012年度研究项目(2012JK124)；广东松山职业技术学院教科研项目(2012－JKYX－6).

金秀岩(1961－)，朝鲜族，男，吉林人，副教授，从事数学课程教学论和概率统计研究.