SVM与组合矩在工件识别中的应用研究*

周伟峰，江娟娟，林园胜，许钢

(安徽工程大学安徽省检测技术与节能装置省级实验室，安徽芜湖 241000）

SVM与组合矩在工件识别中的应用研究*

周伟峰，江娟娟，林园胜，许钢

(安徽工程大学安徽省检测技术与节能装置省级实验室，安徽芜湖 241000）

针对工件识别问题，提出了一种应用支持向量机(Support Vector Machine，SVM)与组合矩对工件进行识别的方法；通过对提取图像的Hu不变矩进行处理，形成利用组合矩进行工件识别的新方法；改进后的算法降低了特征维数，缩减了识别时间，提高了识别准确率；结合试验比较了两种方法的分类效果，其中提取Hu不变矩作为特征的识别率为82.3%，而采用组合矩作为特征的识别率高达94.1%，高于Hu不变矩作为特征的识别率.

SVM；Hu不变矩；组合矩；工件分类

目前，图像识别技术在科技的带动下，取得了较快的发展，已广泛应用在工业生产过程中，解决了产品质量合格率不高，生产效率较低的问题.工件识别就是其中的主要应用领域之一.为了提高工件识别的效率，首先要求提取的工件特征具有较强的稳定性，具体体现在旋转(Rotate)、比例(Scale)和平移(Translation)不变性，简称RST不变性.Hu［1］在1962年提出的Hu不变矩即七阶矩就具有RST不变性，目前已应用在工业生产领域.但Hu不变矩提取的特征维数较高，识别过程中增加了识别时间和解决问题的复杂度.此处对Hu不变矩进行组合改进形成组合矩，通过对得到的组合矩进行处理，有效解决了上述存在问题.要解决的实际问题是对工件进行识别分类，由于其特征比较特殊，普通的分类器不能很好地进行识别，而SVM分类器能很好地解决此类问题，对样本有一定的适应性，所以选择SVM作为分类器.

1 工件识别分类流程

基于SVM和组合矩的工件识别和分类流程如图1所示.首先采集工件的图像信息，得到工件的真彩色图像；然后对图像进行灰度化处理；灰度化处理之后采用自适应阈值法进行二值化处理；由于Matlab的前景认定习惯，需要对二值图像进行反二值化，在前面的处理过程中会由于噪声等因素的影响，二值化图像会存在空洞等不良点，因此需要进行闭操作来修补这些狭窄的间断点；之后计算7个不变矩和组合矩特征，得到能够反映工件本身的特征向量把得到的特征向量送入SVM进行训练，得到能够识别工件的SVM分类器；最后用训练好的SVM分类器对工件进行识别分类.

图1 工件识别和分类流程

2 改进组合矩

2.1 Hu矩

Hu矩是1962年由Hu首先提出的，提取的是图像的形态特征，由于其具有RST不变性，所以被广泛应用在图像识别领域.根据参考文献［2］知，对于大小为M×N的数字图像f(i，j)，此幅图像(p+q)的阶矩定义为

式(1)中，f(i，j)相当于一个像素的质量；Mpq为不同p，q值下的图像的矩.基于Mpq的平移不变性，可知p+q阶中心距为

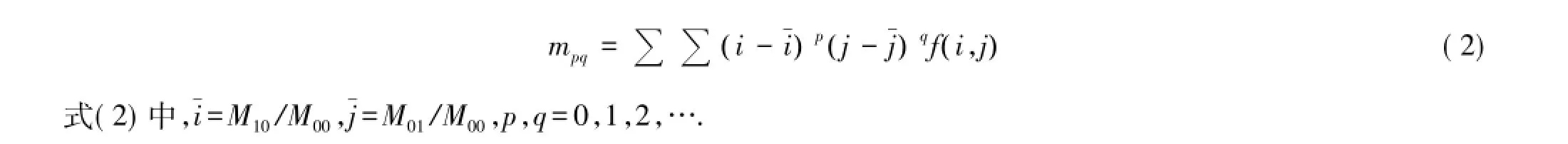
定义归一化中心矩为

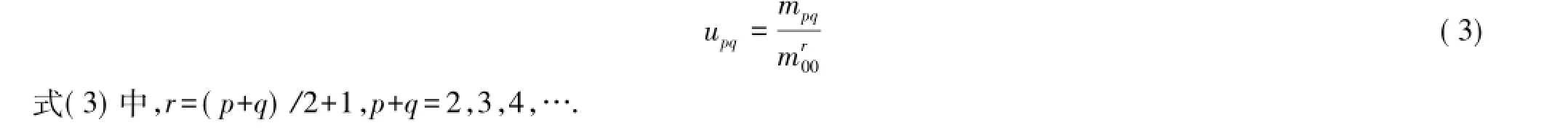
结合归一化中心矩，可以获得利用upq表示的7个不变矩(注意，φ7只具有比例和平移不变性)，表达式如下：

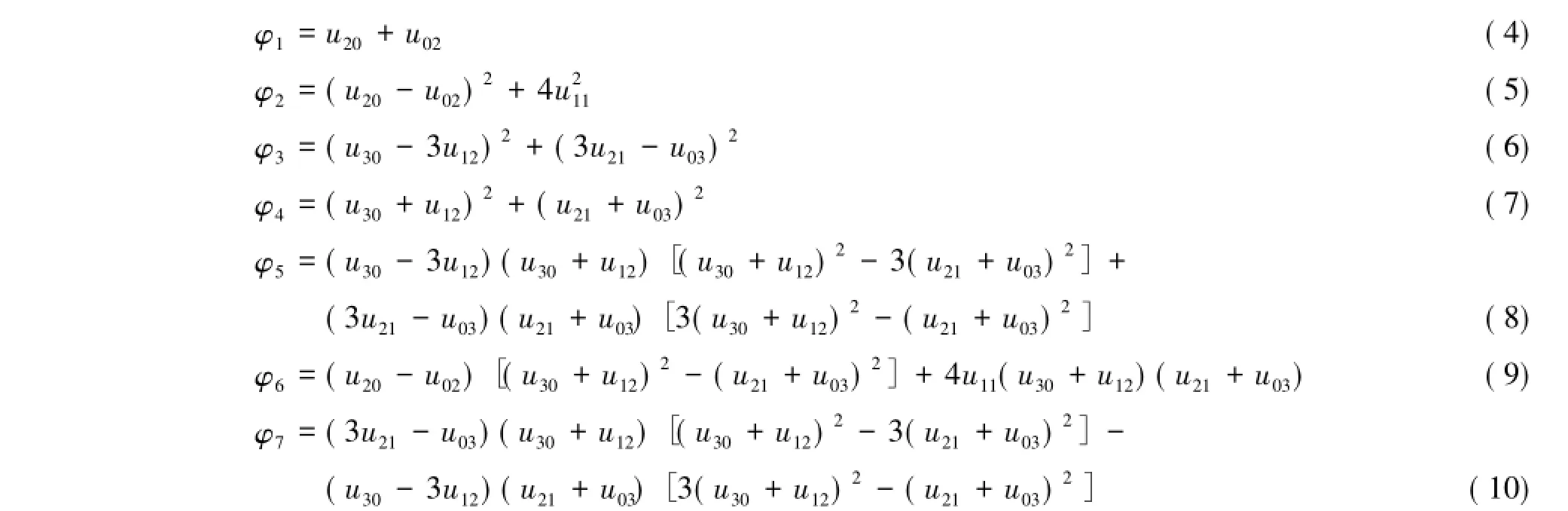
2.2 改进组合矩

由以上推导可知，Hu不变矩主要的表现形式有7种，在提取其作为特征进行识别分类时，由于特征维数较高，导致识别时间长，运算复杂度大.故此处提出将第1，2阶矩组合为φ12组合矩，第3，4阶矩组合为φ34组合矩，第5，6阶矩组合为φ56组合矩，忽略第7阶矩φ7的识别方法(因为第7阶矩只具有比例和平移不变性)，定义为φ12＝φ1+φ2；φ34＝φ3+φ4；φ56＝φ5+φ6.

利用组合矩提取的特征在本质上仍然反映工件的纹理形态，同时增大了特征之间的区分度，不仅具有RST不变性，而且降低了特征维数，缩减了识别时间，进一步的实验证明识别率也有较大提升.

3 支持向量机

支持向量机是建立在统计学习理论基础上的一种优秀的分类算法，是1995年Vapnik［3］提出的.其分类的核心思想是在需要分类的样本中找出一个最优分类超平面，使得需要分类的样本之间具有最大的分类间隔.

3.1 最优分类超平面

SVM最优分类超平面如图2所示，H就是需要找的超平面，在H1和H2上的点就是规定的支持向量.目的就是寻找这样一个超平面H，使得H1和H2之间的间隔最大.

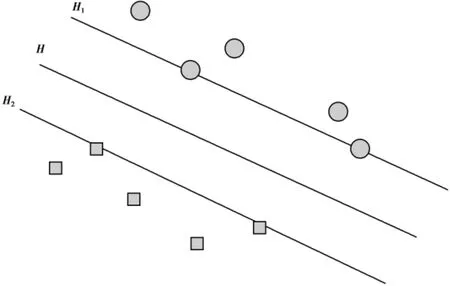
图2 SVM分类超平面

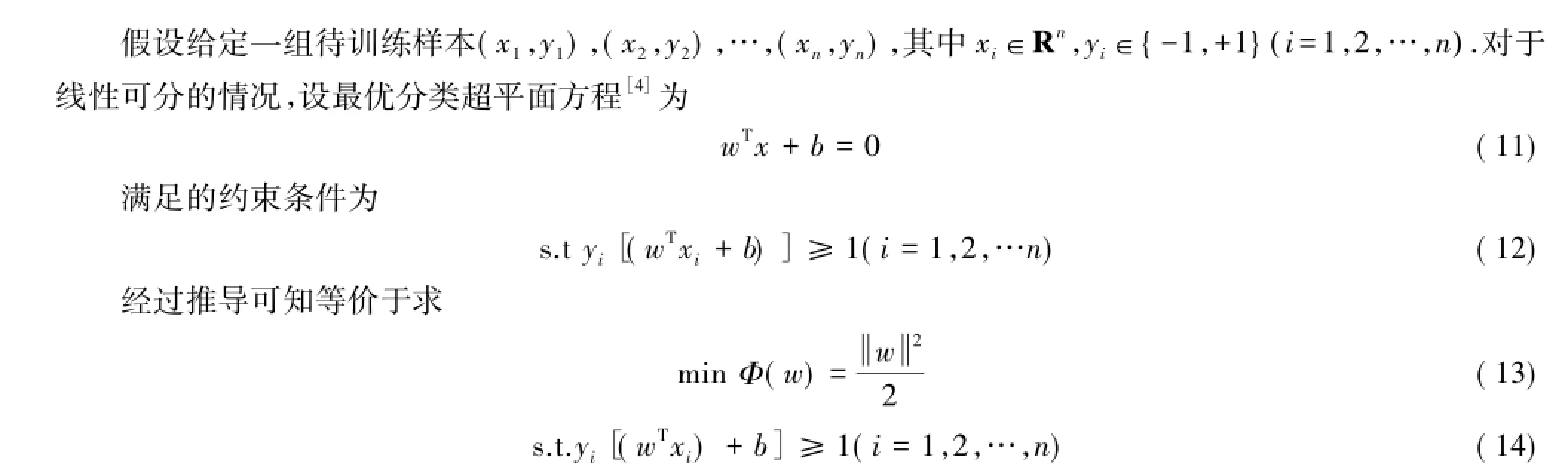
通过对式(13)(14)引进拉格朗日函数，然后对所得拉格朗日函数进行求偏导，把得到的结果带入方程(11)得式(15)

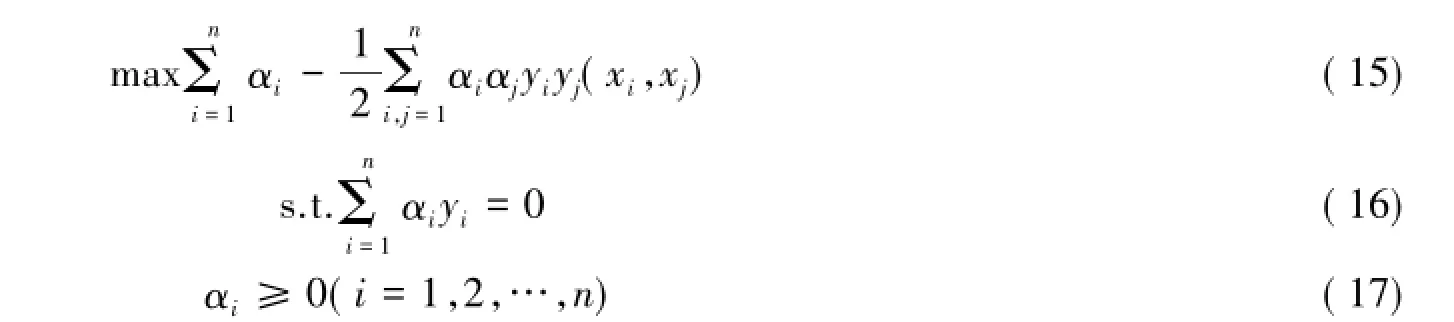
根据式(15)(16)(17)可以解得α，然后带入相应的关系式可得w和b，设相应的最优解为α*，w*，b*，可得最优分类函数

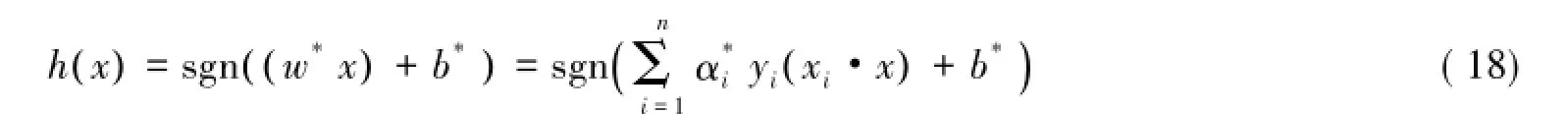
对于非线性情况下的SVM分类，通过引进松弛变量εi＞0，得约束条件为

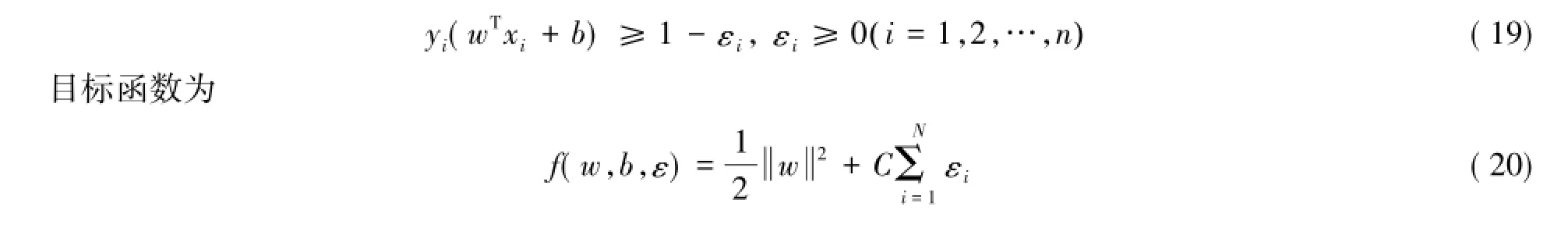
通过对式(20)引进拉格朗日函数、求偏导、解方程可知，最后求得的最优解和线性可分情况下的最优解α*，w*，b*是一致的.

3.2 构造核函数SVM

在非线性可分的情况下，通过引进函数ψ( x)，把样本映射到高维空间中，使得在高维空间中样本线性可分.通过和线性分类类似的推导，可得目标函数［4］为

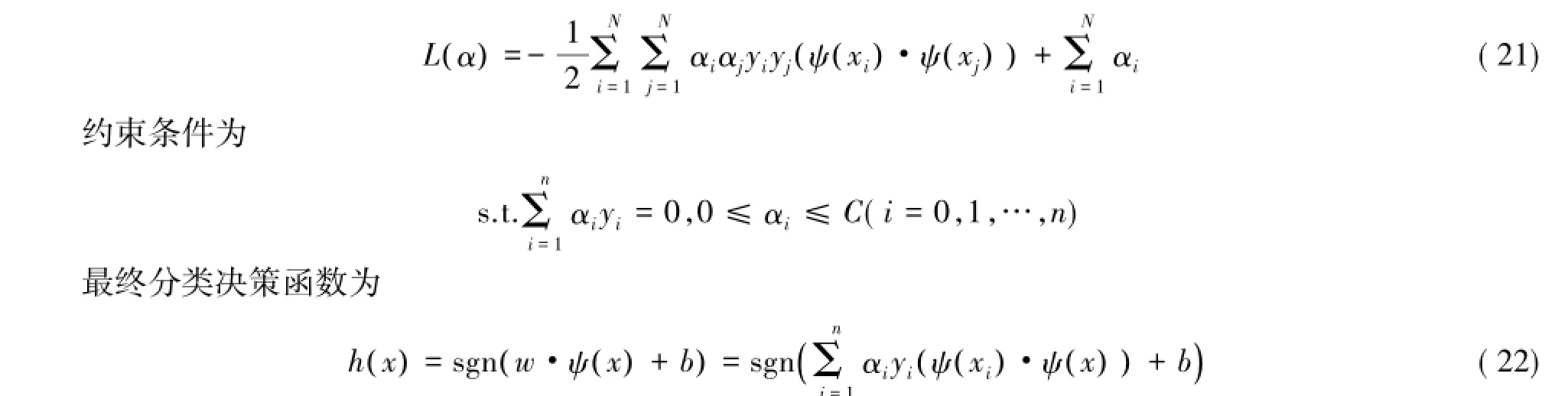
实际上在计算点积ψ (xi)·ψ (xj)时可以用一个核函数K (xi，xj)代替，从而把低维空间的样本映射到高维空间.这种替换并没有增加运算的复杂度，反而使问题的求解更加方便.由此可知构造的决策函数为

3.3 核函数［5］

不同的核函数可以构造出不同的SVM分类器，不同的分类器则形成了不同的分类结果，所以核函数的选择非常重要，是决定分类器性能好坏的主要参数之一.目前主要的核函数［6］有多项式核函数为K(x，xi)= (xxi+1)d；径向基函数为K(x，xi)=exp{－g x－xi2}；两层感知器为K(x，xi)=S(v(x，xi)+c)，其中，S是Sigmiod函数，v，c为常数.通过实验对比各个核函数的优缺点，可知径向基核函数具有很好的分类效果，最终选择了径向基核函数来解决此类问题.

3.4SVM多类分类方法

支持向量机主要解决的是二分类问题，对于多类问题，需要结合多个二分类器对样本进行分类，主要有以下几种分类方法：

1)一对多分类器.把所有样本分为两大类，其中某一个样本为一类，另外一些样本为另一类，这样对k个不同的样本就构造了k个分类器，每个分类器都会有一个输出结果，选择输出最大者作为分类结果；

2)一对一分类器.k个不同的样本构造出k(k－1)/2个分类器，然后分别对这些分类器进行投票，最后得票最多的就是分类结果；

3)一对一淘汰分类器.k个不同的样本构造出k(k－1)/2个分类器，对这些分类器进行优先级的排序，然后根据判别函数算出优先级最高的分类器的分类结果，把含有和判别结果相反的所有分类器都淘汰，然后计算剩余中优先级最高的分类器，以此类推，最终可得出分类结果.

通过试验，选择第2)种方法作为分类方法.

4 工件识别实验

4.1 工件图像预处理

采用摄像头获取6种工件的图像，对获取的图像进行灰度化、二值化、二值化反操作、闭运算等预处理，如图3所示.工件从左向右依次定义为工件1，工件2，工件3，工件4，工件5，工件6.然后对处理后的图像提取其7个不变矩和组合矩，最后把提取的特征分别送到SVM分类器进行训练，形成能够识别工件的SVM分类器.

图3 工件预处理图像

4.2 试验结果

通过对所有工件图像按0.5，0.8，1.2，1.5倍率进行缩放，并每隔15度旋转一次，形成共计168张图片.分别提取所有工件7个不变矩和组合矩作为SVM的训练样本［7－9］，并且对样本进行训练.随机从168张图片中选择100张图片作为训练样本，剩余68张图片作为预测样本.图4是工件1分别旋转15度、30度、45度、60度、75度的图像，图5中从左向右依次是工件1原图、缩小0.5倍、缩小0.8倍、放大1.2倍、放大1.5倍的图像.这些旋转后和缩放后的图像在一定程度上和原图相比产生了失真.如果通过实验得到的失真之后的图像提取特征和原图提取特征之间误差较小，则可认为提取的特征具有RST不变性，实验结果如表1，表2所示.

图4 工件1部分旋转结果

图5 工件1部分缩放结果

如表1所示，提取的是6种工件的7个不变矩和组合矩数据.从7个不变矩数据可以看出，不同工件之间的不变矩数据具有良好的区分度，所以可以作为识别的特征.从最后3列组合矩的数据可知，3个组合矩之间具有更加良好的区分度，并且相对于7个不变矩而言，特征维数缩小了一倍还多，不仅减小了运算的复杂度，而且也缩减了识别时间，提高了识别率.

表2提取的是工件1在部分旋转情况下的7个不变矩和组合矩数据.从表中的数据可以看出，旋转的度数虽然变化了15度，但是7个不变矩和3个组合矩之间的误差变化却很小，由此可以得出，不变矩和组合矩特征具有良好的旋转不变性.通过类似的实验，可以得出工件进行缩放后，不变矩和组合矩特征具有良好的缩放不变性.同理可以证明它们也具有平移不变性.综上可知，提取的不变矩和组合矩特征具有RST不变性，可以作为工件识别的特征.

表1 6种工件的7阶矩和组合矩

表2 工件1部分旋转情况下的7阶矩和组合矩

选择SVM作为分类器，就需要考虑核函数的问题.表3列出了不同核函数情况下的识别率，分别对比了多项式核函数、RBF核函数、两层感知器核函数在提取组合矩特征情况下的识别率.从结果可以看出，对68张测试样本，RBF对应的核函数识别出了66张，在3类核函数中识别率最高，所以最终选择了RBF作为分类器的核函数.

以Matlab2012a作为软件环境，提取工件的7个不变矩和组合矩作为识别特征，采用SVM作为分类器，对工件的识别结果进行了仿真.对SVM分类器的相关参数进行了设定，其中设定核函数为RBF核函数，－g为0.0000000005，－c为10000000，采用一对一的分类方法，用SVM分别在不变矩和组合矩情况下提取的特征进行识别，最后得到7个不变矩阶矩的识别率为82.3%，组合矩的识别率高达94.1%(表4).由此可知，此处提出的组合矩在工件的识别和分类中具有较明显的分类优势.

表3 不同核函数情况下的识别率

表4 实验结果

5 结束语

提取Hu不变矩和组合矩作为工件的识别特征，利用SVM作为分类器分别对提取的两类特征进行分类.分析实验结果可知，用组合矩代替Hu不变矩作为工件的特征进行识别，不仅降低了工件识别的特征维数，减少了运算复杂度，而且提高了识别率.

从实验结果可以看到，尽管利用组合矩作为特征的识别率达到了94.1%，但是68个测试样本中还存在4个样本没有识别出来，经过进一步的相关实验得出工件没有完全得到识别的原因主要是实验中的样本都是多次使用的工件，表面形成了缺陷区域，使得工件之间特别是相似的工件之间，在进行预处理之后，提取的组合矩特征不能精确标识工件的特征，影响了工件的分类精度.在以后的研究中，还要继续优化工件提取的特征，进一步提高工件的识别率.

［1］HU M K.Visual Pattern Recognition by Moment Invariants［J］.IEEE Transactions Theory，1962，8(2)：179－187

［2］杨帆.数字图像处理与分析［M］.北京：北京航空航天大学，2010

［3］VAPNIK V.The Nature of Statistical Learning Theory［M］.New York：springer－verlag，1995

［4］张铮，倪红霞，苑春苗，等.精通Matlab数字图像处理与识别［M］.北京：人民邮电出版社，2013

［5］李盼池，许少华.支持向量机在模式识别中的核函数特性分析［J］.计算机工程与设计，2005，26(2)：302－304

［6］奉国和.SVM分类核函数及参数选择比较［J］.计算机工程与应用，2011，47(3)：123－124

［7］匡逊君，赵文倩，李明富.基于图像不变矩和SVM的机械零件分类识别［J］.制造业自动化，2012，34(8)：65－68

［8］付立思，刘朋维，李丹丹.一种改进的不变矩特征与物体识别［J］.计算机工程与应用，2012，48(31)：183－185

［9］田丽，曹安照，王蒙，等.基于SVM和神经网络组合预测模型物流需求预测［J］.重庆工商大学学报：自然科学版，2012，29(9)：61－64

Research on the Application of SVM and Combined Moment in Mechanical Parts Recognition

ZHOU Wei－feng，JIANG Juan-juan，LIN Yuan-sheng，XU Gang

(Anhui Provincial Lab of Detection Technology and Energy Saving Devices，Anhui Polytechnic University，Wuhu 241000，China)

To solve the problem of mechanical parts recognition in the factory，a method of applying Support Vector Machine and combined moment to recognize mechanical parts is proposed.By extracting the Hu invariant moment of the image，combining the first and second moments into φ12，combining the third and fourth moments into φ34，combining the fifth and sixth moments into φ56，and ignoring the seventh momentφ7，the new method is constructed.The improved algorithm reduces feature dimension and recognition time，and at the same time improves recognition accuracy.The experiment comparing classification effect of the two methods shows that the recognition rate of the method extracting Hu invariant moments as features is 82.3%，while the recognition rate based on the combined moment as features is 94.1%which is higher than the former.

SVM；Hu invariant moments；combined moment；artifacts taxonomy

TP18

A

1672－058X(2015)04－0078－07

10.16055/j.issn.1672－058X.2015.0004.018

2014－10－11；

2014－10－29.

2014年安徽省教育厅自然科学研究项目(PCNN－SOFM神经网络在工业机器人目标识别中的应用)；2013年安徽工程大学优秀青年人才基金项目(2013RZR009).

周伟峰(1990－)，男，安徽亳州人，硕士生，从事控制科学与工程的研究.